Презентация "Чтение графиков. ЕГЭ" по математике – проект, доклад
Презентацию на тему "Чтение графиков. ЕГЭ" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...«Примеры преобразования графиков функций»
у = х3 у = -х3 у = (х - 1)3 у = х3 + 1 у = 2х3 у = (2х)3 х = у3. у = х4 у = -х4 у = (-х)4 у = (х-1)4 у = х4-1 у = -2х4 x = y4. у = 3х у = 3-х у = ...Уравнения в ЕГЭ по математике: примеры и решения
ТИП ЗАДАНИЯ: Уравнение. ХАРАКТЕРИСТИКА ЗАДАНИЯ: Несложное показательное, логарифмическое, тригонометрическое или иррациональное уравнение. КОММЕНТАРИЙ: ...Система подготовки к ГИА и ЕГЭ с начальной школы
План действий:. Изучить демо-версии, спецификации и кодификаторы к работам по математике. Изучить требования к планируемым результатам начального ...Решение заданий ЕГЭ математика В6
В А С катет гипотенуза. . Теорема Пифагора: Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Основное тригонометрическое ...Преобразование тригонометрических графиков
Характеристика преобразований графиков функций у=mf(x), y=f(kx) из графика функции y=f(x). 1. Если известен график функции y=f(x), то график функции ...Преобразование графиков тригонометрических функций
Цели урока:. Обобщить и систематизировать знания учащихся по теме. Показать актуальность темы в связи с введением ЕГЭ в штатный режим. Показать возможности ...Построение графиков функций, содержащих переменную под знаком модуля
1. Построение графиков функций вида y=|f(x)|. По определению модуля, выражение y=|f(x)| равносильно системе f(x), если f(х)0, Y= -f(x), если f(x). ...Взаимное расположение графиков линейных функций
Проверка домашней работы. № 324. у=2х 4 2. № 329 (б). у = 5х А (6; -2); -2 = 5 · 6; -2 ≠ 30; А не принадлежит графику функции В (-2; -10); -10 = 5 ...Взаимное расположение графиков линейной функции
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Варианты заданий ЕГЭ по математике
Структура работы по математике. На выполнение экзаменационной работы по математике дается 4 часа (240 минут). В работе 30 заданий. Они распределены ...Асимптоты. Построение эскизов графиков
Определение: прямая вида x=a называется вертикальной асимптотой для y=f(x), если. 1. Определение: прямая вида y=b называется горизонтальной асимптотой, ...Алгоритмы построения графиков функции
График функции у = |х| а) Если х≥0, то |х| = х функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х. Построить ...«Решение задания С1 ЕГЭ по информатике и ИКТ»
2 балла. Решение задания С1 ЕГЭ по информатике и ИКТ. Кунина В.В. область I область II. 0 x y y = x+2 y2 + x2 = 25 y2 + x2 25 y 0 x 0 область ...Построение графиков тригонометрических функций
формирование знаний и умений преобразовать графики тригонометрических функций. Цель:. Закрепить применение программы MS Excel для построения графиков ...Построение графиков функций и уравнений, содержащих переменную под знаком модуля
Тема урока: «Построение графиков функций и уравнений, содержащих переменную под знаком модуля». Тип урока:. «Урок обобщения и систематизации знаний». ...Взаимное расположение графиков линейных функций
Какие функции вам известны? Какой формулой задается каждая из этих функций? Как называется переменная x и y в формуле, задающий функцию? Что является ...Преобразование графиков
Содержание. Параллельный перенос вдоль оси OY Параллельный перенос вдоль оси ОХ Растяжение (сжатие) в k раз вдоль оси OY Растяжение (сжатие) в k раз ...Взаимное расположение графиков линейных функций
Веселый тест. Интеллектуальная разминка. 1. Какие числа употребляются при счете а)природные; б)натуральные; в)искусственные; 2. Как называют верхний ...Преобразование графиков функций
Основные правила преобразования графиков функций. 1. У = - f(x) ← y = f(x) , отображением относительно оси ОХ. 2. У = f(- x) ← y = f(x), отображением ...Конспекты
Свойства функций. Чтение графиков функций
Муниципальное бюджетное образовательное учреждение «Усть – Вельская СОШ № 23». Свойства функций. Чтение графиков функций. Конспект урока по алгебре. ...Чтение графиков
Тема урока: Чтение графиков. Методика: педагогическая мастерская. Цель урока: закрепить построение столбчатых диаграмм, научить учащихся строить ...Чтение и запись чисел
Муниципальное бюджетное образовательное учреждение. средняя общеобразовательная школа № 49. г. Шахты Ростовской области. Урок математики в ...Свойства логарифмов. Решение заданий ЕГЭ
Тема урока: Свойства логарифмов. Решение заданий ЕГЭ. Тип урока:. закрепление полученных знаний. Це. ли урока. Образовательные:. Отработка ...Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций. Учитель: Мисник И.Ю., г Уссурийск. Тип урока: изучение нового материала. Цели урока:. Образовательная. ...Разрядный состав трёхзначных чисел. Чтение и запись трёхзначных чисел
Открытый урок. . Конкурс Учитель: Скачкова Вера Михайловна. Урок: МАТЕМАТИКА. Класс. : 2. УМК:. . «Гармония». Тема:. Разрядный ...Решение текстовых задач по вариантам ЕГЭ
Работа учителя математики. . первой квалификационной категории. МОУ «СОШ № 31» Тарасенко Н.И. ПЛАН. . УРОКА МАТЕМАТИКИ В 11 КЛАССЕ. ...Преобразование графиков тригонометрических функций
Тема урока : "Преобразование графиков тригонометрических функций ". . . Цели: . . -. образовательные:. обобщить и систематизировать знания ...Применение производной к исследованию функций и построению графиков
ОГБОУ СПО «Белгородский строительный колледж». Конспект урока по дисциплине. «Математика». Тема: «Применение производной к ...Двузначные числа. Чтение и запись. Закрепление
Урок математики в 1-ом классе. УМК «Гармония». «Двузначные числа. Чтение и запись. Закрепление». Цели и задачи урока:. Образовательные:. Закрепление ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 января 2019
Категория:Математика
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию



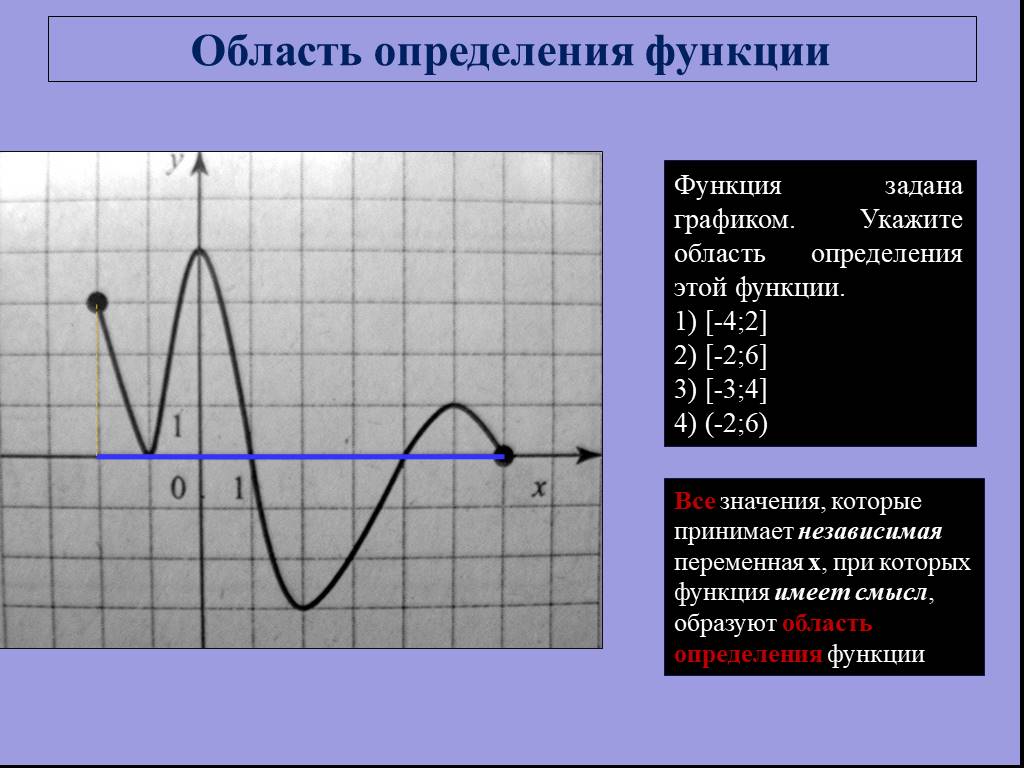
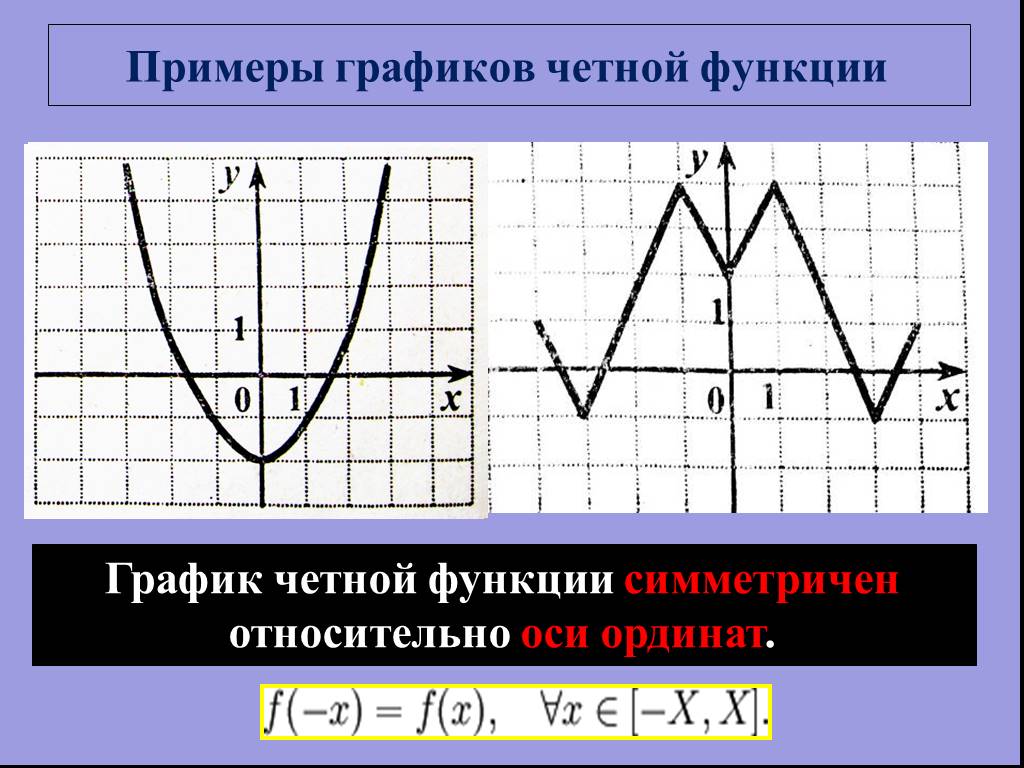

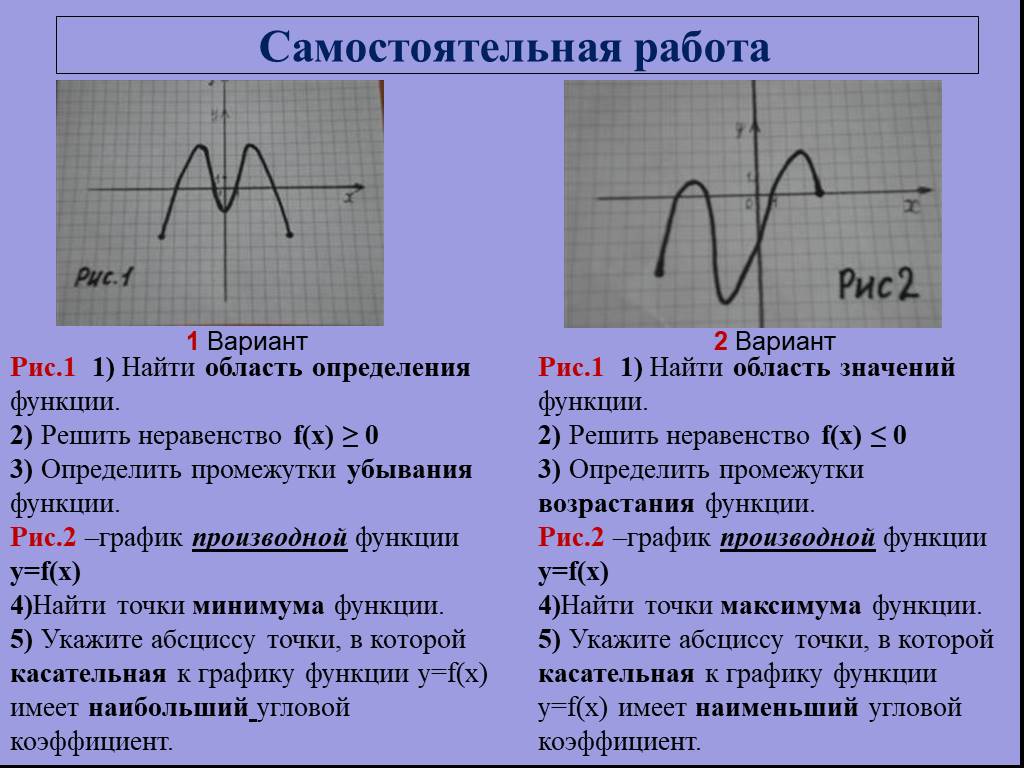




![Функция задана графиком. Укажите область определения этой функции. 1) [-4;2] 2) [-2;6] 3) [-3;4] 4) (-2;6). Область определения функции. Все значения, которые принимает независимая переменная х, при которых функция имеет смысл, образуют область определения функции Функция задана графиком. Укажите область определения этой функции. 1) [-4;2] 2) [-2;6] 3) [-3;4] 4) (-2;6). Область определения функции. Все значения, которые принимает независимая переменная х, при которых функция имеет смысл, образуют область определения функции](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen3.jpg)
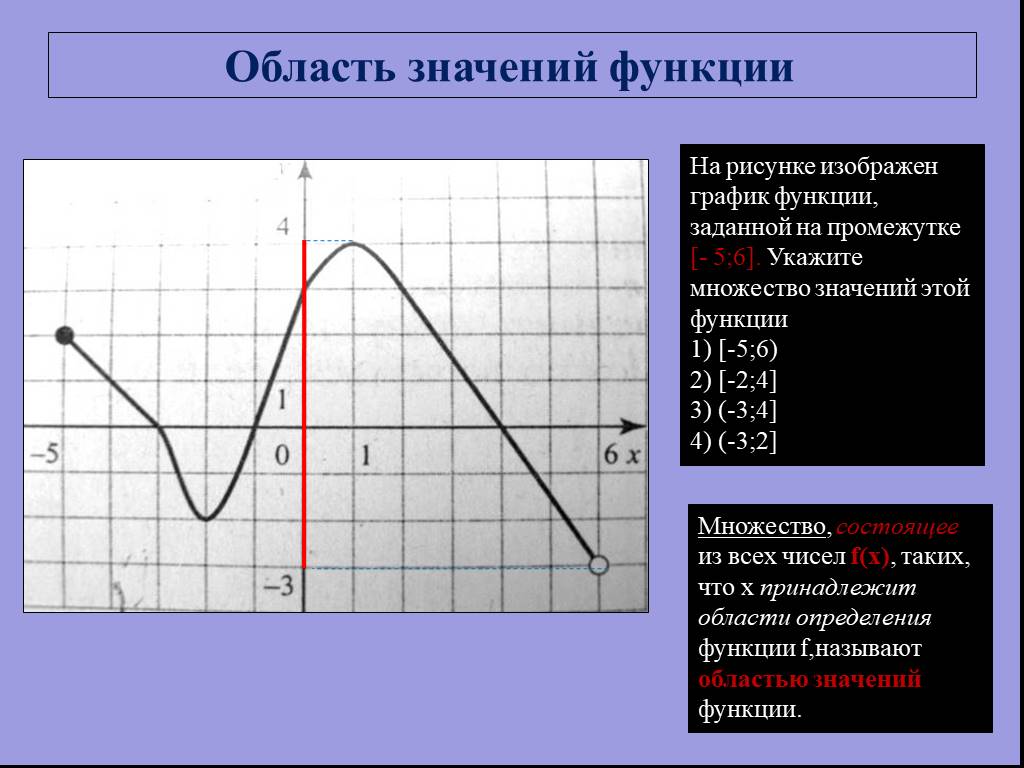
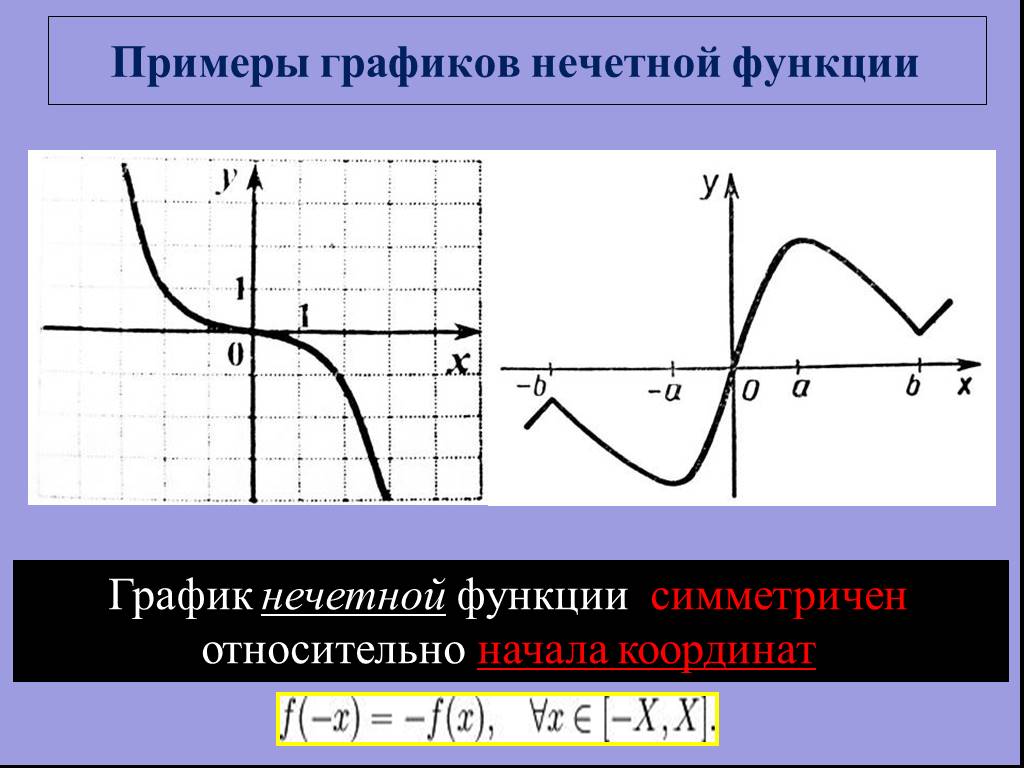
![На рисунке изображен график функции, заданной на промежутке [- 5;6]. Укажите множество значений этой функции 1) [-5;6) 2) [-2;4] 3) (-3;4] 4) (-3;2]. Область значений функции. Множество, состоящее из всех чисел f(x), таких, что х принадлежит области определения функции f,называют областью значений ф На рисунке изображен график функции, заданной на промежутке [- 5;6]. Укажите множество значений этой функции 1) [-5;6) 2) [-2;4] 3) (-3;4] 4) (-3;2]. Область значений функции. Множество, состоящее из всех чисел f(x), таких, что х принадлежит области определения функции f,называют областью значений ф](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen4.jpg)
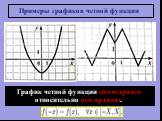
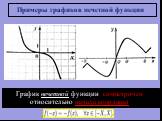
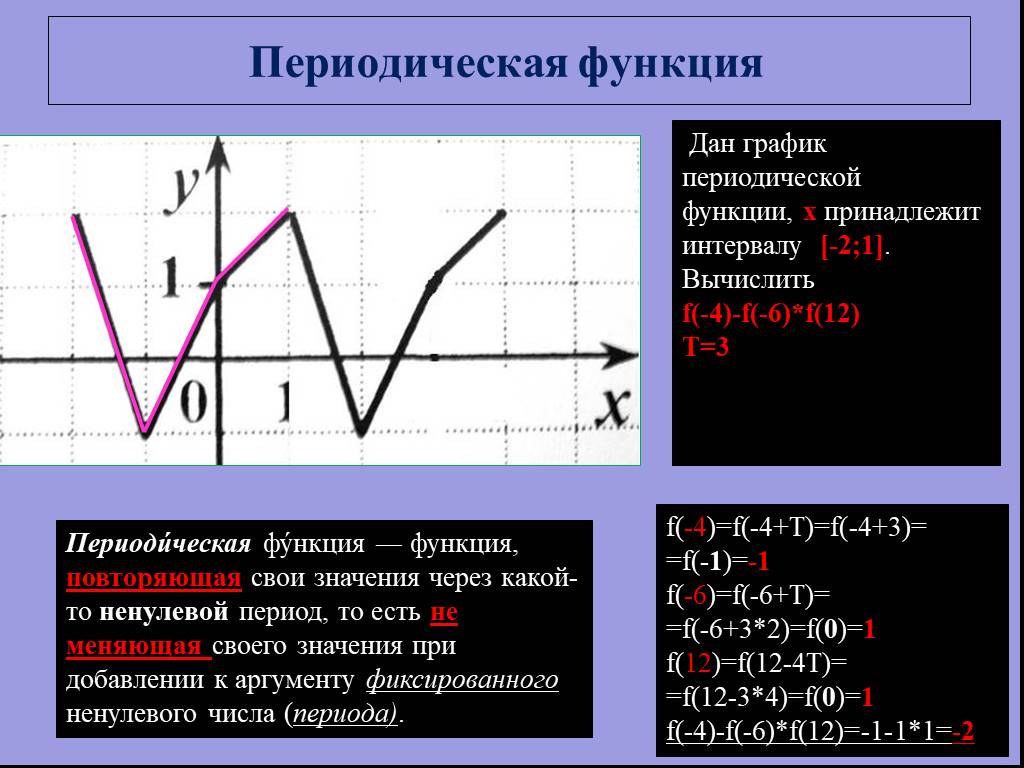
![Периодическая функция. Периоди́ческая фу́нкция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода). Дан график периодической функции, x принадлежит интервалу [-2;1]. Вычислить f Периодическая функция. Периоди́ческая фу́нкция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода). Дан график периодической функции, x принадлежит интервалу [-2;1]. Вычислить f](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen7.jpg)
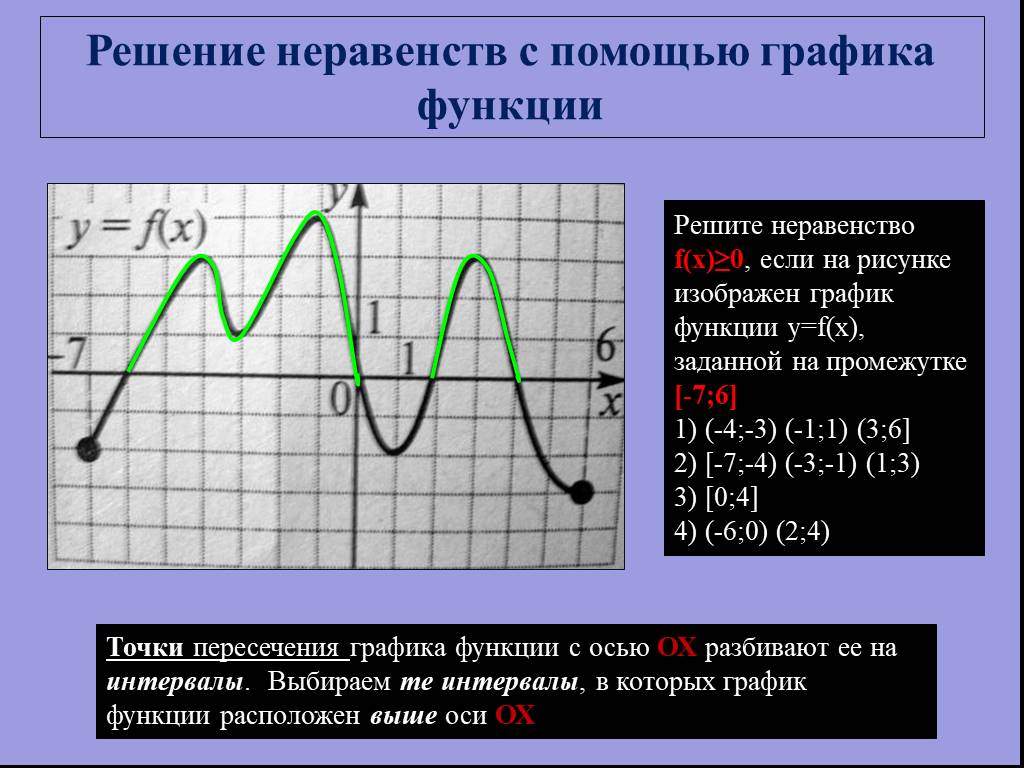
![Решите неравенство f(x)≥0, если на рисунке изображен график функции y=f(x), заданной на промежутке [-7;6] 1) (-4;-3) (-1;1) (3;6] 2) [-7;-4) (-3;-1) (1;3) 3) [0;4] 4) (-6;0) (2;4). Решение неравенств с помощью графика функции. Точки пересечения графика функции с осью ОХ разбивают ее на интервалы. Вы Решите неравенство f(x)≥0, если на рисунке изображен график функции y=f(x), заданной на промежутке [-7;6] 1) (-4;-3) (-1;1) (3;6] 2) [-7;-4) (-3;-1) (1;3) 3) [0;4] 4) (-6;0) (2;4). Решение неравенств с помощью графика функции. Точки пересечения графика функции с осью ОХ разбивают ее на интервалы. Вы](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen8.jpg)
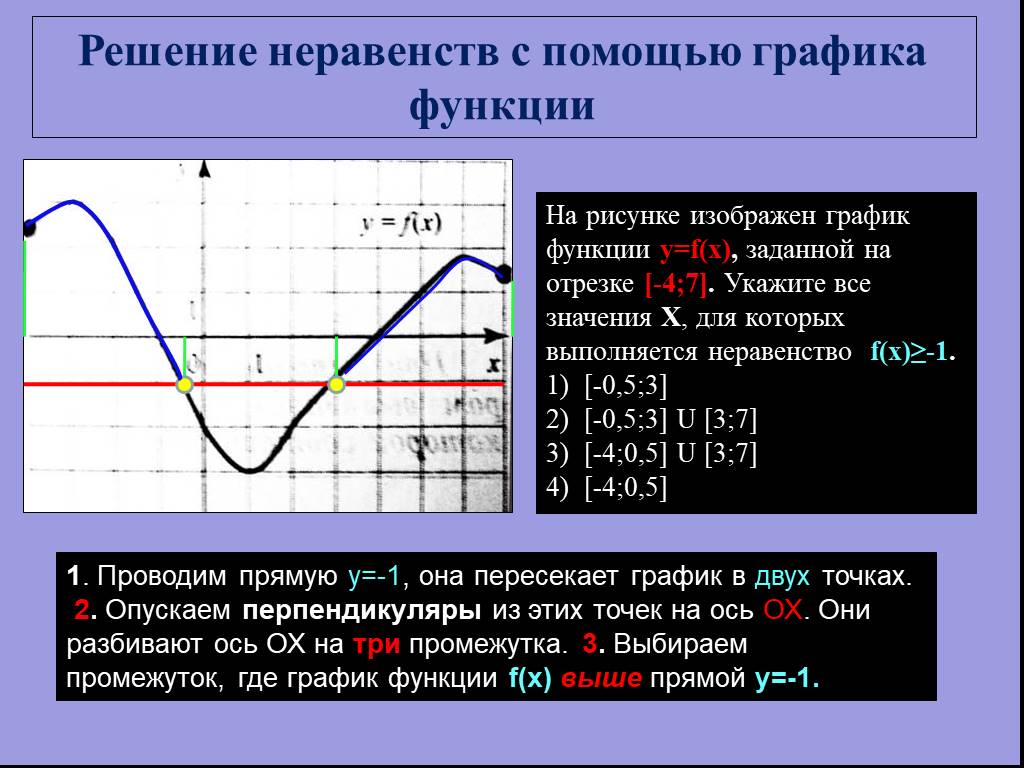
![На рисунке изображен график функции y=f(x), заданной на отрезке [-4;7]. Укажите все значения Х, для которых выполняется неравенство f(x)≥-1. [-0,5;3] [-0,5;3] U [3;7] [-4;0,5] U [3;7] [-4;0,5]. 1. Проводим прямую у=-1, она пересекает график в двух точках. 2. Опускаем перпендикуляры из этих точек на На рисунке изображен график функции y=f(x), заданной на отрезке [-4;7]. Укажите все значения Х, для которых выполняется неравенство f(x)≥-1. [-0,5;3] [-0,5;3] U [3;7] [-4;0,5] U [3;7] [-4;0,5]. 1. Проводим прямую у=-1, она пересекает график в двух точках. 2. Опускаем перпендикуляры из этих точек на](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen9.jpg)
![На рисунке изображены графики функций y=f(x),и y=g(x), заданных на промежутке [-3;6]. Укажите все значения Х, для которых выполняется неравенство f(x)≤g(x) [-1;2] [-2;3] [-3;-2] U [3;6] + [-3;-1] U [3;4]. Сравнение значений функций. 1. Находим точки пересечения графиков. 2. Опускаем перпендикуляры н На рисунке изображены графики функций y=f(x),и y=g(x), заданных на промежутке [-3;6]. Укажите все значения Х, для которых выполняется неравенство f(x)≤g(x) [-1;2] [-2;3] [-3;-2] U [3;6] + [-3;-1] U [3;4]. Сравнение значений функций. 1. Находим точки пересечения графиков. 2. Опускаем перпендикуляры н](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen10.jpg)
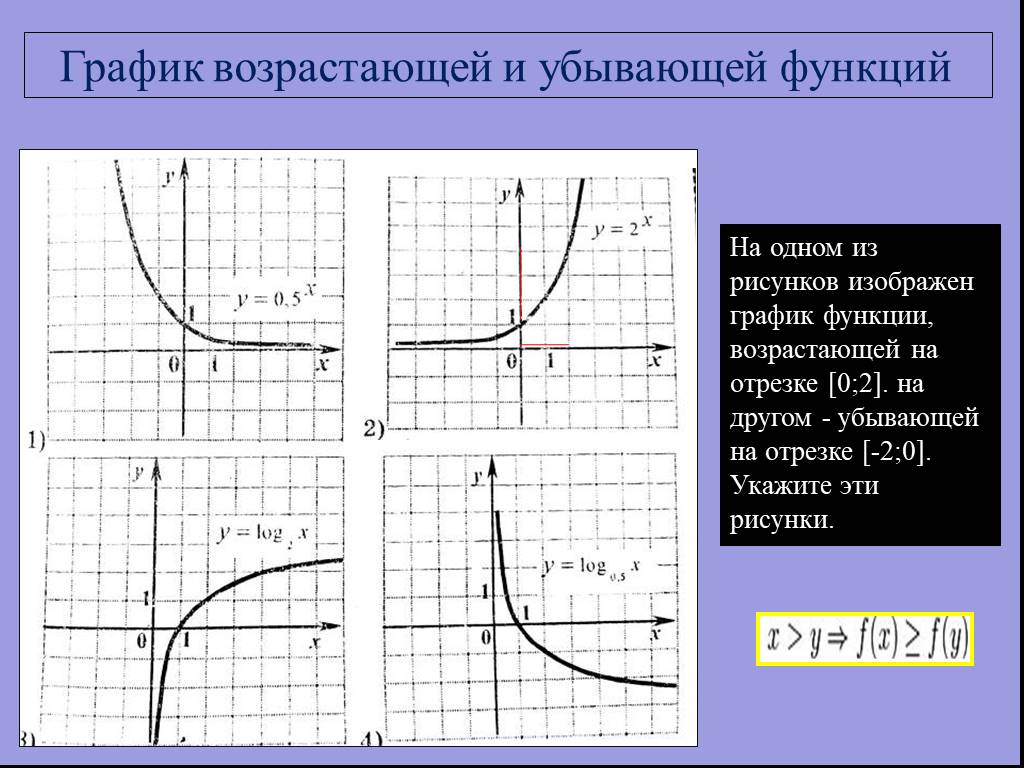
![На одном из рисунков изображен график функции, возрастающей на отрезке [0;2]. на другом - убывающей на отрезке [-2;0]. Укажите эти рисунки. График возрастающей и убывающей функций На одном из рисунков изображен график функции, возрастающей на отрезке [0;2]. на другом - убывающей на отрезке [-2;0]. Укажите эти рисунки. График возрастающей и убывающей функций](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen11.jpg)

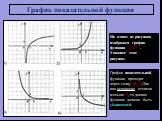

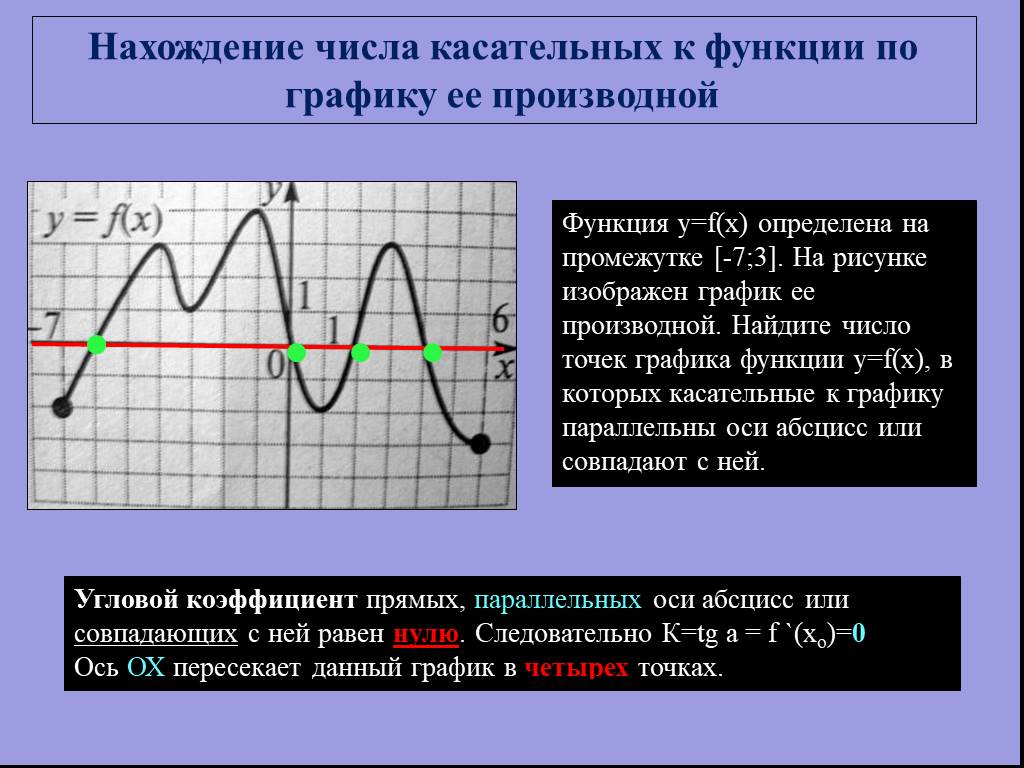
![Функция y=f(x) определена на промежутке [-7;3]. На рисунке изображен график ее производной. Найдите число точек графика функции y=f(x), в которых касательные к графику параллельны оси абсцисс или совпадают с ней. Угловой коэффициент прямых, параллельных оси абсцисс или совпадающих с ней равен нулю. Функция y=f(x) определена на промежутке [-7;3]. На рисунке изображен график ее производной. Найдите число точек графика функции y=f(x), в которых касательные к графику параллельны оси абсцисс или совпадают с ней. Угловой коэффициент прямых, параллельных оси абсцисс или совпадающих с ней равен нулю.](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen16.jpg)

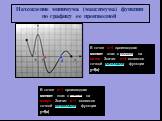
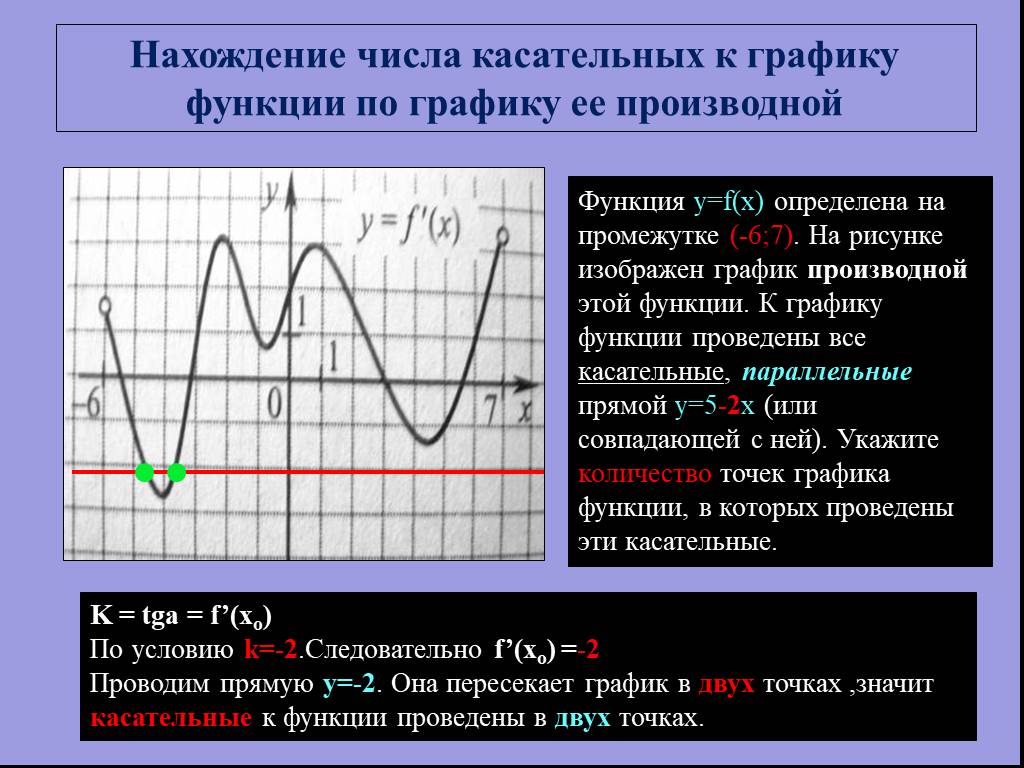
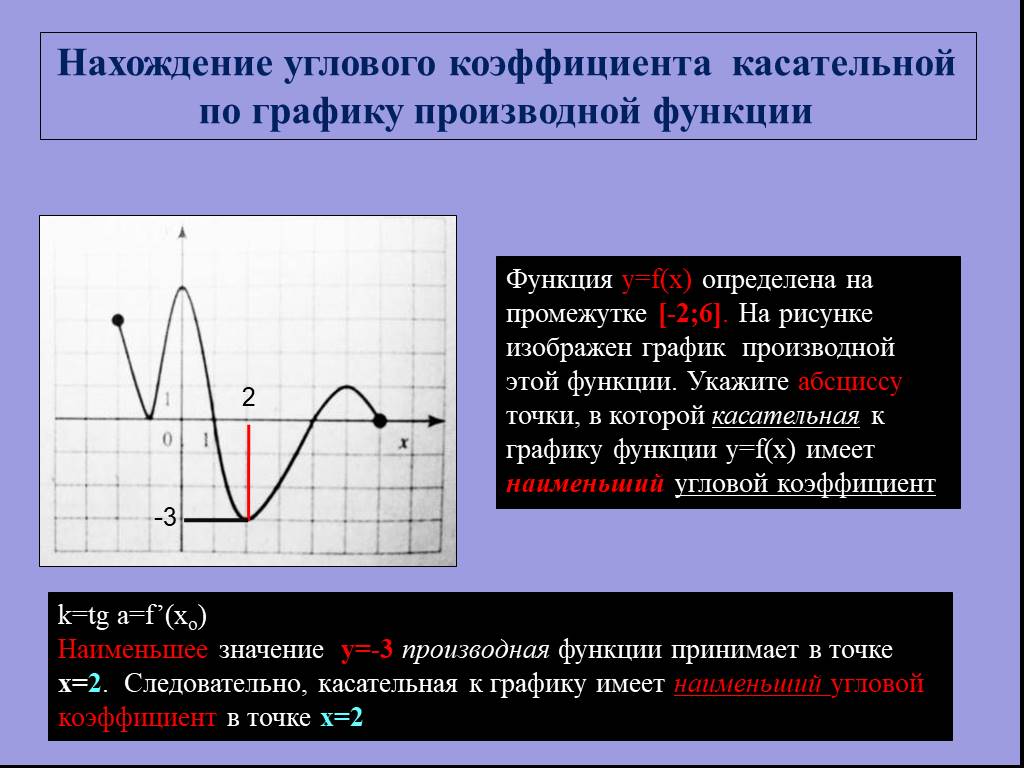
![Функция y=f(x) определена на промежутке [-2;6]. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наименьший угловой коэффициент. k=tg a=f’(xo) Наименьшее значение у=-3 производная функции принимает в точке х=2. Следова Функция y=f(x) определена на промежутке [-2;6]. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наименьший угловой коэффициент. k=tg a=f’(xo) Наименьшее значение у=-3 производная функции принимает в точке х=2. Следова](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen18.jpg)
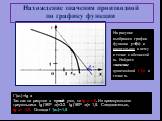
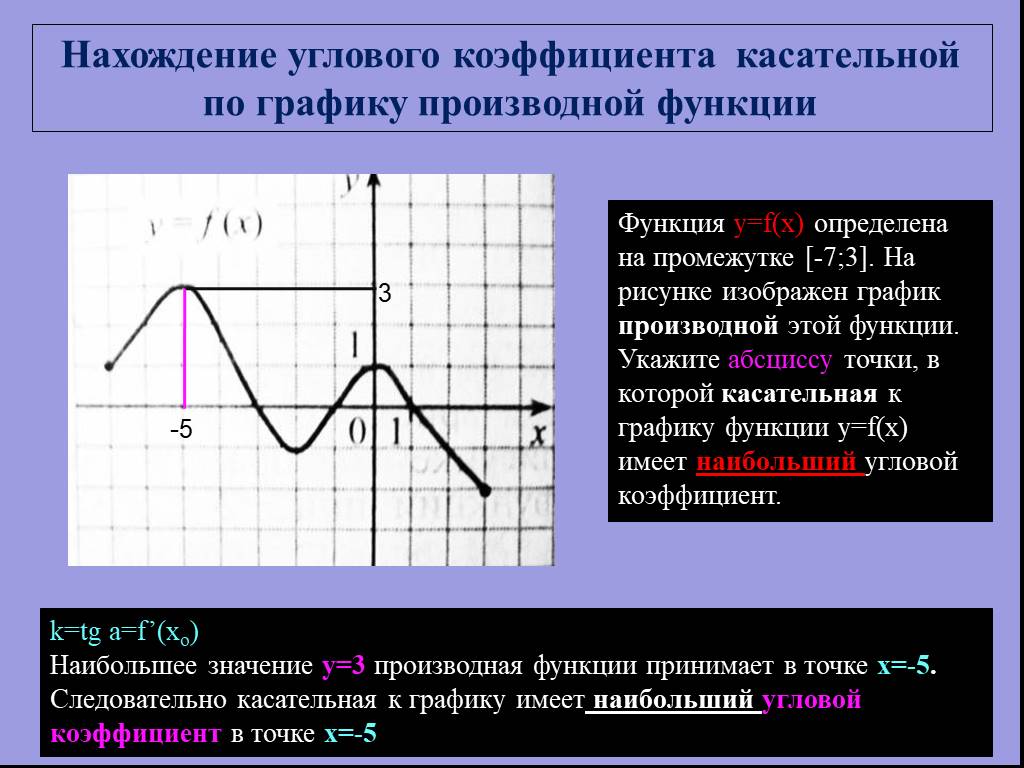
![Функция y=f(x) определена на промежутке [-7;3]. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наибольший угловой коэффициент. k=tg a=f’(xo) Наибольшее значение у=3 производная функции принимает в точке х=-5. Следова Функция y=f(x) определена на промежутке [-7;3]. На рисунке изображен график производной этой функции. Укажите абсциссу точки, в которой касательная к графику функции y=f(x) имеет наибольший угловой коэффициент. k=tg a=f’(xo) Наибольшее значение у=3 производная функции принимает в точке х=-5. Следова](https://prezentacii.org/upload/cloud/19/01/115520/images/thumbs/screen19.jpg)