Презентация "Преобразование тригонометрических графиков" по математике – проект, доклад
Презентацию на тему "Преобразование тригонометрических графиков" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Преобразование графиков тригонометрических функций
Цели урока:. Обобщить и систематизировать знания учащихся по теме. Показать актуальность темы в связи с введением ЕГЭ в штатный режим. Показать возможности ...Преобразование графиков тригонометрических функций
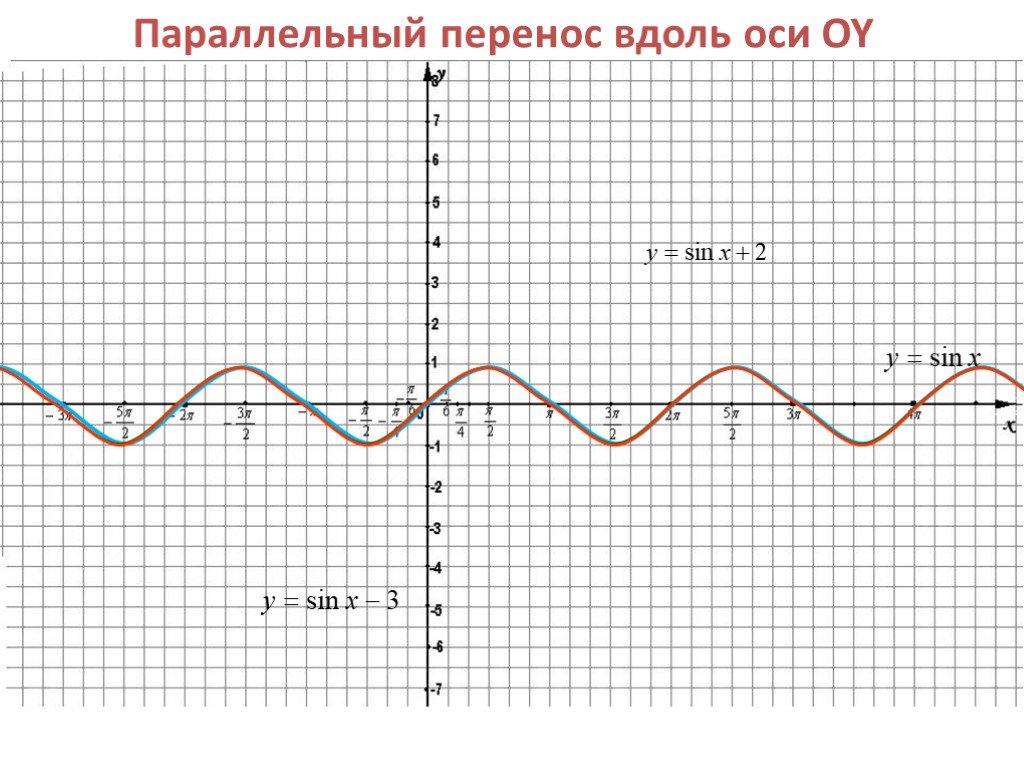
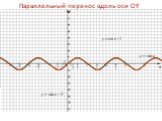
Параллельный перенос на вектор (0; b) вдоль оси ординат: График функции f(x)+b получается параллельным переносом графика f(x) в положительном направлении ...Преобразование графиков тригонометрических функций
Оборудование урока: компьютер, проектор, экран. Цели: Обобщить знания и умения. Развить умение наблюдать, сравнить, обобщать. Воспитать познавательную ...Преобразование графиков тригонометрических функций
y = cos(x+2) y=cos2x y=sinx +2 y=-3cosx y=sin1/2x y=sin(x-5) y=tg2x y=2ctgx y=ctg1/3x y=1/3sinx y=4-cosx y=ctgx+1. Сгруппируйте функции по какому-нибудь ...Преобразование графиков тригонометрических функций
Цель урока:. Повторить свойства тригонометрических функций Изучить графическую программу Advanced Grapher, облегчающую построение графиков Изучить ...Симметрия функций и преобразование их графиков
ЦЕЛИ:. Повторить определение функции; основные понятия, связанные с ней; способы задания функции. Ввести понятие чётной и нечётной функции. Освоить ...Решение задач на применение основных тригонометрических формул и преобразование выражений
Цели и задачи урока. Повторить основные тригонометрические формулы. Закрепить знания свойств синуса, косинуса, тангенса и котангенса. Научиться применять ...Преобразование графиков
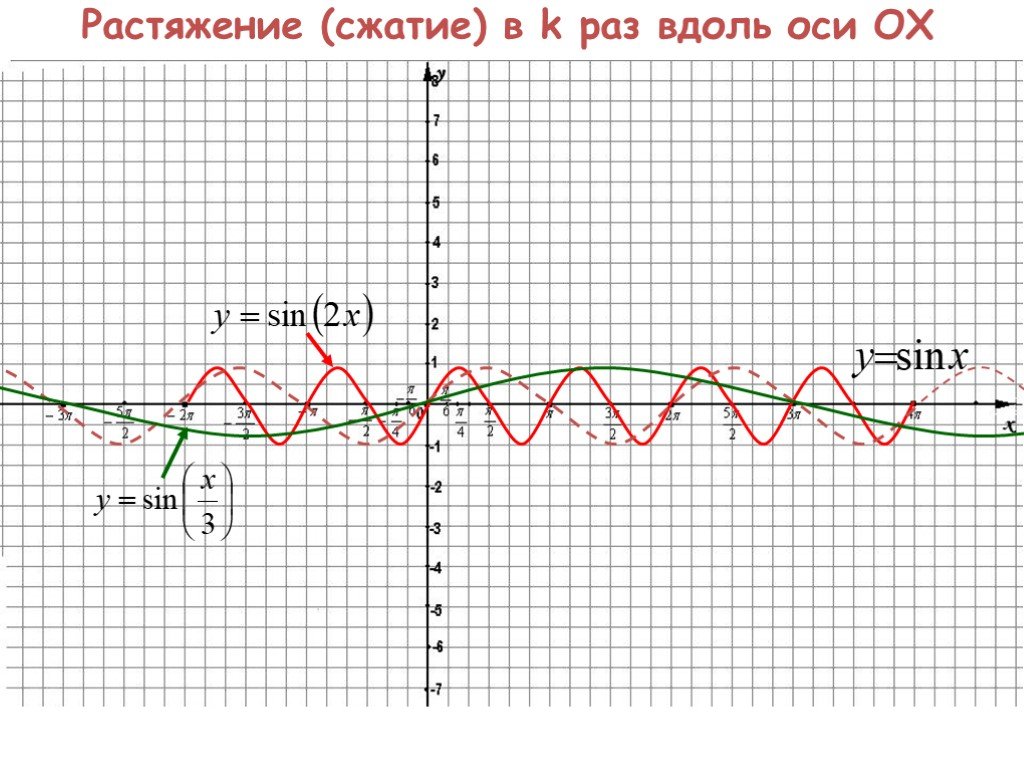
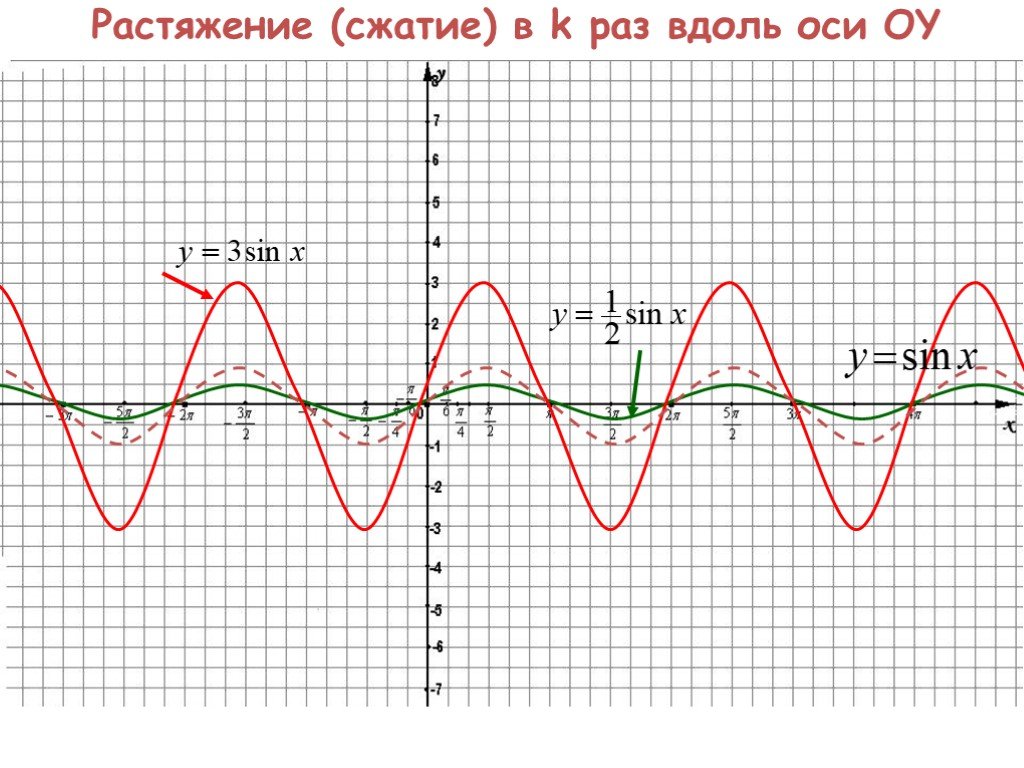
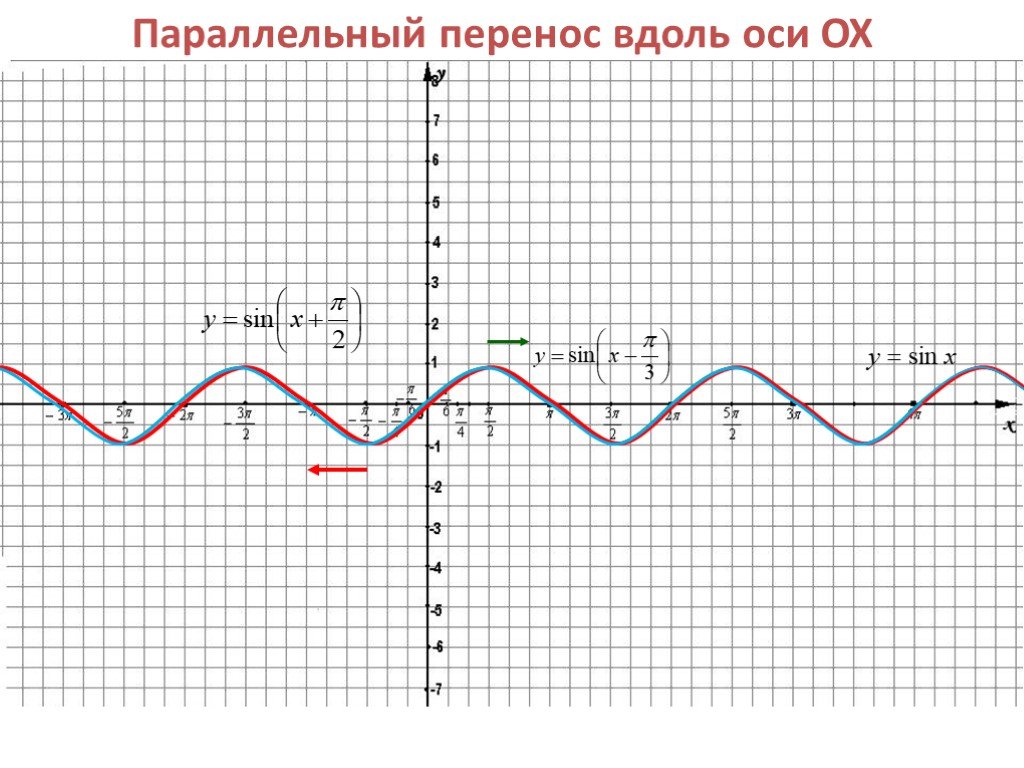
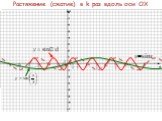
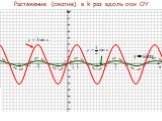
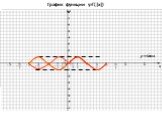
Содержание. Параллельный перенос вдоль оси OY Параллельный перенос вдоль оси ОХ Растяжение (сжатие) в k раз вдоль оси OY Растяжение (сжатие) в k раз ...Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа.
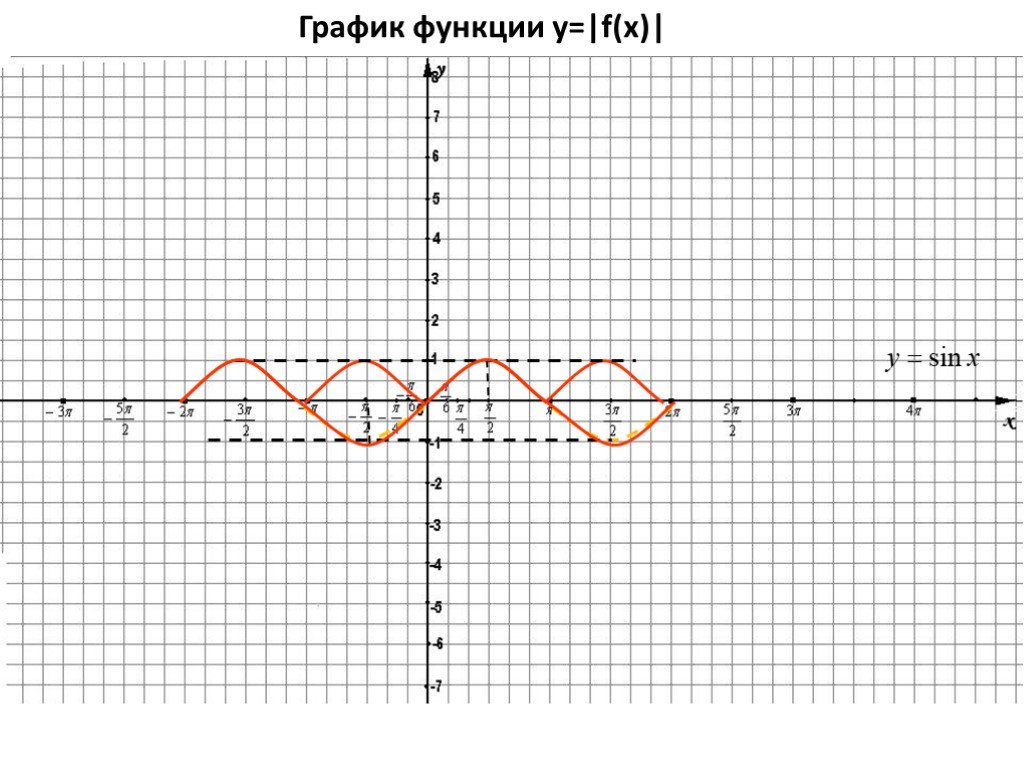
1. У = - f(x) ← y = f(x) , симметрия относительно оси ОХ. 2. У = f(- x) ← y = f(x), симметрия относительно оси ОУ. 3. У = - f (- x) ← y = f(x), симметрия ...Преобразование тригонометрических выражений
Учебные элементы. Синус, косинус, тангенс суммы и разности аргументов. Формулы двойного аргумента.(теория, примеры, задания) Формулы понижения степени. ...Преобразование графиков функций
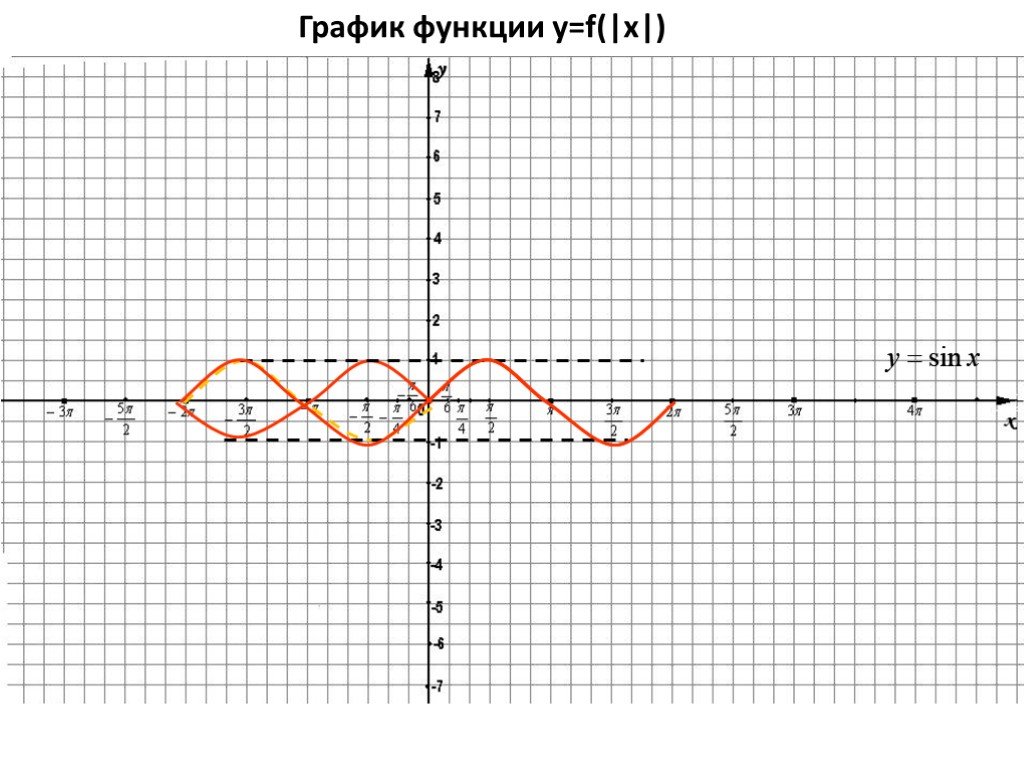
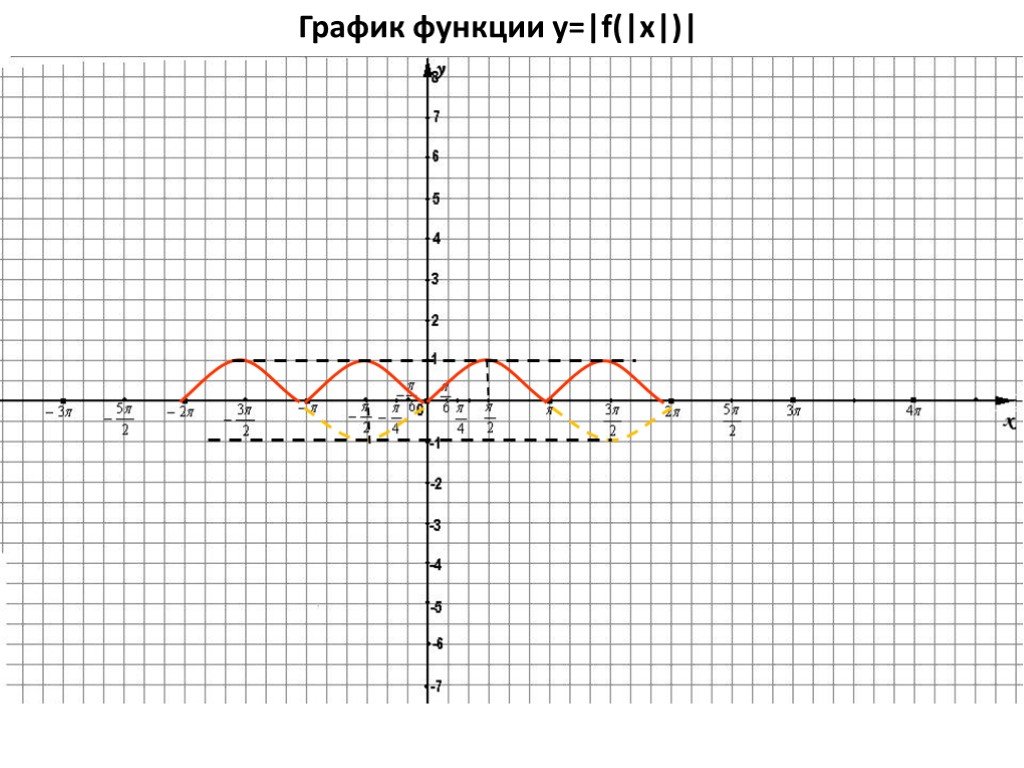
Основные правила преобразования графиков функций. 1. У = - f(x) ← y = f(x) , отображением относительно оси ОХ. 2. У = f(- x) ← y = f(x), отображением ...Преобразование графиков функций на координатной плоскости
Эпиграф к уроку. Красота в единстве теории и практики. Цели обучения, воспитания и развития. Рациональные способы построения графиков функций. Развитие ...Преобразование графиков функций
Y=f (x ). Y=f (x+c). c>0 Сдвиг по оси Ох на с единиц влево. Y= f(x+c). c. Y=f (ax). 0. Y=f(ax). a>1 Сжатие вдоль оси Ох в а раз (или к оси Оу). Y=f ...Преобразование графиков функции
Повторение. Как построить график функции если известен график функции. . Рассмотрим построение графика функции. 1 случай: m – положительное число. ...Преобразование графиков функций
Дорогу осилит идущий, а математику – мыслящий Т.Эдисон. Цель урока. Изучить способ построения графиков функций y = f(kx), y = mf(x). Преобразование: ...Преобразование графиков функций, содержащих модуль
y = f(x) + a y = f(x) y = f(x) - a +a -a. Преобразование графиков функций. Т1. Параллельный перенос по оси Оу. y = f(x) график исходной функции. y ...Построение графиков тригонометрических функций
формирование знаний и умений преобразовать графики тригонометрических функций. Цель:. Закрепить применение программы MS Excel для построения графиков ...Производные тригонометрических функций
Ввести формулы производных тригонометрических функций рассмотреть методы решения упражнений на применение изученных правил дифференцирования; вырабатывать ...Преобразования графиков функций
A B C x y 0 1. В качестве исходного графика функции y=f(x) выберем ломанную, состоящую из двух звеньев, заданных точками A(-5;-2), B(-2;4) и C(2;2). ...Преобразование целого выражения в многочлен
Цели урока:. Ввести понятие целого выражения. Закрепить знания и умения при умножении многочлена на многочлен и применение формул сокращённого умножения. ...Конспекты
Преобразование графиков тригонометрических функций
Конспект урока по алгебре в 10 классе. Васильева Екатерина Сергеевна. ,. . учитель математики. ОГБОУ «Смоленская специальная (коррекционная). ...Преобразование графиков тригонометрических функций
Тема урока : "Преобразование графиков тригонометрических функций ". . . Цели: . . -. образовательные:. обобщить и систематизировать знания ...Преобразование графиков тригонометрических функций
Математику уже затем следует учить, что она ум в порядок приводит. М. В. Ломоносов. Урок математики (продолжительность 1ч 20мин). Тема. ...Преобразование графиков тригонометрических функций
. . Воробьева Ирина Юрьевна. учитель математики. 1 категории. ГУ «Экономический лицей». г. Семей. Методическая разработка урока. ...Преобразование тригонометрических выражений
Здоровец Людмила Александровна учитель математики высшей категории. Государственное учреждение «Средняя школа №5». . . 150009, Северо-Казахстанская ...Преобразование тригонометрических выражений
учитель математики. Кулик Наталья Николаевна,. специалист высшей категории. . первого уровня. ГУ «Средняя школа № 19. отдела образования. ...Решение тригонометрических уравнений
Муниципальное бюджетное общеобразовательное учреждение. . МО г. Нягань. «Средняя общеобразовательная школа №6». РАЗРАБОТКА УРОКА ПО АЛГЕБРЕ ...Решение простейших и некоторых типов тригонометрических уравнений
План-конспект урока. . Учитель:. Дорофеева Л.И. Предмет:. математика. Класс:. 10 класс. Тема урока: «Решение простейших и некоторых типов ...Решение тригонометрических уравнений
1.Савкина Марина Петровна. 2.ГУ «Веселорощинская общеобразовательная средняя школа» Железинского района Павлодарской области. 3.Учитель математики. ...Применение основных тригонометрических тождеств к преобразованию выражений
Урок. Алгебра. 9 класс. Тема:. . «. Применение основных тригонометрических тождеств. . к преобразованию выражений». . Цели:. . Повторить ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 мая 2019
Категория:Математика
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию


























![Функция синус. Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная. Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно начала координат. Функция периодическая с наим Функция синус. Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная. Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно начала координат. Функция периодическая с наим](https://prezentacii.org/upload/cloud/19/05/146212/images/thumbs/screen17.jpg)
![Функция косинус. Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная. Функция четная: cos(−x)=cos x для всех х ∈ R. График функции симметричен относительно оси OY. Функция периодическая с наименьшим по Функция косинус. Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная. Функция четная: cos(−x)=cos x для всех х ∈ R. График функции симметричен относительно оси OY. Функция периодическая с наименьшим по](https://prezentacii.org/upload/cloud/19/05/146212/images/thumbs/screen18.jpg)