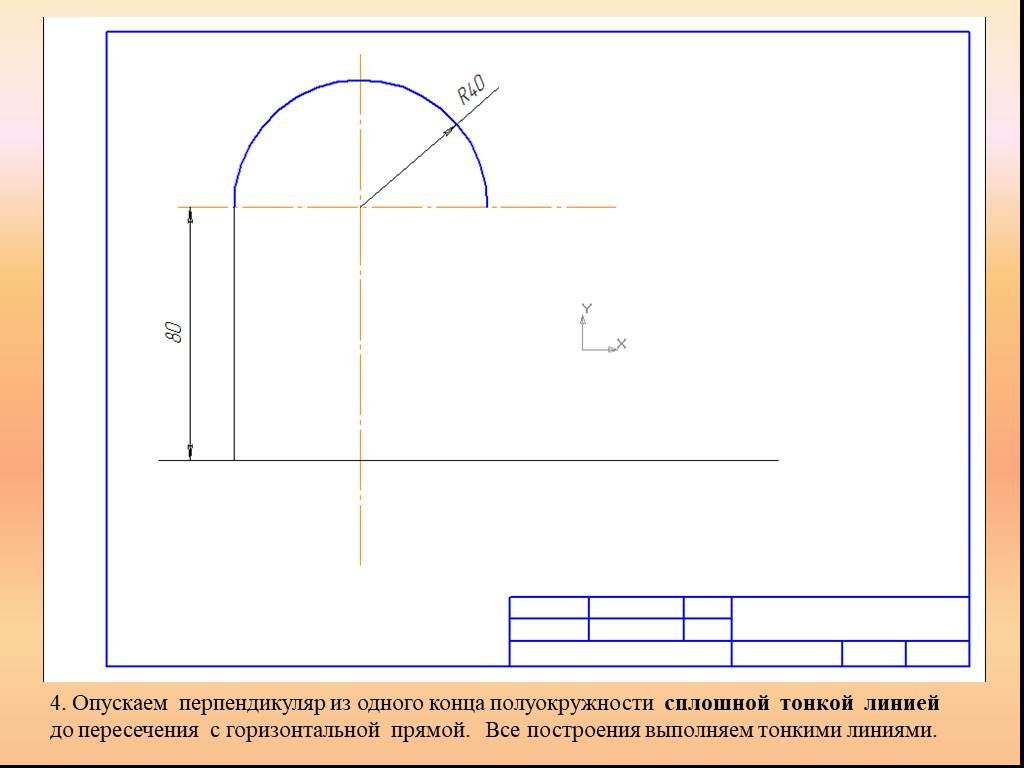
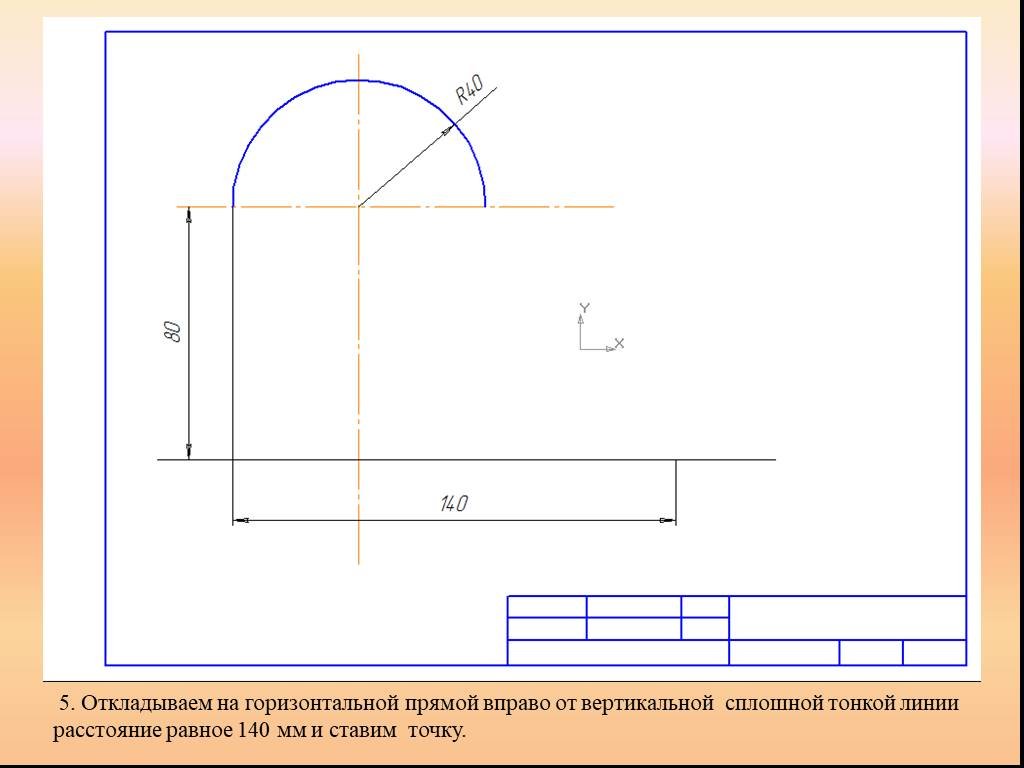
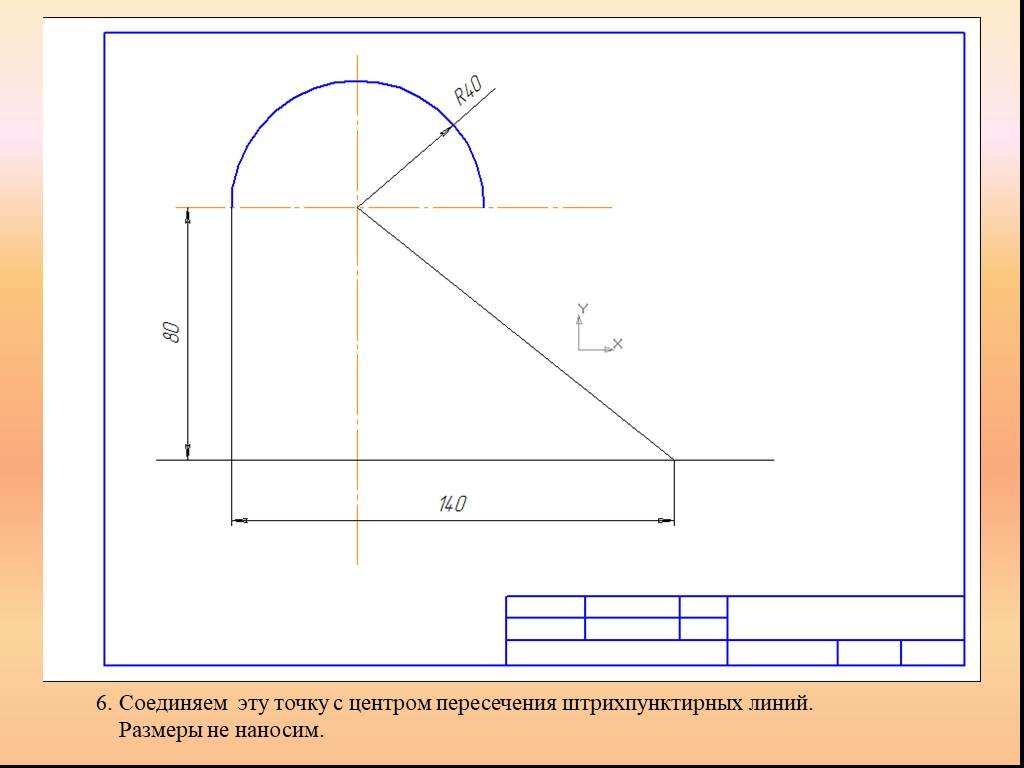
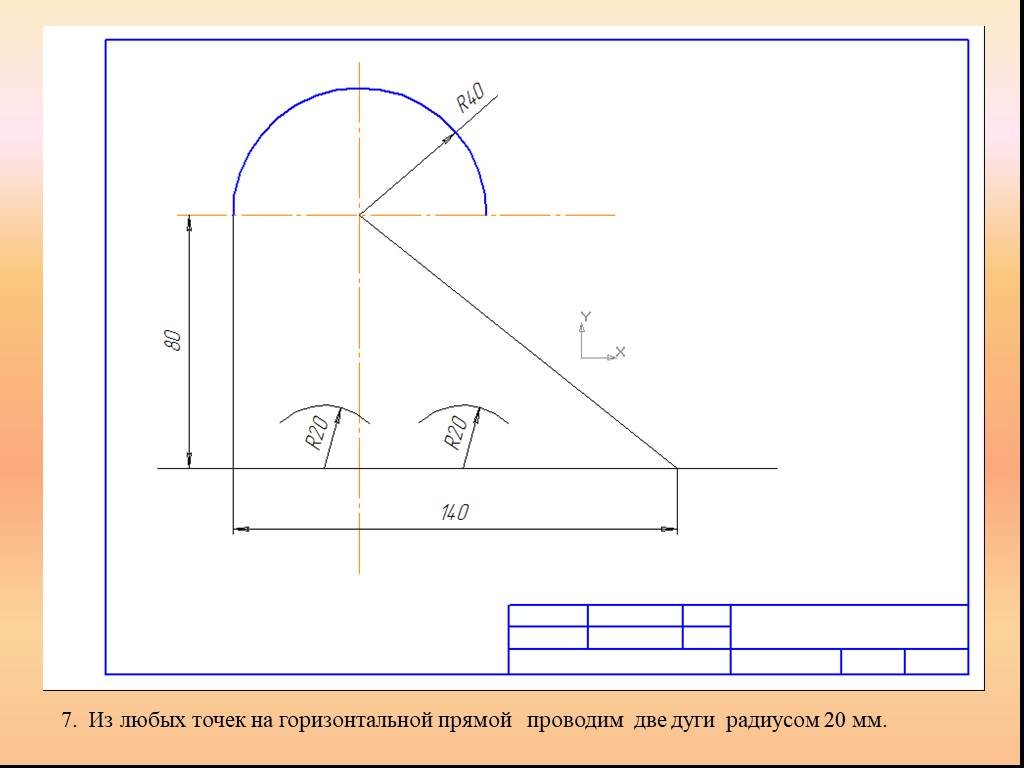
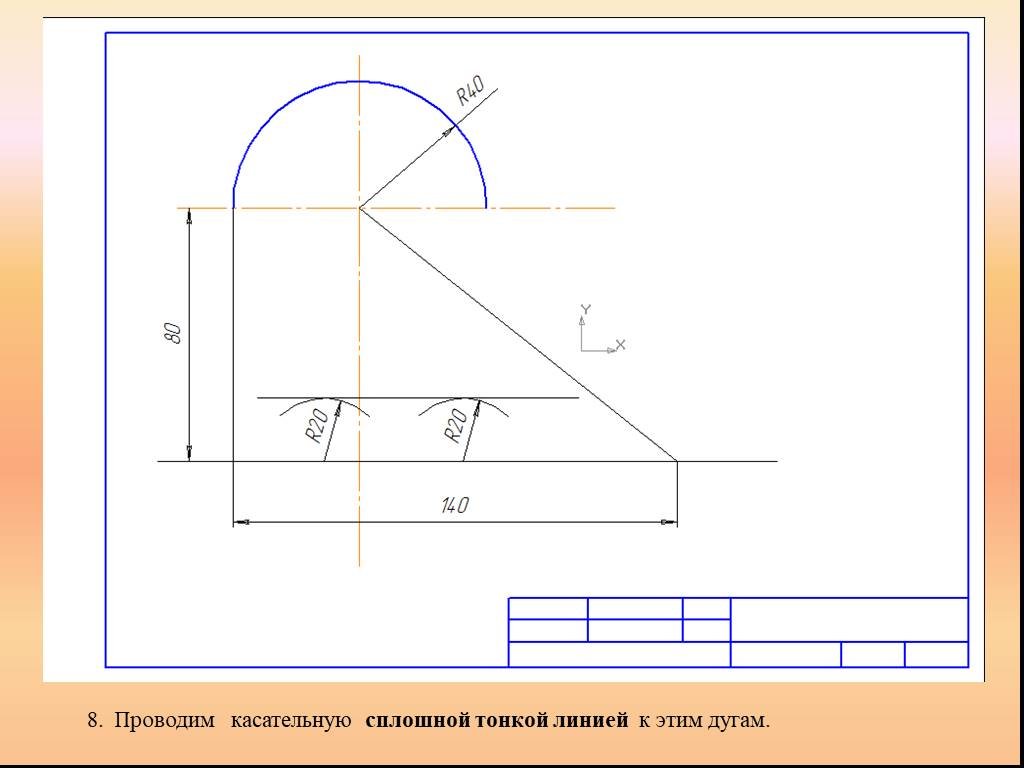
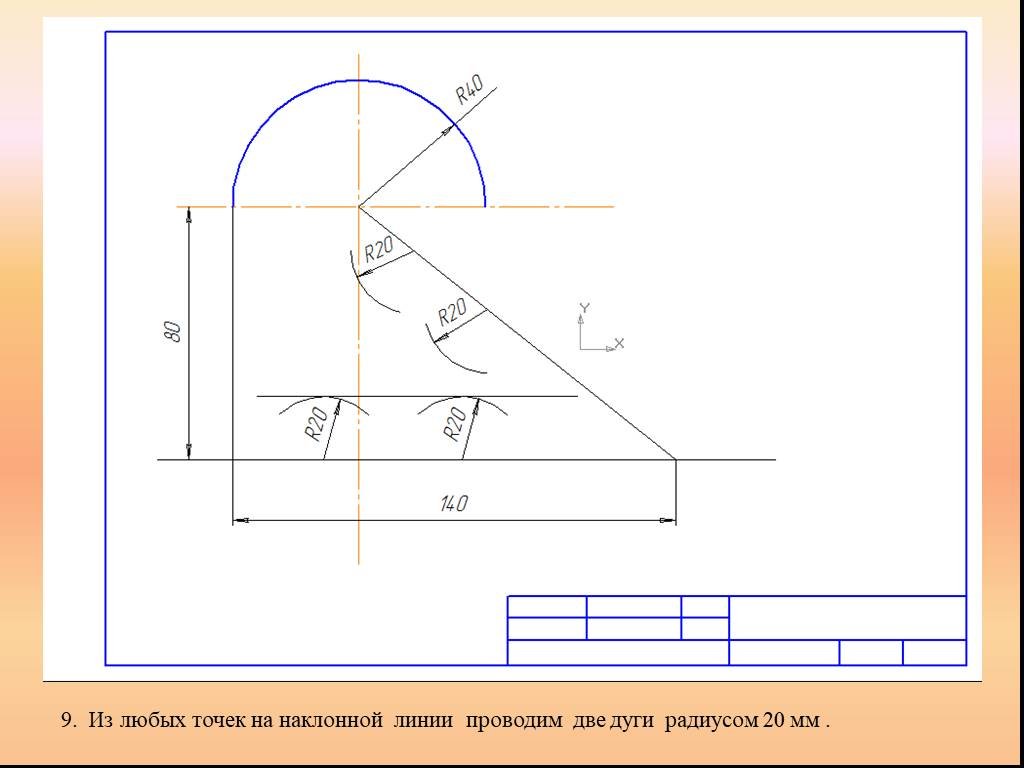
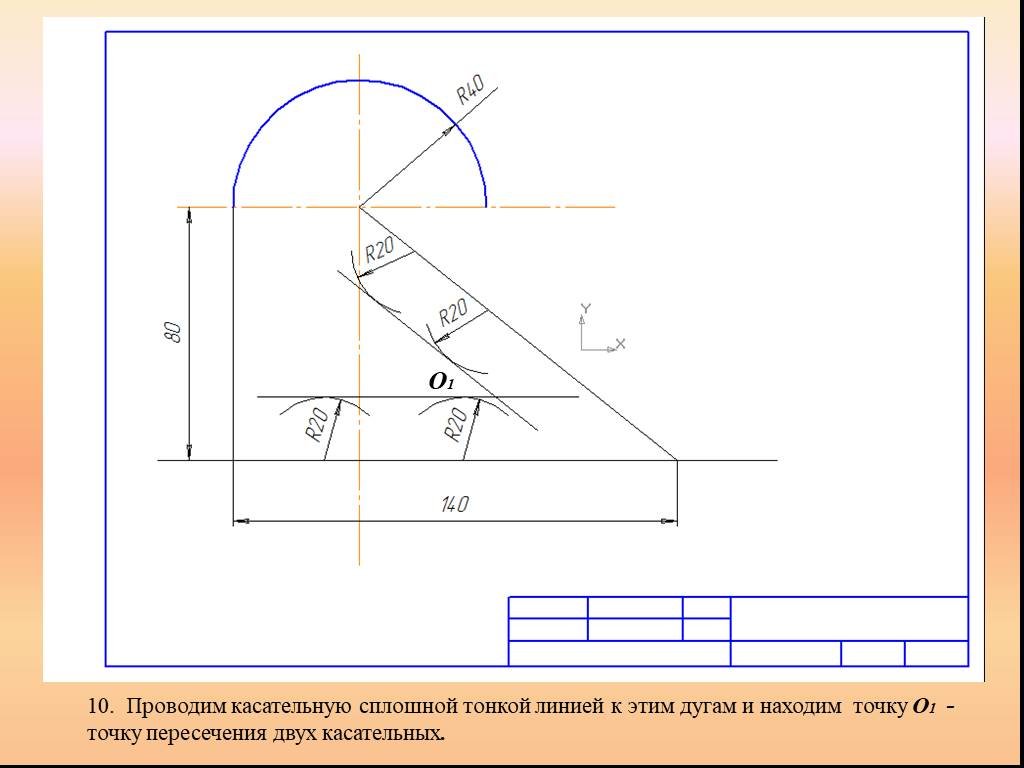
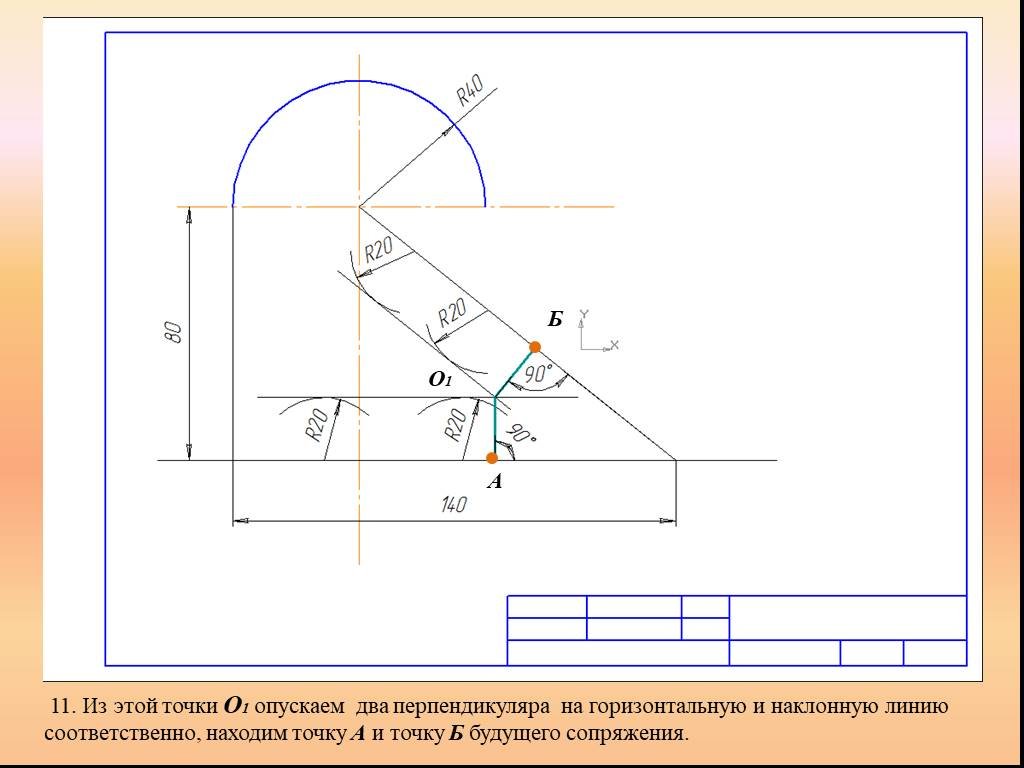
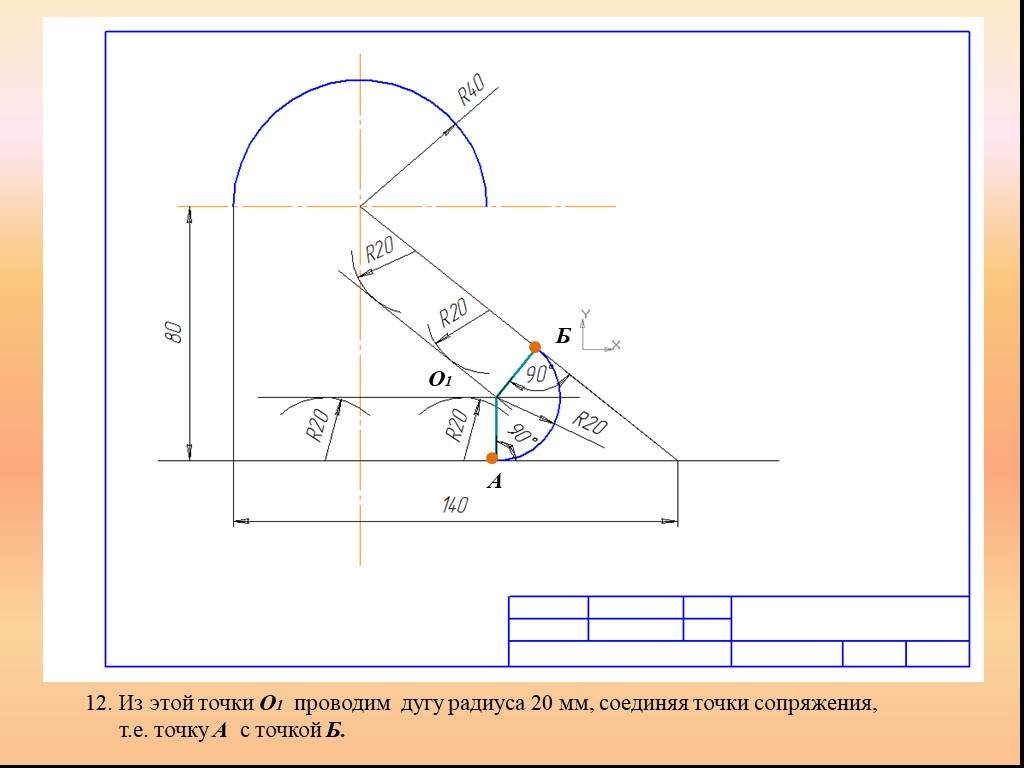
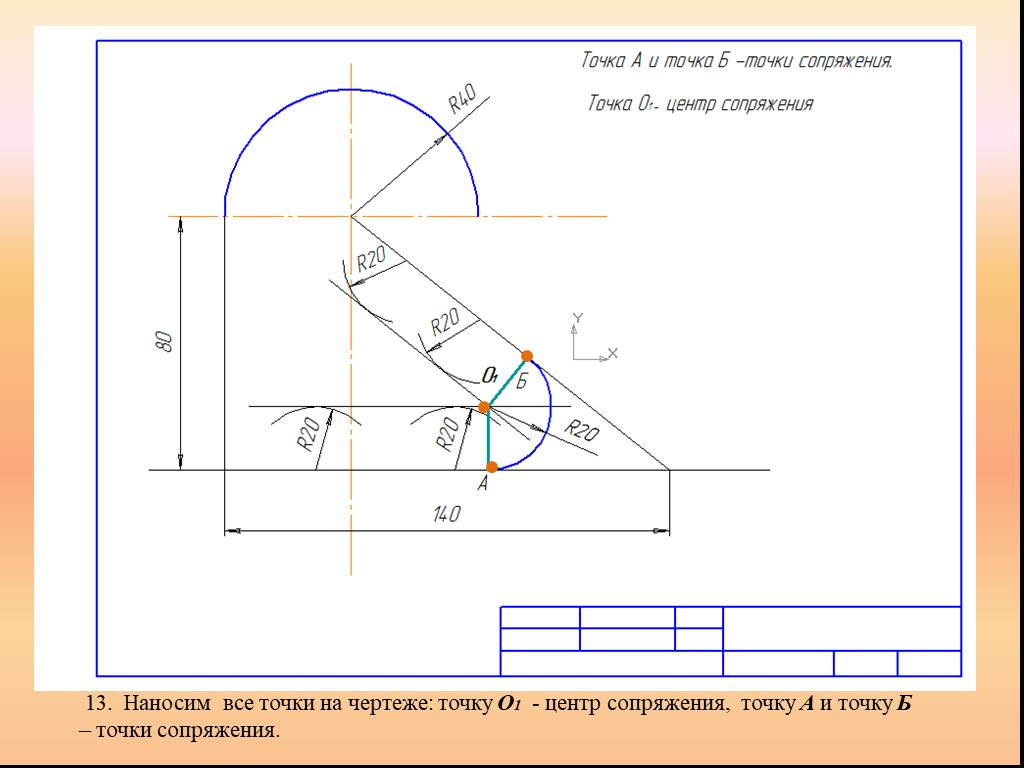
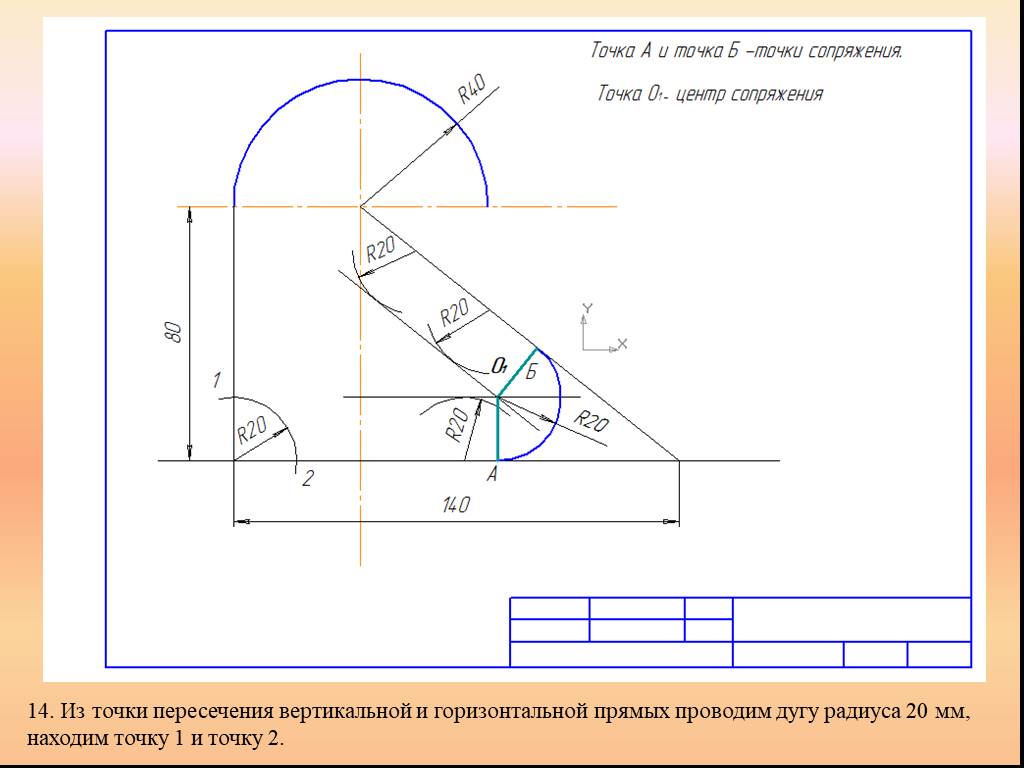
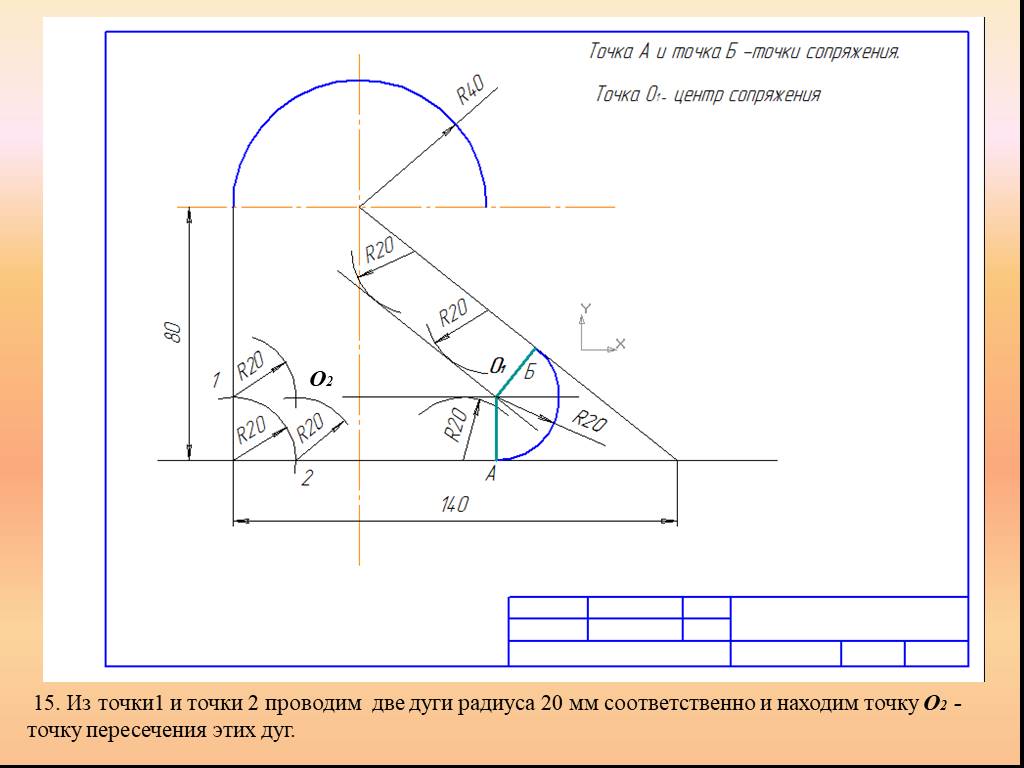
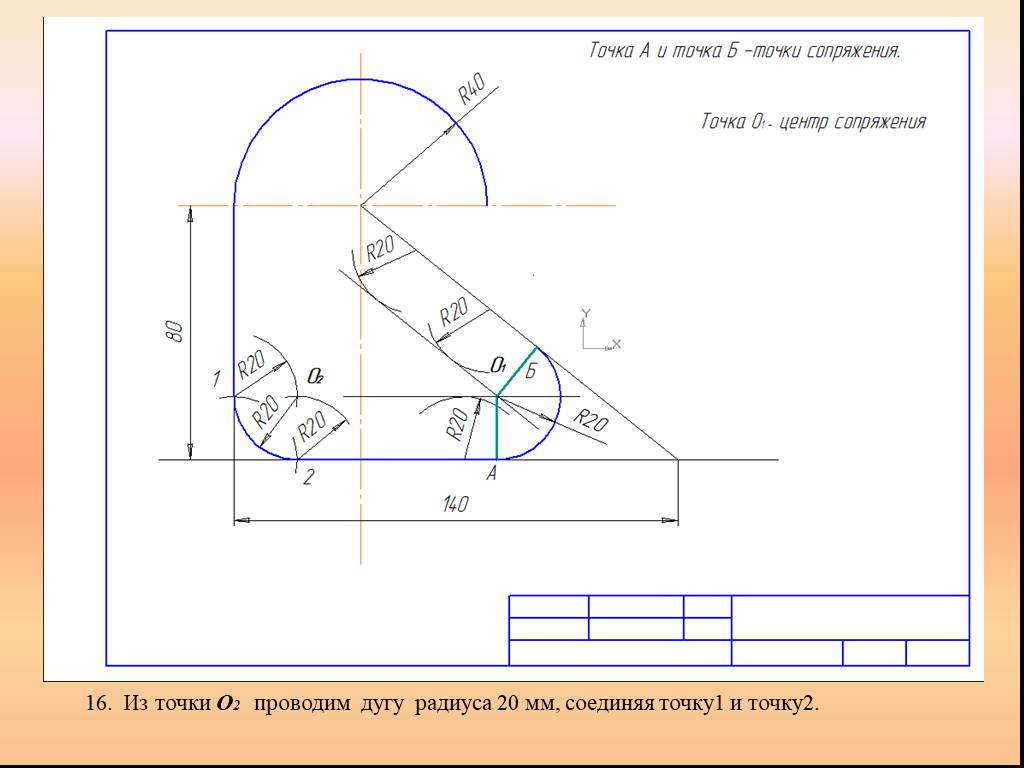
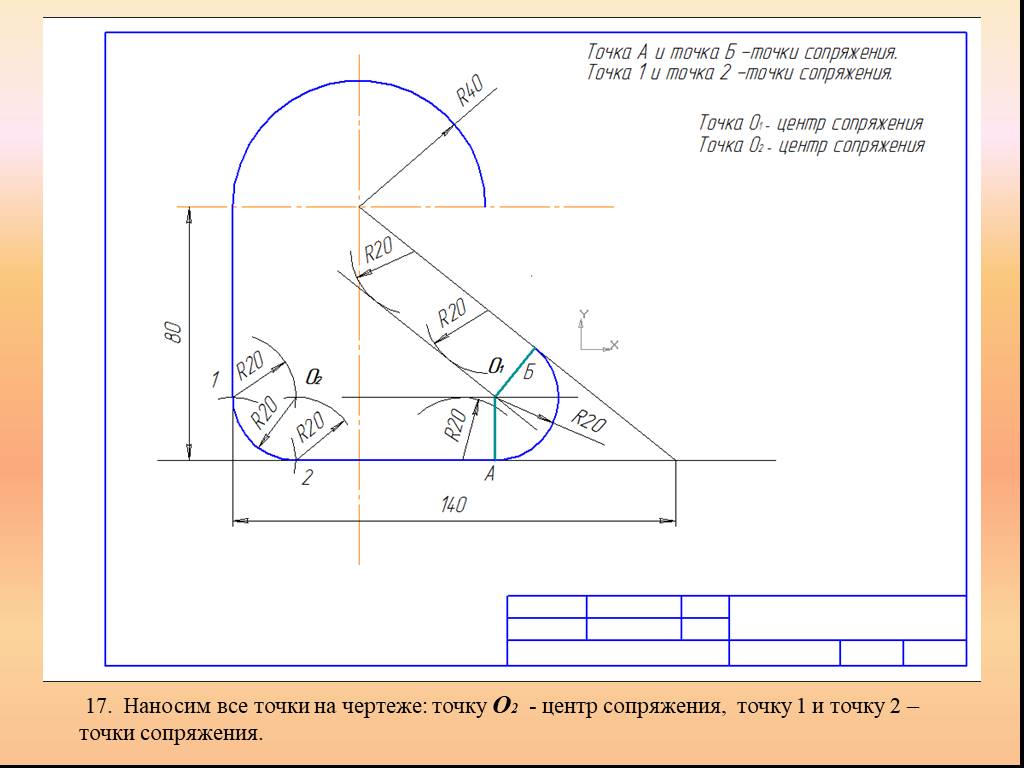
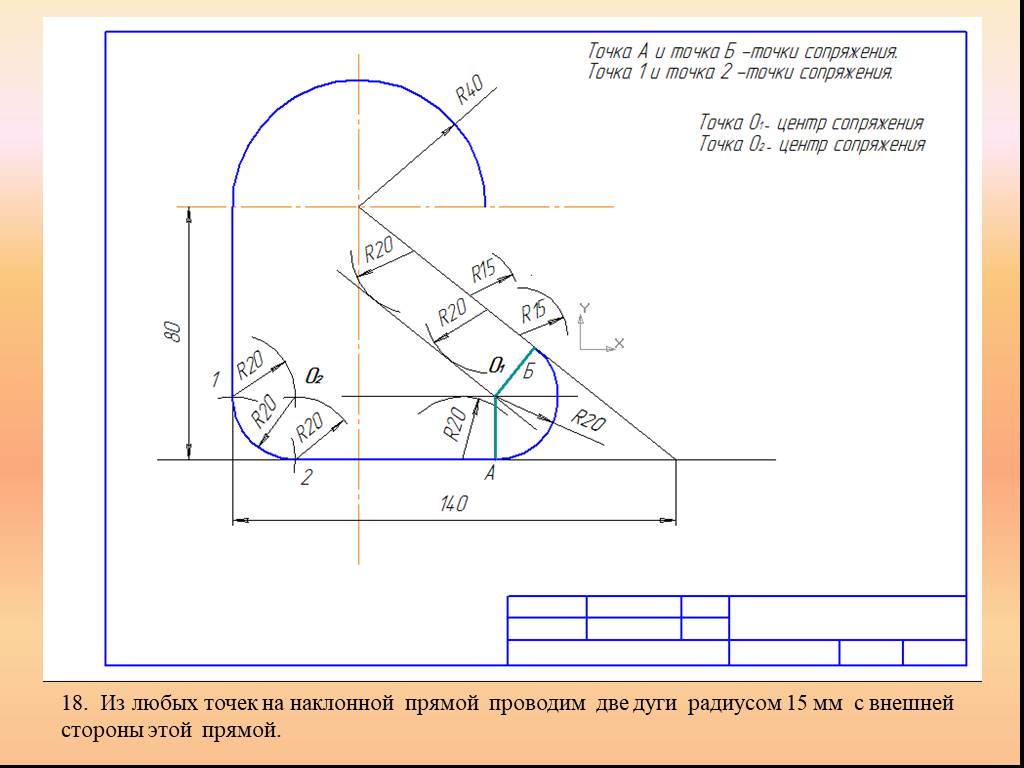
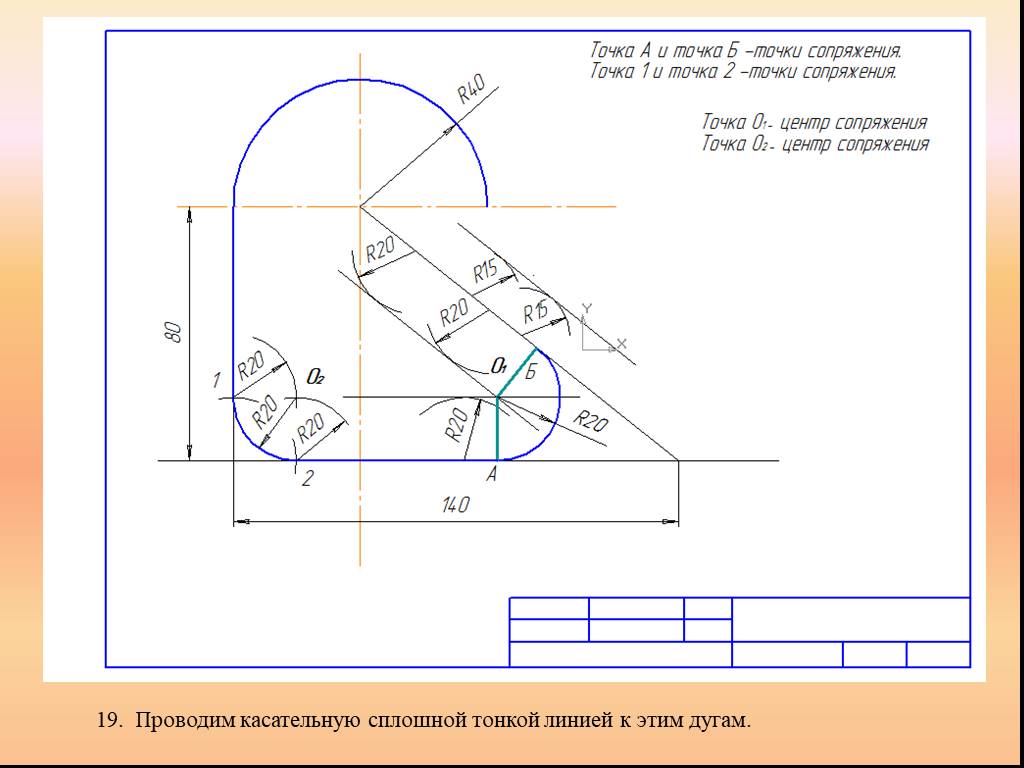
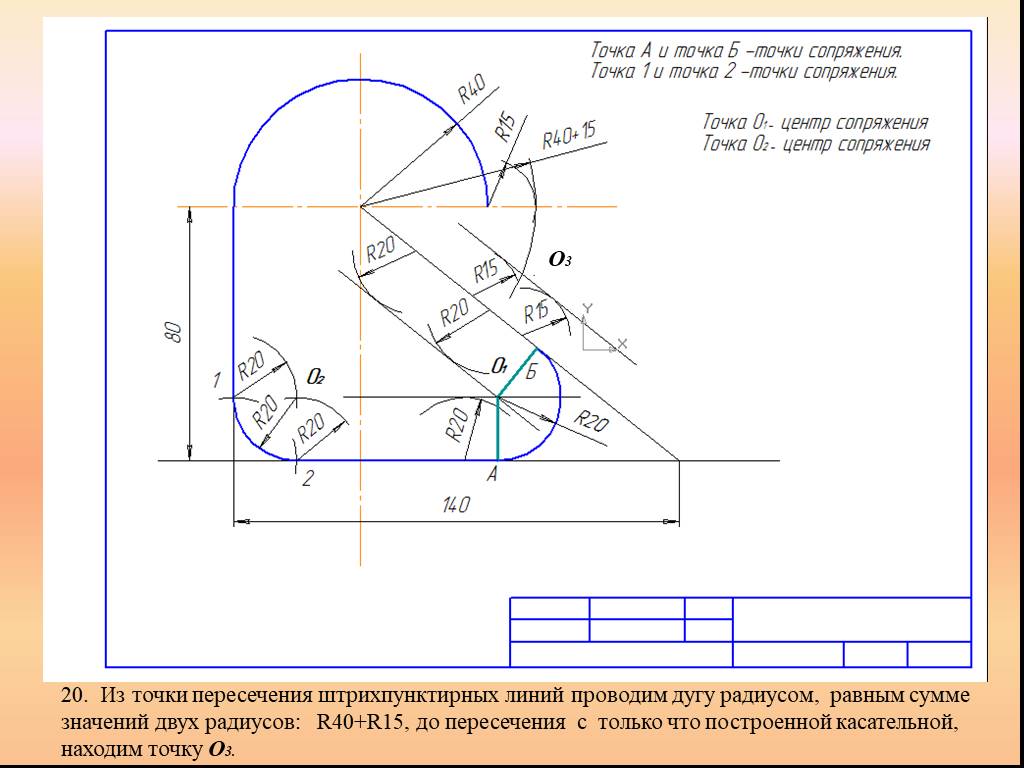
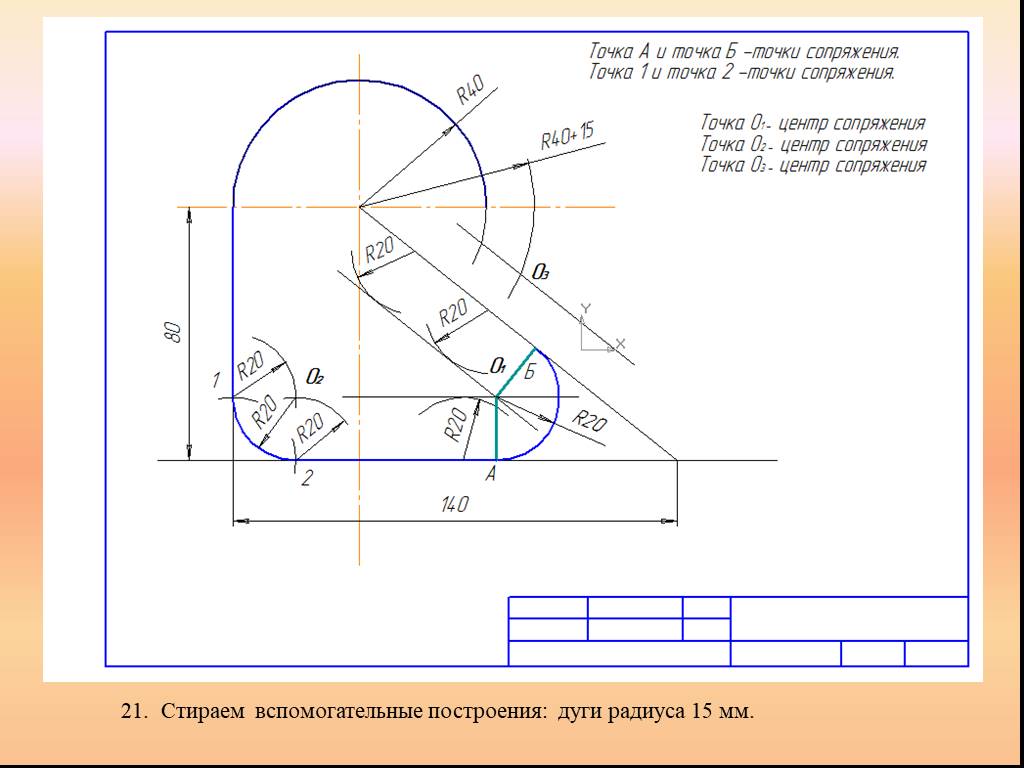
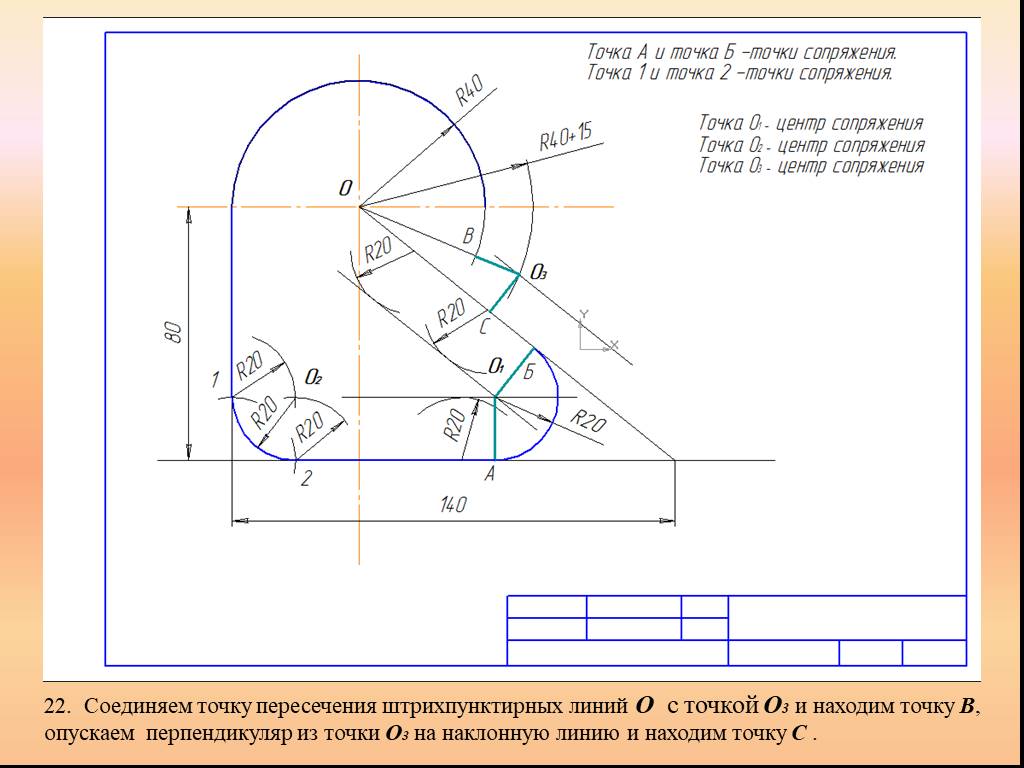
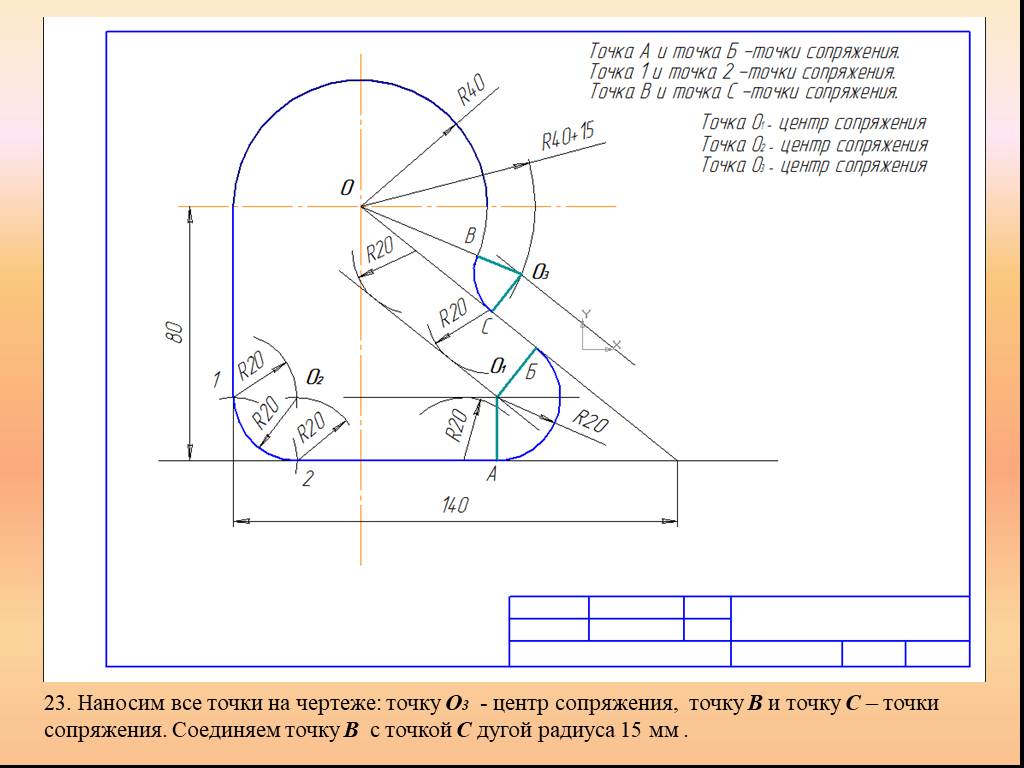
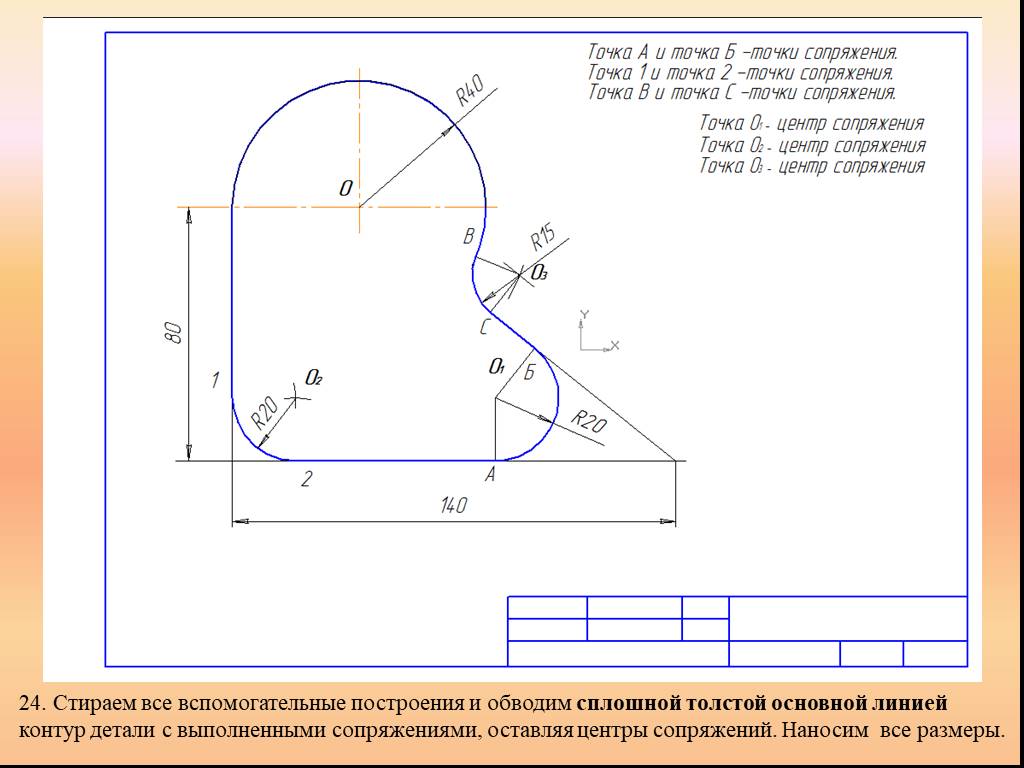
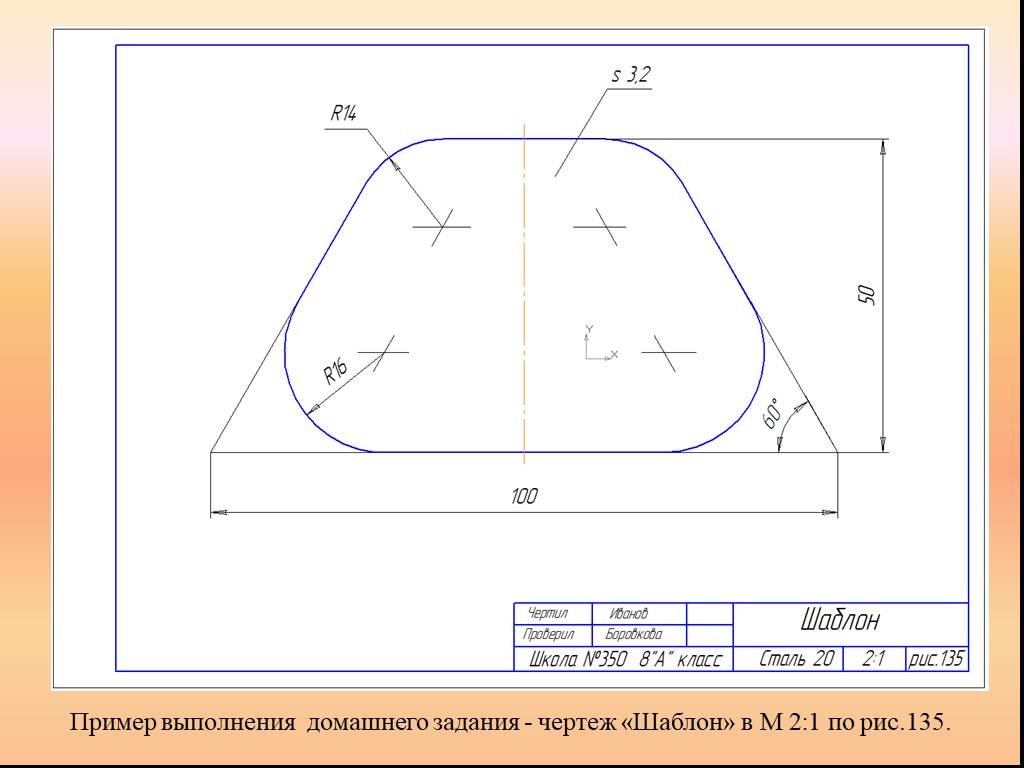
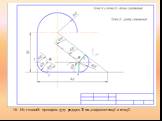
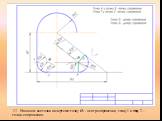
Презентация "Сопряжение. Геометрические построения" по математике – проект, доклад

ГБОУ СОШ №350 НЕВСКИЙ РАЙОН САНКТ-ПЕТЕРБУРГ

УЧИТЕЛЬ ЧЕРЧЕНИЯ БОРОВКОВА И.П.

2012 - 2013 УЧЕБНЫЙ ГОД

СОПРЯЖЕНИЕ. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ.

8 КЛАСС

Дать понятие о сопряжении, об элементах, обязательных в любом сопряжении. Ознакомить с правилами построения сопряжения двух прямых и с правилами построения сопряжения окружности и прямой дугой заданного радиуса . Продолжать развивать навыки работы с чертежными инструментами. Воспитывать стремление рационально выполнять учебные задания.

Цель:

Усвоить правила построения разного рода сопряжений. Выполнить чертеж шаблона, используя эти правила. Нанести размеры по ГОСТ 2.307-68.

Задачи для учащихся:

приобщение учащихся к графической культуре и к применению правил ЕСКД.

Задачи для педагога:

Сопряжением называют плавный переход одной

линии в другую.

100 мм 60 мм

Все построения выполняются на листе в клетку.

1. Проводим две штрихпунктирные тонкие линии: вертикальную линию на расстоянии 100 мм от вертикальной кромки форматаА4. горизонтальную линию на расстоянии 60 мм от верхней горизонтальной кромки листа ФА4.

2. Из центра пересечений штрихпунктирных линий проводим полуокружность сплошной толстой основной линией радиусом 40мм.

3. Откладываем от горизонтальной штрихпунктирной линии расстояние равное 80 мм и проводим горизонтальную сплошную тонкую линию.

4. Опускаем перпендикуляр из одного конца полуокружности сплошной тонкой линией до пересечения с горизонтальной прямой. Все построения выполняем тонкими линиями.

5. Откладываем на горизонтальной прямой вправо от вертикальной сплошной тонкой линии расстояние равное 140 мм и ставим точку.

6. Соединяем эту точку с центром пересечения штрихпунктирных линий. Размеры не наносим.

7. Из любых точек на горизонтальной прямой проводим две дуги радиусом 20 мм.

8. Проводим касательную сплошной тонкой линией к этим дугам.

9. Из любых точек на наклонной линии проводим две дуги радиусом 20 мм .

10. Проводим касательную сплошной тонкой линией к этим дугам и находим точку О1 - точку пересечения двух касательных.

О1

11. Из этой точки О1 опускаем два перпендикуляра на горизонтальную и наклонную линию соответственно, находим точку А и точку Б будущего сопряжения.

А Б

12. Из этой точки О1 проводим дугу радиуса 20 мм, соединяя точки сопряжения, т.е. точку А с точкой Б.

13. Наносим все точки на чертеже: точку О1 - центр сопряжения, точку А и точку Б – точки сопряжения.

14. Из точки пересечения вертикальной и горизонтальной прямых проводим дугу радиуса 20 мм, находим точку 1 и точку 2.

15. Из точки1 и точки 2 проводим две дуги радиуса 20 мм соответственно и находим точку О2 - точку пересечения этих дуг.

О2

16. Из точки О2 проводим дугу радиуса 20 мм, соединяя точку1 и точку2.

17. Наносим все точки на чертеже: точку О2 - центр сопряжения, точку 1 и точку 2 – точки сопряжения.

18. Из любых точек на наклонной прямой проводим две дуги радиусом 15 мм с внешней стороны этой прямой.

19. Проводим касательную сплошной тонкой линией к этим дугам.

О3

20. Из точки пересечения штрихпунктирных линий проводим дугу радиусом, равным сумме значений двух радиусов: R40+R15, до пересечения с только что построенной касательной, находим точку О3.

21. Стираем вспомогательные построения: дуги радиуса 15 мм.

22. Соединяем точку пересечения штрихпунктирных линий О с точкой О3 и находим точку В, опускаем перпендикуляр из точки О3 на наклонную линию и находим точку С .

23. Наносим все точки на чертеже: точку О3 - центр сопряжения, точку В и точку С – точки сопряжения. Соединяем точку В с точкой С дугой радиуса 15 мм .

24. Стираем все вспомогательные построения и обводим сплошной толстой основной линией контур детали с выполненными сопряжениями, оставляя центры сопряжений. Наносим все размеры.

Домашнее задание

1. Прочитать параграф 15.3, 15.4 и ответить на вопросы. 2. Выполнить аналогичную работу по рисунку 135 в масштабе 2:1 на белом листе формата А4, рамку и основную надпись с размерами по на рис.18 и рис.19. 3. Последовательность выполнения задания указана на рис. 134 и рис.135, а также пример выполнения чертежа смотри на сайте «2 берега» и в контакте.

Вопросы для проверки знаний.

Что называется сопряжением? Как называются элементы, обязательные для любого сопряжения? Где находятся точки сопряжения при построении сопряжения дуги окружности с прямой?

Пример выполнения домашнего задания - чертеж «Шаблон» в М 2:1 по рис.135.

ЛИТЕРАТУРА

1. Черчение: учебник для общеобразовательных учреждений / А.Д. Ботвинников, В.Н. Виноградов, И.С. Вышнепольский. — 4 –е изд., дораб. - М.: Астрель, 2012. —221 с.