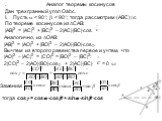
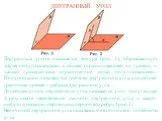
Презентация "Трёхгранный угол" по математике – проект, доклад
Презентацию на тему "Трёхгранный угол" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
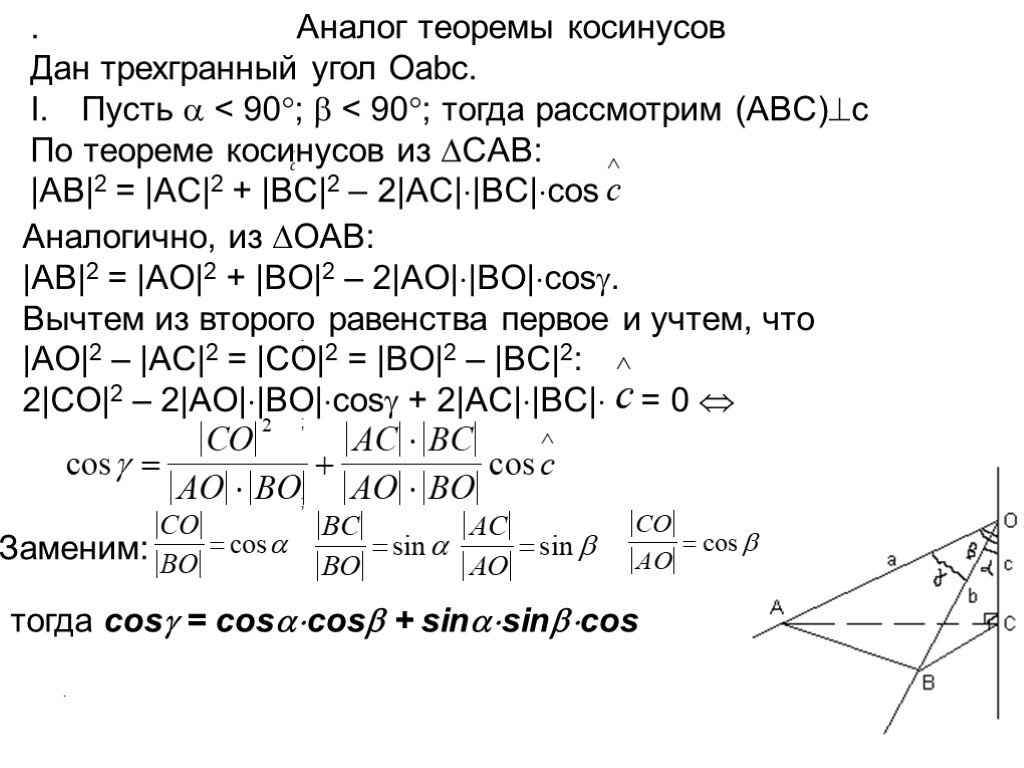
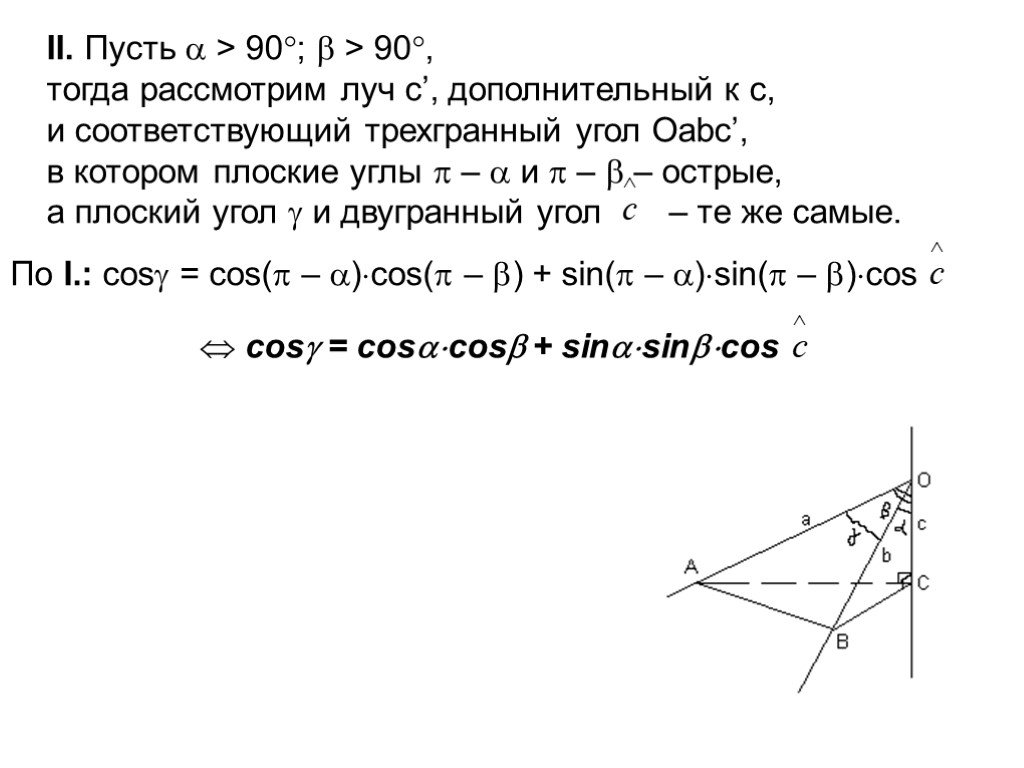
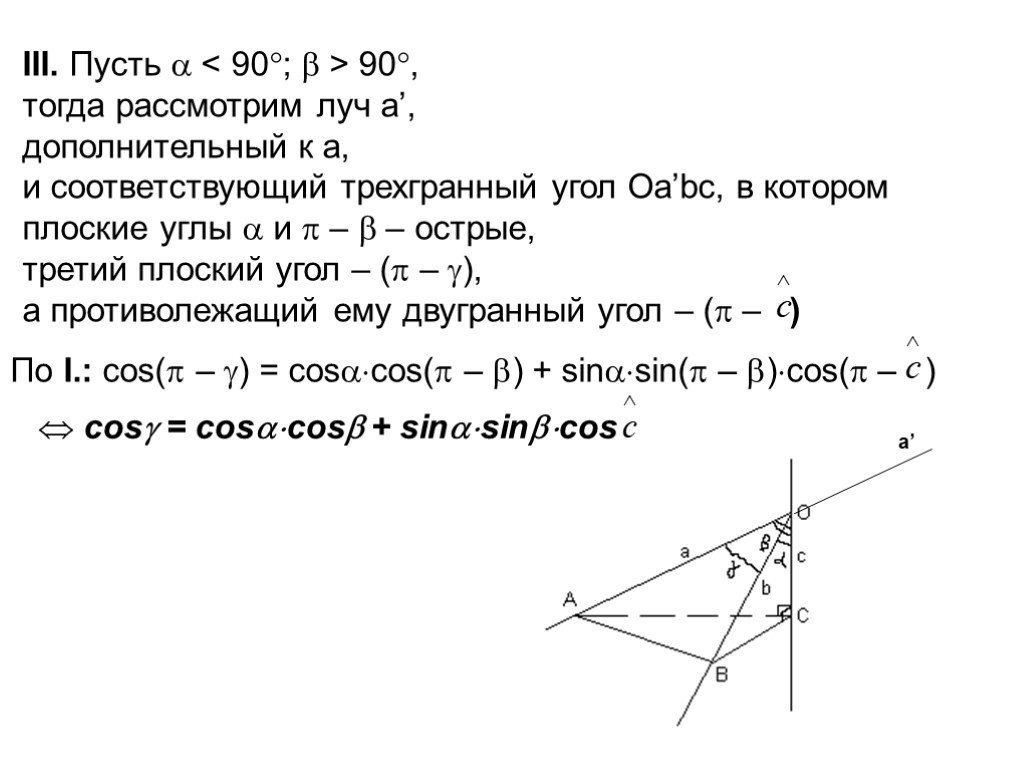
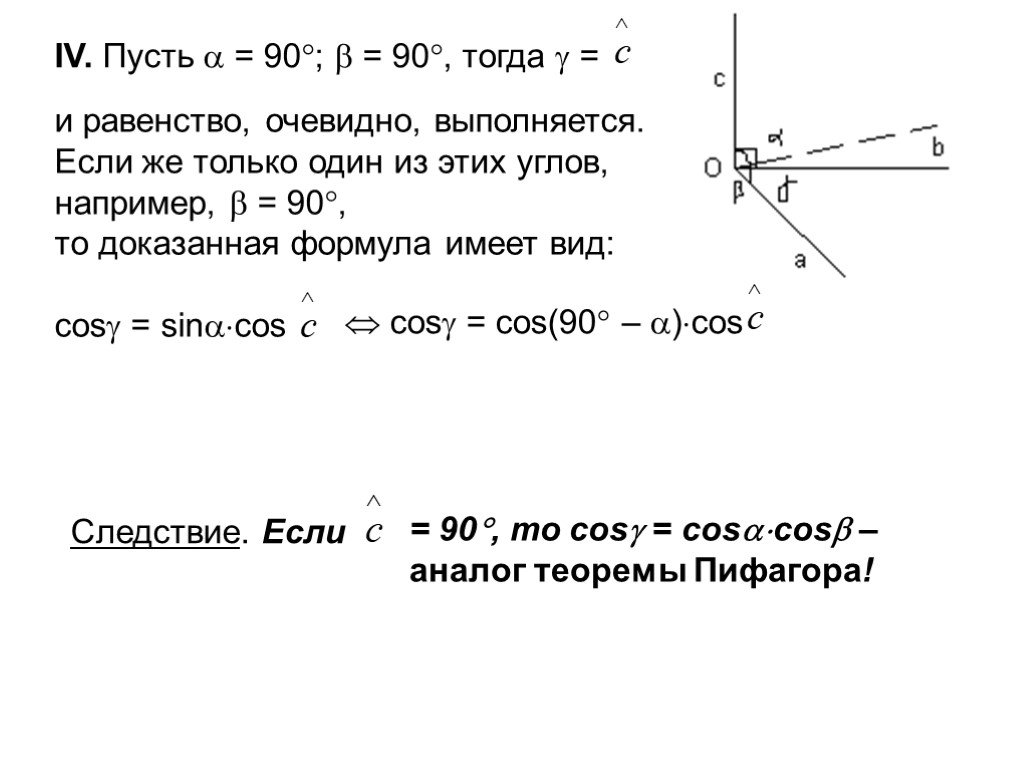
Слайды презентации
Список похожих презентаций
Луч и угол
Часть1. РЕШЕНИЕ ЗАДАЧ НА ПОВТОРЕНИЕ:. Дайте определение отрезка Какие понятия в геометрии считаются неопределимыми? Чем отличается теорема от аксиомы? ...Двугранный угол
Вдохновение есть расположение души к живейшему принятию впечатлений и соображению понятий, следственно, и объяснению оных. Вдохновение нужно в геометрии, ...Двугранный угол
Упражнение 1. Какой угол образует ребро двугранного угла с любой прямой, лежащей в плоскости его линейного угла? Ответ: 90о. Упражнение 2. Плоскости ...Двугранный угол
Основные задачи урока:. Ввести понятие двугранного угла и его линейного угла Рассмотреть задачи на применение этих понятий. Определение:. Двугранным ...Внешний угол треугольника. Теорема о внешнем угле треугольника
I. Cумма углов треугольника. 1. На доске доказать теорему о сумме углов треугольника: Сумма углов треугольника равна 1800 2. Решить задачу № 749 (чёт ...Внешний угол треугольника
Общий вид внешнего угла. Понятие. Свойство внешнего угла. Внешний угол. Внешний угол треугольника. Угол, смежный с каким–нибудь углом треугольника, ...Начальные понятия планиметрии. Прямая и отрезок. Луч и угол
Вводная беседа.Геометрия в переводе с греческого «землемерие» («гео»- по-гречески земля, а «метрео» - мерить).
Первым, кто начал получать геометрические ...
Внешний угол треугольника
Треугольник (музыкальный инструмент). Жесткость треугольников. Бермудский треугольник. ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА. У треугольника может быть два тупых ...Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Теорема 2. В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны ...Наглядная геометрия
«Геометрия является самым могущественным средством для изощрения наших умственных способностей и даёт нам возможность правильно мыслить и рассуждать» ...«Ломаная» геометрия
Найдите соответствие. Ответы. Ломаная Тема урока:. Какие из фигур являются ломаными? А Б В Г Д. Ответ А В Г. Кусок проволоки возьми И его ты перегни. ...Лобачевский и его геометрия
Гипотеза:. Любая теория современной науки считается единственно верной, пока не создана следующая. Невозможность доказать некоторое геометрическое ...Наглядная геометрия
КОНВЕРТ № 1 Откройте конверт. Соедини фигуры. КВАДРАТ. Двухмерное пространство Квадрат – плоская фигура. КОНВЕРТ № 2. Сравните фигуры Что у них общего? ...Занимательная геометрия
СОДЕРЖАНИЕ. 1. Обозначение точки. 2. Прямая линия. 3 .Введение правила. 4.Закрепление правила. Точка. А К Точка обозначается большими латинскими буквами. ...Из чего строится геометрия?
Если вообразить геометрию в виде огромного дома, то ученых, чьими трудами возведен этот дом, сравнить с каменщиками. Каждое утверждение опирается ...Загадочная и уникальная геометрия
Цель:. Показать значимость и актуальность геометрии в древние времена и настоящее время, ее взаимосвязь с другими науками на примере загадки египетских ...Древняя геометрия
еликие учёные древности. Развитие математики происходило в древнегреческой школе, основателем которой был легендарный Пифагор (564-473 г.г. до н. ...Геометрия Евклида и геометрия Лобачевского. Сходства и отличия
Евклидова геометрия. Евкли́д или Эвкли́д (, ок. 300 г. до н. э.) — древнегреческий математик. Мировую известность приобрёл благодаря сочинению по ...Влияет ли геометрия города на его образ?
Тема : «Влияет ли геометрия города на его образ?» Объект исследования: объектом исследования является расположения и схемы городов. Предмет исследования: ...«Конус» геометрия
История изучения геометрического тела конус. С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки. ...Конспекты
Двугранный угол
Тема урока: «Двугранный угол». Ф.И.О. учителя:. Банникова Дарья Дмитриевна. Дата проведения:. 26.02.13. Класс:. 10 «Б». . Цели урока:. Ввести ...Прямой и непрямой угол
Тема: Прямой и непрямой угол. . Цели урока:. *познакомить с прямым и непрямым углом;. . *закреплять вычислительные навыки;. . *развивать ...Виды углов. Прямой угол
Автор: Малахова Галина Григорьевна, учитель начальных классов МКОУ СОШ № 17 села Сухая Буйвола, Петровского района, Ставропольского края. . Виды ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 декабря 2018
Категория:Математика
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию