Конспект урока «Уравнения» по математике для 1 класса
Урок открытия новых знаний по теме "Уравнения"
(учебник Л.Г. Петерсон "Математика", 1-й класс)
Учитель: Горелова Наталья Петровна
Цель: Сформировать способность решать уравнения на основе взаимосвязи между частью и целым.
Задачи:
-Активизировать умение решать простые задачи на сложение и вычитание;
-Тренировать автоматизированный навык счета в пределах 9.
-Развивать мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, синтез, обобщение.
-Создавать мотивацию к учебной деятельности на уроке посредством создания проблемной ситуации.
-Привитие умения работать в группе, паре, воспитание чувства товарищества, взаимопомощи.
Оборудование: интерактивная доска (ИД), компьютер, проектор, ноутбуки; учебник-тетрадь (3 часть), схемы задач, карточки с примерами, корзины с «плюсами», карточки-пазлы.
Класс разделен на 4 группы, в каждой группе – капитан.
1.Организация учебного процесса на этапе.
На ИД открыт девиз урока:
В школу мы пришли учиться
В жизни это приходиться
Тот, кто хочет много знать
Должен сам все постигать.
- Ребята, согласны ли Вы с содержанием девиза урока?
-Как Вы понимаете, что учение пригодится в жизни? (Без знаний ничего не сделаешь)
- Выделите главное слово в последних двух строчках и объясните свой выбор.
(Слово "сам", т.к. мы учимся тогда, когда сами понимаем, чего мы не знаем и сами открываем новые знания.)
Личностные УУД (смыслообразование)
2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
Цели:
Актуализировать умение решать примеры на нахождение целого и части.
Тренировать вариативность мышления, мыслительные операции: сравнение, анализ, обобщение.
Мотивировать к пробному действию и его самостоятельному выполнению.
Организовать фиксацию образовательной цели и темы урока.
-Чтобы и сегодня открыть новые знания, нам нужно повторить раннее изученное и собрать плюсики в нашу корзину "Знаний".
Готовы? Начнем урок с устного счета.
-
Дан ряд чисел 4 5 9
-Назовите самое большое и самое маленькое число в этом ряду.
-Назовите число, которое является суммой двух других чисел
-На сколько 9 больше 4? На сколько 4 меньше 9?
-Как узнать, на сколько одно число больше или меньше другого?
-Назовите числа, которые можно заменить суммой одинаковых слагаемых?
-Установите закономерность и продолжите ряд на 3 числа (10, 14, 15)
-Расскажите все, что знаете о числе 9.
-С каким числом будет связан устный счет?
Коммуникативные УУД (постановка вопроса)
Познавательные УУД (общеучебные, логические)
2) Работа с диском «Уроки Кирилла и Мефодия» часть 3, урок 24
Задание 2 –состав числа 9
Задание 9 –компоненты суммы
Задание 13 –собрать пазлы (решить примеры)
Познавательные УУД(общеучебные, логические)
Коммуникативные УУД (планирование)
3)Работа с задачами, схемами задач
-Что неправильно в задачах? Исправьте, подберите схему и решите.
А) Мама купила 9 тарелок, две тарелки съели за столом. Сколько тарелок осталось?
Б) Наташа вырезала 9 квадратов. 4 квадрата она раскрасила.
В) Юля прочитала 9 страниц. Сколько страниц ей осталось прочитать?
Дети выбирают схему из предложенных на доске, заполняют ее, устно решают, называют ответ.
Познавательные УУД(общеучебные, логические)
Регулятивные УУД (планирование)
4)Предлагаю каждой группе решить примеры на карточке.
| 2+4 | Р | 4-2 | И | 5+4 | |
| У | 6-5 | Я | 2+8 | А | 9-6 |
| Н | 5+3 | Е | 10-3 | В | 0+5 |
Проверка на ИД: записывают ответы
- Распределите (устно) примеры на 2 группы и объясните.
(1 группа - примеры на сложение, находим целое.)
(2 группа - примеры на вычитание, находим часть.)
- Молодцы! В вашей корзине "Знаний" +.
Познавательные УУД (выбор оснований и критериев для сравнения, классификации объектов; общеучебные)
Регулятивные УУД (волевая саморегуляция)
3. Выявление места и причины затруднения.
Цель: Выявить и зафиксировать место и причину затруднения.
3.1. -Вставьте в окошко пропущенное число
…+3=9
(9 - это 6 и 3, поэтому вставим 6, получаем 6+3 = 9).
-Это равенство с "окошком" или с неизвестным числом. Хотите узнать, как называется такое равенство?
Запишите в таблицу ответы примеров в порядке возрастания и прочтите полученное слово.
На ИД появляется слово УРАВНЕНИЕ
- Знакомо ли вам такое слово. Встречалось ли оно вам раньше?
- Какая же будет тема урока? (Уравнение).
- Какую цель поставим перед собой? (Узнать, что такое уравнения и научиться их решать.)
-Действительно, в математике называют такие равенства уравнениями. Неизвестный компонент чаще всего в математике обозначают латинской буквой Х (икс).
-Поставим его в "окошко" и получим равенство. Прочтем запись.
- х+3=9 - это уравнение.
х=6 - корень уравнения.
-Мы решили уравнения с помощью подбора.
-Что значит решили? (Подобрали такое число Х, при котором равенство верно.)
Коммуникативные УУД (постановка вопроса)
Познавательные УУД (общеучебные)
Регулятивные УУД (контроль)
3.2. Наша работа продолжается.
Работа в учебнике на с.20 №1.
-Как вы думаете, что нужно сделать в этом задании? (Надо подобрать предметы в мешок - часть, так, чтобы получилось верное равенство.)
- Как называются такие равенства? (Уравнения).
- Верно ли решено первое уравнение? Докажите.
Решите уравнения по группам.(по одному уравнению каждой группе)
Проверка: на ИД эталон решения
Познавательные УУД(общеучебные, логические)
Коммуникативные УУД (постановка вопроса)
3.3. - Молодцы, вы все справились с заданием и теперь решите самостоятельно уравнение на карточке.(групповая работа)
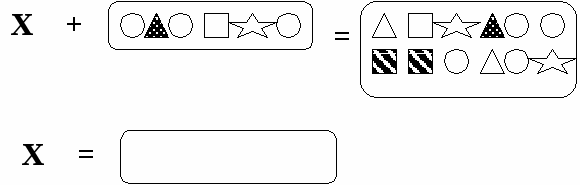
- Какое задание выполняли? (Решали уравнения, в котором неизвестна часть).
-Чему равен х? (Появляются разные ответы.)Затруднения.
- Чем это задание отличается от предыдущего? (Много фигур, они разной формы и цвета.)
- А в чем возникло затруднение? (Мы путаемся).
- Если фигур становится больше - легче или труднее будет подбирать решение? (Труднее).
- Значит метод подбора подходит для небольшого количества фигур, а для большого количества нужен другой способ.
-Какая же наша задача? (Найти новый способ решения уравнений).
Познавательные УУД (формулирование проблемы)
Познавательные УУД (общеучебные, логические)
Регулятивные УУД (целеполагание)
Коммуникативные УУД (планирование)
4. Построение проекта выхода из затруднения.
Цель:
Уточнение цели проекта (открыть правило решения уравнения с неизвестной частью (слагаемым)).
-Наша цель - придумать, как по - другому найти неизвестную часть в уравнении, который можно использовать для решения любых уравнений.
-Какими знаниями для решения можем воспользоваться? (Знаем части и целое)
- Назовите их в уравнении. (Первый мешок - часть неизвестна. Второй мешок - часть известен, и известно целое)
- Какие правила о взаимосвязи частей и целого, как "волшебный ключик" помогают нам в самых разных ситуациях? ИД
Правило1: Целое равно сумме частей.
Правило 2: Чтобы найти часть, надо из целого вычесть часть.
- А теперь каждый из вас должен догадаться какое из этих правил подойдет? (дети предлагают способ).
- Вычтите из обеих частей равенства поровну - фигурки из первого мешка. Обозначьте вычитание зачеркиванием. ИД
- Удобно так искать неизвестное слагаемое? (Да)
- Какое правило нам помогло. (Нахождение части.)
Познавательные УУД (общеучебные, логические)
Коммуникативные УУД (постановка вопроса)
Регулятивные УУД (контроль)
5. Реализация построенного проекта.
Цель:
Организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостаточных знаний.
Организовать решение уравнений и зафиксировать преодоление затруднений.
Определение средств (алгоритм, учебник).
Построение плана достижения цели.
5.1. Дети в группе составляют план для решения уравнений
Проверка: ИД, функция «занавес»
Учитель предлагает план проговаривания решения уравнений.
5.2.Учебник с.20 №3.(фронтальная работа)
- Что было известно? (одна часть, целое.)
- Что требовалось найти? (Другую часть)
- Чему же равна неизвестная часть или х ?
-Смогли преодолеть затруднения? (Да)
- Что вам помогло? ("Секрет") (Правило нахождения части.)
- Что позволяет вам открытый новый способ? (Решать уравнения)
Познавательные УУД (общеучебные, логические)
Регулятивные УУД (планирование, контроль)
Коммуникативные УУД (постановка вопроса)
Личностные УУД (самоопределение)
6. Первичное закрепление во внешней речи.
Цель: Создать условия для фиксации изученного способа действия во внешней речи.
6.1. Работа в парах с.20№4. (Решают уравнения.)
-Правило работы в парах: Каждый в паре имеет право высказать свое мнение, пока один говорит, другой должен внимательно слушать.
Учащиеся выполняют задания в парах с комментированием по плану.
Проверка организуется по эталону на ИД. Самооценка.
6.2. С.21№5 (а) с комментированием
Познавательные УУД (общеучебные, логические)
Коммуникативные УУД (управление поведением партнёра точностью выражать свои мысли)
Регулятивные УУД (планирование, контроль, оценка, волевая саморегуляция)
Личностные УУД (самоопределение)
7. Обработка умений по применению нового способа.
Цель:
Организовать самостоятельное выполнение учащимися заданий на новый способ действий.
Организовать самооценку детьми правильности выполнения заданий.
7.1. Самостоятельная работа с самопроверкой по эталону с.21 №5 б), в)
Самооценивание.
-У кого есть ошибки? В чем они.
-Сделайте вывод. Проверьте по эталонам.
Познавательные УУД (общеучебные, логические)
Регулятивные УУД (планирование, контроль, коррекция, оценка, волевая саморегуляция)
8.Контроль полученных знаний
Цель: проверка умений учащихся решать уравнения по плану.
Работа в группе с тренажером, оценивает компьютер.
Познавательные УУД (общеучебные, логические)
Коммуникативные УУД (постановка вопроса)
Регулятивные УУД (планирование, контроль, оценка, волевая саморегуляция)
9. Рефлексия учебной деятельности на уроке.
Цель:
Зафиксировать новое содержание, изученное на уроке.
Оценить собственную деятельность на уроке.
-Вот и все! Напоследок только оглянемся назад. Какую цель перед собой ставили. (Узнать, что такое уравнение и научиться их решать)
- Достигли своей цели? (Да)
- Докажите. (Уравнение - это равенство с неизвестным числом и чтобы его решить надо следовать плану. Чтобы найти неизвестную часть надо из целого вычесть известную часть)
- Что дает нам новое знание? (Научились сами и теперь можем научить других.)
-Просмотрите еще раз свою работу на уроке и оцените себя. (Понятно, интересно, работал) Что оцениваете на 1 шкале? (Как было понятно.) На второй? (Насколько было интересно на уроке.) На третьей? (Как я работал на уроке.)
Учащиеся в группах на специальных листах заполняют шкалы.
(Капитаны команд складывают плюсики в большую корзину.)
- Знание собирается по капле. И сегодня мы постарались, хоть немного, но пополнить имеющиеся знания, ведь из маленьких открытий и умений строится большое знание!
Личностные УУД (смыслообразование, нравственно-этическое оценивание)
Регулятивные УУД (оценка, волевая саморегуляция)
Горелова Наталья Петровна, учитель начальных классов МОУ «Средняя общеобразовательная школа №12 с углубленнным изучением английского языка» Чистопольского муниципального района РТ г.Чистополь, ул.Ак.Королева, д.5
Рабочий телефон: (8-84342)-4-72-09
Сотовый: 8-927-44-00-170
e-mail: gorelowa2011@mail.ru
Здесь представлен конспект к уроку на тему «Уравнения», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (1 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

