Конспект урока «Методы решения логарифмических уравнений» по алгебре для 11 класса
![]()
Муниципальное бюджетное общеобразовательное учреждение
«Общеобразовательная Хетовская средняя школа»
Виноградовского района Архангельской области
Конспект урока по алгебре и началам анализа
в 11 классе
«Методы решения логарифмических ![]() уравнений»
уравнений»
подготовила
учитель математики
Воробьева Любовь Михайловна
п.Хетово
2014
Тема урока: «Методы решения логарифмических ![]() уравнений»
уравнений»
Тип урока: повторительно-обобщающий.
Цели урока:
Образовательные: обобщить и систематизировать знания учащихся о логарифме и его свойствах; умения решать логарифмические уравнения различными методами.
Развивающие: развивать творческую и мыслительную деятельность учащихся, способствовать формированию навыков коллективной работы, развивать умение четко и ясно излагать свои мысли.
Воспитательные: формирование интереса к предмету.
1.Повторение определения и свойств логарифмов. Поставьте в соответствие:
| logapb | 1 | logab | |
| 2 | logab+logac | 2 | nlogab |
| 3 | logab-logac | 3 | loga(bc) |
| 4 | alogab | 4 | b |
| 5 | logabn | 5 | logcb |
| 6 | logab/logac | 6 |
|
Методы решения логарифмических уравнений
1. Уравнения, решаемые по определению.
logab=c,тогда ас=в,а>0, b>0,а![]() .
.
Примеры
а)log24![]() =Х б) logx64=3
=Х б) logx64=3
х3=64
2х=25/2 х=4
х=5/2
2. Метод потенцирования. Он основан на теореме: Если f(х)>0и g(х)>0,то логарифмическое уравнение logaf(х)=logag(х), (а>0,а![]() ) равносильно уравнению f(х)=g(х).
) равносильно уравнению f(х)=g(х).
Решите уравнение:
lg(х+4)+lg(2х+3)=lg(1-2х).
Решение: Данное уравнение равносильно:
lg(х+4)(2х+3)=lg(1-2х), 2х2+13х+11=0,
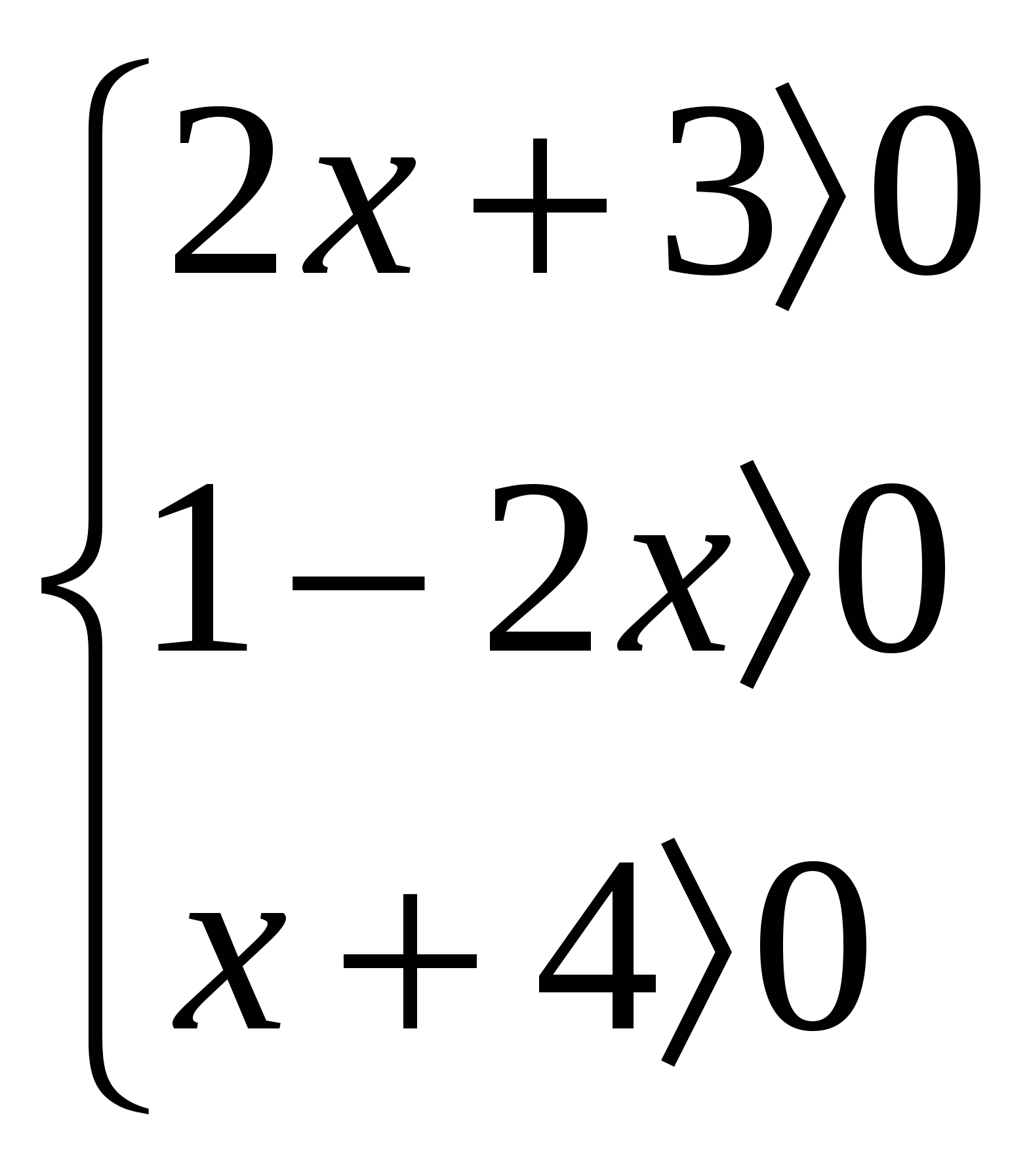 ,
, ![]()
![]() >х>-
>х>-![]()
![]()
Ответ: -1.
3. Метод введения новой переменной.
Решите уравнение: а) 4-lgх=3![]() .
.
Решение: Воспользуемся методом замены. Пусть ![]() =t,тогда данное уравнение примет вид t2+3t-4=0,откуда t1=1,t2=-4(посторонний корень).
=t,тогда данное уравнение примет вид t2+3t-4=0,откуда t1=1,t2=-4(посторонний корень).
Следовательно,![]() =1, lgx=1, х=10.
=1, lgx=1, х=10.
Ответ:10
б) lg2x-3lgx+2=0, О.Д.З.х>0.
Пусть lgx=t, t![]() R,
R,
t2-3t+2=0, t1=1,t2=2.
Если t1=1,то lgx=1,х=10., если t2=2,то lgx=2,х=100.
Ответ: х1=10, х2=100.
4. Функционально-графический метод.
Решите уравнение: lgx=11-х.
Так как функция у=lgx возрастает, а функция у=11-х убывает , то заданное уравнение имеет только один корень, который легко можно найти. При х=10 данное уравнение обращается в верное числовое равенство 1=1.
Ответ:х=10.
5. Метод приведения к одному основанию.
logab=logcb/logca, а>0, в>0, с>0, а![]() , с
, с![]() .
.
Решите уравнение: log2х+log4х+log16х=7.
Решение. Перепишем уравнение в виде:
log2х+0,5log2x+0,25log2x=7![]() log2x+2log2x+log2x=28
log2x+2log2x+log2x=28![]() log2x=4.
log2x=4.
Ответ: 16.
6. Метод логарифмирования.
Иногда встречаются уравнения, в которых фигурирует функция вида y=f(x)g(x),при этом чаще всего подразумевается, что f(x)>0. Такие уравнения удобно решать почленным логарифмированием.
Решите уравнение: хх+2=х5.
Решение: хх+2=х5 ![]() lgxx+2=lgx5
lgxx+2=lgx5![]() (x+2)lgx=5lgx
(x+2)lgx=5lgx![]() (x-3)lgx=0
(x-3)lgx=0
Ответ:1;3 .
7. Использование свойств монотонности функции.
Пример: log3(x+1)+log4(5x+6)=3 О.Д.З. х>-1,2.
у=log3(х+1)-возрастающая функция, у=log4(5х+6)-возрастающая функция, 3-const. Сумма двух возрастающих функций равна возрастающей функции.
Используем утверждение: если возрастающая функция равна const или убывающей функции, тогда уравнение имеет один корень, который находится с помощью метода подбора.
Ответ:х=2.
8. Использование свойств ограниченности функции.
Пример: log2(17-│sin0,5пх│)=![]() 2,
2,
Рассмотрим левую часть: так как 0≤│sin0,5пх│≤1,то log2(17-│sin0,5пх│)≥log216=4,то есть л.ч.≥4 при х=1 достигается равенство.
Рассмотрим правую часть ![]() 2=
2=![]() 2 ≤
2 ≤![]() =4,
=4, ![]() 2≤4,при х=1 достигается равенство.
2≤4,при х=1 достигается равенство.
Ответ:х=1.
9. Однородные уравнения 2 степени.
ах2 + вху + су2=0 │:у2≠0, а(х ∕у)2+в(х ∕ у)+с=0, аt2+вt+c=0 .
Пример: 3log22(х+1)-4log2(2x+1)log2(x+1)+log22(2x+1)=0, О.Д.З.х>-0,5, делим на log22(2x+1) и log2(x+1) ∕log2(2х+1)=t, получаем уравнение вида: 3t2-4t+1=0, t1=1, t2=![]() .
.
log2(x+1) ∕ log2(2x+1)=1, log2(x+1)=log2(2x+1), х+1=2х+1, х=0.
log2(x+1)/ log2(2x+1)=![]() , 3log2(x+1)=log2(2x+1), (х+1)3=2х+1,
, 3log2(x+1)=log2(2x+1), (х+1)3=2х+1,
х3+3х2+3х+1=2х+1 , х(х2+3х+1)=0 х1=0, х2=![]() , х3=
, х3=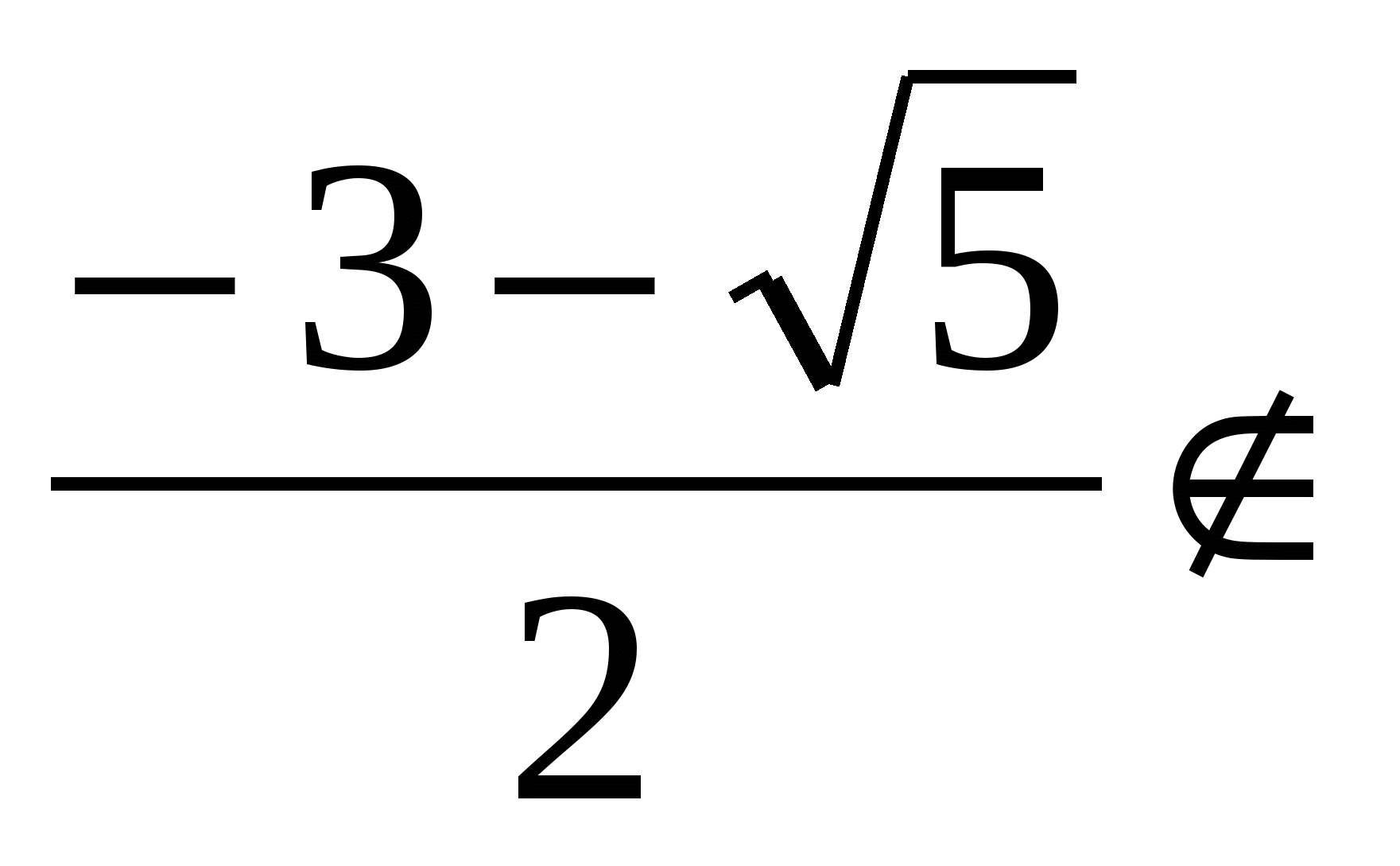 О.Д.З.
О.Д.З.
Ответ: х=0, х =![]() .
.
10. Использование формулы: аlogcb=blogca, в>0, а.>0, с>0, в≠1,а≠1,с≠1.
Пример: 3хlog52+2log5x=64, О.Д.З. х>0,
3∙2log5x+2log5x=64, 2log5x=16 , log5х=4 , х=625.
Ответ: х=625.
Подведение итогов.
Домашнее задание. Решите уравнения:
1).log2![]() +log2(х2-25)=0. Ответ:х=6.
+log2(х2-25)=0. Ответ:х=6.
2) 3х+1=5х-1. Ответ: log5∕315.
3)log2x+1(5+8x-4x2)+log5-2x(1+4x+4x2)=4.Ответ: 0,5; 1.
4)2+6log8x=log2(6х+18).
5)log3x+log9x+log27x=![]() .
.
Литература
1.А.Г.Мордкович «Алгебра и начала анализа» -учебник, задачник 10-11 классы.
2. «Тренировочные задания ЕГЭ повышенной сложности». Г.И.Ковалева и др. «Учитель» Волгоград
3. П.В.Чулков «Уравнения и неравенства в школьном курсе математики», лекции 5-8.
4. «Математика ЕГЭ. Эффективная подготовка» Л.Д.Лаппо, М.А.Попов «Экзамен» Москва.
![]()
Здесь представлен конспект к уроку на тему «Методы решения логарифмических уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

