Конспект урока «Методы решения систем уравнений» по алгебре для 9 класса

МУНИЦИПАЛЬНОЕ КАЗЕННОЕ

ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №5» г.Михайловска

Методическое объединение учителей математики, физики, информатики

Математика

План–конспект урока алгебры в 9 классе

Тема: Методы решения систем уравнений.

Автор:

Воеводина Алла Анатольевна

учитель математики

г.Михайловск

2014-2015 гг

Тема: Методы решения систем уравнений.

Тип урока: урок закрепления и систематизации знаний учащихся.

Цели урока:

• закрепить навыки решения систем уравнений второй степени различными способами: графическим, способом подстановки, способом сложения;

• формирование представлений о структуре заданий по теме: «Системы уравнений» в заданиях ГИА, а также их уровне сложности;

• создать ситуацию успешности каждого учащегося, воспитать чувство ответственности, самостоятельности;

• развить внимание, память, логическое мышление.

Оборудование: карточки для индивидуальной работы, сигнальные карточки, оценочный лист, тесты, проектор.

Формы организации: фронтальная, индивидуальная, парная.

Ход урока

1. Орг.момент.

Мотивация учения.

Французский писатель Анатоль Франс заметил “Чтобы переварить знания надо поглощать их с аппетитом”, последуем совету писателя, будем на уроке активны, внимательны, будем “поглощать” знания с большим желанием. Умение решать системы уравнений позволяет существенно расширить класс текстовых задач и перед нами стоит задача: повторить способы решения систем уравнений, проверить свое умение самостоятельно применять полученные знания и дать им самооценку.

{- Записать в тетрадь число и тему урока}

2.Актуализация знаний и умений

Фронтальный опрос: (вопросы на слайде)

а) Что является решением уравнения с двумя переменными?

б) Что значит решить уравнение с двумя переменными?

в) Что называется решением системы уравнений с двумя переменными?

г) Какие системы называются равносильными?

д) Какие способы решения систем уравнений вы знаете?

е) Каким способом удобнее всего решить данный пример? (примеры на слайде)

Одновременно с фронтальным опросом три ученика на доске решают систему уравнений из домашней работы разными методами: графическим, методом подстановки, методом сложения, и рассказывают алгоритм решения. Проверяем вместе графический способ (на слайде)

- Возьмите оценочные листы, поставьте себе оценку за первый этап работы.

3. Проверка умений применять на практике полученные знания.

1) Графический способ решения.

III ряд работает в парах.

- Возьмите карточку № 1 . На ней изображены графики некоторых уравнений, а справа записаны системы уравнений. Но в этой системе одного уравнения не хватает. Ваша задача заключается в том, чтобы:

1. в систему вписать уравнение линии, изображенной на чертеже

2. дополнить чертеж графиком, уравнение которого уже записано в системе,

3. найти решение данной системы графически.

Время работы 10 минут. Проверить решения, ответы на слайде.

I, II ряды работают в тетради.

- Выяснить, сколько решений имеет система уравнений?

(Устно) а) 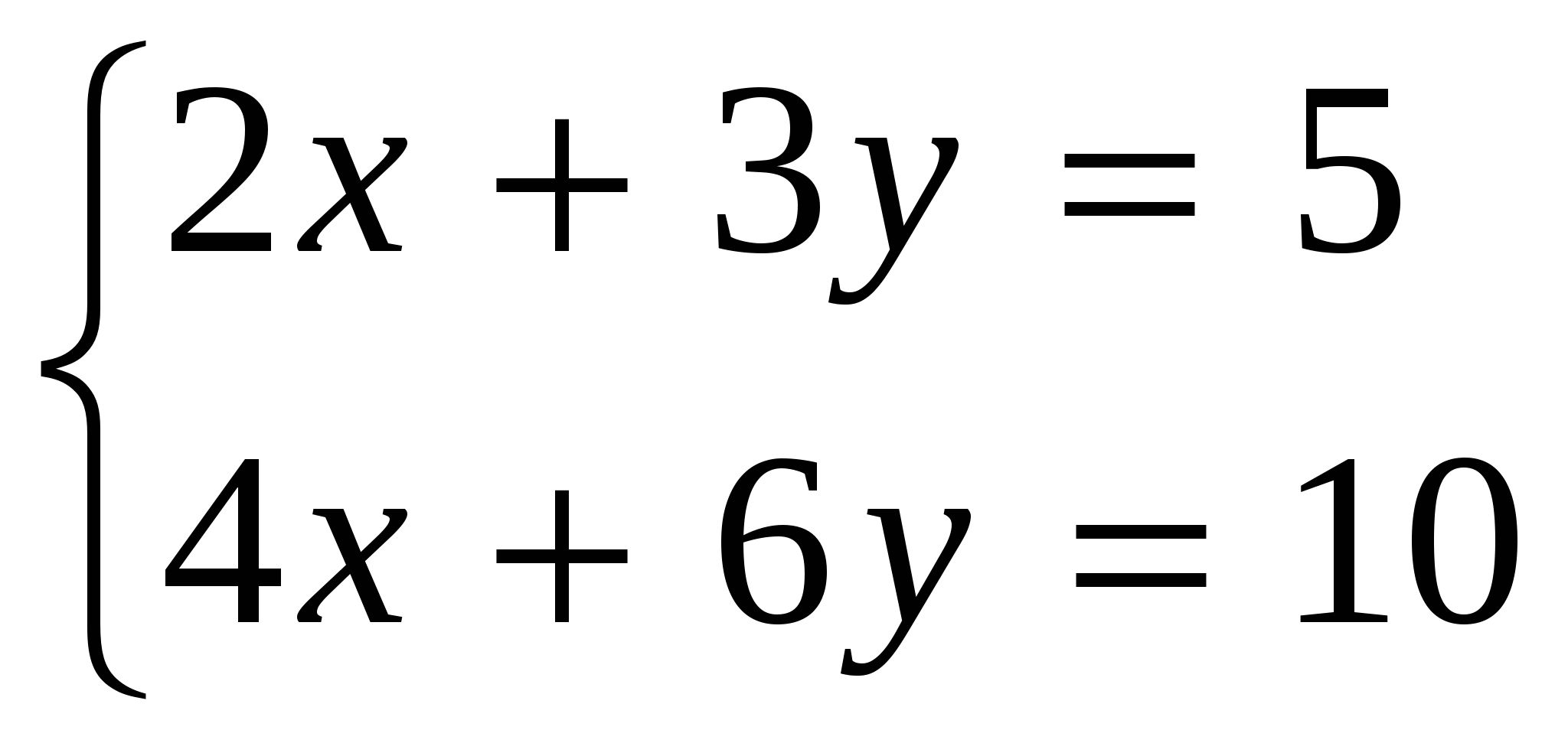б)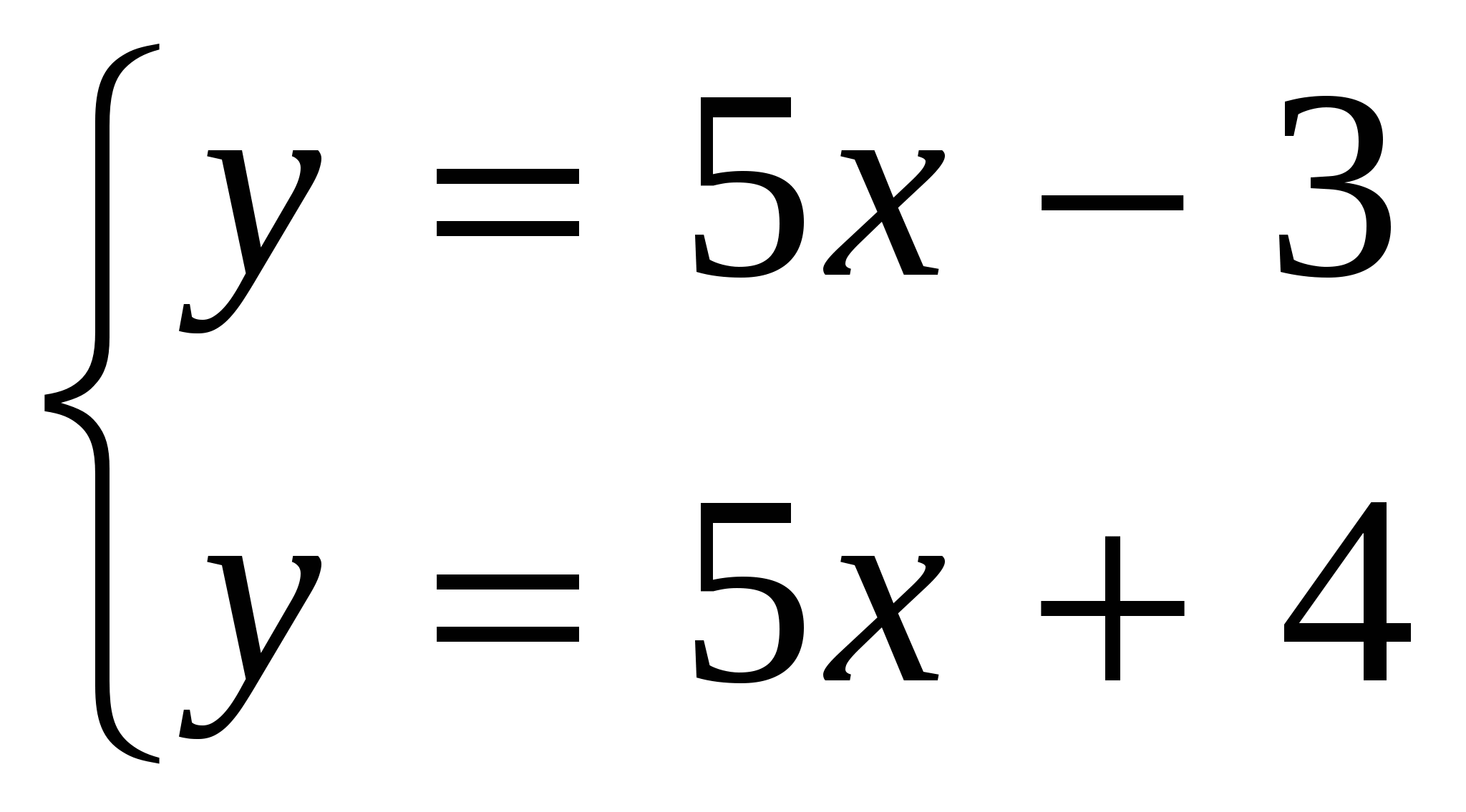

(На доске) в) 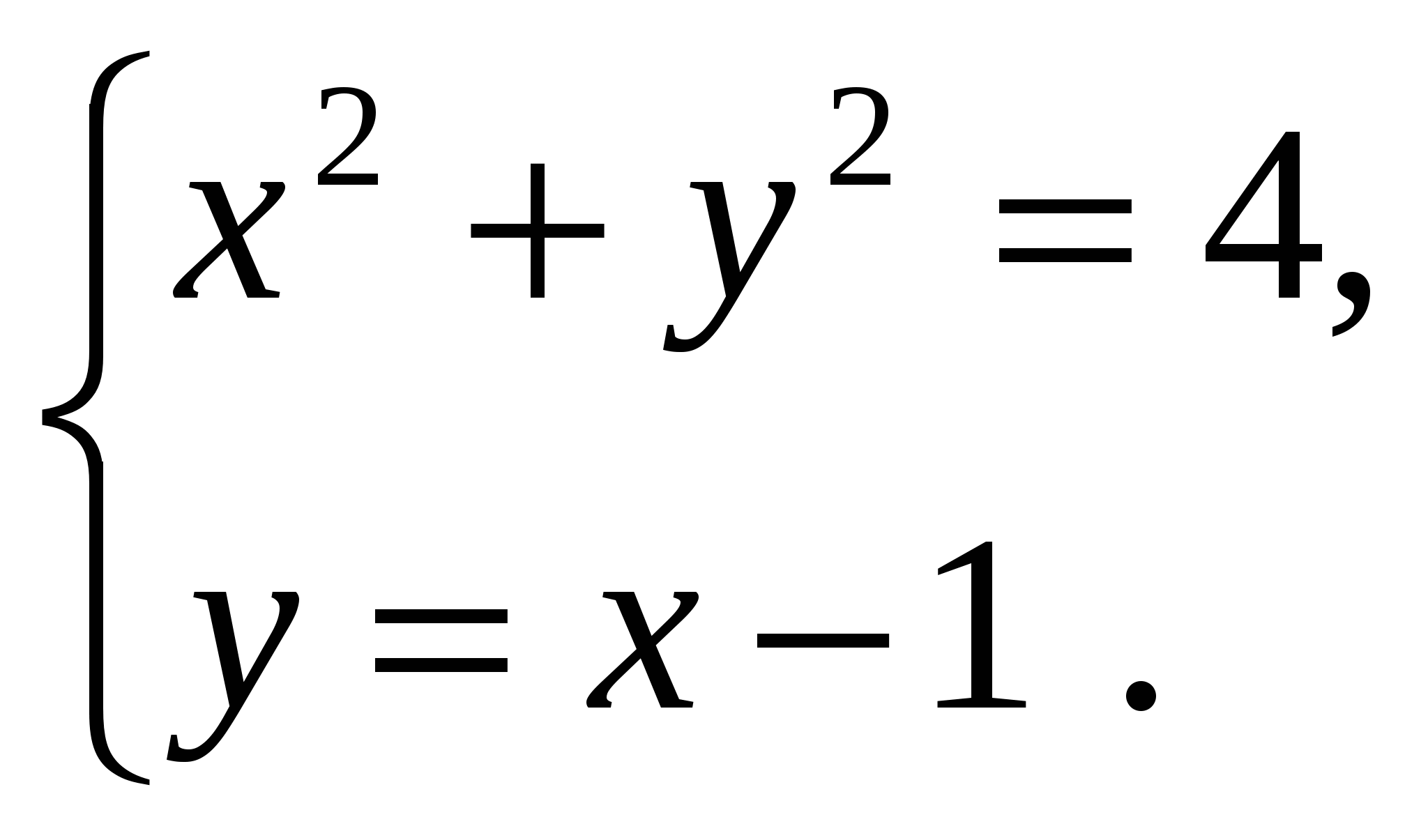г)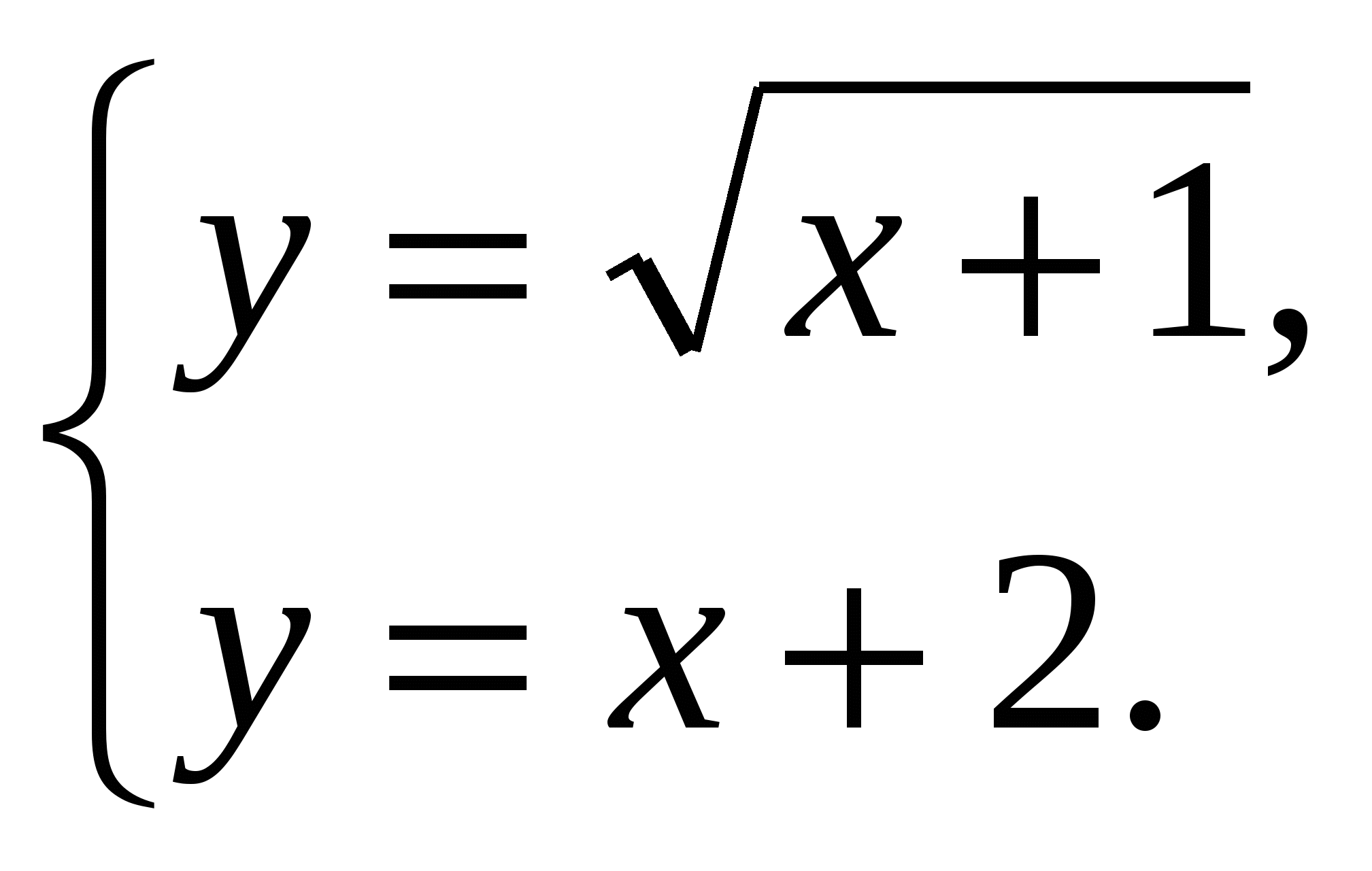

Ученики записывают решение в тетрадь, один ученик – на доске. Ответы проверяются при помощи слайда.

После выполнения задания, напомнить ученикам о выставлении самооценки в оценочный лист.

- Итак, у учеников, работающих в парах, было________________________________ Какое слово вы получили? Диофант. Чем же он так знаменит? Кто из вас слышал об этом ученом? (Далее следует рассказ ученика).

Диофант Александрийский – он жил в 3 веке нашей эры. Из работ Диофанта самой важной является “Арифметика”, из 13 книг которой только 6 сохранились до наших дней. В сохранившихся книгах Диофанта содержится 189 задач с решениями. В пяти книгах содержатся методы решения неопределенных уравнений. Это и составляет основной вклад Диофанта в математику. Что же это за уравнения?

Рассмотрим задачу на старинный сюжет. ( Текст задачи на слайде). В клетке сидят кролики и фазаны, всего у них 18 ног. Узнать, сколько в клетке тех и других. Как бы вы предложили решить эту задачу? (Обсуждение с классом.) Необходимо ввести две переменные: х – число кроликов, у – число фазанов, тогда получим уравнение 4х + 2у = 18 или 2х + у = 9. Выразим у через х: у = 9 – 2х и далее воспользуемся методом перебора: х = 1, у = 7; х = 2, у = 5; х = 3, у = 3; х = 4, у = 1. Т.о. задача имеет 4 решения.

Подобные уравнения встречаются часто, они-то и называются неопределенными. Особенность их состоит в том, что уравнение содержит две или более переменных и требуется найти все целые или натуральные их решения. Такими уравнениями и занимался Диофант. Он изобрел большое число способов решения подобных уравнений, поэтому их часто называют диофантовыми уравнениями.

2). Самостоятельная работа.

- Мы вспомнили некоторые методы решения систем уравнений. Давайте проведем небольшую самостоятельную работу. Сейчас на экране вы видите тест. С подобным тестом вы встречались при решении вариантов диагностической работы. Необходимо выбрать нужный вариант ответа. Решения и ответы записываем в свою тетрадь, сверяемся со слайдом и ставим себе балл по результатам каждой системы.

2. Исследование систем уравнений.

На данном этапе урока нам предстоит с вами побывать в роли исследователей. Перед нами стоит задача: выяснить количество решений системы двух уравнений с двумя переменными в зависимости от параметра. Задания такого типа у нас встречаются во второй части экзаменационной работы

Рассмотрим систему: ( на слайде)

- Выясним, при каких значениях а система не имеет решений, имеет одно решение, более одного решения. Рассмотрим графический способ решения.

Ученики предлагают алгоритм решения данной системы.

_______________________________________________________________________________________________________________________________________________________________________________________________________________________

Учитель показывает ход решения этой системы на слайде.

- А теперь попробуйте провести аналогичную исследовательскую работу самостоятельно, выбрав любую из понравившихся вам систем.

(Системы записаны на слайде):

Возьмите свои оценочные листы, поставьте себе оценку за работу на четвертом этапе урока.

ИТОГ урока.

Итак, сегодня мы с вами закрепили знания по теме «Решение систем уравнений с двумя переменными” различными методами. Еще раз повторим, какими? ______________________________________________________________________

Спасибо за урок, до новых встреч!