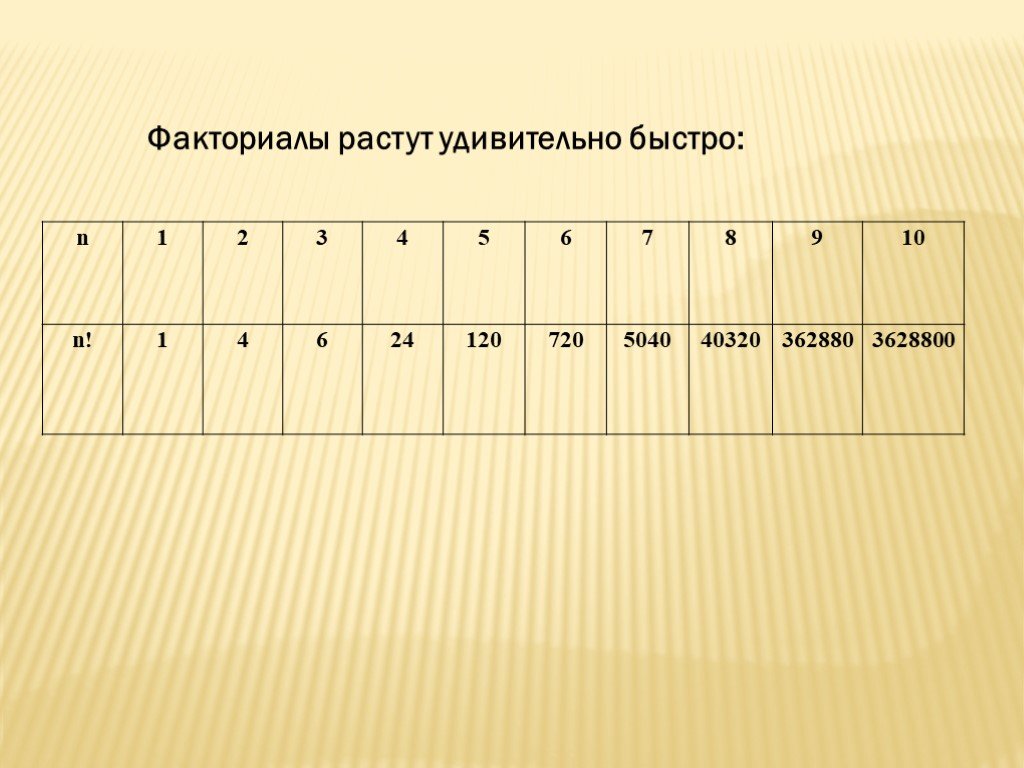
Презентация "Элементы комбинаторики: перестановки, сочетания и размещения" – проект, доклад
Презентацию на тему "Элементы комбинаторики: перестановки, сочетания и размещения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
Элементы первой группы главной подгруппы
Щелочные металлы – это элементы главной подгруппы I группы Периодической системы химических элементов Д. И. Менделеева: литий Li, натрий Na, калий ...Элементы налогообложения
По форме предоставления. По субъекту предоставления. По уровню управления. Льготные налоговые режимы. Освобождения Изъятия Вычеты Скидки. Льготы по ...Элементы v группы, главной подгруппы периодической системе элементов Д.И Менделеева
Азот (N) 2s22p3 Фосфор (P) 3s23p3 Мышьяк (As) 3d104s24p3 Сурьма (Sb) 4d105s25p3 Висмут (Bi) 4f145d106s26p3. Электронное строение:. уменьшаются. Степени ...Элементы iv группы главной подгруппыпериодической системы элементов таблицы Менделеева
Подгруппа углерода, в которую входят углерод, кремний, германий, олово и свинец, является главной подгруппой 4 группы Периодической системы. Дмитрий ...Манипуляции в общении. Элементы тренинга противостояния влиянию.
Виды влияния…как повысить эффективность взаимодействия?? Людьми гораздо легче управлять, чем их утешить и понять. Под манипуляцией понимают…. скрытое ...Искусство правильного сочетания цветов и элементов одежды
История моды. Что привело нас к тому, как мы сейчас одеваемся? Наш активный образ жизни, современные способы передвижения. Из истории известно, что ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 декабря 2018
Категория:Разные
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию