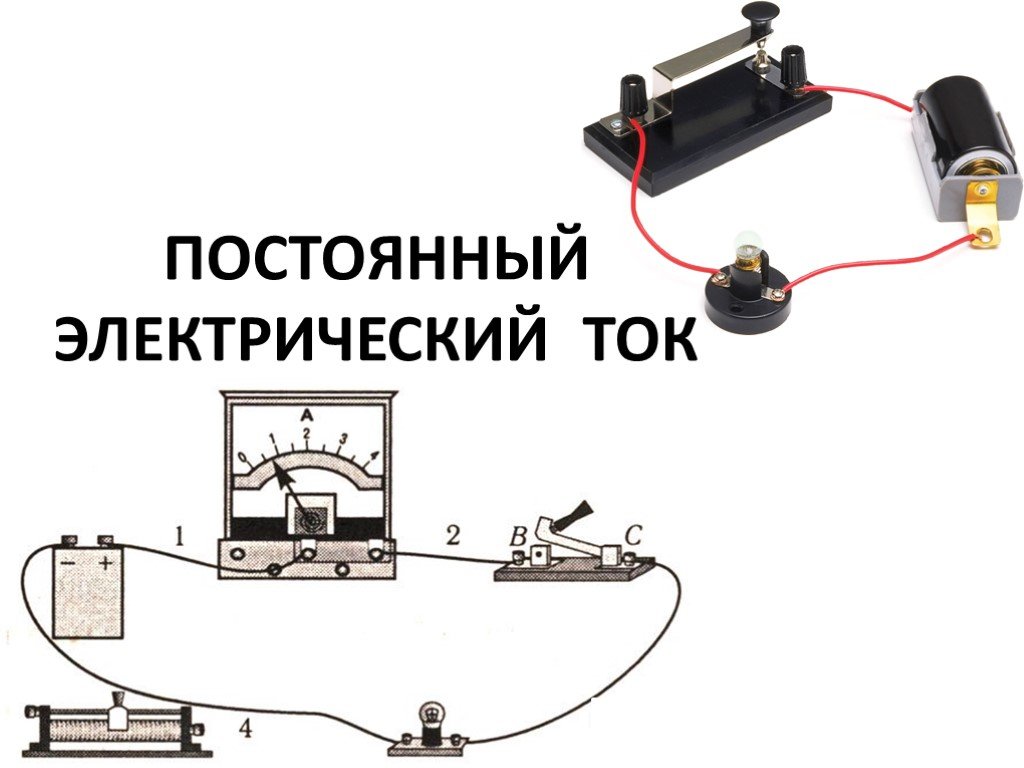
Слайд 1ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Слайд 21. Электрический ток
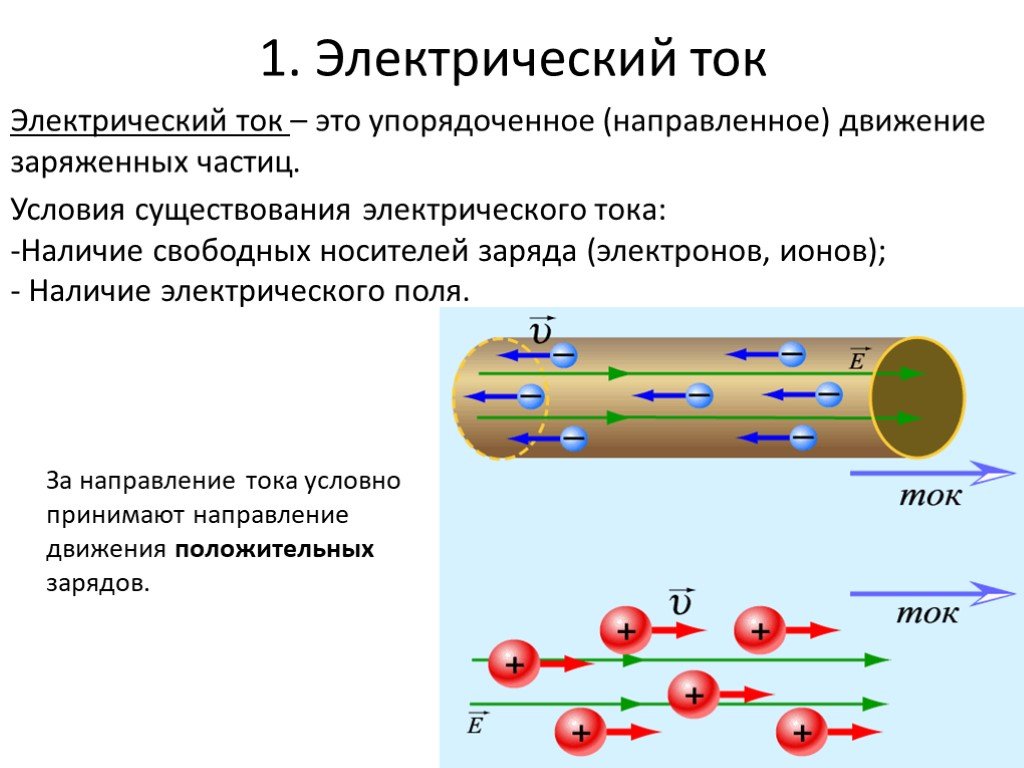
Электрический ток – это упорядоченное (направленное) движение заряженных частиц.
Условия существования электрического тока: Наличие свободных носителей заряда (электронов, ионов); - Наличие электрического поля.
За направление тока условно принимают направление движения положительных зарядов.
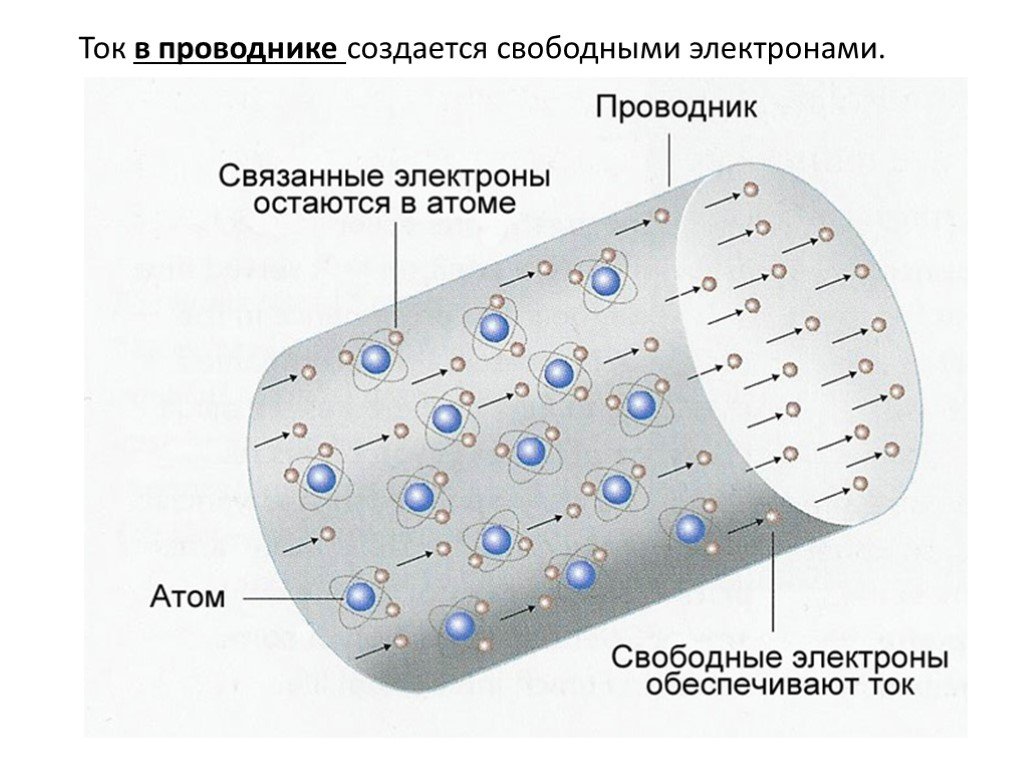
Слайд 3Ток в проводнике создается свободными электронами.
Слайд 42. Источники тока
Источники тока – устройства, способные создавать и поддерживать разность потенциалов за счет работы сил неэлектрического происхождения.
- условное обозначение источников тока
Сторонние силы – это силы неэлектрического происхождения, действующие на заряды со стороны источника тока.
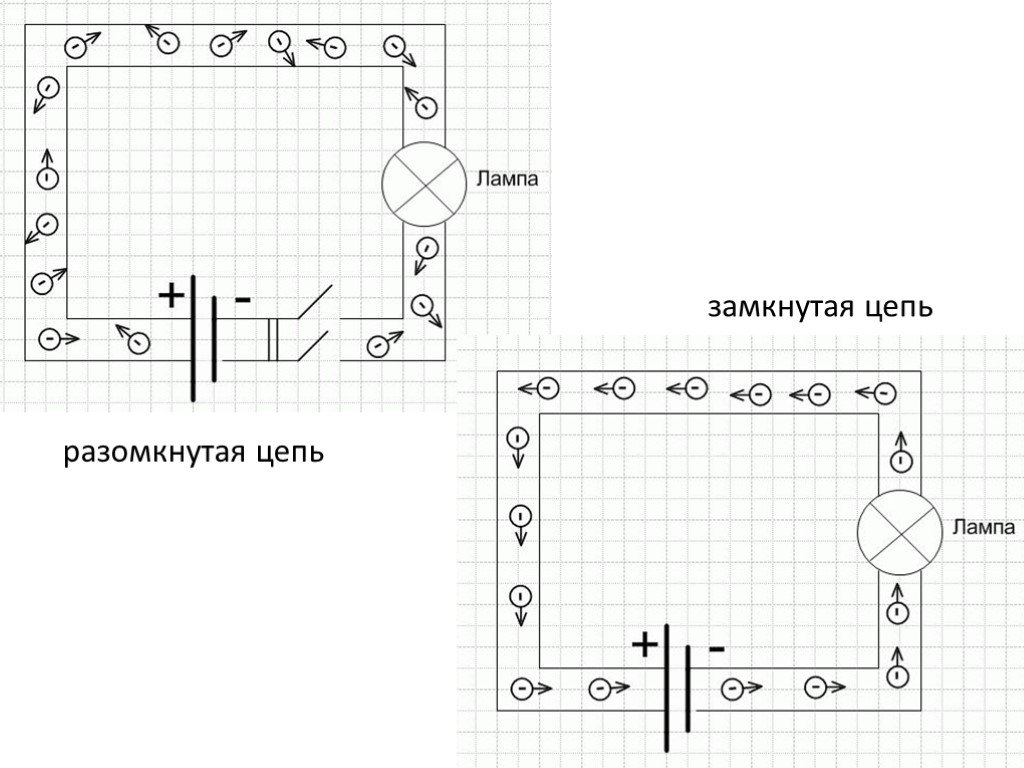
Электри́ческая цепь — совокупность устройств и элементов, предназначенных для протекания электрического тока. Для поддержания напряжения цепь должна быть замкнута на источник тока.
Слайд 5замкнутая цепь разомкнутая цепь
Слайд 6Примеры источников тока
Слайд 73. Характеристики тока
I. Сила тока.
Сила тока – это физическая величина, равная заряду, прошедшему через поперечное сечение проводника за единицу времени.
I – сила тока, [А]
dq – малый заряд, прошедший через сечение проводника за малое время dt
- определение силы тока
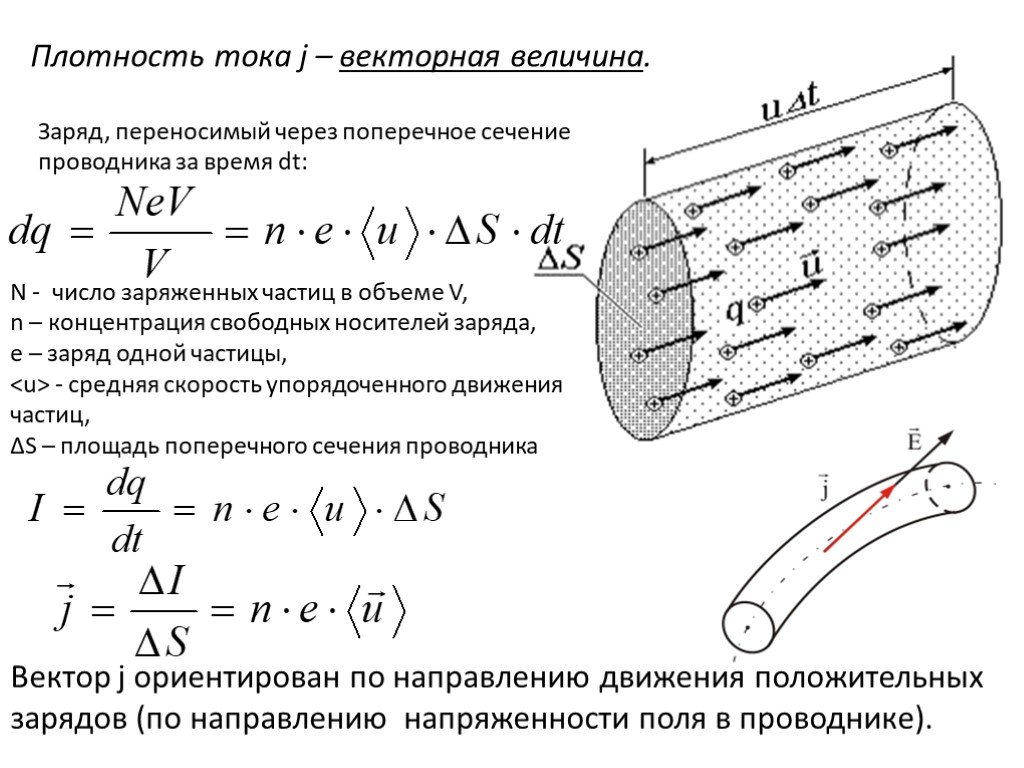
II. Плотность тока.
Плотность тока - это физическая величина, равная силе тока, прохо-дящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока.
j – плотность тока, [А/м2]
- определение плотности тока
dI – малый ток, прошедший через малое сечение проводника dS˪ , препендикулярное току.
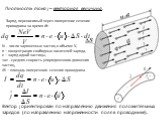
Слайд 8Плотность тока j – векторная величина.
Заряд, переносимый через поперечное сечение проводника за время dt:
N - число заряженных частиц в объеме V, n – концентрация свободных носителей заряда, е – заряд одной частицы, - средняя скорость упорядоченного движения частиц, ΔS – площадь поперечного сечения проводника
Вектор j ориентирован по направлению движения положительных зарядов (по направлению напряженности поля в проводнике).
Слайд 9III. ЭДС (электродвижущая сила).
ЭДС – это физическая величина, определяемая работой сторонних сил по перемещению единичного положительного заряда.
ε – ЭДС, [В] - определение ЭДС
Аст – работа сторонних сил по перемещению заряда q.
То есть
- ЭДС – это циркуляция вектора Е поля сторонних сил
Кроме сторонних сил на заряд действуют силы электрического поля (силы Кулона):
Результирующая сила, действующая на заряд в цепи:
Слайд 10Работа результирующей силы на участке 1-2:
IV. Напряжение.
Напряжение – это физическая величина, определяемая работой, совершаемой общим полем кулоновских и сторонних сил при перемещении единичного положительного заряда.
U – напряжение, [В]
- определение напряжения
где
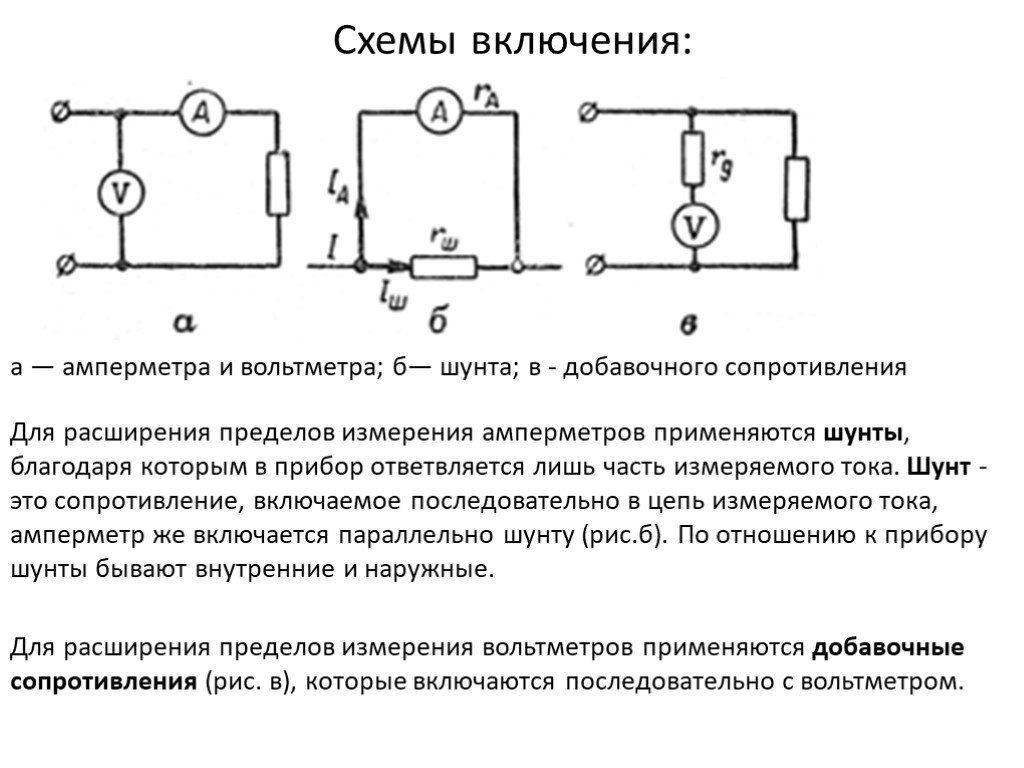
Слайд 11Амперме́тр — прибор для измерения силы тока. Включается в цепь последовательно с тем участком, на котором измеряется сила тока. Амперметр не должен изменять силу тока в цепи, поэтому его сопротивление должно быть очень малым.
Приборы для измерения силы тока и напряжения
Вольтме́тр — прибор для измерения напряжения и ЭДС. Включается в цепь параллельно тому участку, на котором измеряется напряжение. Сопротивление вольтметра должно быть очень большим. Для измерения ЭДС вольтметр включается параллельно источнику тока при разомкнутой цепи.

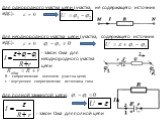
Слайд 12Схемы включения:
а — амперметра и вольтметра; б— шунта; в - добавочного сопротивления
Для расширения пределов измерения амперметров применяются шунты, благодаря которым в прибор ответвляется лишь часть измеряемого тока. Шунт - это сопротивление, включаемое последовательно в цепь измеряемого тока, амперметр же включается параллельно шунту (рис.б). По отношению к прибору шунты бывают внутренние и наружные.
Для расширения пределов измерения вольтметров применяются добавочные сопротивления (рис. в), которые включаются последовательно с вольтметром.
Слайд 13V. Сопротивление.
Сопротивление – это физическая величина, характеризующая способность вещества проводить электрический ток.
R – сопротивление, [Ом]
- определение сопротивления
ρ – удельное сопротивление проводника (характеристика материала), [Ом·м]; L – длина проводника; S – площадь поперечного сечения проводника.
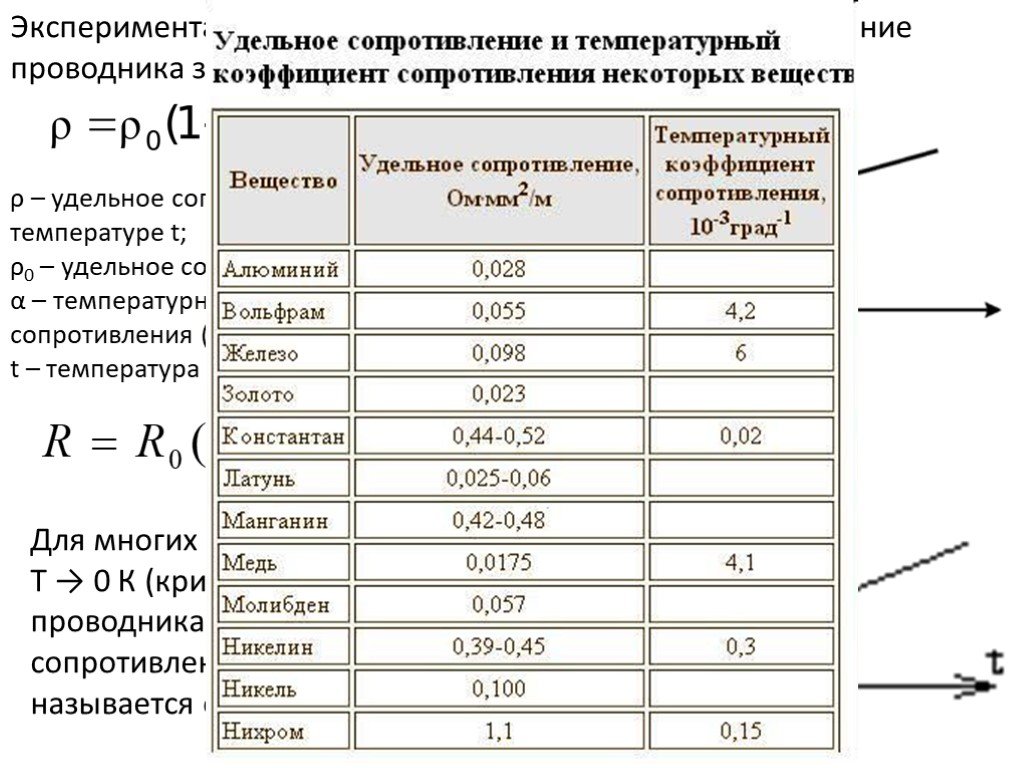
Слайд 14Экспериментально установлено, что удельное сопротивление проводника зависит от температуры.
ρ – удельное сопротивление при температуре t; ρ0 – удельное сопротивление при t = 0 0С; α – температурный коэффициент сопротивления (характеристика материала); t – температура в 0С.
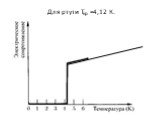
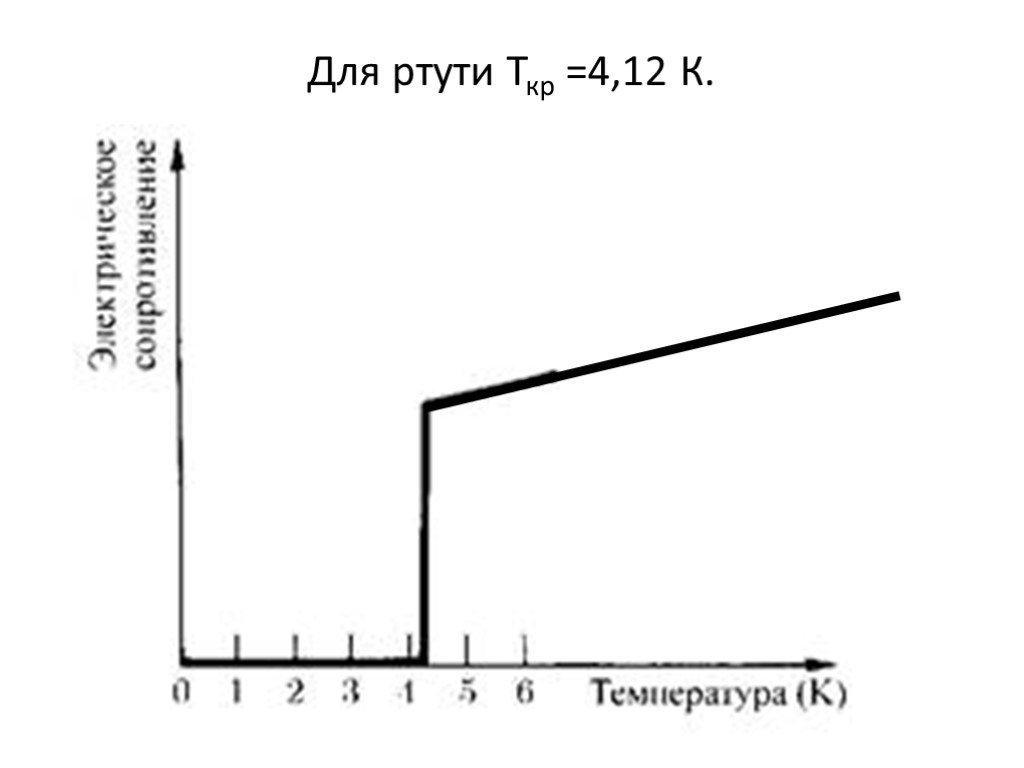
Для многих металлов и сплавов при T → 0 К (критической температуре) у проводника резко исчезает сопротивление. Такое явление называется сверхпроводимость.
Слайд 15Для ртути Ткр =4,12 К.
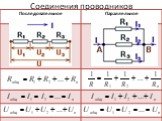
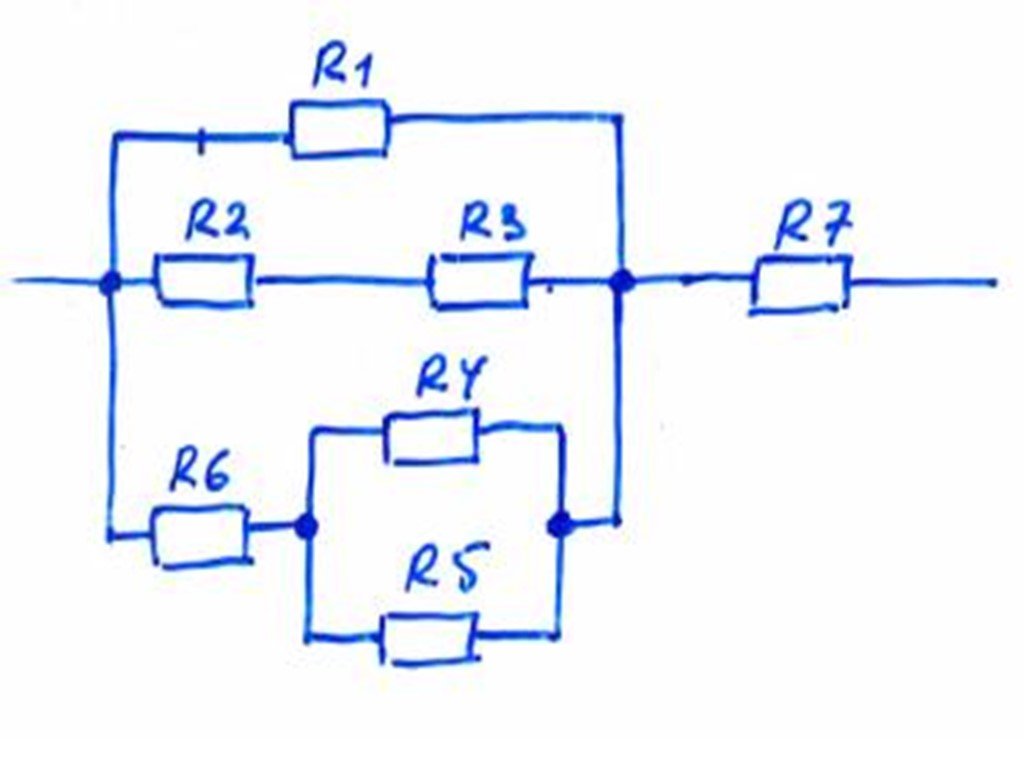
Слайд 16Соединения проводников
Слайд 17
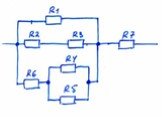
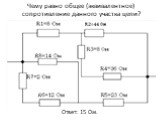
Слайд 18Чему равно общее (эквивалентное) сопротивление данного участка цепи?
Ответ: 15 Ом.
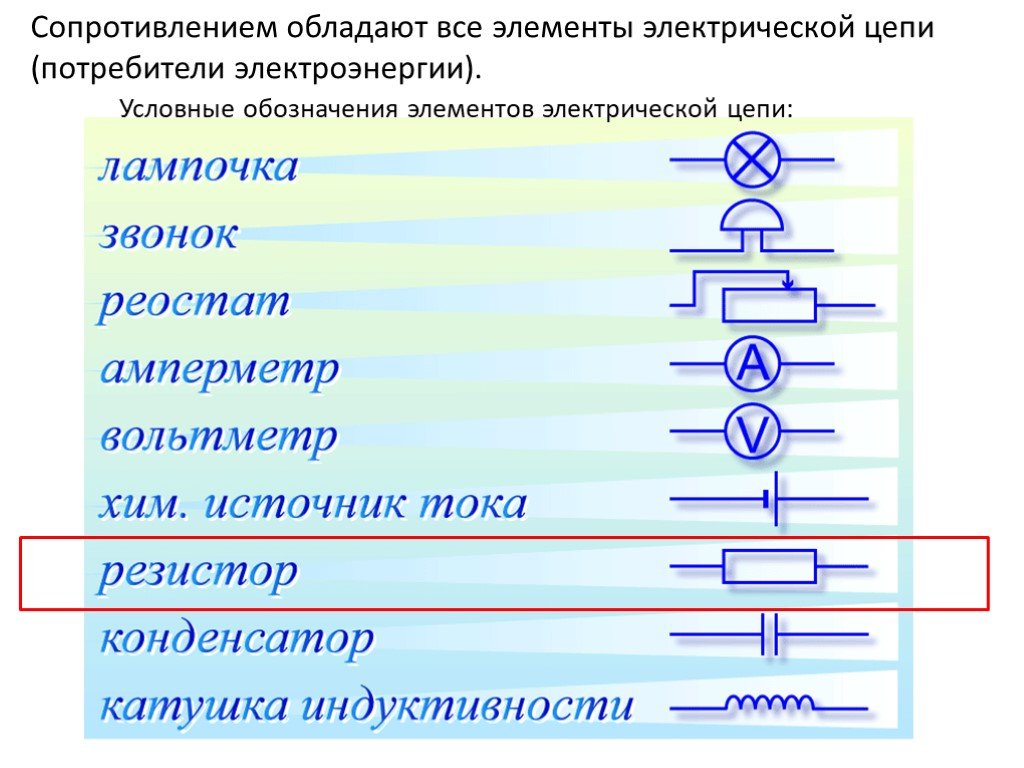
Слайд 19Сопротивлением обладают все элементы электрической цепи (потребители электроэнергии).
Условные обозначения элементов электрической цепи:
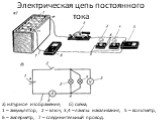
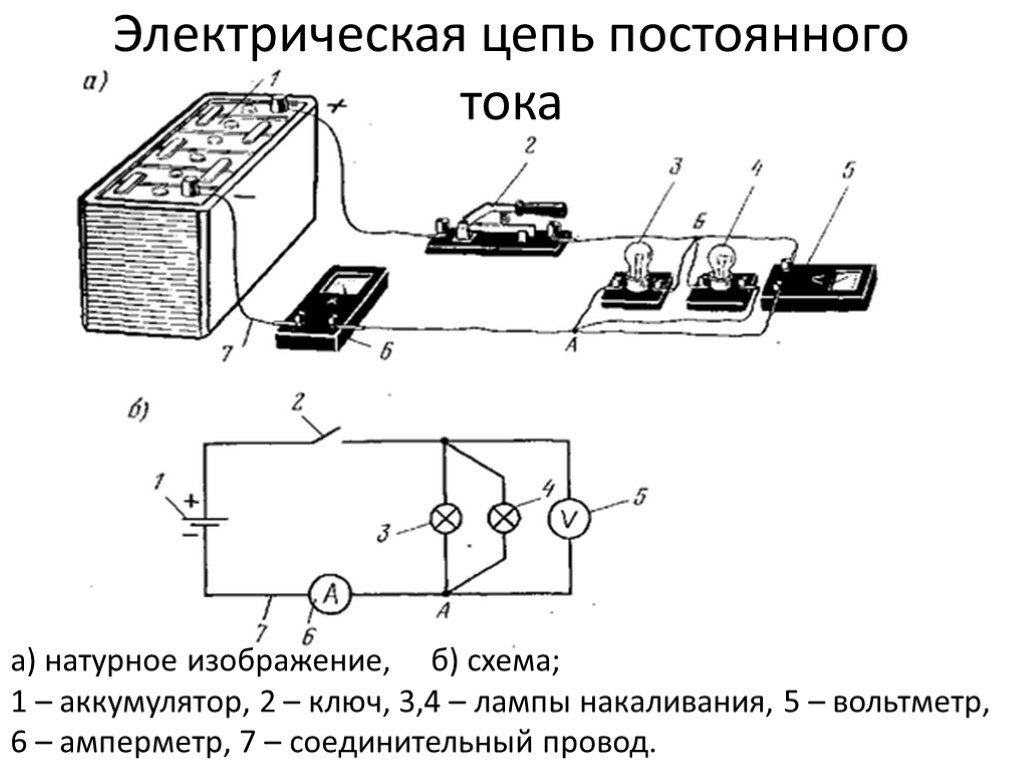
Слайд 20Электрическая цепь постоянного тока
а) натурное изображение, б) схема; 1 – аккумулятор, 2 – ключ, 3,4 – лампы накаливания, 5 – вольтметр, 6 – амперметр, 7 – соединительный провод.
Слайд 214. Закон Ома
Георг Симон Ом 1787 - 1854
Ом экспериментально установил, что сила тока, текущего по однородному металлическому проводнику прямо пропорциональна напряжению U и обратно пропорциональна сопротивлению R проводника.
- закон Ома для постоянных полей
Где
- удельная проводимость проводника, [См/м]
- закон Ома в дифференциальной форме для любых полей
j – плотность тока в произвольной точке проводника, Е – напряженность эл. поля в той же точке
Слайд 22Для однородного участка цепи (участка, не содержащего источник ЭДС):
Для неоднородного участка цепи (участка, содержащего источник ЭДС):
Для полной замкнутой цепи:
- закон Ома для полной цепи
R – сопротивление внешнего участка цепи; r – внутреннее сопротивление источника тока
- закон Ома для неоднородного участка цепи
2
Слайд 23Короткое замыкание
Соединение проводов «накоротко», т.е. когда внешнее сопротивление R = 0.
Соединение, не предусмотренное конструкцией и нарушающее нормальную работу устройства.
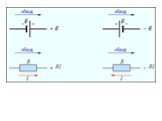
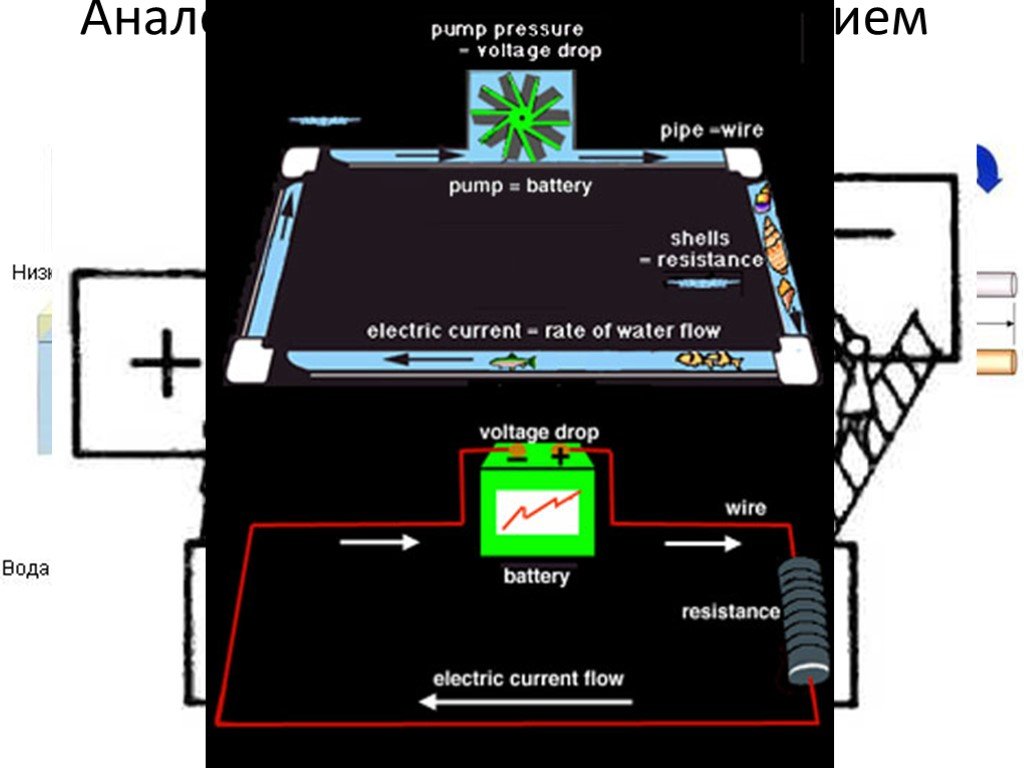
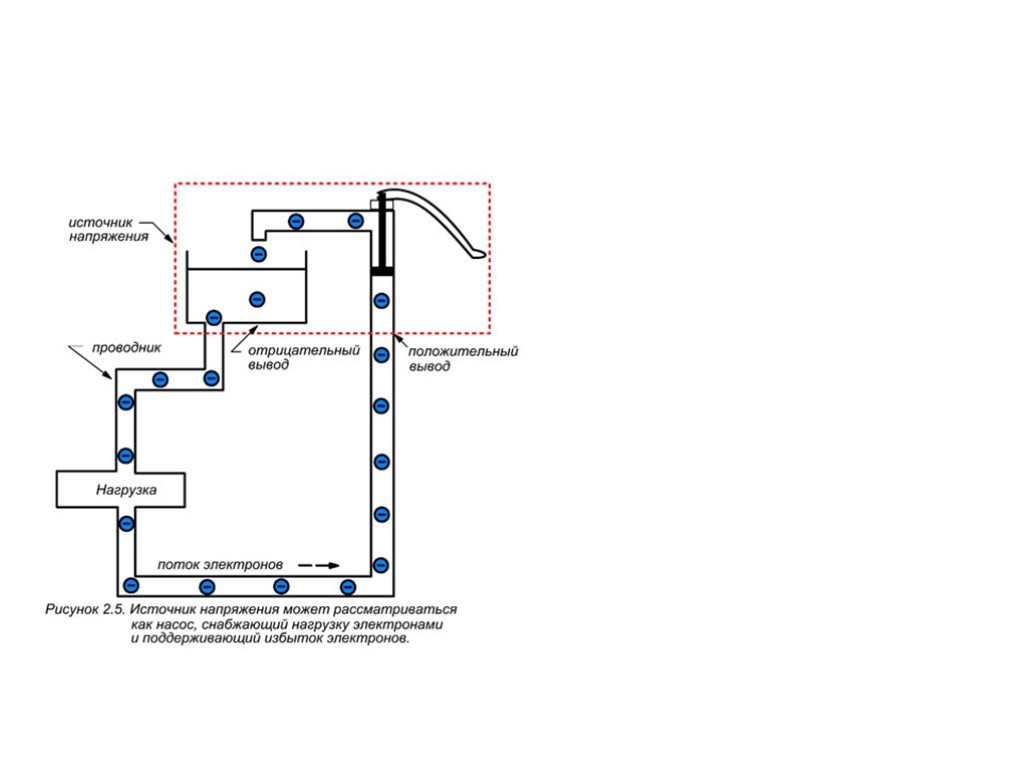
Слайд 24Аналогия между током и течением жидкости
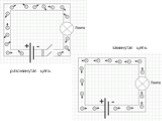
Слайд 25Механическая модель электрической цепи
Слайд 26
Слайд 275. Правила Кирхгофа для разветвленных цепей
Густав Кирхгоф 1824 - 1887
Разветвленные цепи – это цепи, содержащие несколько замкнутых контуров, которые могут иметь общие участки, и несколько источников тока.
(Правила Кирхгофа вытекают из законов Ома).
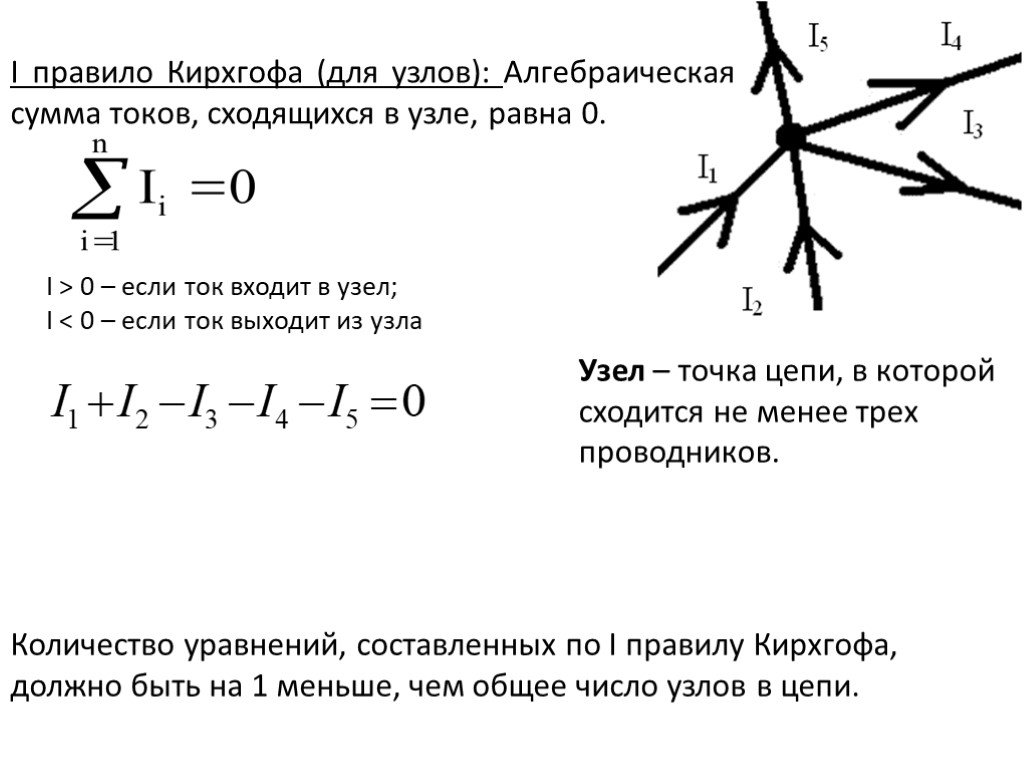
Слайд 28I правило Кирхгофа (для узлов): Алгебраическая сумма токов, сходящихся в узле, равна 0.
Узел – точка цепи, в которой сходится не менее трех проводников.
I > 0 – если ток входит в узел; I < 0 – если ток выходит из узла
Количество уравнений, составленных по I правилу Кирхгофа, должно быть на 1 меньше, чем общее число узлов в цепи.
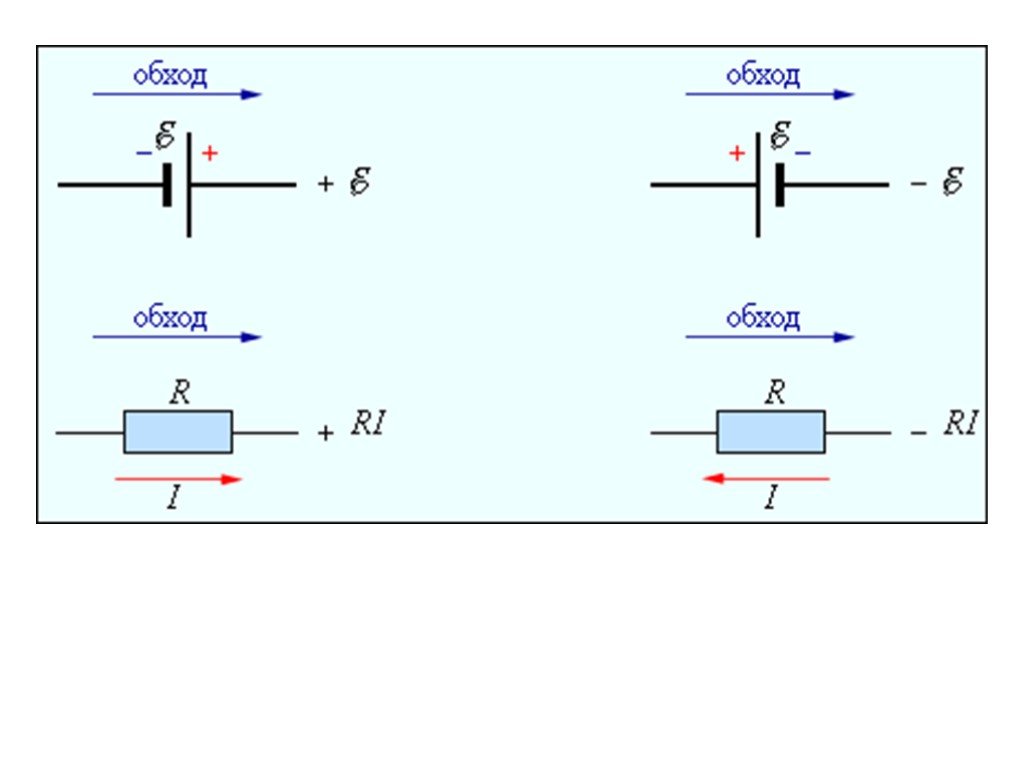
Слайд 29II правило Кирхгофа (для замкнутых контуров): Алгебраическая сумма напряжений на участках замкнутого контура равна алгебраической сумме ЭДС, встречающихся в данном контуре.
За положительное направление обхода обычно принимается направление по часовой стрелке.
- если ток на участке совпадает с направлением обхода;
- если ток на участке НЕ совпадает с направлением обхода;
- если ЭДС действует по выбранному направлению обхода.
Общее количество уравнений, составленных по I и II правилам Кирхгофа, должно равняться количеству неизвестных в цепи. В систему должны входить все сопротивления и ЭДС рассматриваемой цепи.
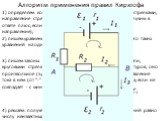
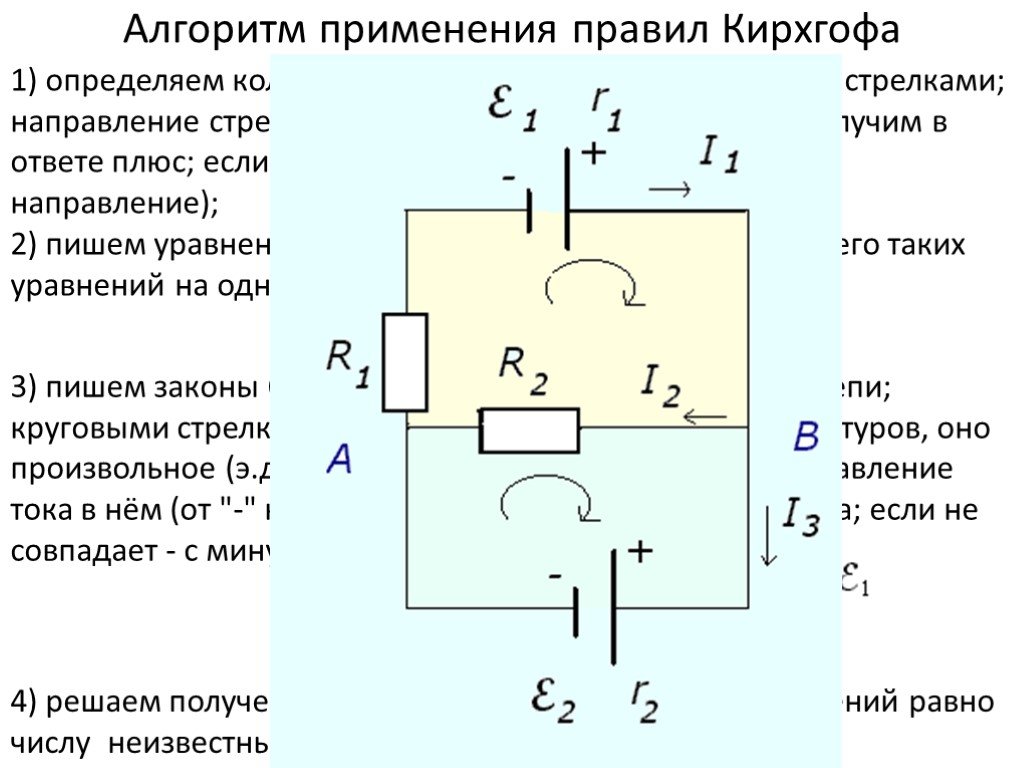
Слайд 30Алгоритм применения правил Кирхгофа
1) определяем количество токов в цепи и обозначаем их стрелками; направление стрелок - произвольное (если отгадаем, получим в ответе плюс; если нет - минус, то есть противоположное направление); 2) пишем уравнение неразрывности для нашего узла (всего таких уравнений на одно меньше количества узлов):
3) пишем законы Ома для разных замкнутых контуров цепи; круговыми стрелками показано направление обхода контуров, оно произвольное (э.д.с. берётся со знаком плюс, если направление тока в нём (от "-" к "+") совпадает с направлением обхода; если не совпадает - с минусом):
4) решаем полученную систему уравнений (число уравнений равно числу неизвестных).
Слайд 31
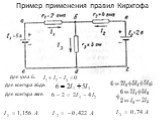
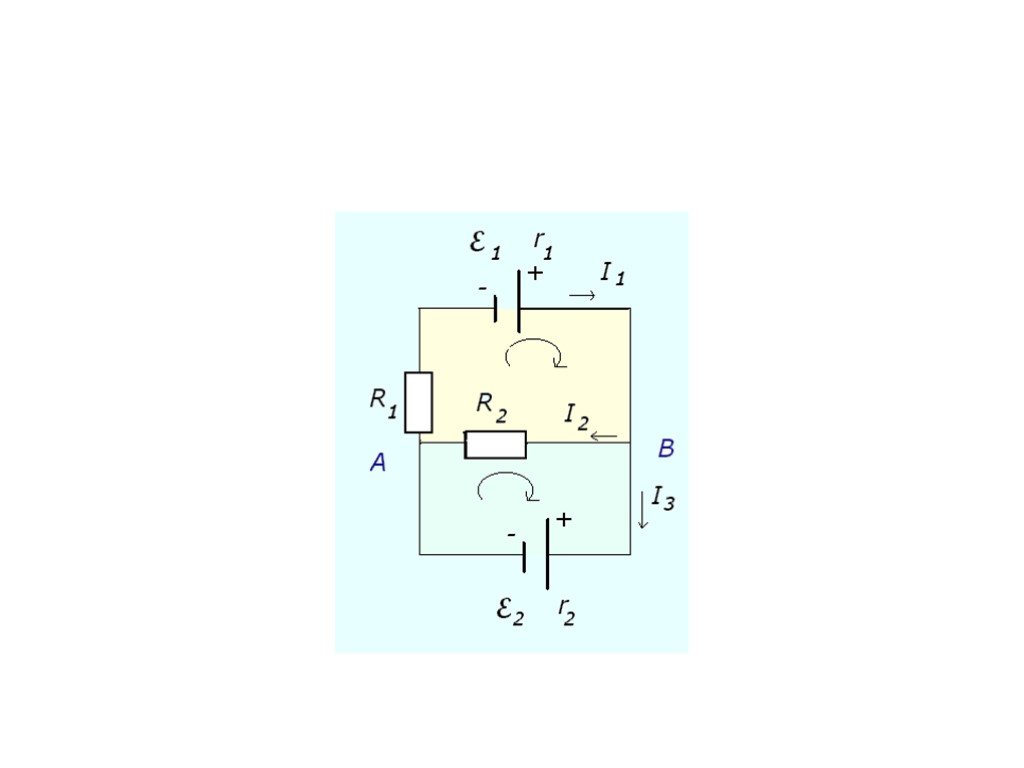
Слайд 32Пример применения правил Кирхгофа
Для контура абде: Для узла б: Для контура авге:
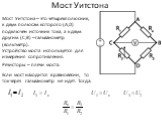
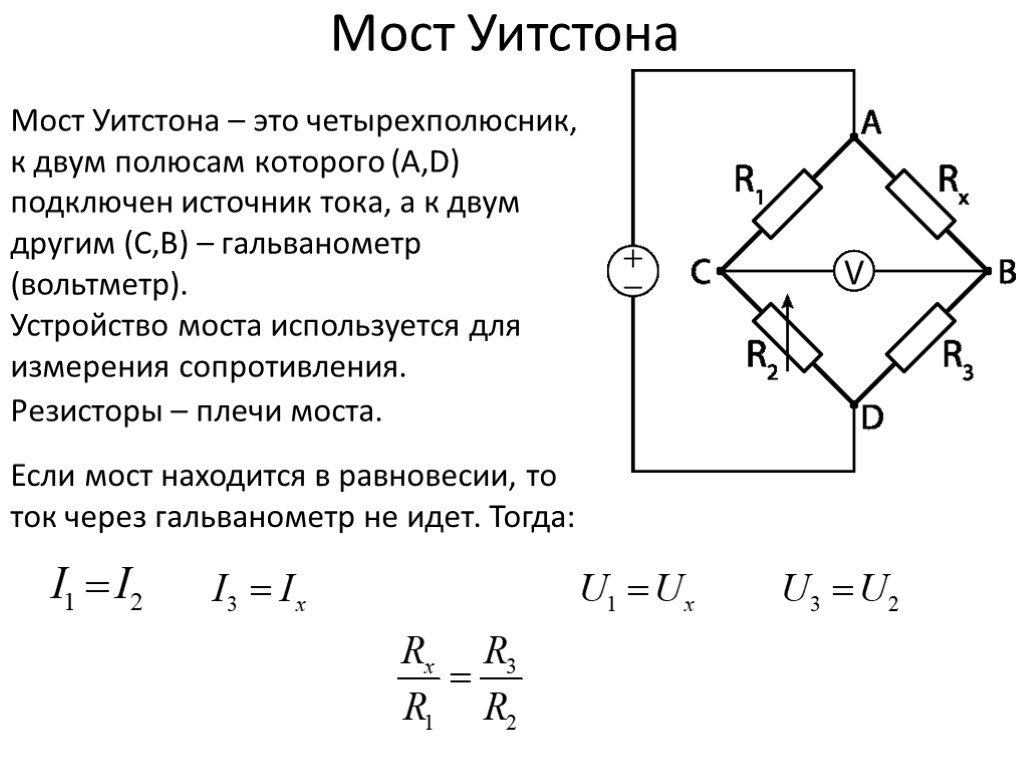
Слайд 33Мост Уитстона
Мост Уитстона – это четырехполюсник, к двум полюсам которого (A,D) подключен источник тока, а к двум другим (C,B) – гальванометр (вольтметр). Устройство моста используется для измерения сопротивления.
Резисторы – плечи моста.
Если мост находится в равновесии, то ток через гальванометр не идет. Тогда:
Слайд 34
Слайд 35
Слайд 36
























![3. Характеристики тока. I. Сила тока. Сила тока – это физическая величина, равная заряду, прошедшему через поперечное сечение проводника за единицу времени. I – сила тока, [А]. dq – малый заряд, прошедший через сечение проводника за малое время dt. - определение силы тока. II. Плотность тока. Плотно 3. Характеристики тока. I. Сила тока. Сила тока – это физическая величина, равная заряду, прошедшему через поперечное сечение проводника за единицу времени. I – сила тока, [А]. dq – малый заряд, прошедший через сечение проводника за малое время dt. - определение силы тока. II. Плотность тока. Плотно](https://prezentacii.org/upload/cloud/19/06/151448/images/thumbs/screen7.jpg)

![III. ЭДС (электродвижущая сила). ЭДС – это физическая величина, определяемая работой сторонних сил по перемещению единичного положительного заряда. ε – ЭДС, [В] - определение ЭДС. Аст – работа сторонних сил по перемещению заряда q. То есть. - ЭДС – это циркуляция вектора Е поля сторонних сил. Кроме III. ЭДС (электродвижущая сила). ЭДС – это физическая величина, определяемая работой сторонних сил по перемещению единичного положительного заряда. ε – ЭДС, [В] - определение ЭДС. Аст – работа сторонних сил по перемещению заряда q. То есть. - ЭДС – это циркуляция вектора Е поля сторонних сил. Кроме](https://prezentacii.org/upload/cloud/19/06/151448/images/thumbs/screen9.jpg)
![Работа результирующей силы на участке 1-2: IV. Напряжение. Напряжение – это физическая величина, определяемая работой, совершаемой общим полем кулоновских и сторонних сил при перемещении единичного положительного заряда. U – напряжение, [В]. - определение напряжения. где Работа результирующей силы на участке 1-2: IV. Напряжение. Напряжение – это физическая величина, определяемая работой, совершаемой общим полем кулоновских и сторонних сил при перемещении единичного положительного заряда. U – напряжение, [В]. - определение напряжения. где](https://prezentacii.org/upload/cloud/19/06/151448/images/thumbs/screen10.jpg)


![V. Сопротивление. Сопротивление – это физическая величина, характеризующая способность вещества проводить электрический ток. R – сопротивление, [Ом]. - определение сопротивления. ρ – удельное сопротивление проводника (характеристика материала), [Ом·м]; L – длина проводника; S – площадь поперечного с V. Сопротивление. Сопротивление – это физическая величина, характеризующая способность вещества проводить электрический ток. R – сопротивление, [Ом]. - определение сопротивления. ρ – удельное сопротивление проводника (характеристика материала), [Ом·м]; L – длина проводника; S – площадь поперечного с](https://prezentacii.org/upload/cloud/19/06/151448/images/thumbs/screen13.jpg)