Презентация "Выборочный метод в исследовании" – проект, доклад

Выборочный метод в исследовании

Банных Г.А. К.с.н., доцент

ОСИ Банных Г.А.

Ангус Дитон

- восхождение от частного к общему - Почти идеальная система спроса - Парадокс Дитона - изучение «счастья»

Исследования сплошные и выборочные

Что такое сплошные и выборочные исследования? Понятие о генеральной совокупности Все субъекты, подходящие для проведения исследования Самая большая генеральная совокупность – все человечество Понятие выборки - Sample

Генеральная совокупность и выборка

Генеральная совокупность – это полная совокупность единиц ( вся статистическая совокупность). Выборочная совокупность (выборка) - это часть единиц генеральной совокупности, отобранная в случайном порядке. Обозначения: объем генеральной совокупности – N; объем выборки - n

Генеральная совокупность

Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и времени.

Почему?

Почему исследователи любят выборочные исследования

Меньше работы Меньше денег Меньше времени Меньше головной боли (?)

Допущение

Результаты, полученные на выборке, можно распространить на всю генеральную совокупность (с известным допущением, выражаемым через вероятности ά- и β-ошибок)

Оптимальный размер выборки

В интересах исследователя В интересах реально существующей ситуации в генеральной совокупности

Выборка (Выборочная cовокупность)

- Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности. - Отобранное по строго заданному правилу число элементов генеральной совокупности, подлежащее непосредственному исследованию. Единицы анализа – элементы выбранной, или обследуемой совокупности. Ими могут быть как индивиды, так и, например, учебные группы, бригады и т.д. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности.

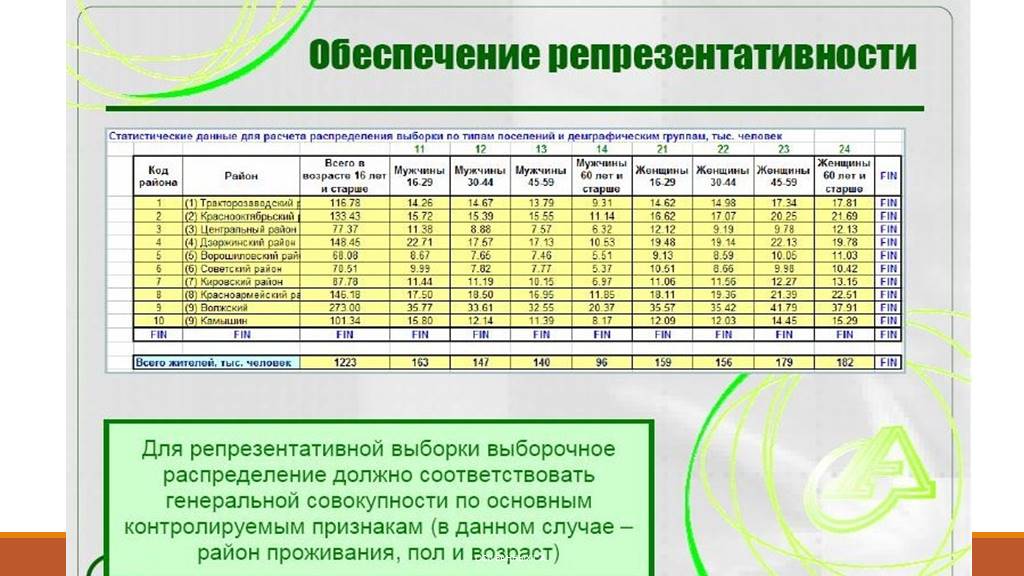
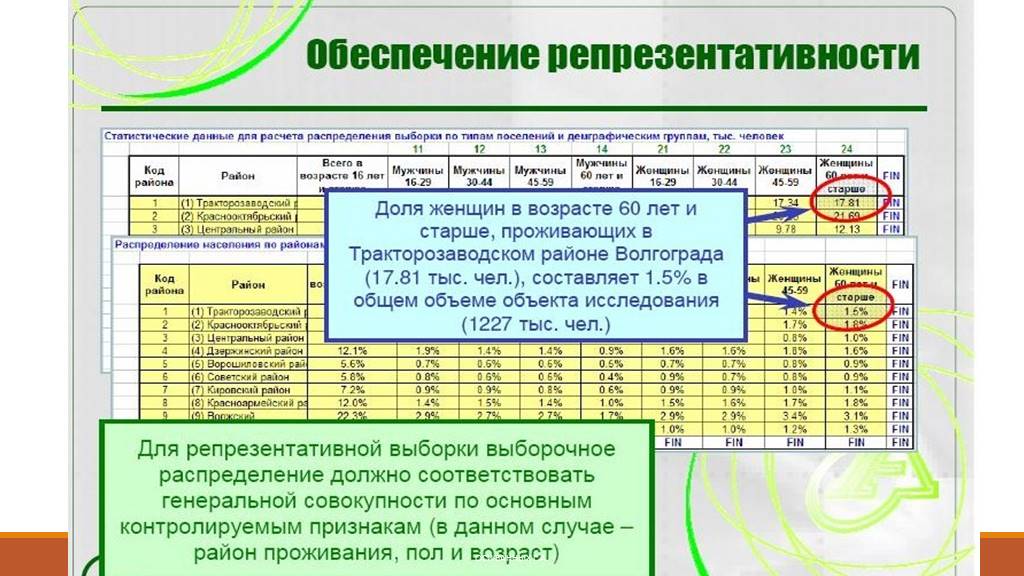
Репрезентативность выборки

Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей.

Ошибки репрезентативности

(представительности) возникают в результате того, что состав отобранной для обследования части единиц совокупности недостаточно полно отображает состав всей изучаемой совокупности (иначе говоря не все типы явления представлены в выборке).

РЕПРЕЗЕНТАТИВНОСТЬ И ОШИБКА ВЫБОРКИ

В то же время, Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от ошибки никак не зависит от размера выборки.

Ошибка выборки (доверительный интервал)

Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности.

Статистическая ошибка

Систематическая ошибка

Зависит от размера выборки. Чем больше размер выборки, тем она ниже.

зависит от различных факторов, оказывающих постоянное воздействие на исследование и смещающих результаты исследования в определенную сторону.

Систематические ошибки

= неконтролируемые перекосы в распределении выборочных наблюдений («потеря» объекта). При возрастании объема выборки не уменьшаются 1936 г. выборы президента (Рузвельт – Лэндон): «Литерэри Дайджест»: 2 376 523 человека  Прогноз: Лендон – 57% , Рузвельт – 43%. Результат: Рузвельт – 62,5%, Лэндон – 37,5%

George Gallup (1901 – 1984)

Типичные систематические ошибки

Давление доступных объектов Иллюзия постоянства (пренебрежение группой неопределившихся респондентов) Недостаточный учет аномальных и труднодоступных единиц исследования (больные, личный состав ВС…) Недостаточный учет отсутствующих в месте сбора данных (нет дома) Отказы от ответа (нет мнения, негативная установка, внешние обстоятельства)

Ошибка выборки

- это погрешность, с которой выборочные данные могут быть перенесены на всю аудиторию. Обычно ошибка выборки не превышает 5% на 95% доверительном интервале. .

Средняя ошибка выборки

Средняя ошибка выборки () – это среднее (по выборкам) отклонение выборочной оценки от истинного значения генеральной характеристики. В каждой конкретной выборке фактическая ошибка выборки может быть меньше средней ошибки, равна ей или больше ее. Причем каждое из этих расхождений имеет различную вероятность.

Предельная ошибка выборки

Предельная ошибка выборки () – это максимально возможная при данной вероятности ошибка выборки. То есть мы с заданной вероятностью (Рдов) гарантируем, что оценка ,полученная по нашей конкретной выборке, будет отличаться от значения генеральной характеристики не больше, чем на величину предельной ошибки .

Доверительная вероятность

Вероятность, с которой мы гарантируем, что ошибка нашей выборки не превысит предельную ошибку, называется доверительной вероятностью - Рдов. Предельная ошибка рассчитывается по формуле: =t·, где t- коэффициент доверия, значение которого определяется доверительной вероятностью (Рдов). Чем больше Рдов, тем больше t.

Понятие об ά- и β-ошибке

Результаты тестирования нулевой гипотезы

Истинноот рицательные

ά-ошибка нет β-ошибка

Истинноположительные

да

Результат проверки истинности нулевой гипотезы

Нулевая гипотеза истинна

ά- и β-ошибки в выборочном исследовании

Вероятность ошибки – P value, величина p. Какую величину p мы можем допустить? pά

Величина pά для выборки

Величина p

Закон больших чисел

– методологическая основа выборочного метода. Теоретической основой выборочного метода является закон больших чисел: С увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются (т.е. чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Вопросы, предваряющие процедуру выборки

Как сделать репрезентативную выборку? или Как избежать ошибки отбора selection bias и Насколько я готов ошибиться исходя из того, что обследована будет не генеральная совокупность а выборка из нее?

Объем выборки – общее число единиц наблюдения, включенных в выборочную совокупность

Чем больше объем выборки – тем выше точность ее результатов Чем более однородна генеральная совокупность – тем меньший объем выборки можно использовать Однородная совокупность – в которой контролируемый признак распределен равномерно (не образует пустот и сгущений) Объем выборки зависит от: целей и задач, гипотез и методов исследования; объема ГС; степени однородности ГС; требующейся точности полученной информации характера предполагаемых распределений ответа…;

Стратегии расчета объема выборки

предварительная – объем выборки определяется до проведения основного исследования; последовательная – объем выборки не рассчитывается заранее, а ставится в зависимость от конечных результатов исследования (например, в телефонном опросе постоянно проводится расчет распределений ответов на все вопросы и требуемого объема выборки); комбинированная – предварительно рассчитывают верхние допустимые значения для последовательной стратегии.

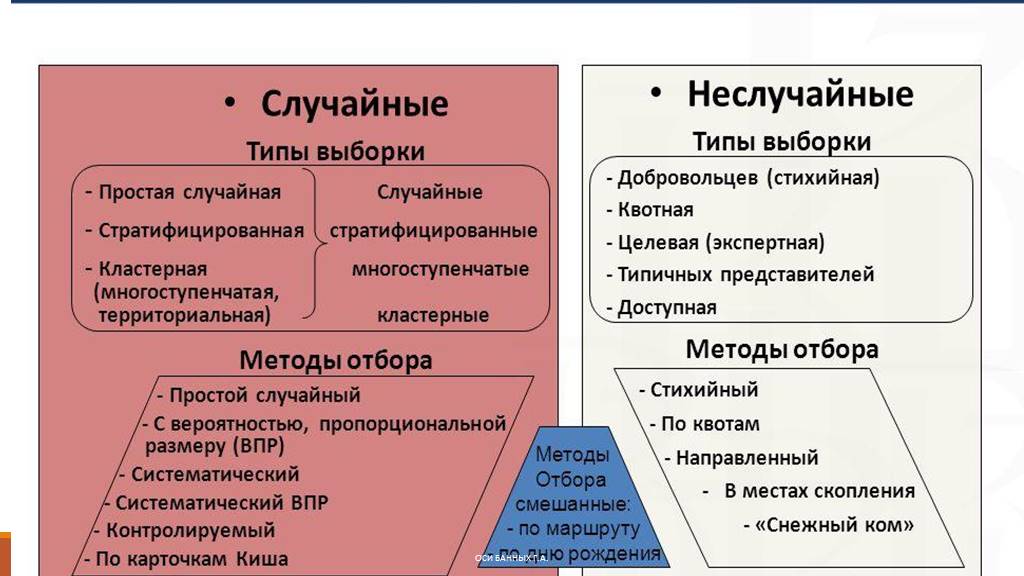
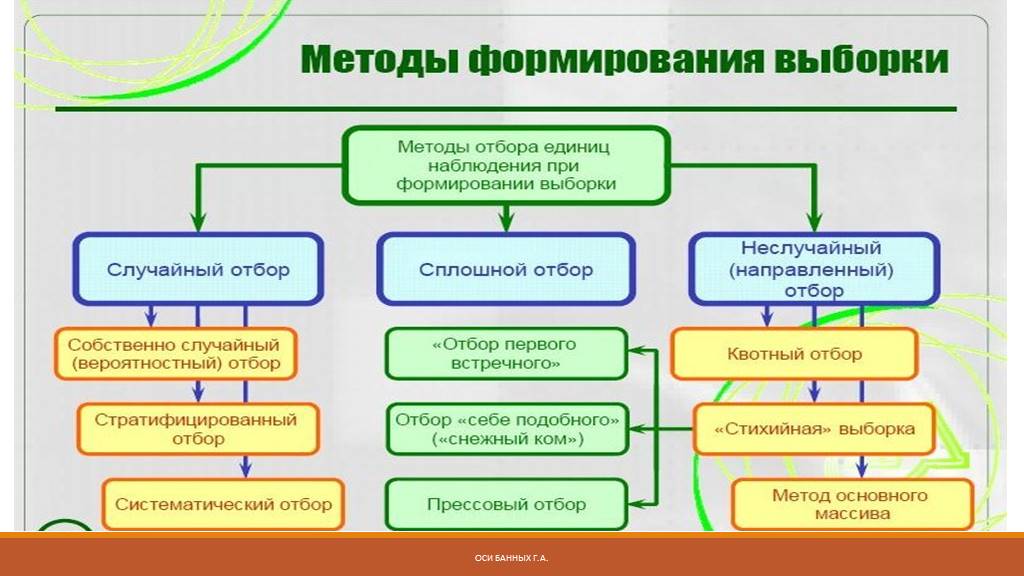
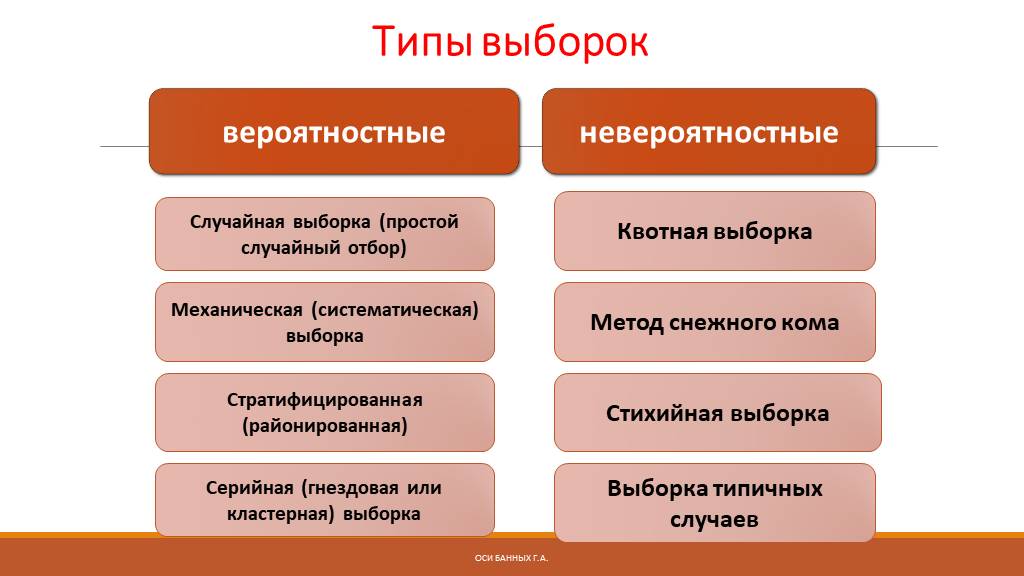
Типы выборок вероятностные невероятностные

Случайная выборка (простой случайный отбор)

Механическая (систематическая) выборка

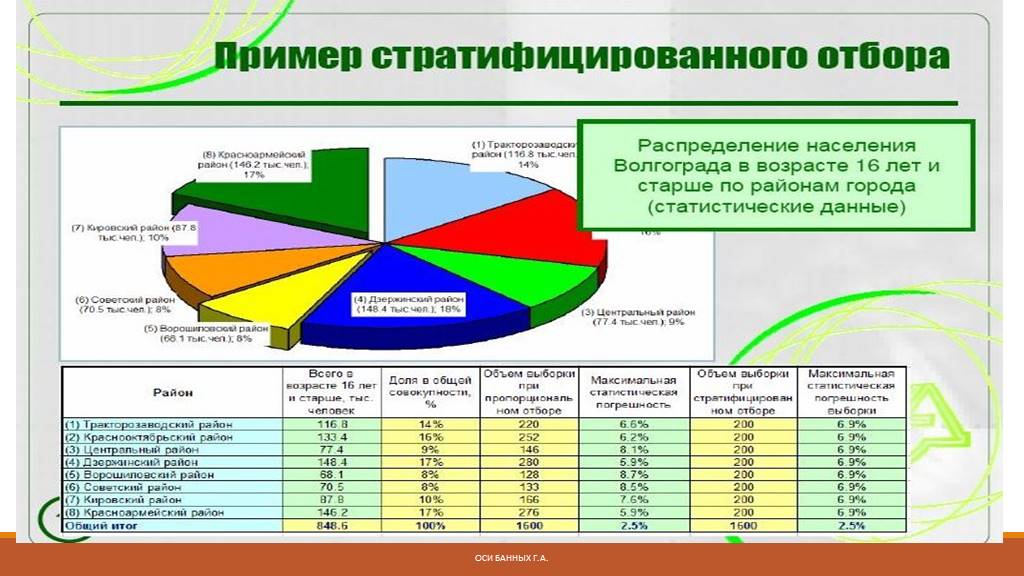
Стратифицированная (районированная)

Серийная (гнездовая или кластерная) выборка

Квотная выборка

Метод снежного кома

Стихийная выборка

Выборка типичных случаев

Простая случайная выборка

Жребий Кубики Генератор случайных чисел Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов, наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел.

Кластерная выборка

Классы школы Цеха завода Дома микрорайона

Стратифицированная выборка

Выборка соответствует генеральной совокупности по структуре Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы (страты). В каждой страте отбор осуществляется случайным или механическим образом.

Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер генеральной совокупности, при этом – N=n*k

Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60 лет; лица с доходом до 13 тысяч , с доходом от 13 до 30 тысяч и с доходом свыше 30 тысяч) Для каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки используются в исследованиях достаточно часто.

Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов.

У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.)

Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает проблема выбора признака и определения его типичного значения.

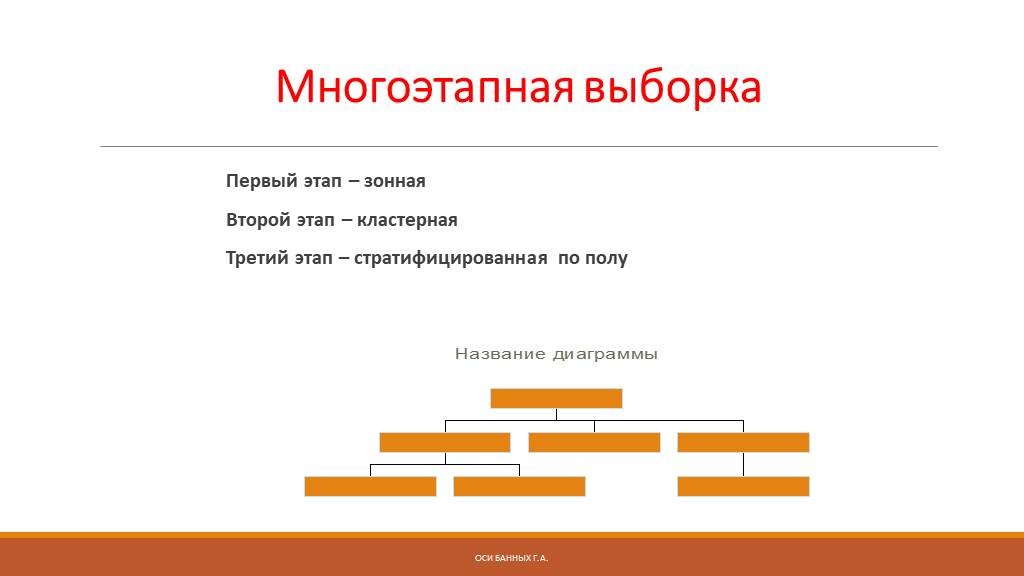
Многоэтапная выборка

Первый этап – зонная Второй этап – кластерная Третий этап – стратифицированная по полу

Обоснование системы выборки единиц наблюдения

Метод основного массива – опрос 60-70% генеральной совокупности. Если опрос проводится в рамках коллектива, представительным (репрезентативным) будет сплошное анкетирование. В масштабах организации следует опросить 25%. При массовых опросах (генеральная совокупность в пределах 5000 чел.) достаточной является 10%-я выборка.

Стратегия предварительного расчета (случайная выборка)

Необходимо знать: Желаемую точность оценивания (5%) Величину риска получаемого ответа (0,95) Степень изменчивости ответа (50% на 50% при дихотомическом вопросе, т.е. макс. разброс берем, если нет информации о распределении ответов на вопрос)

Зависимость объема выборки от распределения дихотомического ответа

10% ?

Расчет квотной выборки

1 вариант – как для случайной (при больших объемах) (см. таблицу выше) 2 вариант – на основе теории малых выборок (если не предполагается анализ по группам): количество градаций вопросов х 25 (минимальный статистически значимый размер группы): Например: пол (2 градации); возраст (2 градации: до 30, после 30); удовлетворенность трудом (5-балльная шкала) V выборки = 2х2х5х25 = 500 человек

Стратегия последовательного расчета выборки

Объем выборки не рассчитывается заранее – а ставится в зависимости от результатов исследования: в зависимости от разброса оценок  необходимый V выборки Зависимость объема выборки от коэффициента вариации (= ср.квадр.отклонение от ср.арифм. в %)

* Удобна – если можно производить необходимые расчеты в ходе самого опроса

Комбинированная стратегия

Рассчитываем выборку по предварительной стратегии  получаем верхние допустимые значения для последовательной стратегии (т.е. ту величину объема, при которой опрос прекращается)

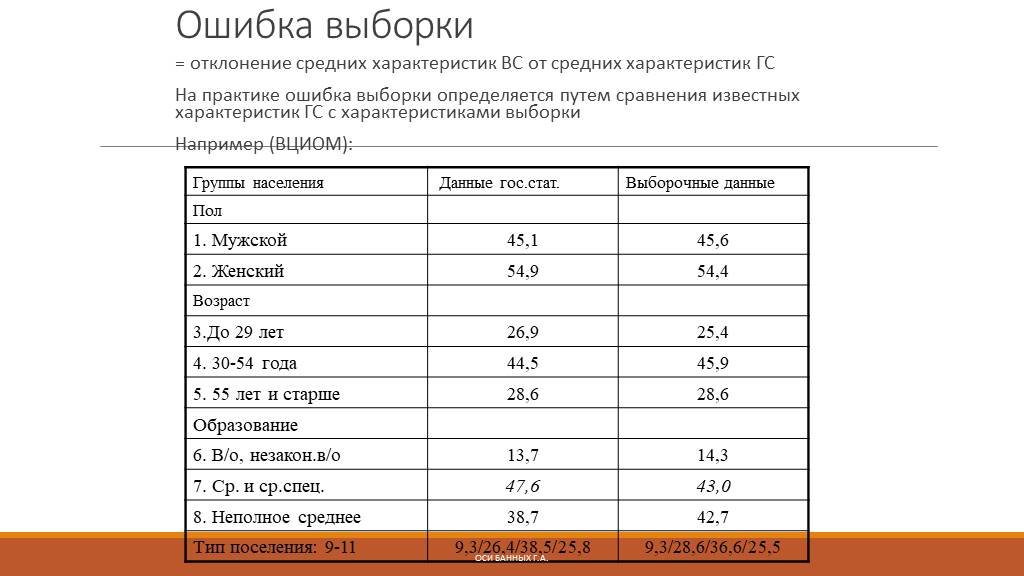
= отклонение средних характеристик ВС от средних характеристик ГС На практике ошибка выборки определяется путем сравнения известных характеристик ГС с характеристиками выборки Например (ВЦИОМ):

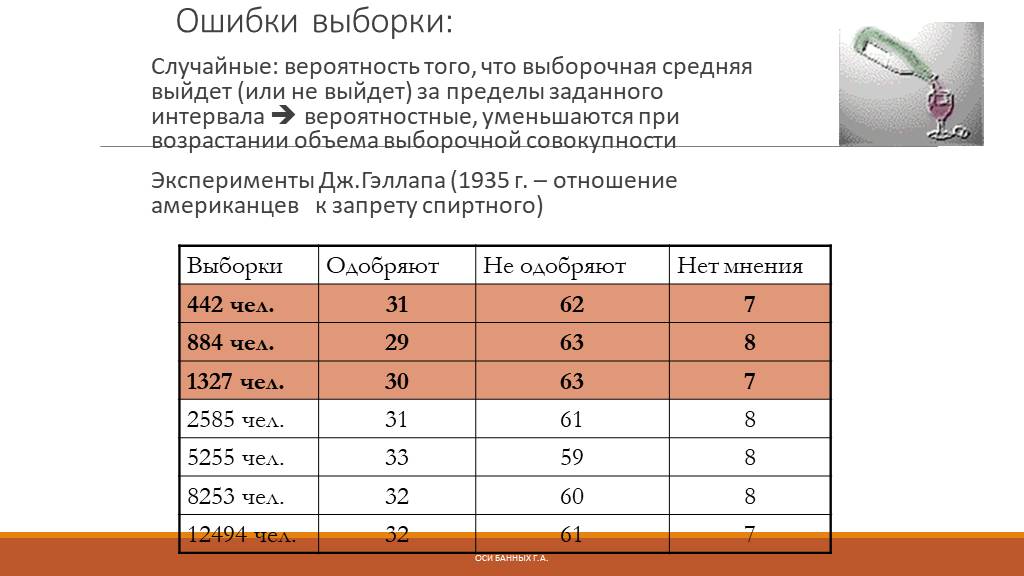
Ошибки выборки:

Случайные: вероятность того, что выборочная средняя выйдет (или не выйдет) за пределы заданного интервала  вероятностные, уменьшаются при возрастании объема выборочной совокупности Эксперименты Дж.Гэллапа (1935 г. – отношение американцев к запрету спиртного)

Порядок определения выборочной совокупности

Проектирование выборки включает: Определение границ и состава генеральной совокупности (сплошное или выборочное исследование). Определение типа выборки (случайная, квотная, гнездовая, простая или многоcтупенчатая). Определение объема выборки. Расчет предельной ошибки выборки (репрезентативности). Определение технологии отбора объектов. Репрезентативность (представительность) – свойство выборки отражать характеристики генеральной совокупности. Формулы для определения объема выборки: где n – объем выборочной совокупности, N – объем генеральной совокупности, t2 – число, определяемое по специальным таблицам с учетом предельной ошибки выборки и доверительной вероятности, A – предельная ошибка выборки. Выборка считается репрезентативной, если она отражает характеристики генеральной совокупности не ниже, чем на 95%.

n = (0,25 t2 N ) / (A2N+0,25t2),

Контроль и ремонт выборки

Ремонт В. = процесс устранения погрешностей, т.е. расхождения ВС и ГС различными способами: Коррекция ВС (напр., формирование повторной выборки или выборки большего размера, или следующих номер абонента…) Коррекция распределений демографических характеристик респондентов (взвешивание исходных данных…) Коррекция резко выделяющихся ответов респондентов (брак?) Коррекция пропущенных ответов

СПАСИБО ЗА ВНИМАНИЕ!