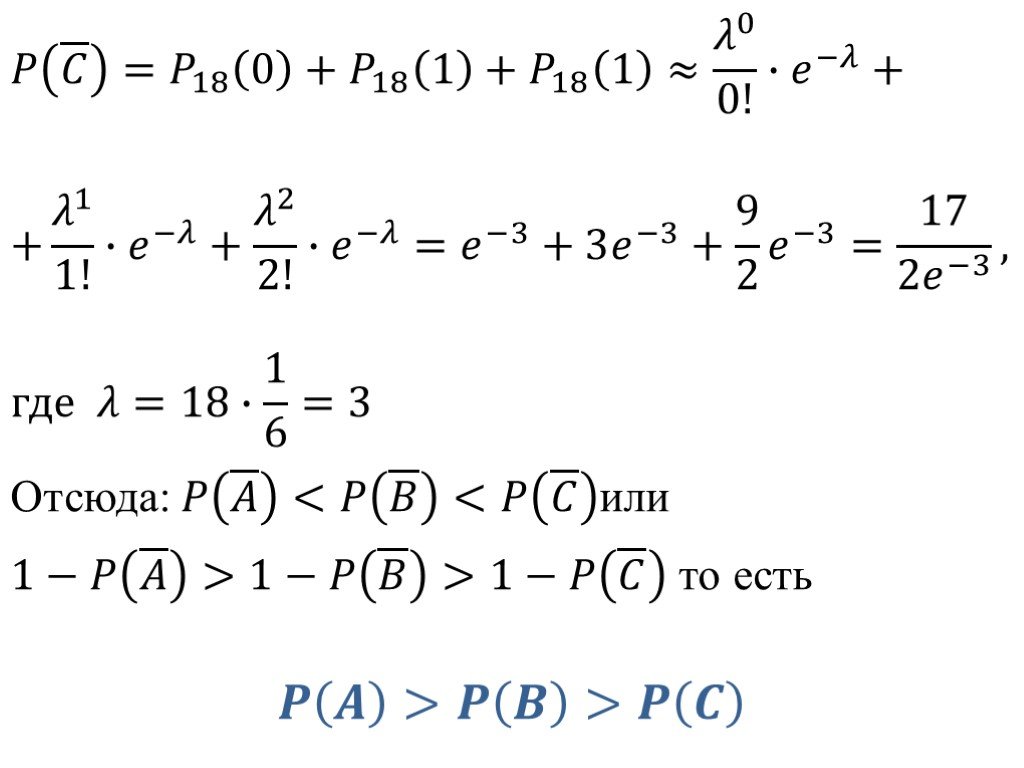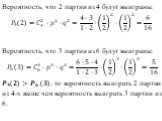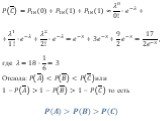Презентация "Повторение независимых испытанийСХЕМА БЕРНУЛЛИ" – проект, доклад

Повторение независимых испытаний СХЕМА БЕРНУЛЛИ

Рассмотрим случай, когда одно и то же испытание повторяется несколько раз - проводится серия испытаний в одинаковых условиях, т. е. вероятность появления события А во всех опытах одна и та же (const). Такие испытания называются повторными независимыми. В задачах определим вероятность появления события А k раз (любое заданное количество раз), в серии из n опытов.

Примеры независимых испытаний 1. Несколько последовательных бросаний монеты. 2. Несколько последовательных выниманий карты из колоды, при условии, что карта возвращается каждый раз и колода перемешивается, т.е. выборка с возвращением (иначе испытания –зависимые). 3. Несколько последовательных бросаний игральной кости…

Пусть в результате случайного испытания может произойти или не произойти событие А. Если событие наступило, назовём испытание успешным, а событие – успехом. Испытание повторяется n раз. При этом соблюдаются условия: вероятность успеха P(A) = p в каждом испытании одна и та же; результат любого испытания не зависит от исходов предыдущих.

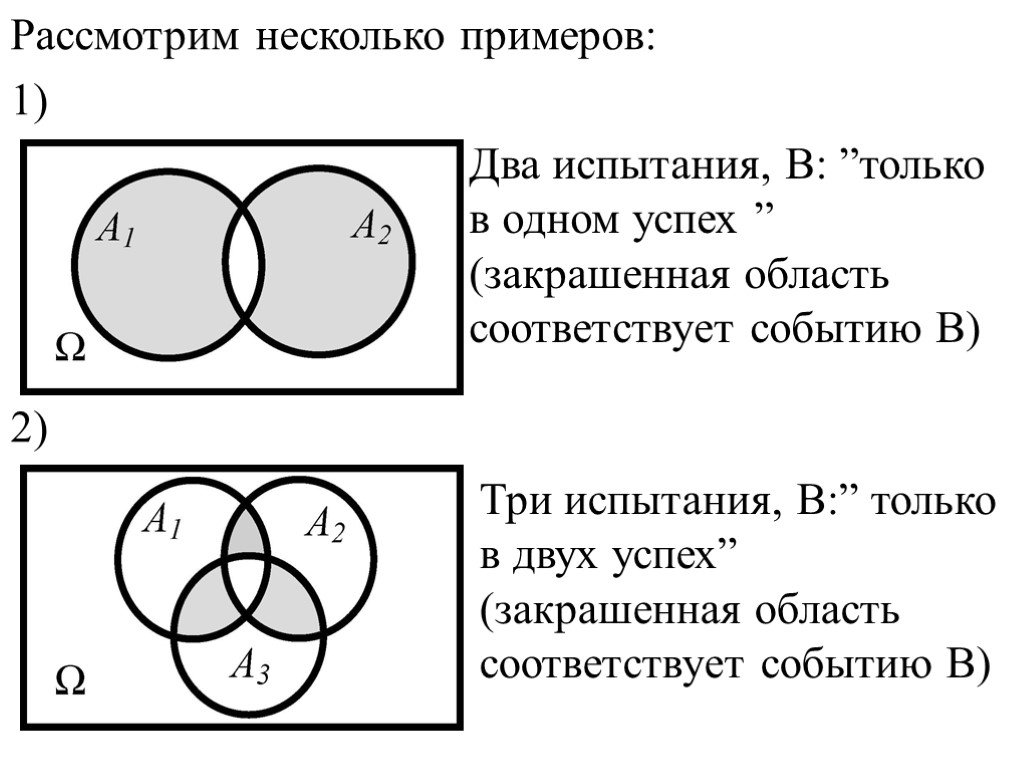
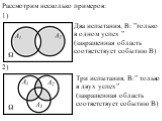
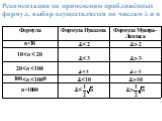
Рассмотрим несколько примеров: 1) 2)

Рассмотрим событие Bm, состоящее в том, что событие Aв этих nиспытаниях наступит ровноm раз и не наступит ровно(n - m)раз. Обозначим Ai (i=1,2,…,n) появление событияA, ? ? -непоявлениеA в i–м испытании. В силу постоянства условий испытания: P(A1) = P(A2) = …= P(An) = p P( ? ? ) = P( ? ? ) = …= P( ? ? ) = 1 - p = q Aможет появитьсяm раз в разных комбинациях, чередуясь с противоположным ? .

Число возможных комбинаций равно числу сочетаний изn элементов по m, т. е. ? ? ? . Следовательно, событиеBm можно представить в виде суммы сложных несовместных событий, причем число слагаемых равно ? ? ? : Bm= A1A2…Am ? ?+1 … ? ? +… …+ ? 1 ? 2 … ? ?−? An – m +1…An где в каждое произведение Aвходит mраз, ? - (n – m)раз. Вероятность каждого сложного события формулы по т. умножения вероятностей независимых событий равна ? ? ? ?−? .

Так как общее количество таких событий ? ? ? , топо т. сложения вероятностей несовместных событий вероятность события Bm(об. Pm(n)): P n(m)= ? ? ? ·? ? ? ?−? или Pn (m)= ?! ?! ?−? ! ·? ? ? ?−? Формулу называют формулой Бернулли, а повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятностей наз. схемой (испытаниями) Бернулли.

Пример.Игральная кость брошена 6 раз. Найти вероятность, что ровно 3 раза выпадет «шестёрка». Решение. Шестикратное бросание кости можно рассматривать как последовательность независимых испытаний с вероятностью успеха («шестерки») 1/6, и вероятностью неудачи — 5/6. Искомую вероятность вычисляем по формуле: ? ? ? = ? 6 (3)= ? 6 3 · 1 6 3 5 6 3 =0,053

Пример. Игральная кость брошена 4 раза. Найти вероятность, что «6» появится не более 2-х раз. Решение: Пусть событие В - шестерка появится не более двух раз. В является суммой несовместных событий: В0 – шестерка не появится ни разу; В1 – появится 1 раз; В2 – появится 2 раза. Произведенное испытание – бросание игральной кости. Событие А (успех) – выпадение «6». Событие А (неудача) – выпадение любого числа очков, кроме «6».

По классическому определению вероятности: Таких испытаний по условию производится 4. Тогда вероятность, что в 4-х независимых испытаниях будет 0 успехов: Аналогично:

Используя т. сложения несовместных событий: Рассмотрим следующий пример, когда из двух очень похожих вопросов на один можно ответить, пользуясь формулой Бернулли, а для другого этой формулы оказывается недостаточно.

Пример. Система радиолокационных станций ведет наблюдение за группой объектов, состоящей из 8 единиц. Каждый объект может быть (независимо от других) потерян с вероятностью 0,1. Найти вероятность того, что хотя бы один из объектов будет потерян. Решение: Пусть событие А = {потерять системой радиолокационных станций хотя бы один объект}, тогда: Р(А) = Р8(1) + Р8(2) + ... + P8(8) .

Проще найти вероятность противоположного события - ни один объект не потерян. ? ? = ? 8 0 =? 8 0 ∙ 0,1 0 ∙( 0,9) 8 ≈0,43; ? ? =1−? ? ≈1−0,43=0,57

Наивероятнейшее число появлений события в независимых испытаниях Число k0 (наступление события в независимых испытаниях, в каждом из которых вероятность появления события равна p) называют наивероятнейшим если вероятность того, что событие наступит в этих испытаниях k0 раз, превышает вероятность остальных возможных исходов испытаний. Его определяют из двойного неравенства np – q ≤ k0 ≤ np + p, причем:

а) если число (np – q) – дробное, то существует одно наивероятнейшее число k0; б) если число (np – q) – целое, то существует два наивероятнейших числа, а именно k0 и k0+1; в) если число np – целое, то наивероятнейшее число k0 = np.

Пример. В урне 10 белых и 40 чёрных шаров. Вынимают подряд 14 шаров, причём цвет вынутого шара регистрируют, а затем шар возвращают в урну. Определить наивероятнейшее число появлений белого шара. Решение. Здесь n = 14, p = 10/ 50 = 1/ 5, q = 1- p = = 4/ 5. Используя двойное неравенство np - q ≤ k0 ≤ np + p при указанных значениях n, р и q, получим 14 / 5 - 4 / 5 ≤ k0 ≤ 14/ 5 + 1/ 5, т.е. 2 ≤ k0 ≤ 3. Таким образом, задача имеет два решения: k0 = 2, k0 = 3.

Пример. Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определить наивероятнейшее число попаданий в цель. Решение. Здесь n = 25, p = 0,7, q = 0,3. Следовательно, 25 · 0,7 – 0,3 ≤ k0 ≤ 25·0,7 + 0,7, т.е. 17,2 ≤ k0 ≤ 18, 2. Так как k0 – целое число, то k0 = 18.

Пример. Два равносильных шахматиста играют в шахматы. Что вероятнее – выиграть две партии из 4-х или 4 из 6 (ничьи во внимание не принимают). Решение. Т.к. играют равносильные шахматисты то вероятности выигрыша (p) и проигрыша (q) равны ½. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии – применима формула Бернулли.

Вероятность, что 2 партии из 4 будут выиграны: ? 4 2 = ? 4 2 ∙ ? 2 ∙ ? 2 = 4∙3 1∙2 ∙ 1 2 2 ∙ 1 2 2 = 6 16 Вероятность, что 3 партии из 6 будут выиграны: ? 6 3 = ? 6 3 ∙ ? 3 ∙ ? 3 = 6∙5∙4 1∙2∙3 ∙ 1 2 3 ∙ 1 2 3 = 5 16 ? ? ? >? ? ? , то вероятность выиграть 2 партии из 4-х выше чем вероятность выиграть 3 партии из 6.

Независимые испытания с несколькими исходами Пример.Игральная кость подбрасывается 15раз. Найтивероятности событий: а) выпадет ровно 10троек; б) выпадет ровно 10троек и 3единицы. Решение. а) Есть 15испытаний схемы Бернулли с вероятностью успеха1/6(успех- выпадение «3»). Вероятность 10 успехов в 15-ти испытаниях: ?(?)= ? 15 10 1 6 10 (1− 1 6 ) 15−10

б) каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение остальных граней. Пусть в одном испытании возможны m исходов:1, 2, ..., m, и исход i в одном испытании случается с вероятностью pi, где p1 +. . .+ pm = 1 Обозначим через P (n1, . . . , nm) искомую вероятность того, что в n = n1 +. . .+nm независимых испытаниях исход 1 появился n1 раз, исход 2 - n2 раз, и т.д., исход m – nm раз.

Теорема.Для любого n и любых целых n1 > 0, ..., nm>0 таких, что n1+. . .+nm= n, верна формула: ? ?1,…,?? = ?! ?1!…??! ? 1 ?1 ∙…∙ ? ? ?? Так как вероятности выпадения тройки и единицы равны по1/6, а вероятность третьего исхода (выпали любые другие грани) равна 4/6, то вероятность получить десять троек, три единицы и ещё два других очка равна: ? б = 15! 10!3!2! ∙ 1 6 10 ∙ 1 6 3 ∙ 4 6 2

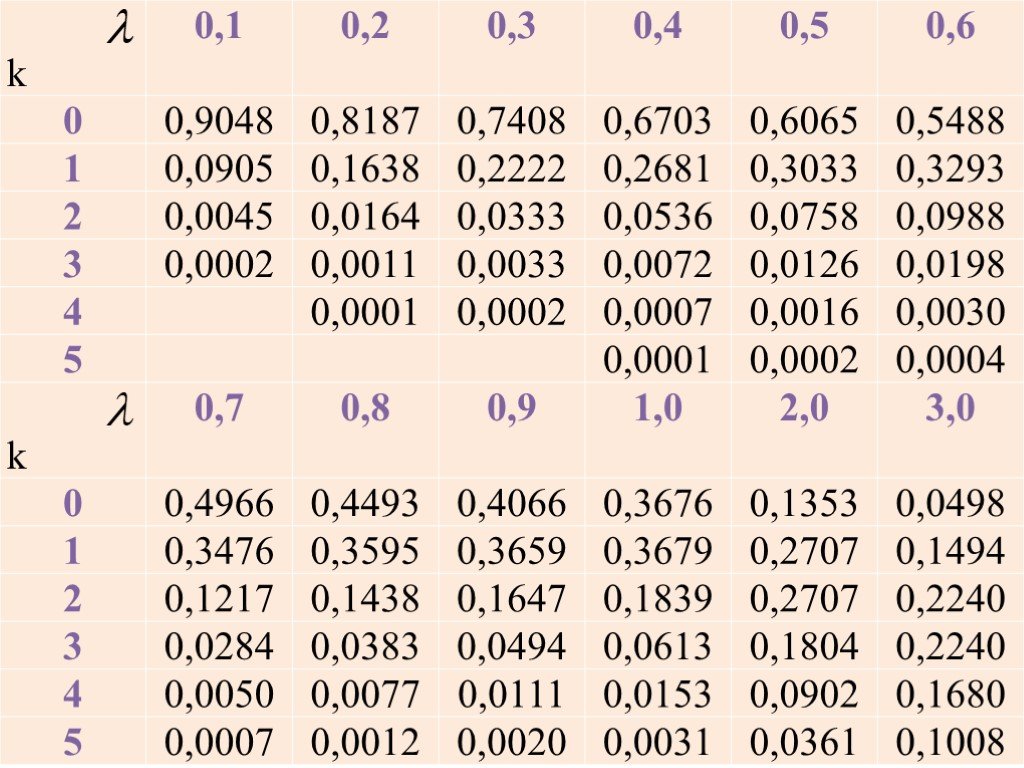
Формула Пуассона В том случае, когда вероятность появления события p мала ( p

Пример. Вероятность искажения одного символа при передаче сообщения по линии связи равна 0,001. Сообщение считают принятым, если в нём отсутствуют искажения. Найти вероятность того, что будет принято сообщение, состоящее из 20 слов по 100 символов каждое. Решение: Обозначим через А событие вероятность которого требуется найти в задаче. Переформулируем задачу в терминах схемы Бернулли n = 2000 - количество символов в сообщении;

успех: символ не искажается, р = 0,001 -вероятность успеха; m = 0 Вычислим λ = np = 2 или с помощью таблицы.

Пример. Известно, что процент брака для некоторой детали равен 0,5%. Контролер проверяет 1000 деталей. Какова вероятность обнаружить ровно 3 бракованные детали? Какова вероятность обнаружить не меньше трех бракованных деталей? Решение. Имеем 1000 испытаний Бернулли с вероятностью «успеха» р = 0,005. Применяя пуассоновское приближение с λ= np = 5:

Ответ: вероятность обнаружить ровно 3 бракованные детали равна 0,14; обнаружить не менее 3-х бракованных деталей 0,875.

Пример (задача С. Пепайса). Пепайс предложил Ньютону следующую задачу. Какое из событий более вероятно: A = {появление по крайней мере одной шестерки при подбрасывании 6 костей}, B = { появление хотя бы двух шестерок при подбрасывании 12 костей} и C = {появление не менее трех шестерок при бросании 18 костей}?

Решение. Проще найти вероятности противоположных событий, а затем их сравнивать. Для их нахождения воспользуемся теоремой Пуассона: ? ? = ? 6 0 ≈ ? 0 0! ∙ ? −? = 1 ? , где ?=??=6∙ 1 6 =1 ? ? = ? 12 0 + ? 12 1 ≈ ? 0 0! ∙ ? −? + ? 1 1! ∙ ? −? = 3 ? 2 , где ?=12∙ 1 6 =2

? ? = ? 18 0 + ? 18 1 + ? 18 1 ≈ ? 0 0! ∙ ? −? + + ? 1 1! ∙ ? −? + ? 2 2! ∙ ? −? = ? −3 +3 ? −3 + 9 2 ? −3 = 17 2? −3 , где ?=18∙ 1 6 =3 Отсюда: ? ? ? ? или 1−? ? >1−? ? >1−? ? то есть ? ? >? ? >? ?

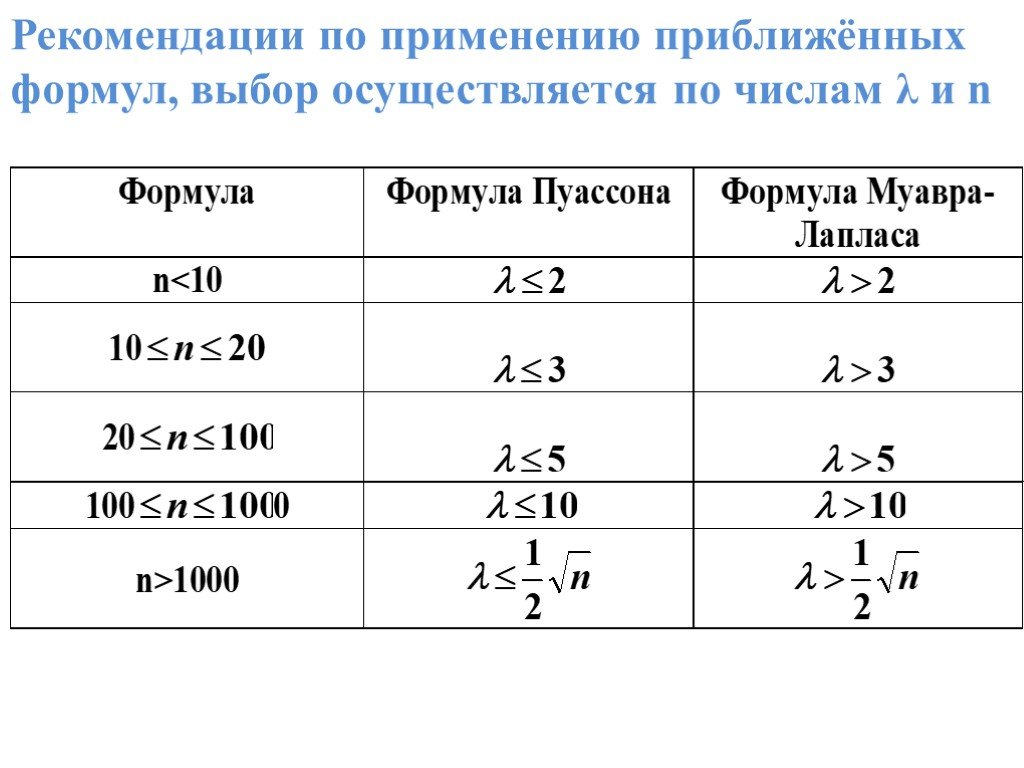
Рекомендации по применению приближённых формул, выбор осуществляется по числам λ и n