Презентация "Золотое сечение в архитектуре" (9 класс) по мхк – проект, доклад

Исследовательская работа Золотое сечение в архитектуре

Выполнила: Гусева Ольга ученица 9 «А» класса МОУ «СОШ р.п. Красный Текстильщик Саратовского района Саратовской области» Руководитель: Свириденко Ольга Владимировна 2009 год

ГОУ ДПО СарИПКиПРО Региональный конкурс «Математика в моей жизни - 2009»

Оглавление

Задачи работы Введение Гипотеза об истоке «золотого сечения» Что же такое «золотое сечение» Деление отрезка прямой по «золотому сечению» Пропорциональный циркуль Отвечает ли правилам «золотого сечения» архитектура древности Отвечает ли правилам «золотого сечения» современные здания г. Саратова Выводы

Цель:

Познакомиться с принципами золотого сечения

Задачи:

Изучить специфику «золотого сечения» в архитектуре. Выяснить, отвечает ли принципам «золотого сечения» сооружения древности. Выяснить, отвечают ли принципам «золотого сечения» здания города Саратова.

Из всех школьных предметов самое большое удовольствие я получаю от занятий математикой. Я посещаю школьный физико-математический кружок «Клуб Архимедос», люблю рисовать и просто гулять, рассматривая архитектурные здания нашего города. После окончания школы планирую поступать в СГТУ, чтобы профессионально заниматься проектированием и строительством современных красивых зданий.

Математика в моей жизни

С давних пор человек стремился окружать себя красивыми вещами. Красота и гармония стали важнейшими категориями познания, в определенной степени даже целью человека, потому что в конечном итоге художник ищет истину в красоте, а ученый - красоту в истине. Из многих пропорций, которыми издавна пользовался человек при создании гармонических произведений, существует одна, единственная и неповторимая, обладающая уникальными свойствами. Эту пропорцию называли по-разному - "золотой", "божественной", "золотым сечением", "золотым числом", "золотой серединой".

Загадка притягательной силы золотого сечения давно волнует человечество. Дополнительные данные о «золотом сечении» можно узнать из книги Г.Е. Тимердинга.

ГИПОТЕЗА ОБ ИСТОКЕ ЗОЛОТОГО СЕЧЕНИЯ

Воссоздать исторический путь открытия золотой пропорции невозможно, так как он до конца неизвестен. Например, в книге «Пробуждающаяся наука» (М., 1959) Б.Л. Вандер говорит, ссылаясь на Ямвлиха, что золотую пропорцию нашел Пифагор, но тут же добавляет: «Этому он научился у вавилонян».

Б. Л. Вандер

В III в до н. э. Евклид рассматривал пропорцию, которую мы ныне называем золотым сечением, во II книге своих «Начал», а в следующих книгах использовал эту пропорцию для построения правильного пятиугольника, десятиугольника, а также таких многогранников, как додекаэдр и икосаэдр.

«Золотое сечение» назвал эту пропорцию друг Пачоли великий итальянский живописец, скульптор, архитектор, ученый и инженер Леонардо да Винчи.

«Эта наша пропорция, высокочтимый герцог, достойна такой привилегии и такого превосходства, какие только можно высказать по поводу ее безграничных возможностей». Этими словами начиналась одна из глав книги монаха ордена францисканцев Луки Пачоли «О божественной пропорции».

«Золотым сечением» называют такое деление отрезка на две неравные части, при котором длина меньшей части так относится к длине большей части, как длина большей части к длине всего отрезка, т.е. при «золотом сечении» отрезка АВ точкой С имеет место следующая золотая пропорция:

b c a

Что же такое «Золотое сечение»

Золотая пропорция замечательна тем, что в ней кроются удивительные математические закономерности, но самое главное — считается, что формы, основанные на золотом сечении, наиболее привлекательны с эстетической точки зрения и поэтому с давних пор используются художниками, дизайнерами, архитекторами и многими другими видами профессий.

В чем же состоит замечательность «золотой пропорции»

Деление отрезка прямой по золотому сечению. BC= 1/2 AB; CD= BC

Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE= 0,618..., если АВ принять за единицу, ВЕ= 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям. Свойства золотого сечения описываются уравнением: x2 – x – 1= 0

Решение этого уравнения:

Вся история архитектуры – это история поисков гармонического единства «функции – конструкции – формы». Но все-таки одному из начал – красоте – зодчие придают особое значение. Памятник архитектуры может стать непрочным и бесполезным, но не может быть некрасивым, потому что в таком случае он из памятника превращается в строение. Французский зодчий Франсуа Блондель (1618 – 1686) в своем «Курсе архитектуры» писал о пропорциях: «Удовлетворение, которое мы испытываем, глядя на прекрасное произведение искусства, проистекает оттого, что в нем соблюдены правила и мера, ибо удовольствие в нас вызывают единственно лишь пропорции».

Архитектурные пропорции – это математика зодчего. А математика – это универсальный язык науки, поэтому мы можем сказать, что пропорции – это универсальный язык архитектуры. По сравнению с композитором или скульптором архитектор находится в более сложном положении, потому что на пути к гармонии он должен заботиться не только о «красоте», но также и о «пользе» и «прочности».

Франсуа Блондель

К сожалению, люди Древней Руси не сохранили для потомков секреты своих пропорций. Единственное дошедшее до нас античное сочинение о зодчестве – это знаменитые «Десять книг об архитектуре» римского архитектора и инженера Витрувия, время написания которых относят к 27 – 14 годам до н. э. «Десять книг» Витрувия в архитектуре, как и «Начала» Евклида в математике, - это энциклопедия античных знаний, это не только собственное сочинение автора, но и собрание известных к тому времени трудов в данной области. В своем сочинении Витрувий справедливо называет совершенными те сооружения, в которых достигнута «точная соразмерность» всех частей с основной мерой. Однако какой математический смысл вкладывал автор в эту фразу, оставался неясным.

Как именно, по какой системе древние строили свои замечательные пропорции? Это по-прежнему оставалось тайной, и здесь теоретики архитектуры могли довольствоваться лишь гипотезами. Замечательный зодчий и теоретик И. В. Жолтовский (1867 – 1959) считал, что гармония в архитектуре обретает математическое выражение в законе золотого сечения.

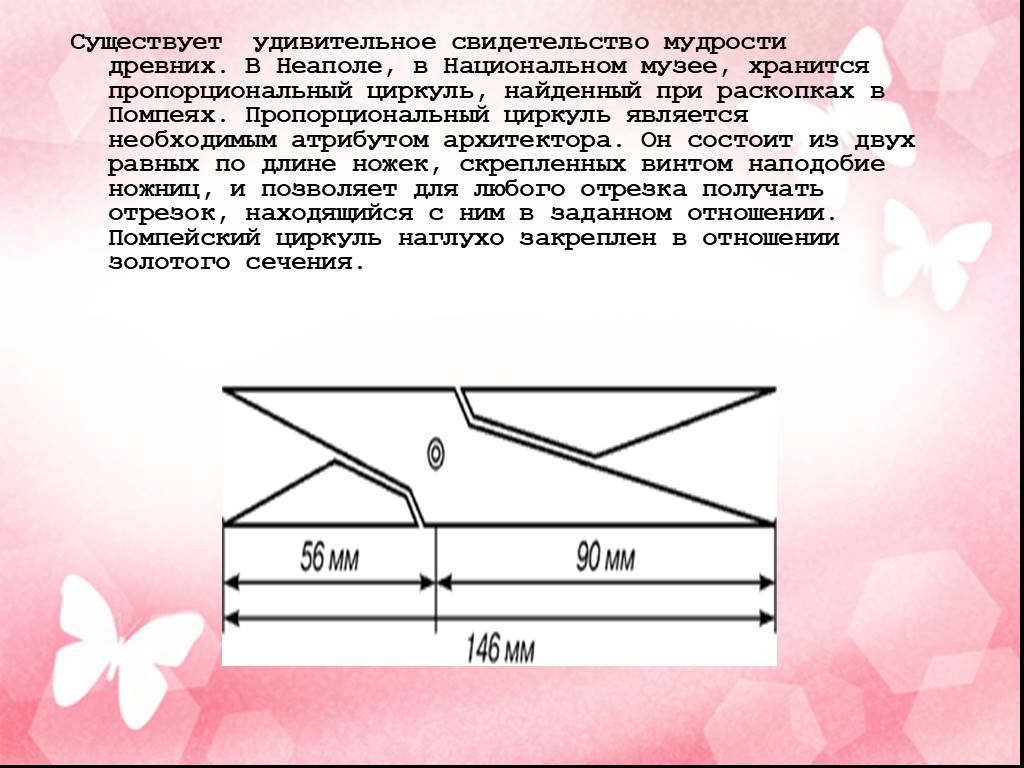
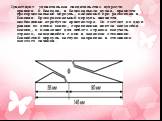
Существует удивительное свидетельство мудрости древних. В Неаполе, в Национальном музее, хранится пропорциональный циркуль, найденный при раскопках в Помпеях. Пропорциональный циркуль является необходимым атрибутом архитектора. Он состоит из двух равных по длине ножек, скрепленных винтом наподобие ножниц, и позволяет для любого отрезка получать отрезок, находящийся с ним в заданном отношении. Помпейский циркуль наглухо закреплен в отношении золотого сечения.

Циркуль найденный в Помпеях

Современный циркуль

ОДНИМ ИЗ КРАСИВЕЙШИХ ПРОИЗВЕДЕНИЙ ДРЕВНЕГРЕЧЕСКОЙ АРХИТЕКТУРЫ ЯВЛЯЕТСЯ ПАРФЕНОН (V В. ДО Н. Э.). Стремление познать тайны древних пропорций было огромным. Естественно, что каждый автор стремился проверить свою теорию на пропорциях Парфенона.

НА РИСУНКЕ ВИДЕН ЦЕЛЫЙ РЯД ЗАКОНОМЕРНОСТЕЙ, СВЯЗАННЫХ С ЗОЛОТЫМ СЕЧЕНИЕМ. ПРОПОРЦИИ ЗДАНИЯ МОЖНО ВЫРАЗИТЬ ЧЕРЕЗ РАЗЛИЧНЫЕ СТЕПЕНИ ЧИСЛА Ф=0,618...

Парфенон был и остается совершеннейшим из архитектурных сооружений. Главный вопрос о том, какой системой пропорций пользовался гениальный создатель Парфенона зодчий Иктин, пока остается открытым. Разнообразные теории, несмотря на внешнее различие, дают золотое сечение в главных вертикалях Парфенона. Так, приняв за единицу ширину торцевого фасада здания, можно получить геометрическую прогрессию, состоящую из 8 членов: расстояние между второй и седьмой колоннами равно , между третьей и шестой , между четвертой и пятой . Аналогичные закономерности мы видим и в построении здания по высоте. Объединив их, получаем прогрессию: . Указанным членам ряда отвечают основные пропорции фасада Парфенона . Высота крыши Парфенона относится к расстоянию между крышей и капителями колонн, как . . .

Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр - дам де Пари)

Многие пытались разгадать секреты пирамиды фараона Хеопса в Гизе. Пирамида Хеопса, одна из трёх пирамид в Гизе и находится неподалёку от Каира. В отличие от других египетских пирамид это не гробница, а скорее неразрешимая головоломка из числовых комбинаций. Замечательные изобретательность, мастерство, время и труд архитекторов пирамиды, использованные ими при возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была до письменной, до иероглифической и символы были единственным средством записи открытий. Ключ к геометро - математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты : 1. В основании лежит квадрат со сторонами по 230.35 метров (b=230.35 м); 2. Высота пирамиды Хеопса: 146.71 метра (h=146.71 м); 3. Боковая грань пирамиды представляет собой равнобедренный прямоугольный треугольник - угол при вершине 90º, два угла внизу - по 45º; 4. Всего треугольных граней 4 (естественно, т.к. в основании - квадрат).

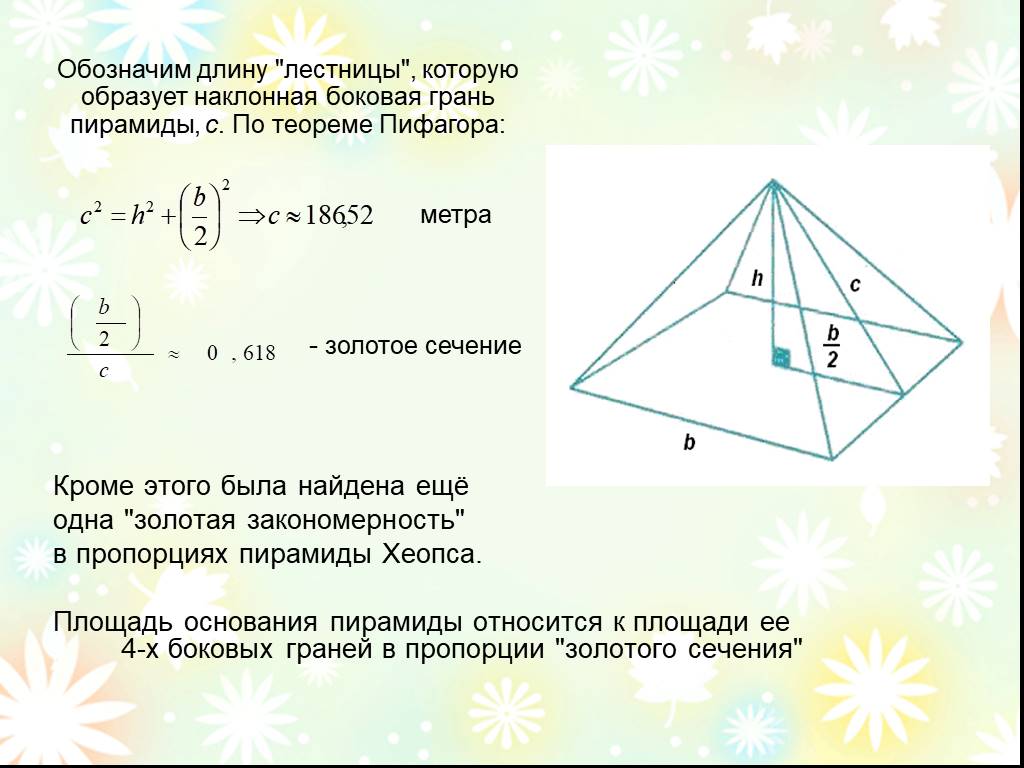
Кроме этого была найдена ещё одна "золотая закономерность" в пропорциях пирамиды Хеопса. Площадь основания пирамиды относится к площади ее 4-х боковых граней в пропорции "золотого сечения"

Обозначим длинy "лестницы", которую образует наклонная боковая грань пирамиды, с. По теореме Пифагора:

метра - золотое сечение

Храм был возведен по указу императора Александра III в 1883–1907 годах по совместному проекту архитектора Альфреда Парланда и архимандрита Игнатия в Санкт - Петербурге, на месте, где 1 марта 1881 года был смертельно ранен император Александр II. Архитектурное здание полностью соответствует правилам «золотого сечения»

Собор Воскресения Христова

Храм Василия Блаженного — православный храм, расположенный на Красной площади в Москве. Широко известный памятник русской архитектуры. До XVII века обычно назывался Троицким, так как первоначальный деревянный храм был посвящён Святой Троице. Храм Василия Блаженного полностью соответствует правилам «золотого сечения».

Рассуждения о золотом сечении в архитектуре хочется закончить примером пропорционального строя храма Василия Блаженного в Москве (рис. 19). За «целое» принята высота храма. Пропорции храма определяются восемью членами ряда золотого сечения: Многие из членов ряда неоднократно повторяются в пропорциях этого затейливого архитектурного сооружения, но всегда благодаря аддитивному свойству золотого сечения мы уверены в том, что части сойдутся в целое, т.е. , , , и т.д. Таким образом, аддитивное свойство золотого сечения делает эту геометрическую пропорцию единственной и неповторимой.

Отвечают ли пропорциям золотого сечения архитектурные сооружения г. Саратова?

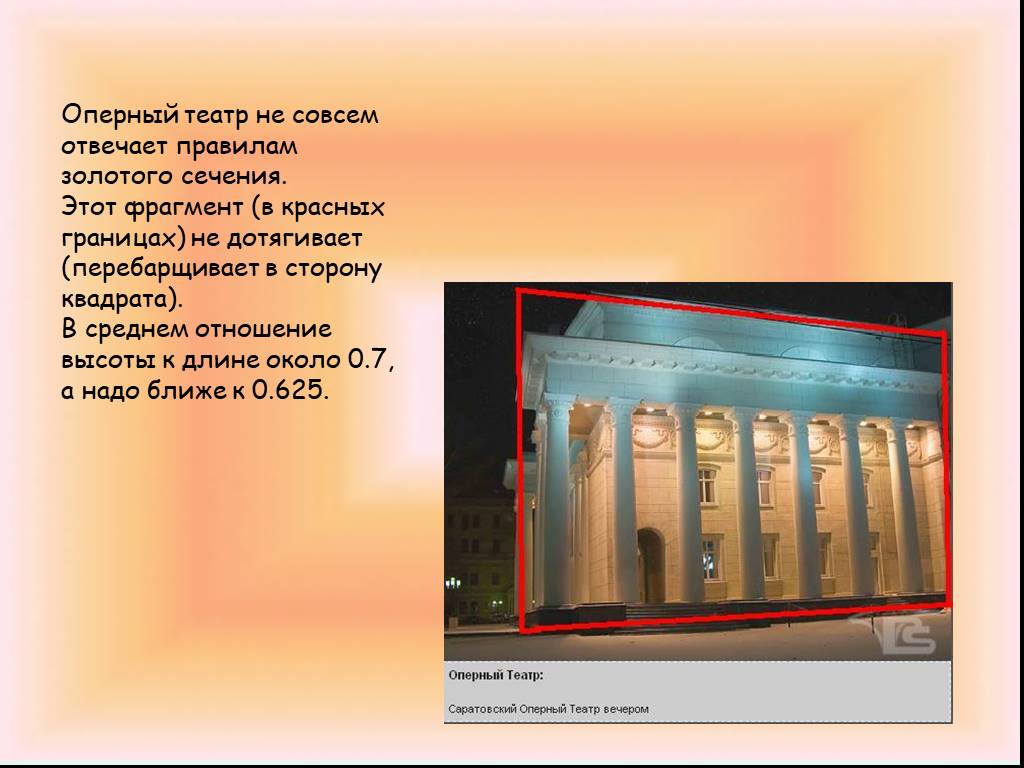
Оперный театр не совсем отвечает правилам золотого сечения. Этот фрагмент (в красных границах) не дотягивает (перебарщивает в сторону квадрата). В среднем отношение высоты к длине около 0.7, а надо ближе к 0.625.

Здание администрации города Саратова не отвечает правилам золотого сечения. Если посчитать отношение высоты к длине, то получается 0.875, а надо ближе к 0.625.

Музей Радищева полностью соответствует правилам «золотого сечения»

Отношение длины к высоте равно примерно 0.4, а надо ближе к 0.625. Следовательно, цирк не отвечает правилам «золотого сечения»

Отношение высоты к длине приблизительно 0.7, а надо ближе к 0.625.

Саратовский Государственный Университет

Гостиница «Волга» отвечает правилам «золотого сечения»

Два высших начала культуры. Их высшая цель – быть дополняющими друг друга. Из многих искусств, допускающих математическое описание, я слегка коснулась только архитектуры. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства. Поэтому, именно в математике, лежащей в основе гармонии искусства, посвящена эта работа.

Наука и искусство –

Вывод:

В ходе работы я познакомилась с правилами «золотого сечения» . Самые известные сооружения в мире несмотря на их возраст, отвечают принципам «золотого сечения», что к сожалению, нельзя сказать, про зданиям современности. Когда я стану архитектором я постараюсь проектировать и строить здания которые отвечают правилам «золотого сечения».

Библиография

Ресурсы Интернета: http://goldsech.narod.ru/ http://www.photoline.ru/tcomp1.htm http://rustimes.com/blog/page_all_102.html http://www.harunyahya.ru/article_zolotoe_sechenir.php http://www.zaitseva-irina.ru/html/f1103454898.html http://www.milogiya2007.ru/uzakon2_2.htm http://www.log-in.ru/articles/432/