Презентация "Интерференция. Дифракция" по физике – проект, доклад
Презентацию на тему "Интерференция. Дифракция" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Дисперсия. Интерференция. Дифракция
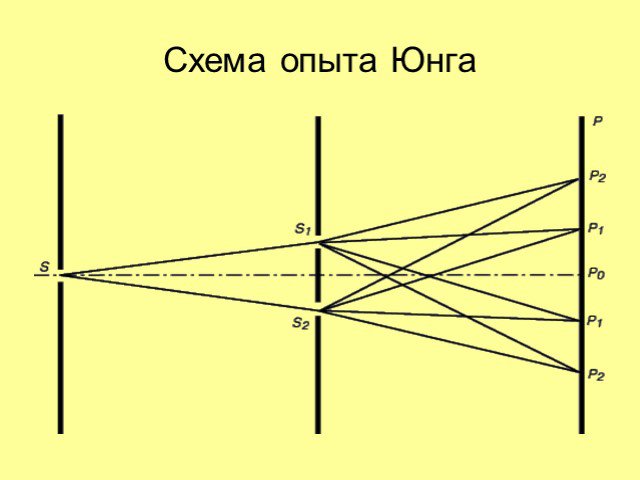
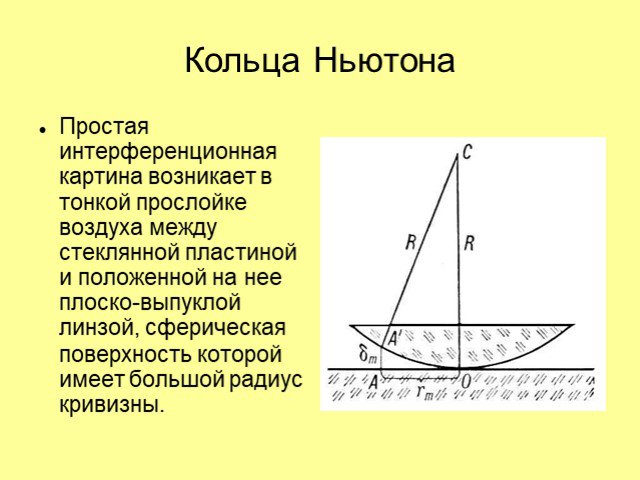
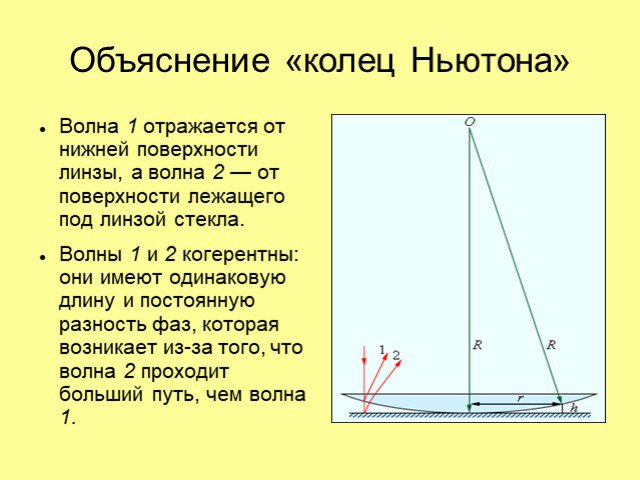
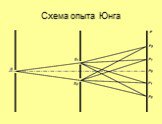
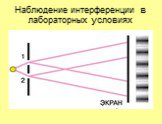
Дисперсия. Условие максимума. Условие минимума. . Наблюдение колец Ньютона. Кольца Ньютона в зеленом и красном цвете. Схема опыта Юнга. . . Дифракционная ...Дифракция и интерференция света
Сложение волн волн на поверхности жидкости. Концентрические круговые волны с источниками в различных точках на поверхности воды, возникшие в результате ...Интерференция волн
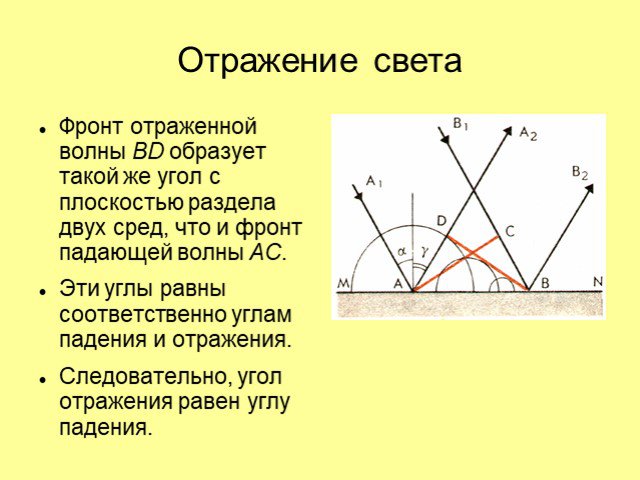
Интерференция -. явление наложения волн, при котором наблюдается устойчивое о времени усиление или ослабление результирующих колебаний в различных ...Оптика. Интерференция света и её применение
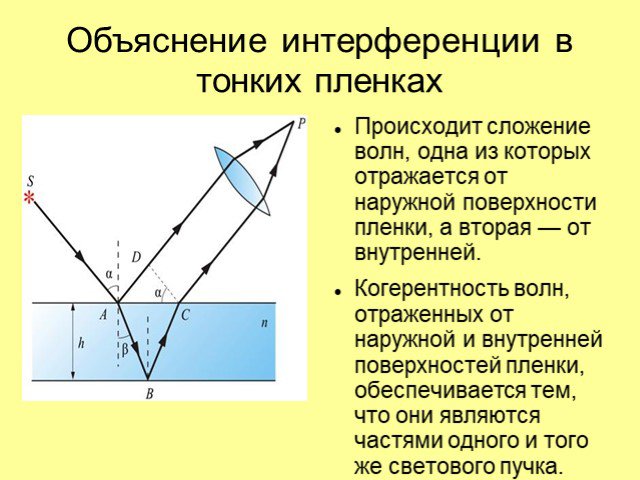
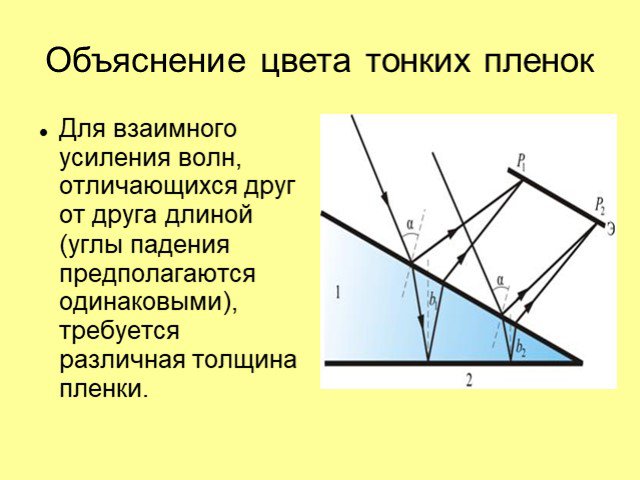
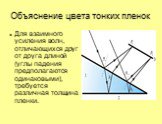
Интерференция света. Часть 2 Лекция 10. Условие пространственной когерентности Интерференция в тонких пленках Применение явлений интерференции. Условие ...Интерференция света в тонких пленках
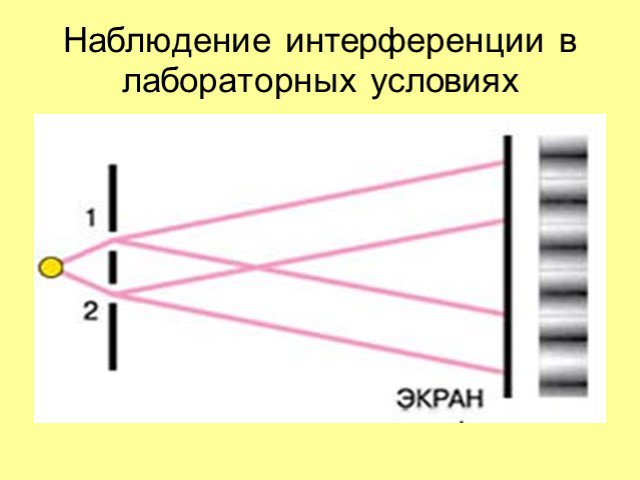
Цель работы: пронаблюдать явление интерференции света с использованием тонких пленок. Задачи: рассмотреть теорию интерференции волн и ее частного ...Интерференция света
Цели урока: Познакомиться с явлениями, в которых проявляются волновые свойства света. Узнать при каких условиях они проявляются. Научиться распознавать ...Интерференция света
Интерференция света – нелинейное сложение интенсивностей двух или нескольких световых волн. Это явление сопровождается чередующимися в пространстве ...Интерференция механических волн
Сложение волн. Очень часто в среде одновременно распространяется несколько различных волн. Проще всего проследить за наложением механических волн, ...Дифракция света
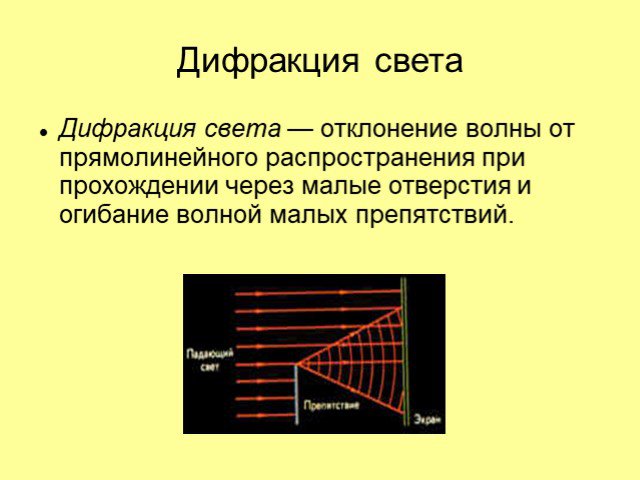
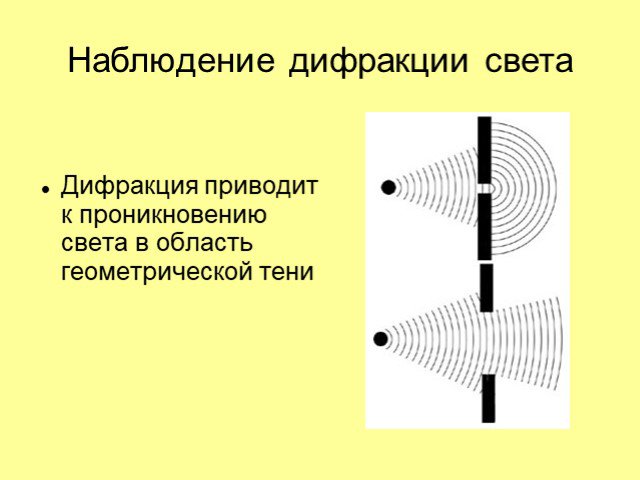
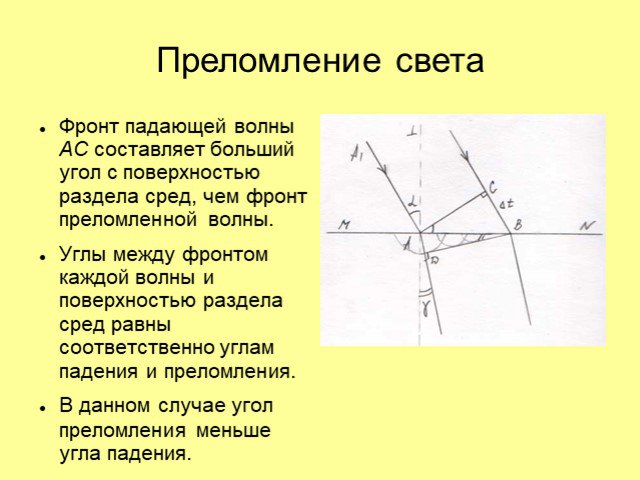
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает ...Дифракция механических и световых волн
Повторение явления интерференции и его применения. 1.Понятие явления. 2.При каком условии волны интерферируют. 3.Понятие когерентных волн. 4.Каким ...Дифракция волн
Поведение звуковых и механических волн. Поведение волны определяется соотношением между длиной волны λ и размером препятствия d. Дифракция, 1663 г. ...Дифракция
Дифракция механических волн. Дифракция – отклонение от прямолинейного распространения и огибание волнами препятствий. Общее свойство волн любой природы. ...Дифракция
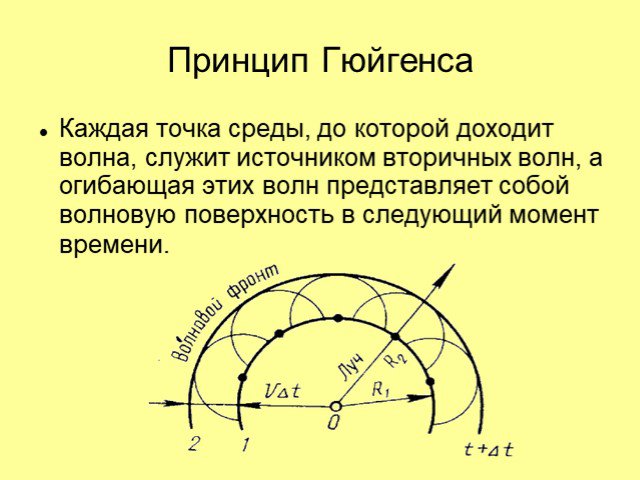
Построение Гюйгенса для плоской и сферической волн. Пусть волна падает на отверстие в непрозрачном экране (рис.). Согласно Гюйгенсу, каждая точка ...Интерференция волн
Принцип суперпозиции. Точка, в которой «встретились» две волны, участвует в двух колебаниях. Результирующее смещение точки от положения равновесия ...Дифракция света
Характерным проявлением волновых свойств света является дифракция света —. отклонение от прямолинейного распространения на резких неоднородностях ...Интерференция двух волн
Интерференция -. Сложение в пространстве двух или более волн, в результате которого возникает устойчивая картина распределения амплитуд результирующих ...Дифракция света принцип Гюйгенса
В 1665г.итальянским ученым Гримальди были открыты такие явления, как интерференция и дифракция света. В темную комнату сквозь маленькое отверстие ...Интерференция света
Бавкун Т.Н. МБОУ ОСОШ№3 г.Очер. ИНТЕРФЕРЕНЦИЯ СВЕТА -. сложение двух (или нескольких) световых волн, при котором в одних точках пространства происходит ...Дифракция света. Дифракционная решетка
Повторим пройденный материал. Дисперсия это… Цветность световых волн зависит от… Источники называются когерентными, если… Скорость какого излучения ...Интерференция света
§§ Оптический путь. x – геометрический путь. Lopt = nx – оптический путь. Произведение показателя преломления на длину пути называется оптической ...Конспекты
Интерференция света. Дифракция света. Линзы. Дефекты зрения. Очки
Урок № 57-169. Интерференция света. Дифракция света. Линзы. Дефекты зрения. Очки. . . Интерференция света -. сложение в пространстве двух и более ...Электромагнитная природа света. Интерференция света
Разработка урока физики в 9 классе по теме "Электромагнитная природа света. Интерференция света". (класс с углублённым изучением физики). Долгова ...Интерференция механических волн
Разработка плана-конспекта урока физики. ФИО педагога Беленкова Анастасия Сергеевна. Автор УМК Мякишев Г.Я. 11 класс. Тема урока Интерференция ...Дифракция света
«Дифракция света». Курносова Светлана Александровна. Учитель физики МБОУ «Кировская средняя общеобразовательная школа», п. Кировский. Смоленского ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 апреля 2015
Категория:Физика
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию