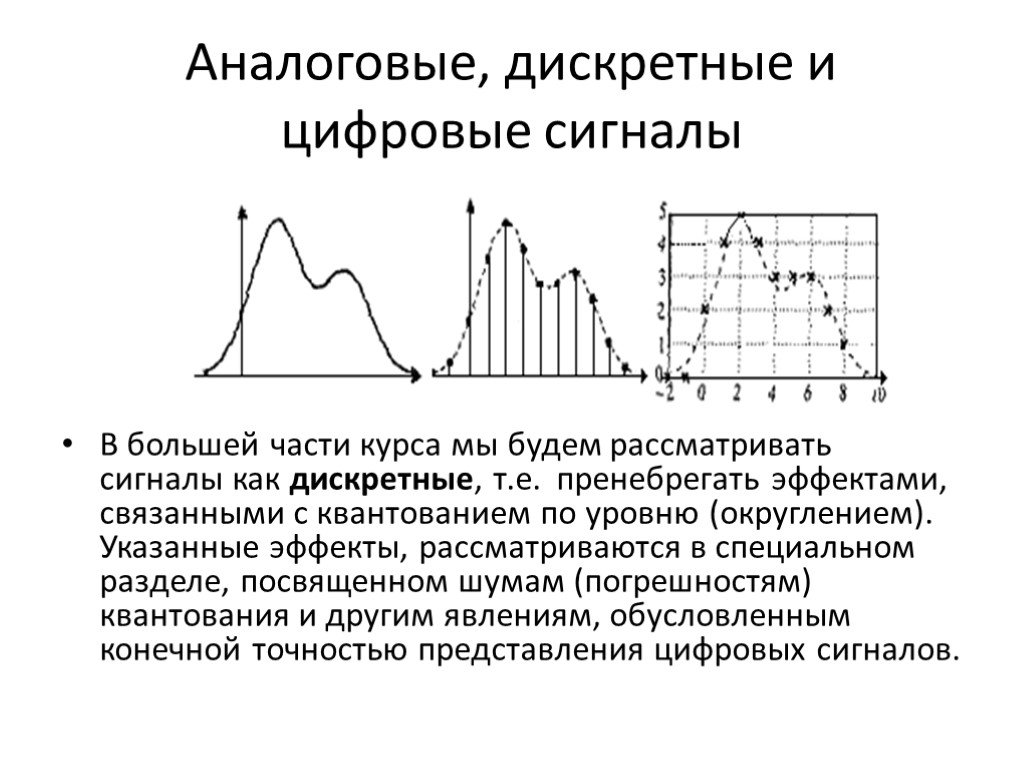
Презентация "Тестовые функции сигнала" по физике – проект, доклад
Презентацию на тему "Тестовые функции сигнала" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
Виды излучений физика
Открытие радиоактивности. РАДИОАКТИВНОСТЬ – превращение атомных ядер в другие ядра, сопровождающееся испусканием различных частиц и электромагнитного ...Самостоятельные способы усиления Wi-Fi сигнала
С развитием Интернет-технологий в мире несомненную популярность приобрели системы беспроводной связи Wi-Fi. Ныне, в общественных местах и дома человек ...Свободное падение физика
Свободное падение тел впервые исследовал Галилей, который установил, что свободно падающие тела движутся равноускоренно с одинаковым для всех тел ...Силы и виды сил
Виды сил. Сила упругости. Сила упругости- это сила, возникающая при деформации тела. Сила упругости направлена против деформации. Деформация- это ...Прикладная физика
Лекция 1 Материалы курса, задания Цели, задачи ПФ Разделы курса. В осеннем семестре 22 лекции. Предстоит защитить и сдать 2 реферата, написать 1 контрольную ...Раздел молекулярная физика
Молекулярная физика – раздел физики, в котором изучаются физические свойства тел в различных агрегатных состояниях на основе рассмотрения их молекулярного ...Молекулярная физика и термодинамика
Тепловое равновесие. Температура. Молекулярная физика и термодинамика изучают свойства и поведение макроскопических систем, т.е. систем, состоящих ...Невесомость физика
ЦЕЛЬ: Дать понятие невесомости в комплексном виде. ЗАДАЧИ: Разобраться в механизме возникновения этого явления; Описать этот механизм математически ...Атомная физика
Факты, свидетельствующие о сложном строении атома. Периодическая система Д.И. Менделеева Электролиз Открытие электрона Катодные лучи Радиоактивность. ...Молекулярная физика
Основные положения МКТ. Все вещества состоят из молекул, которые разделены промежутками. Молекулы беспорядочно движутся. Между молекулами есть силы ...«Электромагнит» физика
2. Как располагаются железные опилки в магнитном поле прямого тока? 3. Что называют магнитной линией магнитного поля? 4. Для чего вводят понятие магнитной ...Альтернативные виды топлива
Наше настоящее. Цель исследований. Изучение современных заменителей топлива и возможности их применения в качестве альтернативы бензину и дизелю. ...«Сообщающиеся сосуды» физика
Цель: изучить особенности сообщающихся сосудов и сформулировать основной закон сообщающихся сосудов. Опыт с двумя трубками. Опыт с сосудами разной ...«Световые волны» физика
Оглавление:. Принцип Гюйгенса Закон отражения света Закон преломления света Полное отражение Линза Расчёт увеличения линзы Дисперсия света Интерференция ...«Оптические приборы» физика
Содержание. 1.Телескоп 2.Строение телескопа 3.Разновидности телескопов 4.Рефлекторы 5.Использование телескопов 6.Микроскоп 7.Создание микроскопа 8.Использование ...Тепловые двигатели физика
СОДЕРЖАНИЕ. Содержание Тепловой двигатель Тепловые машины и развитие техники Кто создал тепловые двигатели Виды тепловых двигателей Принцип работы ...Атомная физика
План урока 1. Из истории физики 2. Модель Томсона 3. Опыт Резерфорда 4. Противоречия 5.Постулаты Бора 6.Энергетическая диаграмма атома водорода 7. ...«МКТ» физика
Содержание. Молекулярная физика Основы молекулярно-кинетической теории строения вещества (МКТ) Температура и внутренняя энергия тела Характеристика ...Атомная физика
Атомная физика. Атомная физика на стыке XIX и ХХ вв. в науке свершились открытия, заставившие заколебаться сложившуюся картину мира. Представлениям, ...Молекулярная физика и термодинамика
Молекулярно-кинетическая теория. Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:10 июня 2019
Категория:Физика
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию