Слайд 1ТЕПЛОМАССОПЕРЕНОС В ЯДЕРНО-ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ
Слайд 2Тема № 6 КОНВЕКТИВНЫЙ ТЕПЛОМАССООБМЕН В ОДНОФАЗНЫХ ПОТОКАХ
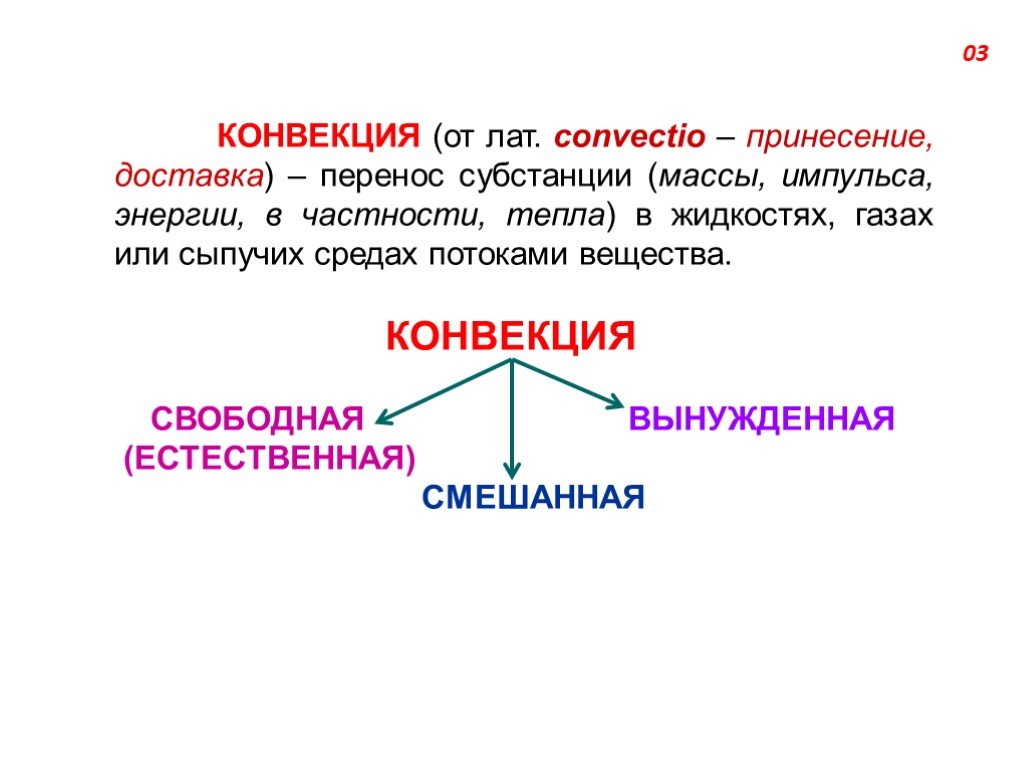
Слайд 3КОНВЕКЦИЯ (от лат. convectio – принесение, доставка) – перенос субстанции (массы, импульса, энергии, в частности, тепла) в жидкостях, газах или сыпучих средах потоками вещества. КОНВЕКЦИЯ СВОБОДНАЯ ВЫНУЖДЕННАЯ (ЕСТЕСТВЕННАЯ) СМЕШАННАЯ
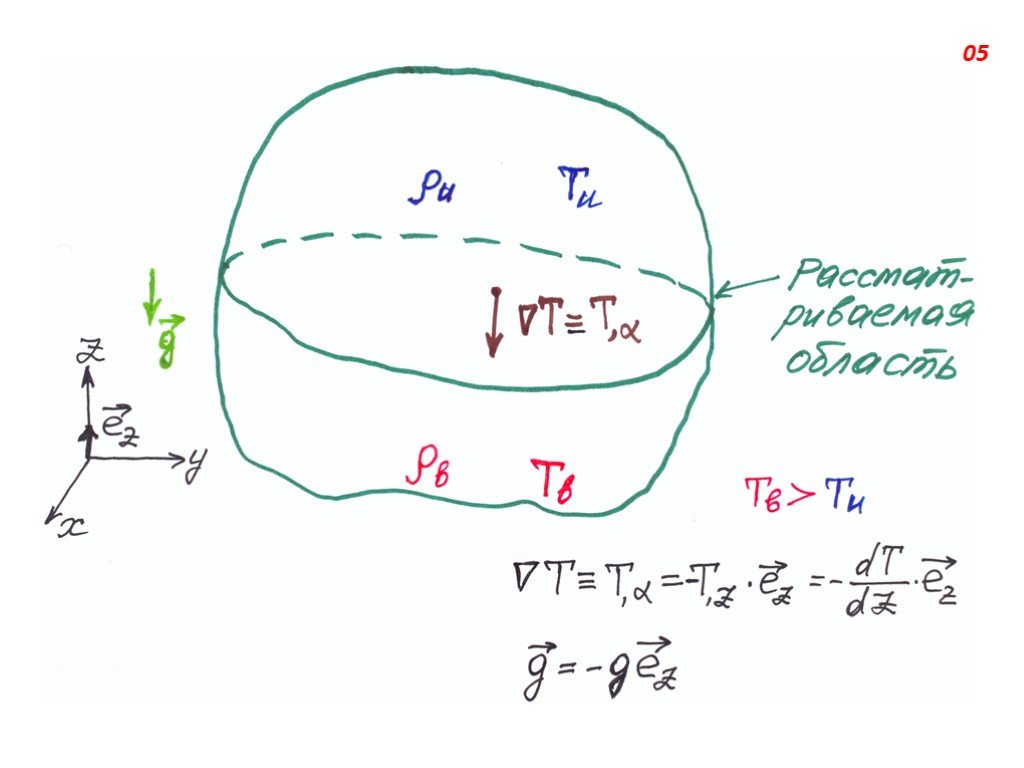
Слайд 4СВОБОДНАЯ (ЕСТЕСТВЕННАЯ) КОНВЕКЦИЯ возникает под действием неоднородного поля массовых сил (например, гравитационных; в системе, движущейся с ускорением), неоднородность которого обусловлена неоднородной (вследствие теплообмена) плотностью текущей среды. Вещество, нагретое сильнее, имеет меньшую плотность и под действием архимедовой силы перемещается относи- тельно менее нагретого вещества. Направление силы , а следовательно, и конвекция для нагретых объёмов вещества противоположно направлению силы тяжести. Конвекция приводит к выравниванию температуры вещества.
Слайд 5
Слайд 6При стационарном подводе теплоты к веществу в нём возникают стационарные конвекционные потоки, переносящие теплоту от более нагретых слоев к менее нагретым. С уменьшением разности температур между слоями интенсивность конвекции уменьшается. При высоких значениях теплопроводности и вязкости среды конвекция также оказывается ослабленной. На конвекцию ионизованного газа (например, солнечной плазмы) существенно влияет магнитное поле и состояние газа (степень его ионизации и т.д.). В условиях невесомости естественная конвекция невозможна.
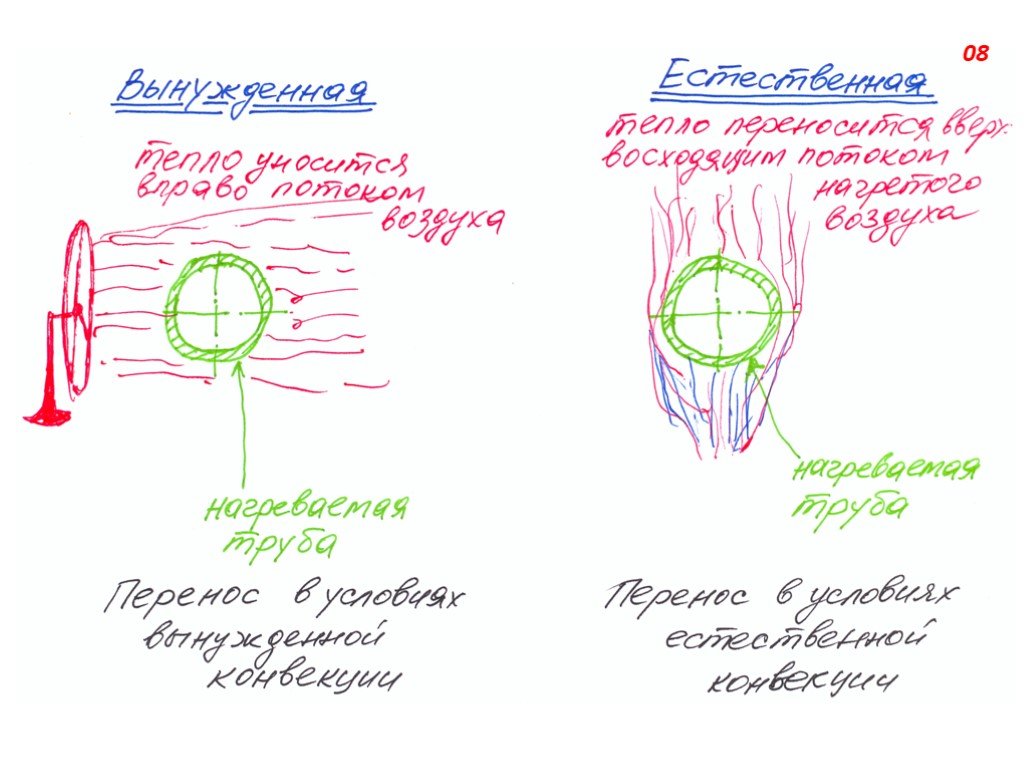
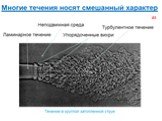
Слайд 7ВЫНУЖДЕННАЯ КОНВЕКЦИЯ – перемещение теплоносителя относительно поверхности теплообмена вызвано какими-либо внешними побудителями (насос, мешалки и т.п.). Интенсивность переноса теплоты здесь зависит не только от перечисленных выше факторов, но и от скорости вынужденного движения вещества.
Слайд 8
Слайд 9
Слайд 10Конвекция широко распространена в природе: в нижнем слое земной атмосферы, морях и океанах, в недрах Земли, на Солнце (в слое до глубины ~20÷30% радиуса Солнца от его поверхности) и т.д. С помощью конвекции осуществляют охлаждение или нагревание жидкостей и газов в различных технических устройствах (Конвективный теплообмен).
Слайд 11КОНВЕКТИВНЫЙ ТЕПЛООБМЕН – процесс переноса тепла, происходящий в движущихся текучих средах (жидкостях либо газах) и обусловленный совместным действием двух механизмов переноса тепла – собственно конвективного переноса и теплопроводности. Таким образом, в случае конвективного теплообмена распространение тепла в пространстве осуществляется за счёт переноса тепла при перемещении текучей среды из области с более высокой температурой в область с меньшей температурой, а также за счёт теплового движения микрочастиц и обмена кинетической энергией между ними.

Слайд 12В связи с тем, что для неэлектропроводных сред интенсивность конвективного переноса очень велика по сравнению с теплопроводностью, последняя (теплопроводность) при ламинарном течении играет заметную роль лишь в переносе тепла в направлении, поперечном течению потока. Роль теплопроводности при конвективном теплообмене более значительна при движении электропроводных сред (например, жидких металлов). В этом случае теплопроводность существенно влияет и на перенос тепла в направлении движения жидкости. При турбулентном течении основную роль в процессе переноса тепла поперек потока играет пульсационное перемещение турбулентных вихрей поперек течения жидкости.
Слайд 13Участие теплопроводности в процессах конвективного теплообмена приводит к тому, что на эти процессы оказывают существенное влияние теплофизические свойства среды: коэффициент теплопроводности, теплоёмкость, плотность.
Слайд 14В связи с тем, что в процессах конвективного теплообмена главную роль играет конвективный перенос, эти процессы в значительной мере зависят от характера движения жидкости, то есть от значения и направления скорости течения теплоносителя, от распределения скоростей в потоке, от режима движения жидкости (ламинарное течение либо турбулентное). При больших (сверхзвуковых) скоростях движения газа на процессы конвективного теплообмена начинает влиять распределение давления в потоке. На практике встречаются случаи, когда приходится учитывать как вынужденную, так и свободную конвекцию. В этом случае употребляется термин смешанная конвекция.

Слайд 15Наиболее интересным с точки зрения технических приложений случаем конвективного теплообмена является конвективная теплоотдача. КОНВЕКТИВНАЯ ТЕПЛООТДАЧА – перенос тепла между некоторой выделенной поверхностью и движущейся относительно её (поверхности) текущей средой (жидкостью, газом). В качестве выделенной поверхности теплообмена обычно рассматривается поверхность твёрдого тела, но это может быть и граница раздела фаз или различных жидкостей.
Слайд 16Задача расчёта состоит в нахождении плотности теплового потока на границе раздела фаз, то есть величины, показывающей, какое количество тепла получает или отдает единица поверхности раздела фаз за единицу времени. Помимо указанных выше факторов, влияющих на процесс конвективного теплообмена, плотность теплового потока зависит также от формы и размеров тела, от степени шероховатости поверхности, а также от температур поверхности и теплоотдающей или тепловоспринимающей среды.
Слайд 17Различают два типа задач конвективного теплообмена.
ТЕПЛООБМЕН ПРИ ТЕЧЕНИИ В КАНАЛАХ (ВНУТРЕННИЕ ЗАДАЧИ) теплообмен между стенками канала и потоком теплоносителя в нём.
ТЕПЛООБМЕН ПРИ ВНЕШНЕМ ОБТЕКАНИИ ТЕЛ теплообмен между поверх-ностью и омывающим её снаружи потоком тепло-носителя
Для характеристики интенсивности конвективного теплообмена используются местный и средний коэффициенты теплоотдачи.
Слайд 18Местный коэффициент теплоотдачи
‒ локальная плотность теплового потока на поверхности теплообмена
‒ расчётный температурный напор
Слайд 19В задачах теплообмена при внешнем обтекании тел
‒ начальный температурный напор
‒ температура стенки
‒ начальная температура ‒ температура набегающего потока теплоносителя вдали от поверхности теплообмена
Слайд 20В задачах теплообмена при течении в каналах
‒ местный температурный напор
‒ средняя калориметрическая (среднемассовая) температура теплоносителя в рассматриваемом сечении канала
Слайд 21
Слайд 22
Слайд 23
Слайд 24
Слайд 25
Слайд 26
Слайд 27
Слайд 28
Слайд 29
Слайд 30В общем случае коэффициент теплоотдачи является функцией ● формы обтекаемого тела, ● размеров обтекаемого тела, ○ режима течения, ■ скорости теплоносителя, ■ температуры теплоносителя, ■ физических свойств теплоносителя, □ направления теплового потока.
Слайд 31Основной и наиболее трудной проблемой в расчётах процессов конвективной теплоотдачи является нахождение коэффициента теплоотдачи. Коэффициент теплоотдачи возрастает при увеличении скорости движения среды и при переходе от ламинарного режима движения к турбулентному в связи с интенсификацией конвективного переноса. Он также всегда больше для тех сред, у которых выше коэффициент теплопроводности. Коэффициент теплоотдачи существенно повышается, если на поверхности происходит фазовый переход (например, испарение или конденсация), всегда сопровождающийся выделением (поглощением) скрытой теплоты. На значение коэффициент теплоотдачи сильное влияние оказывает массообмен на поверхности.

Слайд 32Современные методы описания процесса конвективного теплообмена, основанные на теории пограничного слоя, позволяют получить теоретические (точные или приближённые) решения для некоторых достаточно простых ситуаций. В большинстве же встречающихся на практике случаев коэффициент теплоотдачи определяют экспериментальным путём. При этом как результаты теоретических решений, так и экспериментальные данные обрабатываются методами теории подобия и представляются обычно в следующем безразмерном виде: – для вынужденной конвекции, – для свободной конвекции. где – критериальные числа Нуссельта, Рейнольдса, Прандтля и Грасгоффа, соответственно.
Слайд 33Критериальное число РЕЙНОЛЬДСА – критерий режима движения. Характеризует динамический режим потока, являясь мерой отношения действующих в потоке сил инерции и сил вязкого трения (молекулярного трения) где – скорость потока, ; – плотность жидкости, ; – характерный размер, ; – динамическая вязкость, ; – кинематическая вязкость, .
Слайд 34
Слайд 35Рейнольдс, Рейнолдс (Reynolds) Осборн (23.8.1842, Белфаст, — 21.2.1912, Уотчет, Сомерсетшир), английский физик и инженер, член Лондонского королевского общества (с 1877). Окончил Кембриджский университет (1867). Профессор Манчестерского университета (1868). С 1888 возглавил Витвортовскую инженерную лабораторию. Основные труды по теории динамического подобия течений вязкой жидкости, по теории турбулентности и теории смазки. В 1876—83 экспериментально установил критерий перехода ламинарного течения в цилиндрических трубах в турбулентное. Предложил дифференциальные уравнения для осреднённого движения жидкости, учитывающие дополнительные напряжения (турбулентные напряжения). Внёс большой вклад в развитие гидродинамической теории смазки. Исследовал также явление кавитации на лопасти вращающегося винта, атмосферную рефракцию звука, групповую скорость распространения волн на свободной поверхности воды, теплопередачу от твёрдых стенок к жидкости и т. д.

Слайд 36Критериальное число Грасгофа является мерой отношения сил инертно-гравитационной конвекции и сил вязкого трения. g ‒ ускорение свободного падения, м/с2; β ‒ коэффициент объёмного расширения, К‒1; ΔT ‒ разность температур, К; ν ‒ кинематический коэффициент вязкости, м2/с; L ‒ характерный размер, м.
Слайд 37Критериальное число Прандтля является мерой подобия температурных и скоростных полей в потоке теплоносителя. При Pr=1 и P,α=0 поля температур и скоростей подобны. ν ‒ кинематический коэффициент вязкости, м2/с. а ‒ коэффициент температуропроводности, м2/с.
Слайд 38Число Прандтля — физическая характеристика среды и зависит только от её термодинамического состояния. У газов число Прандтля с изменением температуры практически не изменяется: для двухатомных газов для трёх- и многоатомных У неметаллических жидкостей число Прандт-ля изменяется с изменением температуры тем значитель-нее, чем больше вязкость жидкости. Для воды при 0 °С , а при 100 °С . Для трансформаторного масла при 0 °С , а при 100 °С
Слайд 39У жидких металлов Pr

Слайд 40Прандтль (Prandtl) Людвиг (4.2.1875, Фрейзинг, Бавария, — 15.8.1953, Гёттинген), немецкий учёный в области механики, один из основателей экспериментальной аэродинамики. Окончил Высшее политехническое училище в Мюнхене. Профессор Высшего технического училища в Ганновере (с 1901), Гёттингенского университета (с 1904), директор института гидроаэродинамики кайзера Вильгельма в Гёттингене (1925—47). Основные труды по теории упругости и пластичности, гидроаэромеханике, газовой динамике и динамической метеорологии. В 1904 ввёл представление о пограничном слое и объяснил сопротивление формы при обтекании тела отрывом пограничного слоя. Создал теорию самолётного крыла конечного размаха, разработал методы упрощённого решения соответствующих уравнений, исследовал крыло с наивыгоднейшим распределением циркуляций, рассмотрел случай нестационарного решения (совместно с Бирнбаумом), ввёл чёткое понятие индуцированного сопротивления, дал формулу для его определения и т.д. Изучал турбулентное течение в трубах, турбулентность свободной атмосферы, переход от ламинарного течения к турбулентному, исследовал сверхзвуковое истечение газов и паров под давлением и разработал линеаризованную теорию крыла в дозвуковом потоке сжимаемого газа. Именем Прандля названы уравнения, понятия, приборы. Основал школу в прикладной гидроаэромеханике.

Слайд 41Критериальное число Нуссельта – «безразмерный коэффициент теплоотдачи». Является мерой отношения характерного размера L и толщины теплового пограничного слоя δТ. характеризует связь между интенсивностью теплоотдачи и температурным полем в пограничном слое. α ‒ коэффициент теплоотдачи, Вт/(м2·К); fluid – коэффициент теплопроводности жидкости, Вт/(м·К); L ‒ характерный размер, м.
Слайд 42На границе с обтекаемым телом скорость жидкости равна нулю. Следовательно, тепловой поток в пристенном слое обусловлен только теплопроводностью
Слайд 43Критериальное число Пекле – Критерий теплового подобия. Является мерой отношения конвективного и кондуктивного (обусловленного теплопроводностью, то есть молекулярного) теплопереноса. Характеризует связь между интенсивностью теплоотдачи и температурным полем в пограничном слое. w ‒ скорость теплоносителя, м/с; а – коэффициент температуропроводности жидкости, м2/с; L ‒ характерный размер, м.
Слайд 44Критериальное число Стантона – Является мерой отношения конвективного теплообмена «стенка–поток» и конвективного уноса тепла потоком теплоносителя. α ‒ коэффициент теплоотдачи, Вт/(м2·К); w ‒ скорость теплоносителя, м/с; ρ ‒ плотность теплоносителя, кг/м3; ср ‒ удельная теплоёмкость теплоносителя, Дж/(кг·к).
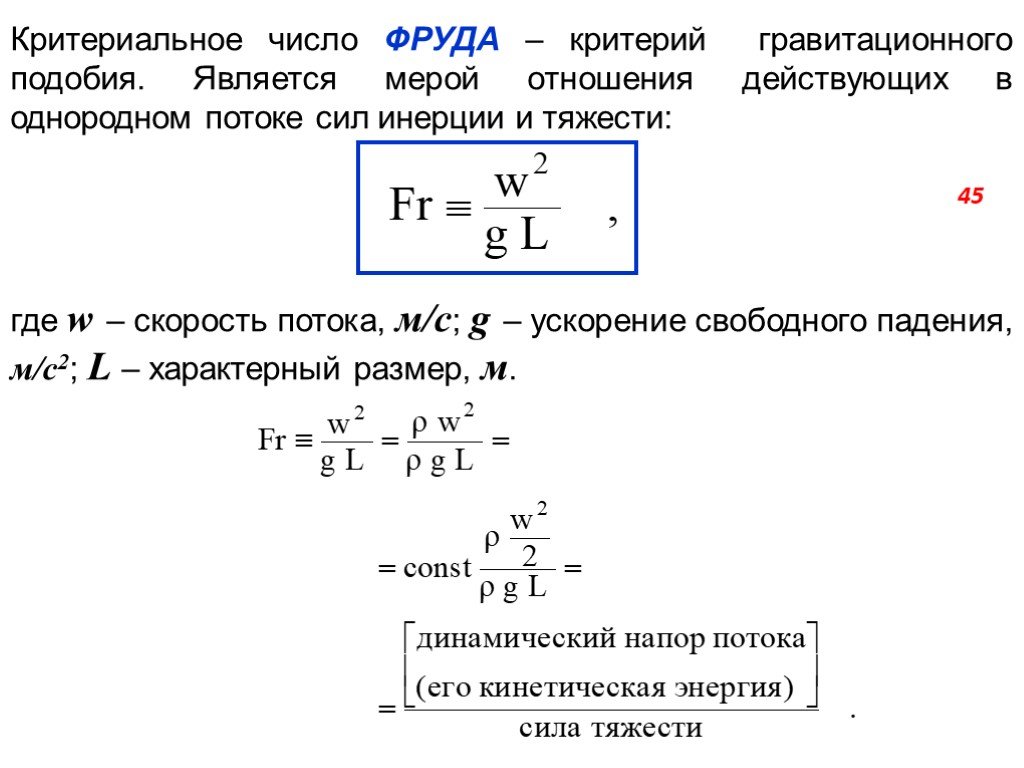
Слайд 45Критериальное число ФРУДА – критерий гравитационного подобия. Является мерой отношения действующих в однородном потоке сил инерции и тяжести: где w – скорость потока, м/с; g – ускорение свободного падения, м/с2; L – характерный размер, м.
Слайд 46Критериальное число ГАЛЛИЛЕЯ – критерий подобия полей свободного течения. Является мерой отношения сил тяжести и сил вязкого трения (молекулярного трения) в потоке. В форме критерия Архимеда, характеризует взаимодействие сил молекулярного трения и подъёмной силы, обусловленной разностью плотностей в изотермическом потоке. В форме критерия Грасгоффа – неизотермического. где L – характерный размер, м; g – ускорение свободного падения, м/с2; ν – кинематическая вязкость, м2/с.
Слайд 47Критериальное число АРХИМЕДА – характеризует взаимодействие сил молекулярного трения и подъёмной силы, обусловленной разностью плотностей в изотермическом потоке Является мерой отношения подъёмной силы, обусловленной разностью плотностей и силы вязкого трения: где L – характерный размер, м.
Слайд 48Критериальное число Рэлея – является мерой отношения подъёмных сил, обусловленных градиентом плотности, и сил вязкости . g ‒ ускорение свободного падения, м/с2; β ‒ коэффициент объёмного расширения, К‒1; ΔT ‒ разность температур, К; ν ‒ кинематический коэффициент вязкости, м2/с; L ‒ характерный размер, м; а ‒ коэффициент температуропроводности, м2/с.

Слайд 49Рэлей, Рейли (Rayleigh) Джон Уильям (12.11.1842, Лэнгфорд-Гров, графство Эссекс, — 30.6.1919, Тирлинг-Плейс, близ г. Уитем), английский физик, один из основоположников теории колебаний. Член Лондонского королевского общества (1873). Фамилия до получения титула лорда Рэлея (1873) — Стретт (Strutt). Окончил Кембриджский университет (1865); после смерти Дж. Максвелла (1879) стал профессором этого университета и директором Кавендишской лаборатории. С 1887 профессор Британского королевского института (Лондон). Диапазон научных интересов Р. очень широк: акустика, теория колебаний, оптика, электричество и другие области физики. Р. исследовал акустические колебания (колебания струн, стержней, пластинок и др.). В 1873 он сформулировал ряд фундаментальных теорем линейной теории колебаний, позволяющих делать качественные заключения о собственных частотах колебательных систем, и разработал количественный метод возмущений для нахождения собственных частот колебательной системы, мало отличающейся от простой системы с известными собственными частотами.

Слайд 50Рэлей впервые указал на специфичность нелинейных систем, способных совершать незатухающие колебания без периодического воздействия извне, и на особый характер этих колебаний (называемых впоследствии автоколебаниями). Он объяснил различие групповой и фазовой скоростей и получил формулу для групповой скорости (формула Рэлея). Он рассмотрел также задачу сложения многих колебаний со случайными фазами и получил функцию распределения для результирующей амплитуды — так называемое распределение Рэлея. Метод, разработанный при этом Рэлеем, надолго определил дальнейшее развитие теории случайных процессов. В теории упругих волн Рэлей рассмотрел вопросы дифракции, рассеяния и поглощения волн, давление звука, исследовал волны конечной амплитуды и особый вид поверхностных волн (волны Рэлея).

Слайд 51Работы Рэлея по теории колебаний систематизированы им в фундаментальном труде «Теория звука» (2 тт., 1877—78, 2 изд. 1894—96), в котором впервые отчётливо проявился единый подход к изучению колебательных и волновых процессов, имеющих различную природу. Эти идеи Рэлея легли в основу современной теории колебаний. В 1900 Рэлей вывел один из законов излучения абсолютно чёрного тела (закон Рэлея-Джинса); эта работа имела большое значение для возникновения теории квантов. Рэлей заложил основы теории молекулярного рассеяния света. Установив обратную пропорциональность интенсивности рассеянного света 4-й степени длины волны (закон Рэлея), он объяснил голубой цвет неба. В 1879 Р. создал теорию разрешающей способности оптических приборов. В 1894 совместно с У. Рамзаем открыл аргон. Имя Рэлея получили многие физические понятия, законы, приборы (диск Рэлея, интерферометр Рэлея, рэлеевское рассеяние света, закон Рэлея намагничения и др.). Нобелевская премия (1904).

Слайд 52Критериальное число Маха Критерий газодинамического подобия. Является мерой отношения скорости жидкости (теплоносителя) и скорости распространения в нём упругих деформаций (скорости звука). vfluid ‒ скорость жидкости, м/с. vsound ‒ скорость звука, м/с.
Слайд 53Критериальное число Эйлера – Критерий подобия полей давления. Мера отношения силы давления и инерционной силы в потоке: отношение перепада давления и кинетической энергии потока. Мера отношения перепада статического давления в потоке к динамическому напору потока – (ρW2/2). ΔР ‒ перепад давления, Па; ρ ‒ плотность теплоносителя, кг/м3; w ‒ скорость потока, м/с.
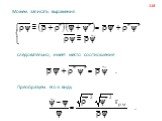
Слайд 54Это и есть искомое дифференциальное уравнение сохранения импульса, которое также называют уравнением движения в напряжениях, или первым законом Коши. Учитывая определение субстанциональной производной, выражение (61) сформулируем в виде (62) Умножив уравнение неразрывности (55) скалярно на вектор скорости и сложив с (62), получим (63) Введем в рассмотрение тензор дополнительных напряжений , который зададим так: (64)

Слайд 55Реологическое уравнение (реологический закон) ‒ уравнение, связывающее компоненты тензоров напряжений, деформаций и их производных по времени. Производная по времени от тензора деформаций называется тензором скоростей деформаций. Таким образом, реологическое уравнение ‒ это уравнение связывающее тензор напряжений с тензором скоростей деформаций. В зависимости от того, какое реологическое соотношение используется, принято выделять, как наиболее важные с методологической и практической точки зрения, следующие типы жидкостей: ● идеальная жидкость, ● ньютоновская жидкость, ● сильно реологическая жидкость.
Слайд 56Идеальная жидкость
Дифференциальное уравнение сохранения импульса (количества движения) ≡ ≡ Уравнение движения в напряжениях ≡ ≡ Первый закон Коши
Слайд 57
Слайд 58Ньютоновская жидкость Ньютоновской жидкостью называется жидкость, для которой справедливо следующее утверждение: тензор дополнительных напряжений линейно пропорционален градиенту вектора скорости. (*) Соотношение (*) называют обобщённым законом Ньютона для вязкой жидкости. Коэффициентом пропорциональности μ определяет внутреннее трение или, иначе говоря, вязкость жидкости по Ньютону. Эту величину принято также называть динамическим коэффициентом вязкости. Второе слагаемое учитывает эффекты сжимаемости. Величину ζ называют второй вязкостью. Если жидкость несжимаемая (а во многих случаях, в частности, при параметрах потока, характерных для задач реакторной теплофизики, и при рассмотрении жидкости как сжимаемой) вторым слагаемым пренебрегают. В этом случае тождество (*) принимает вид (обобщённый закон Ньютона для несжимаемой жидкости) (**)

Слайд 59Тождество (*) – реологическое уравнение ньютоновской жидкости. Тождество (**) – реологическое уравнение ньютоновской несжимаемой жидкости. Коэффициентом пропорциональности является внутреннее трение или, иначе говоря, вязкость жидкости по Ньютону. Эту величину (обычно обозначают μ) принято называть динамический коэффициент вязкости. Динамический коэффициент вязкости является функцией температуры: μ=μ(Т). В реальных жидкостях при очень больших давлениях динамический коэффициент вязкости – функция температуры и давления: μ=μ(Т, Р). Размерность: в СИ – [μ]=Па·с; в СГС – [μ]=пуаз. 1Па·с=10 Пуаз. Кинематический коэффициент вязкости – отношение динамического коэффициента вязкости к плотности: ν=μ/ρ. Размерность: в СИ – [ν]=м2/с; в СГС – [ν]=стокс.

Слайд 60Воспользовавшись тождеством (*) преобразуем записанное в дивергентной форме дифференциальное уравнение сохранения количества движения к виду (▼) Это так называемое полное уравнение Навье-Стокса – уравнение движения (синоним уравнение сохранения количества движения) ньютоновской сжимаемой жидкости.
Слайд 61Воспользовавшись тождеством (**) преобразуем записанное в дивергентной форме дифференциальное уравнение сохранения количества движения к виду (▼▼) Это так называемое уравнение Навье-Стокса – уравнение движения (синоним уравнение сохранения количества движения) ньютоновской НЕсжимаемой жидкости. Для стационарного движения (▼▼) принимает вид (▼▼▼)
Слайд 62Перейдя от субстанциональной производной к частным производным и использовав уравнение неразрывности (55), получим дивергентный вид дифференциального уравнения сохранения энергии в терминах энтальпии (85)
Слайд 63Ф – диссипативная функция:
Всегда Ф > 0. Следовательно, всегда часть тепла диссипирует.
Слайд 64
Слайд 65Хинце И.О., Турбулентность, пер. с англ., М., 1963. Монин А.С., Яглом А.М., Статистическая гидромеханика, ч. 1, М., 1965, ч. 2, М., 1967.
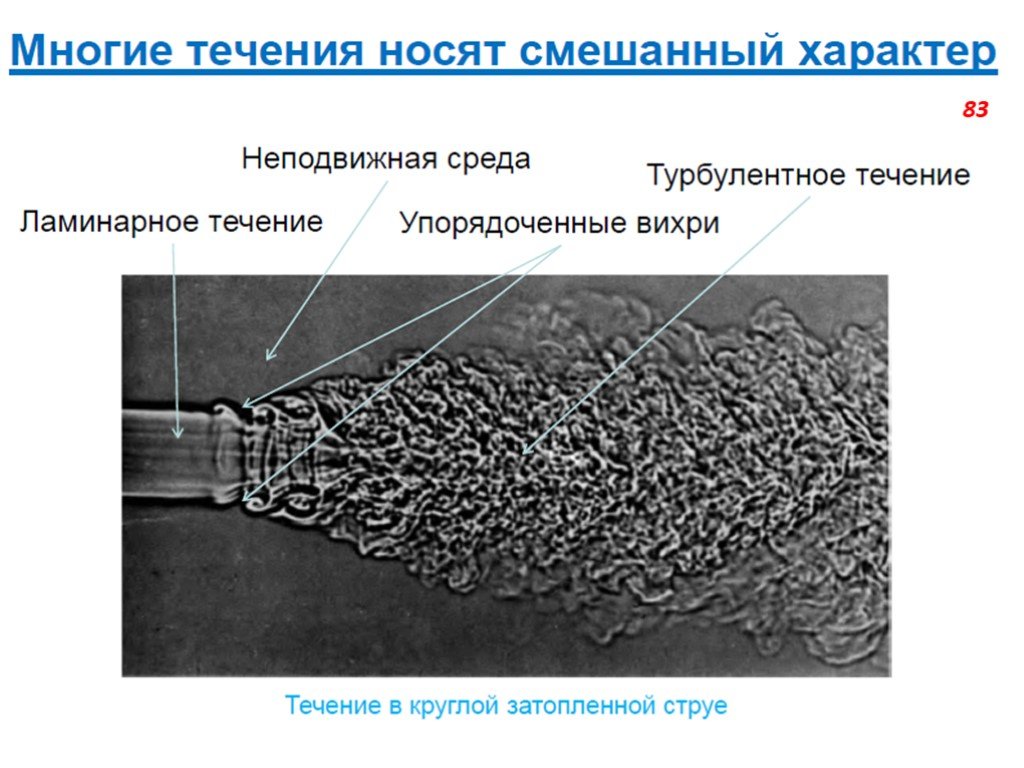
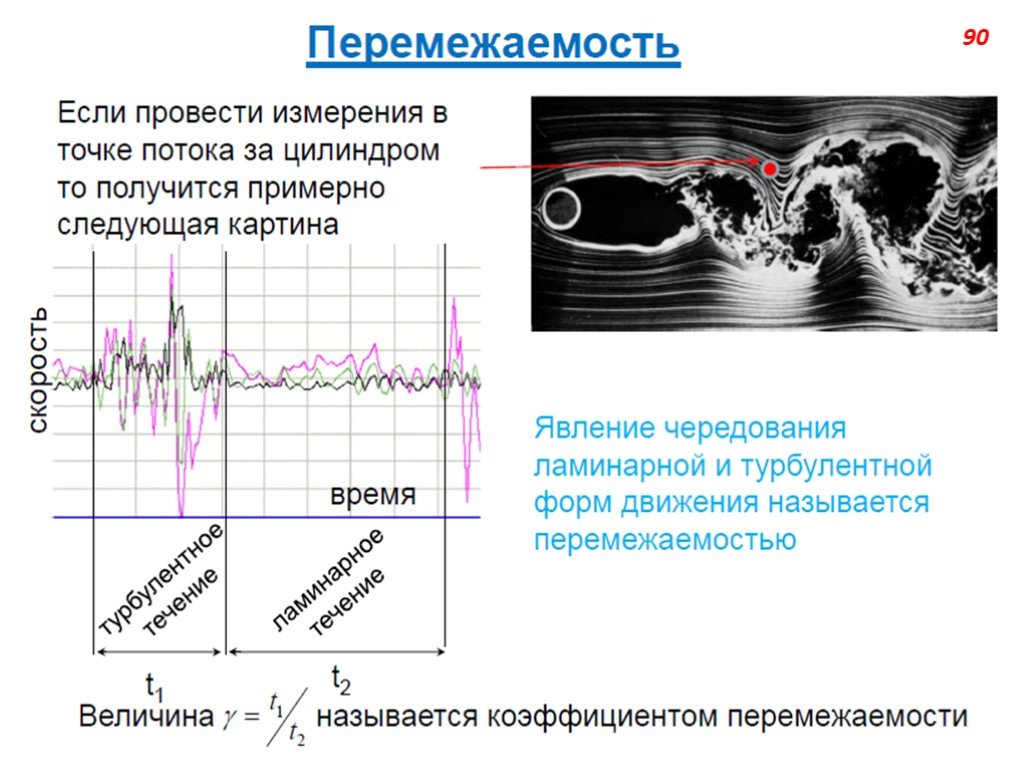
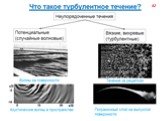
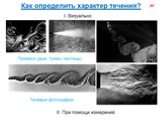
Слайд 66Ламинарное течение (от лат. lamina — пластинка), упорядоченное течение жидкости или газа, при котором жидкость (газ) перемещается как бы слоями, параллельными направлению течения. Ламинарные течения наблюдаются или у очень вязких жидкостей, или при течениях, происходящих с достаточно малыми скоростями, а также при медленном обтекании жидкостью тел малых размеров. В частности, ламинарные течения имеют место в узких (капиллярных) трубках, в слое смазки в подшипниках, в тонком пограничном слое, который образуется вблизи поверхности тел при обтекании их жидкостью или газом, и др. С увеличением скорости движения данной жидкости ламинарное течение может в некоторый момент перейти в неупорядоченное турбулентное течение. При этом резко изменяется сила сопротивления движению.

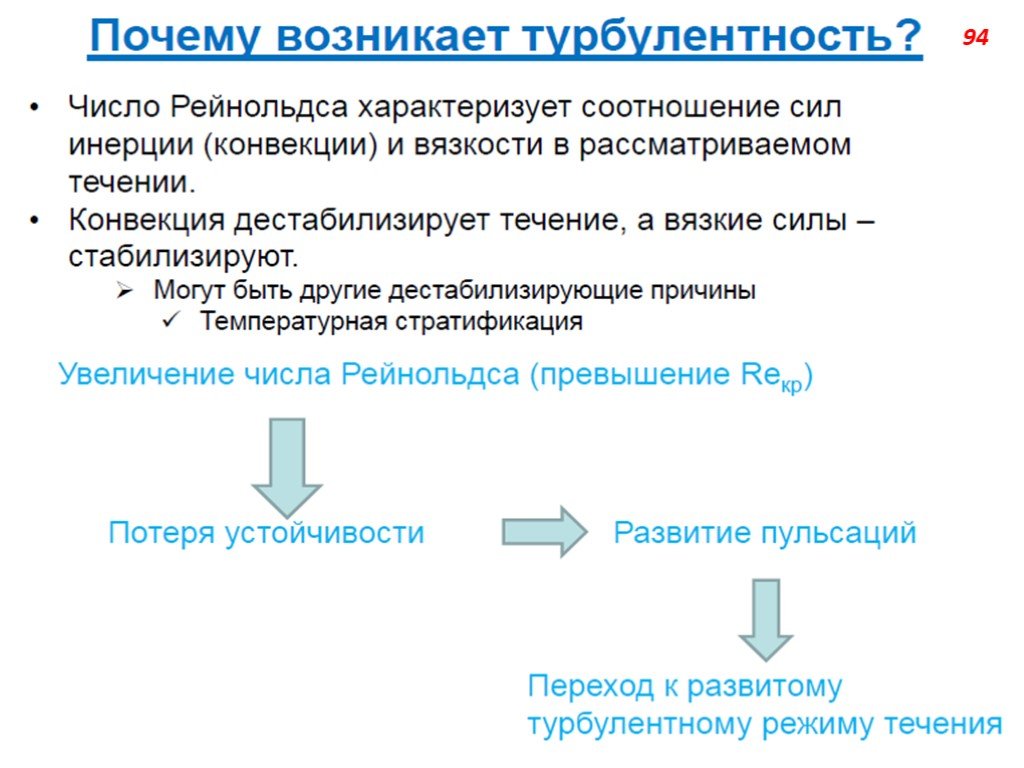
Слайд 67Режим течения жидкости характеризуется числом Рейнольдса. Когда значение меньше некоторого критического числа REкр, меет место ламинарное течение жидкости. Если RE ≥ REкр, режим течения может стать турбулентным. Значение зависит от вида рассматриваемого течения. Для течения в круглых трубах (если характерной скоростью считать среднюю по сечению скорость, а характерным размером – диаметр трубы) Reкр=2200. При Re

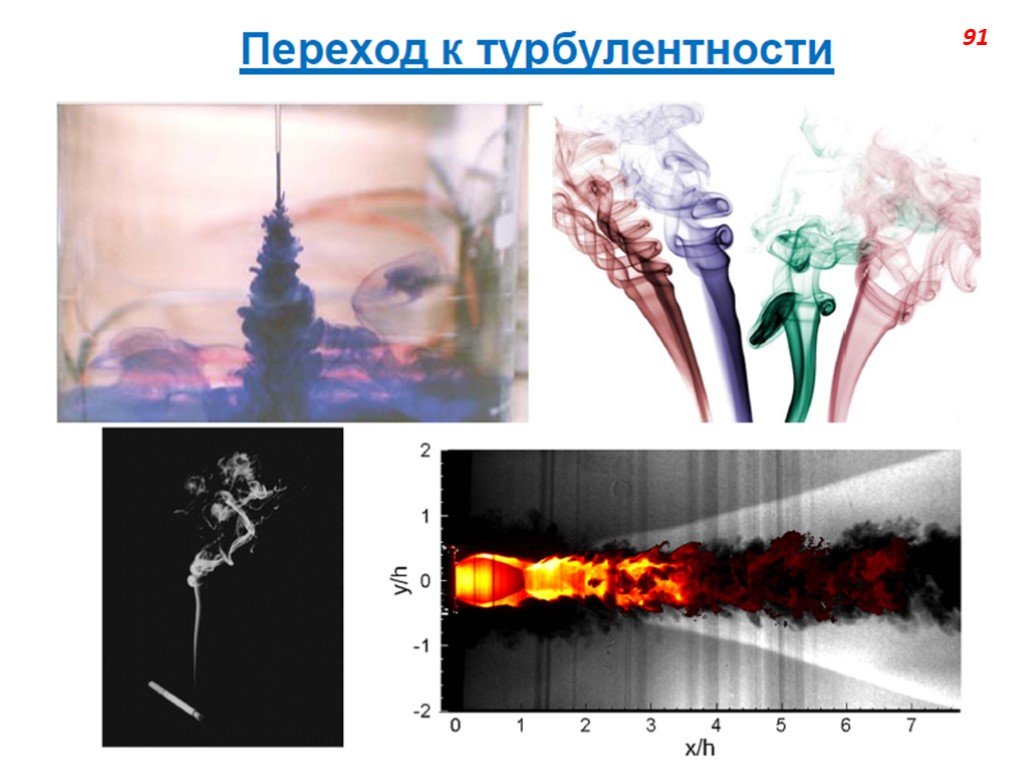
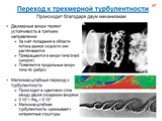
Слайд 68Наш мир устроен таким образом, что большинство течении, интересных с практической точки зрения, являются турбулентными. Рассмотрим, например, воздух. Вязкость ν=1.5·10–5 м2/с. Переход от ламинарного режима течения к турбулентному осуществляется, в зависимости от типа течения, при числе Рейнольдса Re=UL/ν~102÷105. Это означает, что переход происходит при произведении линейного масштаба на скоростной UL~10–3÷100 м2/с, что весьма немного. С физической точки зрения, причиной возникновения турбулентности является неустойчивость того или иного рода, возникающая в рассматриваемом течении (например, след за цилиндром или тепловая неустойчивость). Следует отметить, что во многих случаях появлению турбулентности предшествует появление упорядоченных нестационарных структур.

Слайд 69С математической точки зрения появление турбулентности (как решения уравнении Навье-Стокса), как правило, обусловлено доминированием дестабилизирующих конвективных членов над стабилизирующими вязкими членами в уравнении баланса импульса. В результате этого, уравнения Навье-Стокса, описывающие течения жидкости и газа, теряют устойчивость. При этом происходит лавинообразное накопление возмущений определенного вида. С третьей стороны, процесс потери устойчивости можно рассматривать как проявление второго начала термодинамики: природа не терпит слишком «упорядоченных» течений.

Слайд 70Потеря устойчивости ламинарным потоком – явление довольно тонкое, зависящее от большого количества внешних факторов, таких как уровень турбулентности внешнего потока, градиентов температур или давления, вдува-отсоса и т. п. (примеры: пограничный слой при наличии градиента давления, струя с внешним возмущением). Следует отметить, что при потере устойчивости колебания только начинают развиваться, полностью турбулентным течение становится гораздо позже (ниже по потоку), когда амплитуды пульсаций достигнут определенного уровня. Нелинейность газодинамических систем (с физической точки зрения) и описывающих их уравнений Навье-Стокса (с математической точки зрения) приводит к тому, что амплитуда возмущений оказывается ограниченной. Когда амплитуда возмущений достигает насыщения, часто говорят, что течение стало «развитым турбулентным».

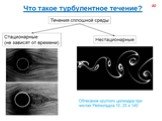
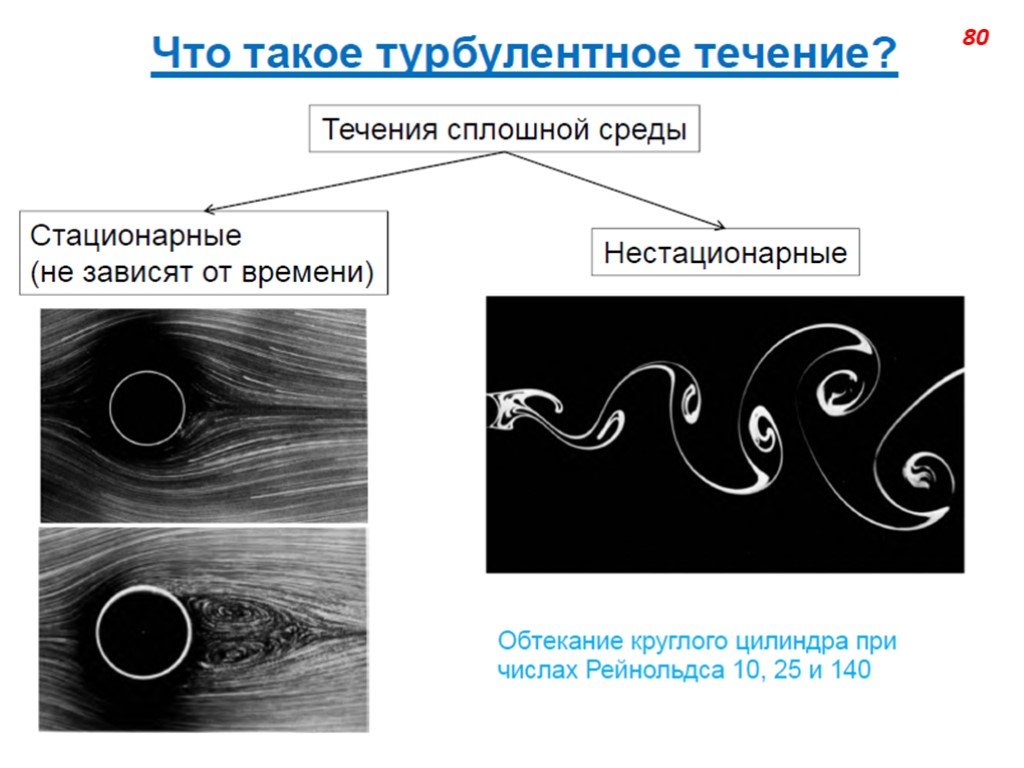
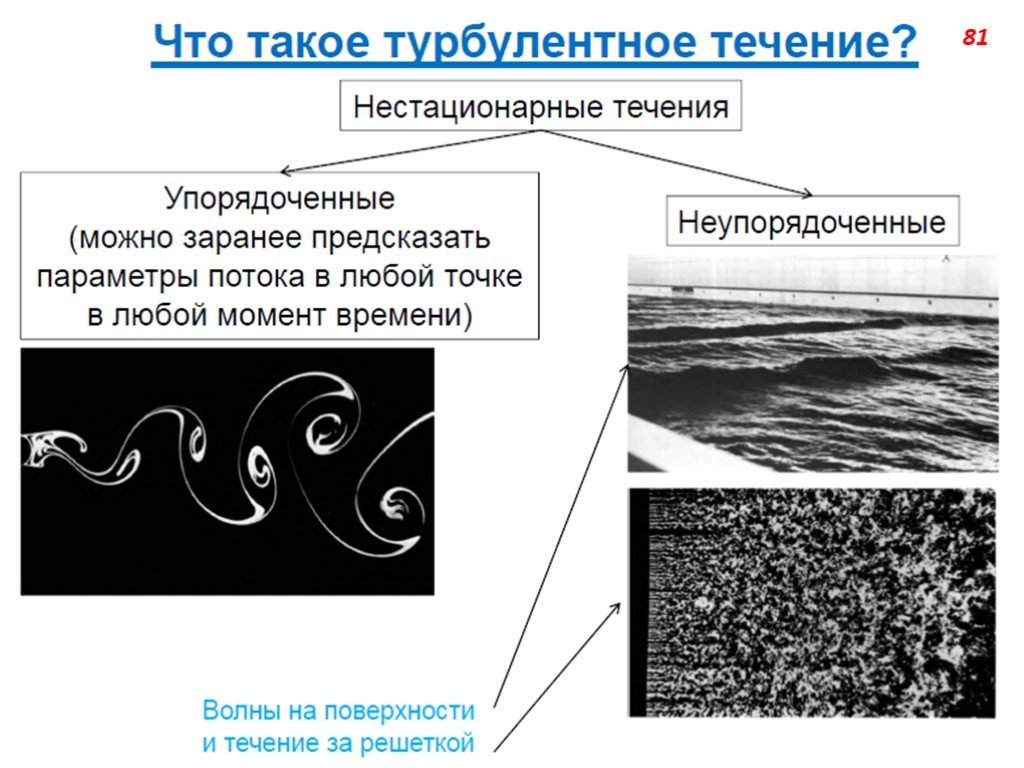
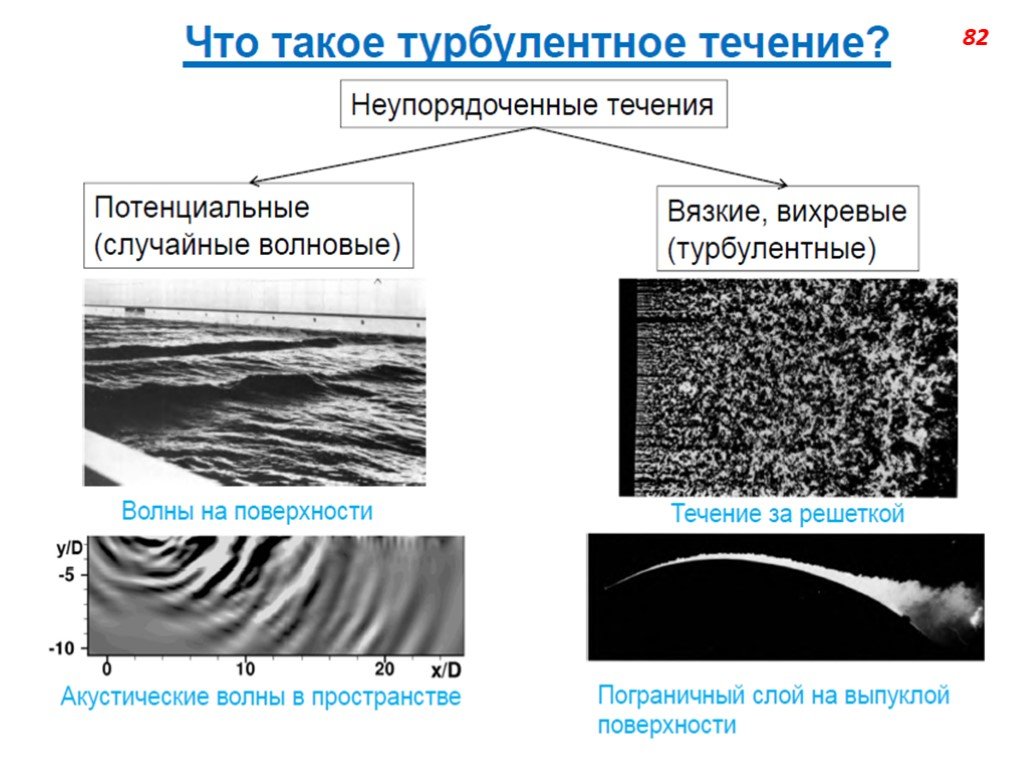
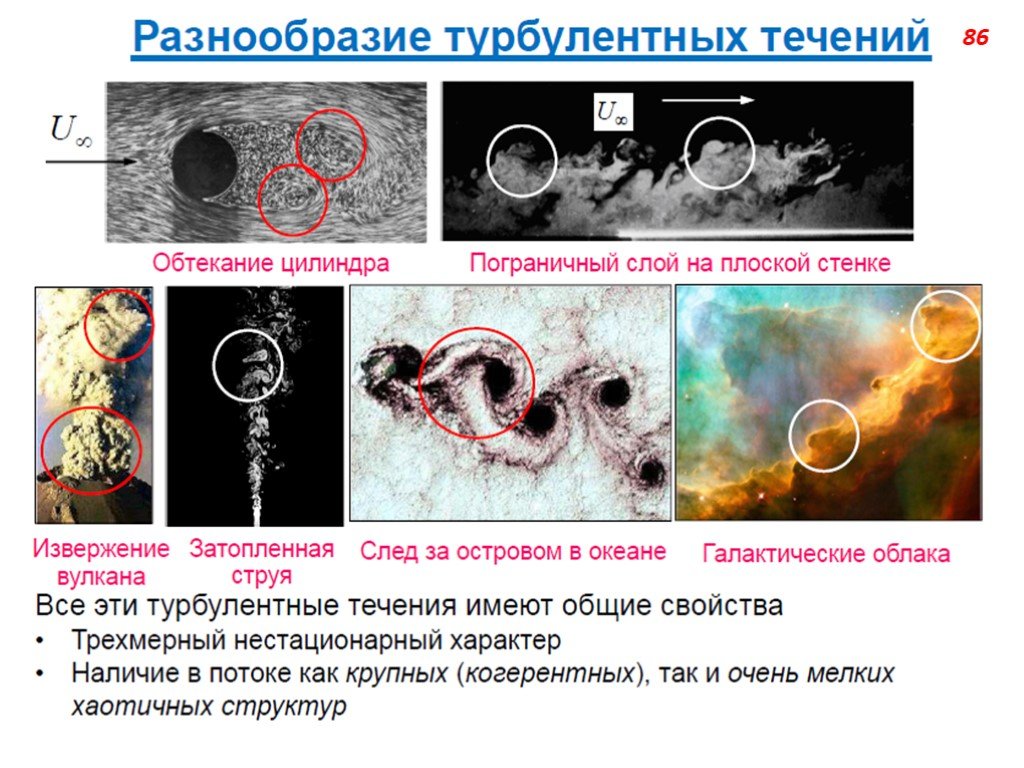
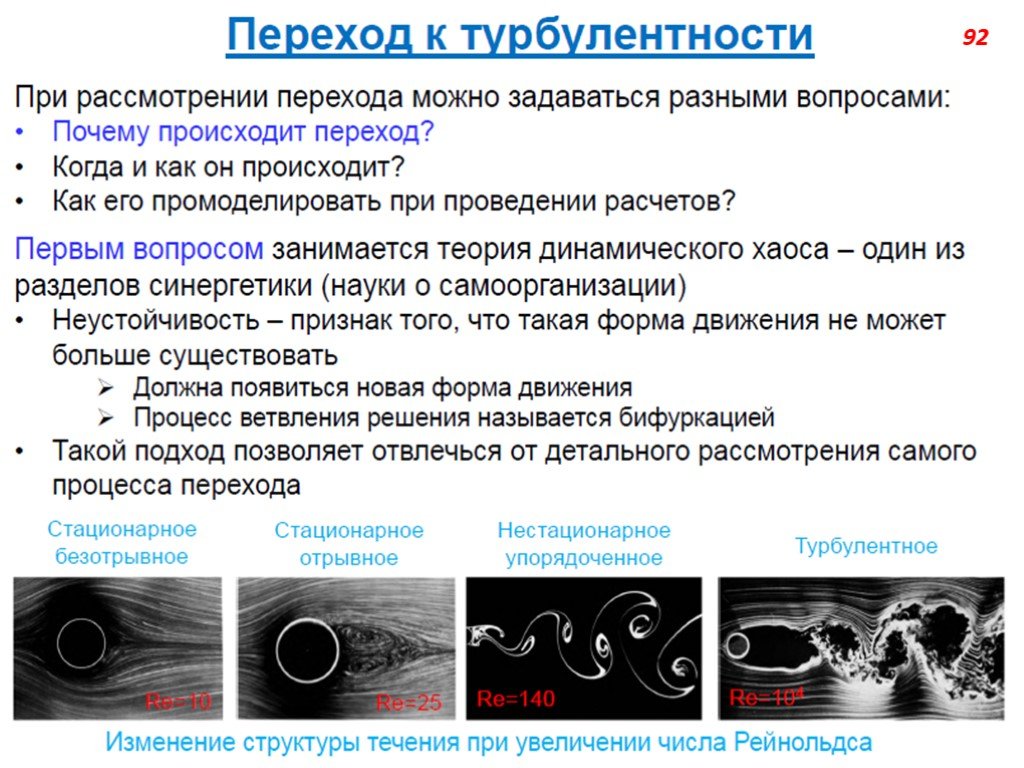
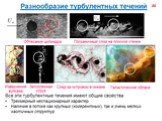
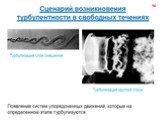
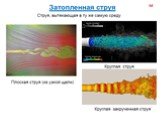
Слайд 71Турбулентность – явление, наблюдаемое во многих течениях жидкостей и газов и заключающееся в том, что в этих течениях образуются многочисленные вихри различных размеров, вследствие чего их гидродинамические и термодинамические характеристики (скорость, температура, давление, плотность) испытывают хаотические флуктуации и потому изменяются от точки к точке и во времени нерегулярно. Этим турбулентные отличаются от ламинарных. Большинство течений жидкостей и газов в природе (движение воздуха в земной атмосфере, воды в реках и морях, газа в атмосферах Солнца и звёзд и в межзвёздных туманностях и т.п.) и в технических устройствах (в трубах, каналах, струях, в пограничных слоях около движущихся в жидкости или газе твёрдых тел, в следах за такими телами и т.п.) оказываются турбулентными.

Слайд 72Благодаря большой интенсивности турбулентного перемешивания турбулентные течения обладают повышенной способностью к передаче количества движения (импульса). А потому к повышенному силовому воздействию на обтекаемые твёрдые тела), передаче тепла, ускоренному распространению химических реакций (в частности, горения), способностью нести и передавать взвешенные частицы, рассеивать звуковые и электромагнитные волны и создавать флуктуации их амплитуд и фаз, а в случае электропроводной жидкости – генерировать флуктуирующее магнитное поле и т.д.

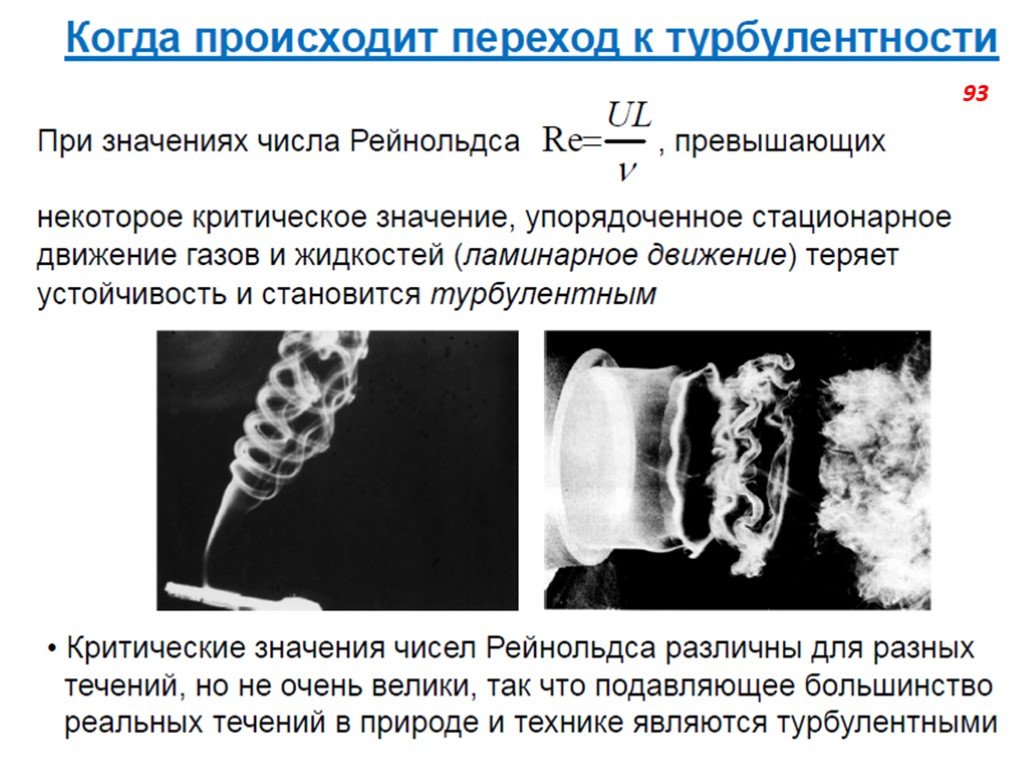
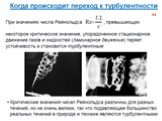
Слайд 73Турбулентность возникает вследствие гидродинамической неустойчивости ламинарного течения, которое теряет устойчивость и превращается в турбулентное, когда так число Рейнольдса превзойдёт некоторое критическое значение . По экспериментальным данным, в прямых круглых трубах при наибольшей возможной степени возмущённости течения у входа в трубу критическое число Рейнольдса равно 2300. Уменьшая степень начальной возмущённости течения, можно добиться затягивания ламинарного режима до значительно больших значений числа Рейнольдса. В трубах до 50 000.

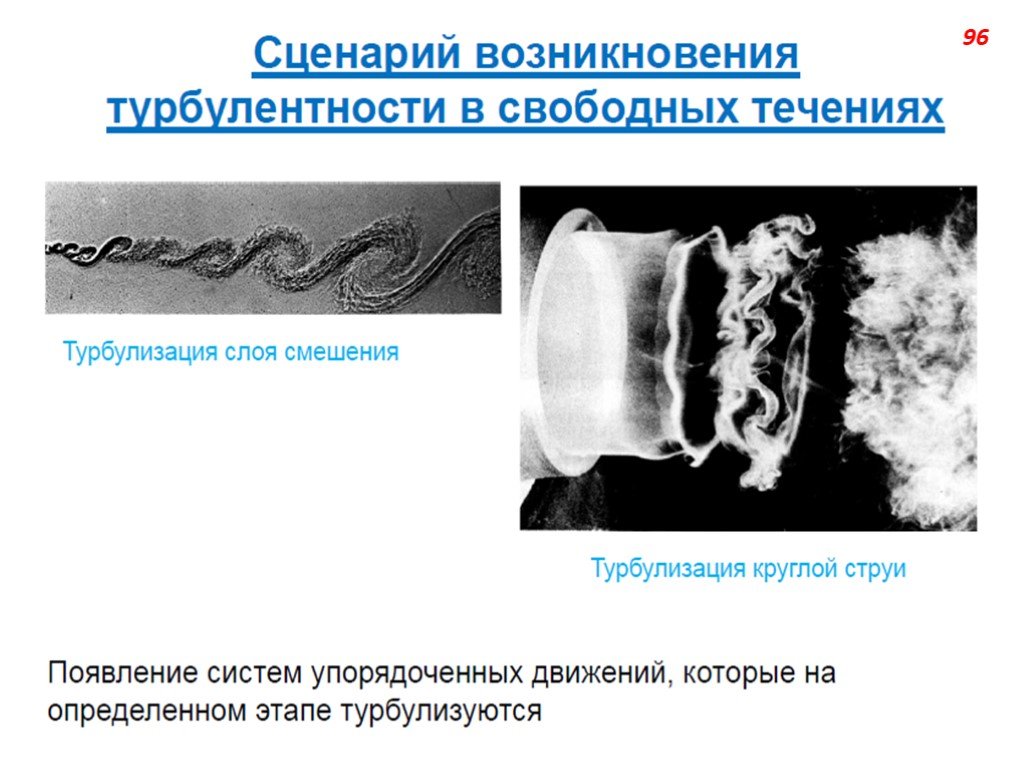
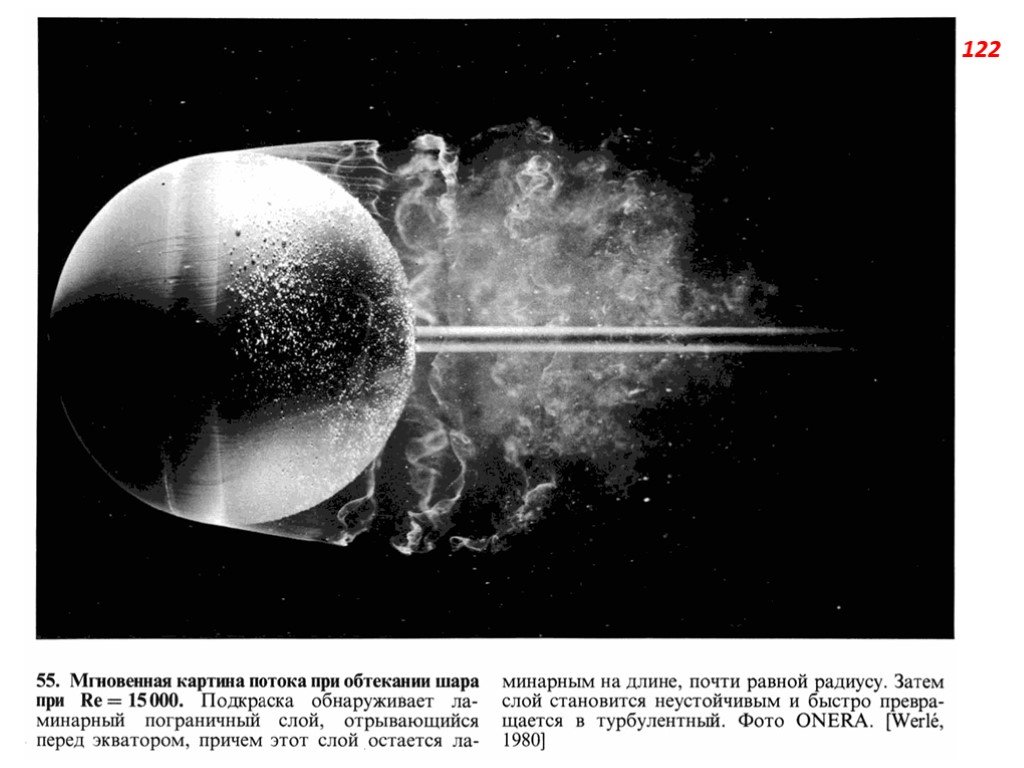
Слайд 74Возникновение турбулентности при обтекании твёрдых тел может проявляться не только в виде турбулизации пограничного слоя, но и в виде образования турбулентного следа за телом в результате отрыва пограничного слоя от его поверхности. Турбулизация пограничного слоя до точки отрыва приводит к резкому уменьшению полного коэффициента сопротивления тела. Турбулентность может возникнуть и вдали от твёрдых стенок, как при потере устойчивости поверхности разрыва скорости (например, образующейся при отрыве пограничного слоя или являющейся границей затопленной струи или поверхностью разрыва плотности), так и при потере устойчивости распределения плотностей слоев жидкости в поле тяжести, то есть при возникновении конвекции. Критическое число Рэлея имеет значение около 1100÷1700.

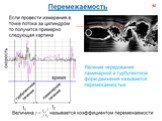
Слайд 75Вследствие чрезвычайной нерегулярности гидродинамических полей турбулентных течений применяется статистическое описание турбулентности: гидродинамические поля трактуются как случайные функции от точек пространства и времени, и изучаются распределения вероятностей для значений этих функций на конечных наборах таких точек. Наибольший практический интерес представляют простейшие характеристики этих распределений: средние значения и вторые моменты гидродинамических полей, в том числе дисперсии компонент скорости; компоненты турбулентного потока количества движения (так называемое напряжения Рейнольдса) и турбулентного потока тепла. Статистические моменты гидродинамических полей турбулентного потока должны удовлетворять некоторым уравнениям (вытекающим из уравнений гидродинамики), простейшие из которых — так называемые уравнения Рейнольдса, получаются непосредственным усреднением уравнений гидродинамики. Однако точного решения их до сих пор не найдено, поэтому используются различные приближённые методы.

Слайд 76Основной вклад в передачу через турбулентную среду количества движения и тепла вносят крупномасштабные компоненты турбулентности (масштабы которых сравнимы с масштабами течения в целом); поэтому их описание — основа расчётов сопротивления и теплообмена при обтекании твёрдых тел жидкостью или газом. Для этой цели построен ряд так называемых полуэмпирических теорий турбулентности, в которых используется аналогия между турбулентным и молекулярным переносом, вводятся понятия пути перемешивания, интенсивности турбулентности, коэффициента турбулентной вязкости и теплопроводности и принимаются гипотезы о наличии линейных соотношений между напряжениями Рейнольдса и средними скоростями деформации, турбулентным потоком тепла и средним градиентом температуры. Такова, например, применяемая для плоскопараллельного усреднённого движения формула Буссинеска с коэффициентом турбулентного перемешивания (турбулентной вязкости) , который, в отличие от коэффициента молекулярной вязкости, уже не является физической постоянной жидкости, а зависит от характера усреднённого движения.

Слайд 77Большую роль в полуэмпирических теориях играют гипотезы подобия. В частности, они служат основой полуэмпирической теории Кармана. А.Н. Колмогоров предложил использовать в полуэмпирических теориях гипотезу подобия, по которой характеристики турбулентности выражаются через её интенсивность и масштаб (например, скорость диссипации энергии e ~ b3/ l). Одним из важнейших достижений полуэмпирической теории турбулентности является установление универсального (по числу Рейнольдса, при больших Re) логарифмического закона для профиля скорости в трубах, каналах и пограничном слое.

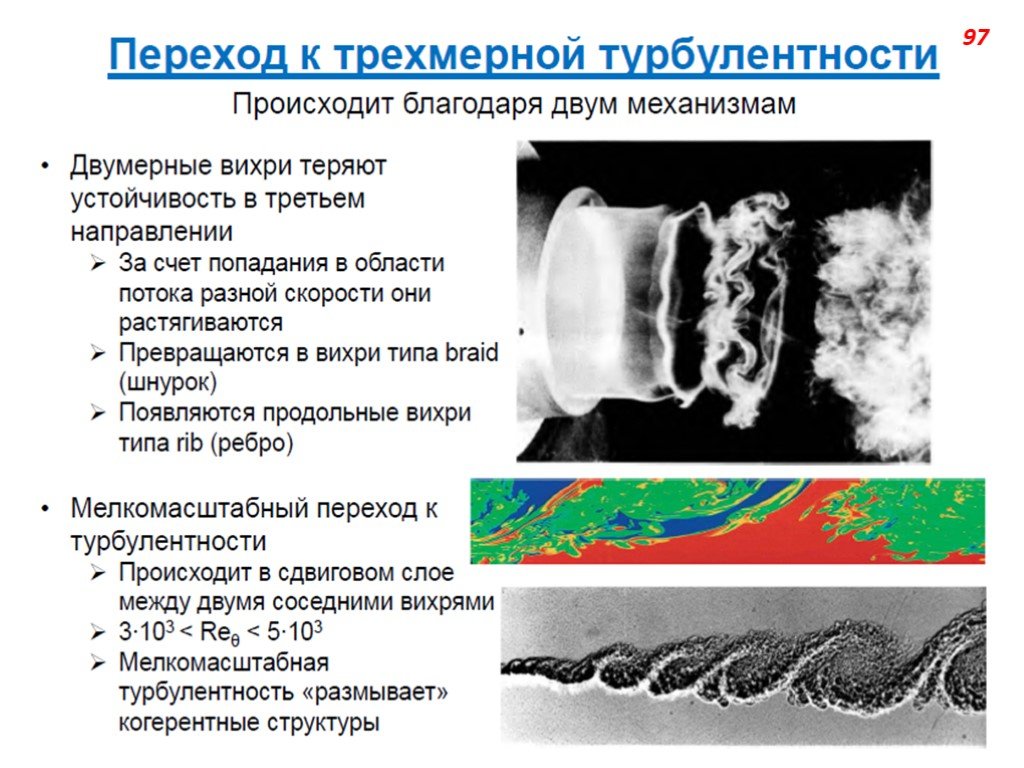
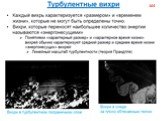
Слайд 78Мелкомасштабные компоненты турбулентности (масштабы которых малы по сравнению с масштабами течения в целом) вносят существенный вклад в ускорения жидких частиц и в определяемую ими способность турбулентного потока нести взвешенные частицы, в относительное рассеяние частиц и дробление капель в потоке, в перемешивание турбулентных жидкостей, в генерацию магнитного поля в электропроводной жидкости, в спектр неоднородностей электронной плотности в ионосфере, в флуктуации параметров электромагнитных волн, в болтанку летательных аппаратов и т.д.

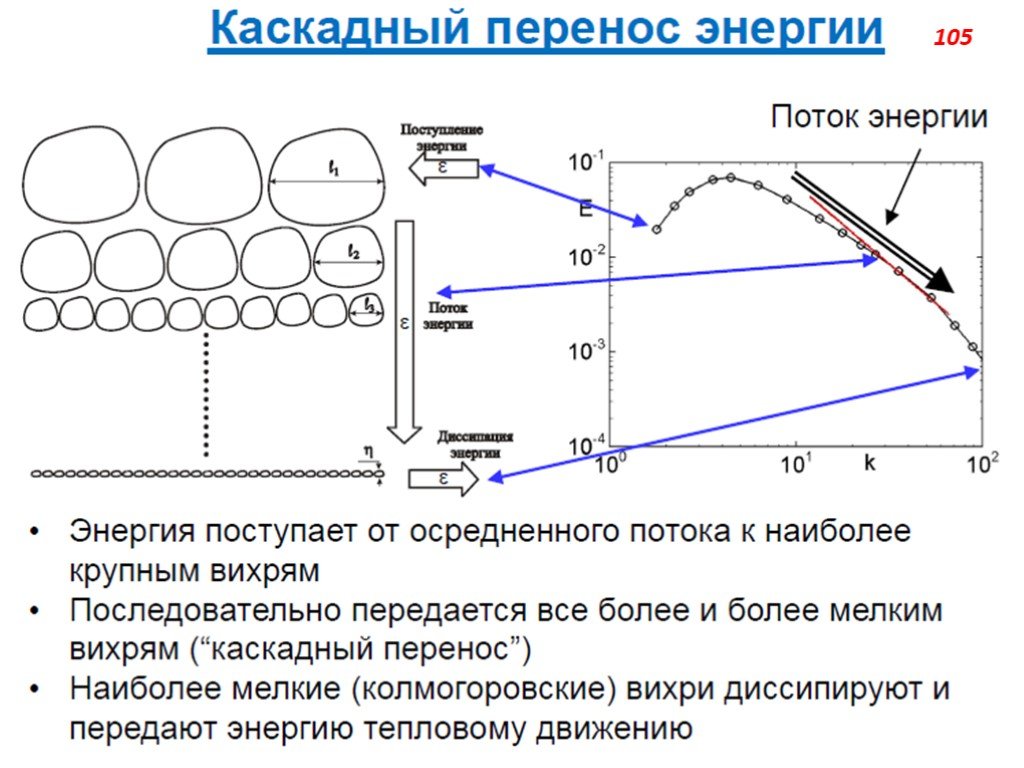
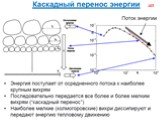
Слайд 79Описание мелкомасштабных компонент турбулентнос-ти базируется на гипотезах Колмогорова, основанных на представлении о каскадном процессе передачи энергии от крупномасштабных ко всё более и более мелкомасштабным компонентам турбулентности. Вследствие хаотичности и многокаскадности этого процесса при очень больших числах Рейнольдса режим мелкомасштабных компонент оказывается пространственно-однородным, изотропным и квазистационарным и определяется наличием среднего притока энергии от крупномасштабных компонент и равной ему средней диссипации энергии в области минимальных масштабов. По первой гипотезе Колмогорова, статистические характеристики мелкомасштабных компонент определяются только двумя параметрами. По второй гипотезе, при очень больших Re в мелкомасштабной области существует такой (так называемый инерционный) интервал масштабов, больших по сравнению с, в котором параметр оказывается несущественным, так что в этом интервале характеристики турбулентность определяются только одним параметром .
Слайд 80
Слайд 81
Слайд 82
Слайд 83
Слайд 84
Слайд 85
Слайд 86
Слайд 87
Слайд 88
Слайд 89
Слайд 90
Слайд 91
Слайд 92
Слайд 93
Слайд 94
Слайд 95
Слайд 96
Слайд 97
Слайд 98
Слайд 99
Слайд 100Характеристики турбулентности Несмотря на простое определение, сводящееся к понятию «случайных пульсаций», турбулентность имеет чрезвычайно сложную природу. Причина турбулентных пульсаций связана с неустойчивостью потока в целом, и их масштаб определяется балансом воздействии различной природы. На первый взгляд абсолютно «случайный процесс», тем не менее, подчиняется неким закономерностям, которые можно извлечь при помощи разных подходов (в первую очередь математических). Введем основные понятия, которые используются для описания свойств турбулентности.

Слайд 101Часто используется понятие «турбулентного вихря», а турбулентность определяют как совокупность разномасштабных вихрей. Можно показать, что в несжимаемой жидкости вихрь с любым распределением угловой скорости удовлетворяет уравнению неразрывности. Это означает, что турбулентное движение несжимаемой жидкости может быть представлено в виде суперпозиции различных вихрей. Популярность использования термина «турбулентный вихрь» (кроме причин исторического характера, связанных с гипотезой пути смешения Прандтля) обусловлена тем, что при визуализации турбулентных течении эти «вихри» видны и хорошо различимы. Максимальный размер вихрей близок к характерному линейному масштабу задачи L. Примеры: пограничный слой, профиль под углом атаки. Часто движение наиболее крупных вихрей оказывается в значительной степени упорядоченным (например, течение за цилиндром). Такие структуры часто называют когерентными.

Слайд 102Вихри минимального размера диссипируют непосредственно в тепло. Их размер характеризуется так называемым колмогоровским масштабом: ηk=(ν3/)1/4, где – местная скорость диссипации на единицу массы, a v – кинематическая вязкость. Наибольшее количество энергии при этом переносят вихри некоторого «среднего» размера. Часто пользуются понятиями «характерный размер» и «характерное время жизни» турбулентного вихря. Если при этом не конкретизируется, какие именно вихри имеются ввиду, чаше всего эти понятия относятся именно к «средним» наиболее «энергонесущим» вихрям.
Слайд 103
Слайд 104
Слайд 105
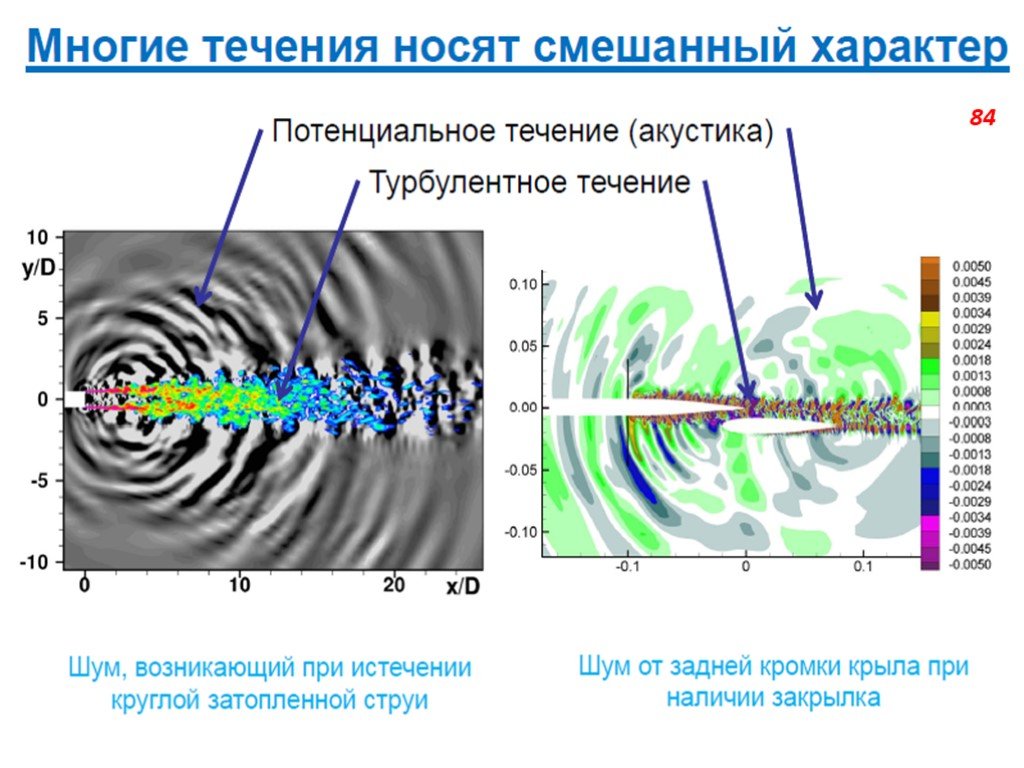
Слайд 106С практической точки зрения в большинстве случаев основной интерес представляют не актуальные величины, а усреднённые характеристики. Например, подъёмная сила крыла, коэффициент потерь в турбине, сопротивление планёра самолёта. Однако бывают задачи, в которых существенный интерес представляют именно пульсации. Например, задачи аэроакустика и аэроупругости. Именно поэтому большое развитие получила статистическая теория турбулентности, которая основана на аппарате математической статистики (теории вероятностей). Другой общепринятый подход в значительной мере базируется на использовании экспериментальных данных и называется полуэмпирической теорией турбулентности. Кроме того, существует значительное количество менее значимых с практической точки зрения подходов (например, основанных на теории хаоса).
Слайд 107
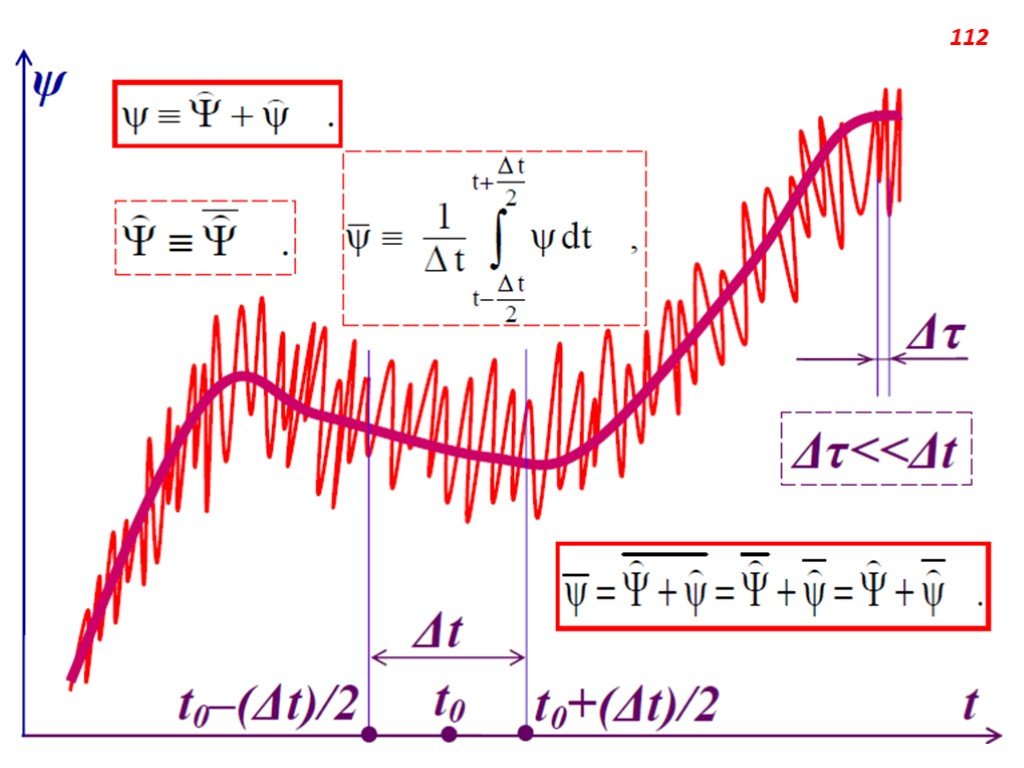
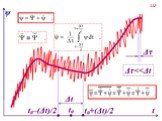
Слайд 108При описании турбулентного потока используются, как предложено Рейнольдсом, усреднённые по времени уравнения сохранения. При этом интервал усреднения выбирается достаточно большим по сравнению с характерным временем турбулентных пульсаций. Турбулентная величина ,являющаяся функцией координат и времени представляется , как сумма макроскопической составляющей и флуктуации :
Слайд 109Среднее значение турбулентной величины определяется следующим образом:
Очевидно, что
Слайд 110Для средних значений справедливы также следующие соотношения
Полагаем, что макроскопическая составляющая равна своему среднему значению:
Слайд 111Из этого НЕ следует равенство среднего значения турбулентной величины и среднего значения её макроскопической составляющей:
Существуют два метода определения макроскопических составляющих. В обоих макроскопическая составляющая плотности полагается равной среднему значению плотности:
Слайд 112
Слайд 113Если в качестве макроскопической составляющей выбрано среднее значение величины, условимся флуктуационную составляющую обозначать двумя штрихами вверху:
Можем записать: получим
Аналогичное представление используется для давления:
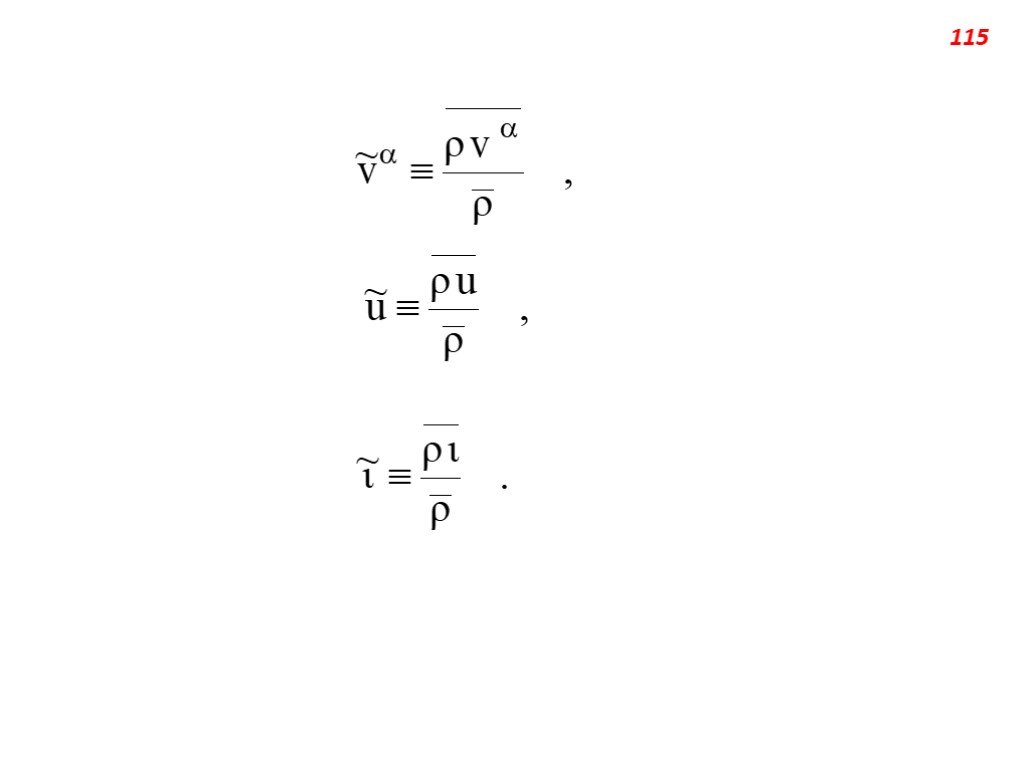
Слайд 114Макроскопические составляющие скорости и энергии (энтальпии) могут быть представлены таким же образом (этот метод усреднения назовем первым), либо как массово взвешенные величины. Второй метод, который применяется в данной работе, позволяет избавиться в усреднённых уравнениях сохранения от членов, содержащих усреднённый массовый поток, обусловленный турбулентностью. Флуктуацию турбулентной величины в этом случае будем обозначать одним штрихом вверху:
Таким образом, для скорости, внутренней энергии и энтальпии можем записать, соответственно, следующие выражения:
Слайд 115
Слайд 116Заметим, что в этом случае
Слайд 117Для несжимаемой жидкости
и, следовательно, для некоторой турбулентной величины
справедливы тождества
то есть для несжимаемой жидкости оба метода усреднения эквивалентны.
Слайд 118Можем записать выражения
следовательно, имеет место соотношение
Преобразуем его к виду
Слайд 119– коэффициент корреляции между величинами
Таким образом, справедливо соотношение
из которого следует, что оба метода усреднения эквивалентны, когда все коэффициенты корреляции равны нулю.
Слайд 120
Слайд 121
Слайд 122
Слайд 123
Слайд 124
Слайд 125Так как для сжимаемой жидкости применение второго метода усреднения позволяет, как уже отмечалось, исключить ряд членов в уравнениях сохранения, а также делает более ясной физическую интерпретацию получаемых усреднённых уравнений, далее рассмотрим второй метод усреднения.
Слайд 126Дифференциальные уравнения сохранения для турбулентного режима течения.
Усреднённое по времени уравнение неразрывности.
Усреднённое по времени уравнение сохранения импульса.
тензор турбулентных напряжений
Слайд 127Усреднённое по времени уравнение сохранения энергии.
‒ виртуальная энтальпия.
Слайд 128вектор турбулентной теплопроводности
‒ виртуальная внутренняя энергия
‒ кинетическая энергия турбулентности.

Слайд 129Влияние турбулентности на усреднённое течение Свойства турбулентных течений существенно отличаются от свойств ламинарных течений. Например, подъёмная сила одного и того же крыла при ламинарном и турбулентном обтекании может отличаться в разы. Поэтому необходимо тем или иным способом учитывать влияние турбулентности, то есть моделировать её. Результаты расчётов течений существенно зависят от качества моделирования турбулентности. Механизм влияния турбулентности на усреднённое течение связан с наличием турбулентного переноса всех газодинамических характеристик (импульса, энергии, температуры, концентрациии и т. п.). Если в ламинарном течении диффузионный перенос осуществляется при помощи броуновского движения, то в турбулентном «вихри» «перемешивают» среду, что существенно (в разы, а часто и на порядки) увеличивает скорость диффузионного переноса. С точки зрения актуального движения этот перенос имеет конвективную природу, однако с точки зрения усредненного движения он рассматривается как диффузионный.

Слайд 130
Слайд 131
Слайд 132
Слайд 133
Слайд 134
Слайд 135
Слайд 136
Слайд 137

Слайд 138Классификация моделей Для определения турбулентных напряжений используются модели турбулентности - алгебраические или дифференциальные соотношения. Моделей очень много, но ни одна из них не является идеальной. Причина такого многообразия - отсутствие идеальности и поиски новых, более точных или универсальных моделей. Спектр моделей турбулентности очень широк: от простых алгебраических связей до сложных моделей рейнольдсовых напряжений, содержащих 7 и более дифференциальных уравнений. Однако среди всего многообразия моделей можно выделить несколько основных групп (обсуждение основных групп моделей и их краткая характеристика): 1. Алгебраические модели; 2. Модели с одним дифференциальным уравнением; 3. Модели с двумя дифференциальными уравнениями; 4. Модели, не использующие гипотезу Буссинеска. Следует отметить, что некоторые модели формально невозможно отнести ни к одной из перечисленных категорий, эти модели мы будем рассматривать вместе с моделями, наиболее близкими к ним по свойствам.

Слайд 139МОДЕЛИ ГРАДИЕНТНОГО ТИПА Многие модели турбулентности, используемые в расчётной практике, основаны на концепции вихревой вязкости и турбулентной диффузии. Следуя Буссинеску, рейнольдсовые напряжения определяются как произведение вихревой вязкости на составляющие тензора осредненных скоростей деформации: (m1) Само по себе уравнение (m1) не вводит модели турбулентности, а только характеризует структуру такой модели, при этом основной задачей является задание функции νt. В отличие от коэффициента молекулярной вязкости v коэффициент νt определяется состоянием турбулентности и не связан со свойствами жидкости. Он может сильно изменяться от точки к точке пространства и в зависимости от типа течения. Так, например, vt в зонах циркуляционного течения может на несколько порядков превышать ν. Также известно, что для течения в открытом канале vt распределен по параболическому закону по глубине, а для плоской струи он изменяется пропорционально квадратному корню из расстояния от источника.

Слайд 140Иногда при расчётах турбулентных течений vt принимается постоянным (Буссинеск (1877), Васильев (1971)). Однако столь грубое описание турбулентности допустимо в тех случаях, когда величина турбулентного переноса не имеет существенного значения или использование более сложных конструкций представляется неоправданным. Концепция турбулентной вязкости предполагает, что перенос количества движения происходит аналогично переносу за счет молекулярного движения. Подвергаясь справедливой критике как физически необоснованная, она, однако, широко применяется, поскольку позволяет получать вполне приемлемые результаты в инженерной практике. Полезно представление о пропорциональности vt масштабу скорости U и масштабу турбулентности L, то есть vt~ U L (m2) поскольку для многих течений можно аппроксимировать с достаточной точностью распределение характерных масштабов.

Слайд 141По прямой аналогии с турбулентным переносом количества движения понятие турбулентной диффузии предполагает следующее соотношение между переносом массы или тепла и градиентом переносимой субстанции: (m3) где Dt – коэффициент турбулентной диффузии. Подобно турбулентной вязкости Dt не является собственной характеристикой жидкости, а зависит от состояния турбулентности. Согласно гипотезе Рейнольдса об аналогии при турбулентном переносе массы или тепла и количества движения, Dt = vt /Sct (m4) Величина Sct называется турбулентным числом Шмидта. В отличие от самих коэффициентов турбулентной диффузии (Dt) и турбулентной вязкости (vt), их отношение – Sct – слабо изменяется как в пределах потока, так и от течения к течению. Поэтому оно принимается постоянным в ряде моделей, хотя и испытывает влияние плавучести и кривизны линий тока.

Слайд 142Понятие турбулентной вязкости имеет недостатки. Это прежде всего касается ситуаций, когда в течениях возникают зоны отрицательной вязкости. К тому же предположение об изотропности коэффициентов турбулентной вязкости (диффузии) является сильным упрощением, имеющим ограниченную пригодность при интерпретации сложных течений, в частности тех, для которых действие массовых сил имеет преобладающее направление. Поэтому иногда коэффициенты турбулентной вязкости (диффузии) принимаются различными по разным направлениям.

Слайд 143Важными достоинствами моделей турбулентной вязкости являются их относительная простота, наглядность и вычислительная эффективность: в рамках приближения Буссинеска проблема замыкания сводится к определению одной скалярной величины (турбулентной вязкости) вместо 6 компонент тензора t. Во многих случаях, особенно при анализе течений, в которых основное влияние на усредненное движение оказывает лишь одна из компонент тензора рейнольдсовых напряжений (напряжение сдвига tху), нарушение гипотезы Буссинеска не приводит к сколько-нибудь заметным погрешностям. Указанные обстоятельства (относительная простота и приемлемость для широкого круга сдвиговых турбулентных течений) обусловливают широкую применимость моделей турбулентной вязкости. Более сложным подходом к решению проблемы замыкания является использование различных нелинейных соотношений между тензором анизотропии и тензором скоростей деформаций и составляющими вектора завихрённости, характеризующими кинематику усреднённого течения. Построенные на указанных принципах модели называются нелинейными моделями турбулентной вязкости. Впервые такой подход был предложен Поупом (1975), а в дальнейшем получил развитие в работах Спезайла (Speziale).

Слайд 144АЛГЕБРАИЧЕСКИЕ МОДЕЛИ ТУРБУЛЕНТНОСТИ Алгебраические модели принадлежат к простейшим типам моделей турбулентности, в которых связь между турбулентной вязкостью и параметрами усреднённого потока задается алгебраическими соотношениями. Отсюда следуют достоинства моделей такого типа: вычислительная эффективность, простота калибровки и модификаций с учётом специфики рассматриваемых течений. Однако очевидна и узкая специализация этих моделей, поскольку они опираются на априорную (эмпирическую) информацию о структуре конкретного рассматриваемого течения. Расширенное использование алгебраических моделей для других типов течений подчас невозможно в принципе (поскольку, например, опираясь на структурные кинематические характеристики пограничного слоя, такие как толщина вытеснения и потери импульса, скорость на внешней границе пограничного слоя, нельзя анализировать течения, для которых указанные характеристики не определены). Кроме того, алгебраическая формулировка моделей обусловливает их мгновенную реакцию на изменения параметров и условий на границах пограничного слоя. Тем не менее, алгебраические модели турбулентной вязкости многие десятилетия были (а во многих областях остаются) основным инструментом расчёта турбулентных сдвиговых течений.

Слайд 145Модель пути смешения Прандтля Модель для описания распределения νt впервые была предложена Л. Прандтлем в 1925 году и известна как модель пути смешения. Доказано, что она довольно хорошо воспроизводит тонкие вязкие слои. Рассматривая усредненные сдвиговые течения без градиента давления, Прандтль постулировал, что характерный масштаб пульсаций скорости v’ равен градиенту усреднённой скорости, умноженному на характерный масштаб длины lт, который он назвал путем смешения. Получим выражения коэффициентов турбулентной вязкости и турбулентной теплопроводности. Возьмем два слоя жидкости на расстоянии lm друг от друга (среднее расстояние пульсаций). Истинные скорости в этом случае (m5)

Слайд 146Вследствие пульсаций составляющей скорости v’y имеет место турбулентное перемешивание (перенос количества движения и тепла). Действительно, через единичную площадку, перпендикулярную оси у, в единицу времени переносится масса жидкости ρv’y. Находясь в первом слое, она имела количество движения . Во втором слое ее количество движения стало Таким образом, вследствие наличия пульсаций изменение количества движения обусловливает напряжение турбулентного трения (m6) Путь смешения (или перемешивания) lm определяется таким образом, чтобы (m7) Предполагая v’x ~ v’y , получаем

Слайд 147Следовательно, (m8) Длина пути смешения определяется эмпирически. Успех предложенной Прандтлем модели объясняется тем, что для многих простых типов течений со сдвигом lm может быть выражена относительно несложными формулами. При рассмотрении течения в пограничном слое полагают lm = ky, (m9) где k – универсальный коэффициент пропорциональности, не зависящий от числа Рейнольдса: k≈0.39. Это объяснятся тем, что пульсации больше там, где выше скорость. По мере приближения к стенке скорость стремится к нулю; следовательно пульсации уменьшаются. Поэтому путь перемешивания пропорционален расстоянию до стенки. Для свободных слоёв со сдвигом можно в направлении в поперёк слоя полагать константой, пропорциональной толщине слоя. Коэффициент пропорциональности, то есть эмпирическая константа, зависит от типа течения.
![В дополнение к модели пути смешения Прандтль предложил (1942) простую модель вихревой вязкости для свободных сдвиговых течений (модель Прандтля-Райхарда или вторая модель Прандтля): νt = χ·[Umax – Umin]·δ(x) , (m10) где Umax и Umin – максимальная и минимальная величины скорости в слое; δ – полуширин В дополнение к модели пути смешения Прандтль предложил (1942) простую модель вихревой вязкости для свободных сдвиговых течений (модель Прандтля-Райхарда или вторая модель Прандтля): νt = χ·[Umax – Umin]·δ(x) , (m10) где Umax и Umin – максимальная и минимальная величины скорости в слое; δ – полуширин](https://prezentacii.org/upload/cloud/19/05/147596/images/thumbs/screen148.jpg)
Слайд 148В дополнение к модели пути смешения Прандтль предложил (1942) простую модель вихревой вязкости для свободных сдвиговых течений (модель Прандтля-Райхарда или вторая модель Прандтля): νt = χ·[Umax – Umin]·δ(x) , (m10) где Umax и Umin – максимальная и минимальная величины скорости в слое; δ – полуширина слоя смешения; χ – эмпирический безразмерный параметр, постоянный по толщине слоя; x – расстояние, измеренное вниз по течению (в направлении течения). Выражение (m10) получено Райхардом экспериментально для струйных потоков. Для свободных струй, истекающих в затопленное пространство, Umax=Um – скорости на оси симметрии. Umin=0 .
Слайд 149Модель Прандтля является незамкнутой, поскольку длина пути смешения не определена. Несколько позже (около 1940) Карман сделал попытку замкнуть модель Прандтля воспользовавшись второй производной скорости. Из анализа размерности следует (m11) что приводит к (m12) Однако эта гипотеза оказалась менее удачной, чем модель Прандтля.
Слайд 150Значение гипотезы Прандтля для всей теории турбулентных течений 1. Все алгебраические модели построены на основе модели Прандтля. 2. Огромное влияние на дифференциальные модели с одним и двумя уравнениями. Линейный масштаб турбулентности входит практически во все модели.
Слайд 151Пристенные версии алгебраических моделей турбулентности Пристенные версии алгебраических моделей турбулентности в первую очередь настроены на расчёт пограничных слоев. В этой связи, прежде всего, необходимо вспомнить о двуслойной структуре турбулентного пограничного слоя. Важно, что внутренняя и внешняя область пограничного слоя существенно различаются (масштабами, автомодельными законами и т.п.). Это привело к тому, что подавляющее большинство алгебраических моделей турбулентности для пограничных слоев имеют двухслойную структуру.
Слайд 152«Сшивка» решений Как правило, сшивка решений во внутренней и внешней областях производится в точке равенства турбулентной вязкости. С формальной точки зрения это не очень хорошо, поскольку в точке сшивки турбулентная вязкость не дифференцируема, а в уравнениях Рейнольдса она стоит под знаком производной. С практической точки зрения это редко играет существенную роль. Тем не менее, иногда используются гладкие сопряжения (например - ТаnН).

Слайд 153Дополнительные сложности, возникающие при расчёте пограничных слоев При расчёте пристенных течений зачастую возникают некоторые дополнительные сложности. Как правило, они обусловлены наличием дополнительных факторов так или иначе меняющих как профиль скорости в пограничном слое, так и непосредственно характеристики турбулентности. Приведём примеры названных сложностей. 1. Проблема малых чисел Рейнольдса. Рассмотренная модель опирается на обобщение экспериментальных данных по развитым пограничным слоям при значительных числах Рейнольдса. В ситуации, когда число Рейнольдса (по толщине пограничного слоя) не очень велико, турбулентность в пограничном слое не успевает до конца развиться и корреляции, на которых построена данная модель, оказываются не совсем верными. 2. Массообмен через стенку (вдув-отсос) приводит к увеличению (в случае вдува) или уменьшению (в случае отсоса) турбулентных пульсаций. При отсосе толщина пограничного слоя уменьшается (относительно отсутствия массообмена), а при вдуве увеличивается. Кроме того, с точки зрения закона стенки, это приводит к изменению угла наклона логарифмического профиля скорости.

Слайд 1543. Продольный градиент давления не меняет логарифмического закона, но существенно изменяет интенсивность турбулентных пульсаций. Кроме того, при положительном градиенте давления толщина пограничного слоя становится больше, а при отрицательном - меньше, чем в безградиентном пограничном слое. 4. Эффекты сжимаемости, вызванные как большими числами Маха в набегающем потоке, так и сильной неизотермичностью потока, также приводят к изменению логарифмического закона. 5. Шероховатость поверхности может приводить к сдвигу логарифма (изменению константы В). 6. Продольная кривизна поверхности приводит к увеличению (на вогнутой стенке) или уменьшению (на выпуклой стенке) турбулентных пульсаций.

Слайд 155Моделирование пограничных слоев Современные представления о структуре турбулентного пограничного слоя (ТПС) основываются на анализе опытных данных. В ТПС выделяется по меньшей мере пять подобластей: вязкий подслой, переходная или буферная область, область логарифмического профиля скорости, область закона следа и область перемежаемости. Первые три принято объединять в одну внутреннюю область или область закона стенки. Внутренняя область пограничного слоя на плоской пластине занимает примерно 15-20% от толщины всего слоя. Согласно измерениям в ней генерируется до 80% энергии турбулентности, причем первые 5% толщины дают более половины вклада в полное производство турбулентной энергии. Область закона следа и область перемежаемости обычно объединяют во внешнюю область ТПС, которая занимает порядка 80% от толщины всего слоя. Внешняя область ТПС с характерной для нее крупномасштабной турбулентностью обладает «долгой памятью» по Клаузеру. Полное затухание возмущений в этой области происходит на расстоянии, во много раз превышающем линейный масштаб турбулентности. Следовательно, свойства течения во внешней области могут зависеть в большей степени от предыстории потока.

Слайд 156Различные области ТПС отличаются друг от друга разномасштабностью вихревых (когерентных) структур. Цепочка вращающихся в противоположных направлениях продольных вихрей плотно покрывает гладкую стенку. Эти вихри подвержены колебаниям вблизи стенки и в свою очередь порождают низкоскоростные поперечные к потоку жгуты. В эволюции жгутов можно выделить следующие фазы: формирования, подъёма, колебания и разрушения. Последовательность последних трёх фаз принято называть всплеском. Выше низкоскоростных продольных вихрей, но все еще достаточно близко к стенке находится слой, постоянно разрушаемый всплесками. По некоторым данным, всплески дают порядка 70% рейнольдсовых напряжений. Характерным элементом внутренней области являются также мелкомасштабные поперечные вихри большой энергии. Эти вихри частично заполняют буферную область и полностью участок логарифмического профиля скорости. Основными элементами внешней области ТПС являются крупномасштабные поперечные вихревые структуры с характерными размерами порядка толщины слоя и «типичные» вихри с большой энергией в области перемежаемости. Очевидно, что даже схематизированное представление о структуре ТПС являет собой достаточно сложную и не до конца изученную картину взаимодействия структурных элементов.

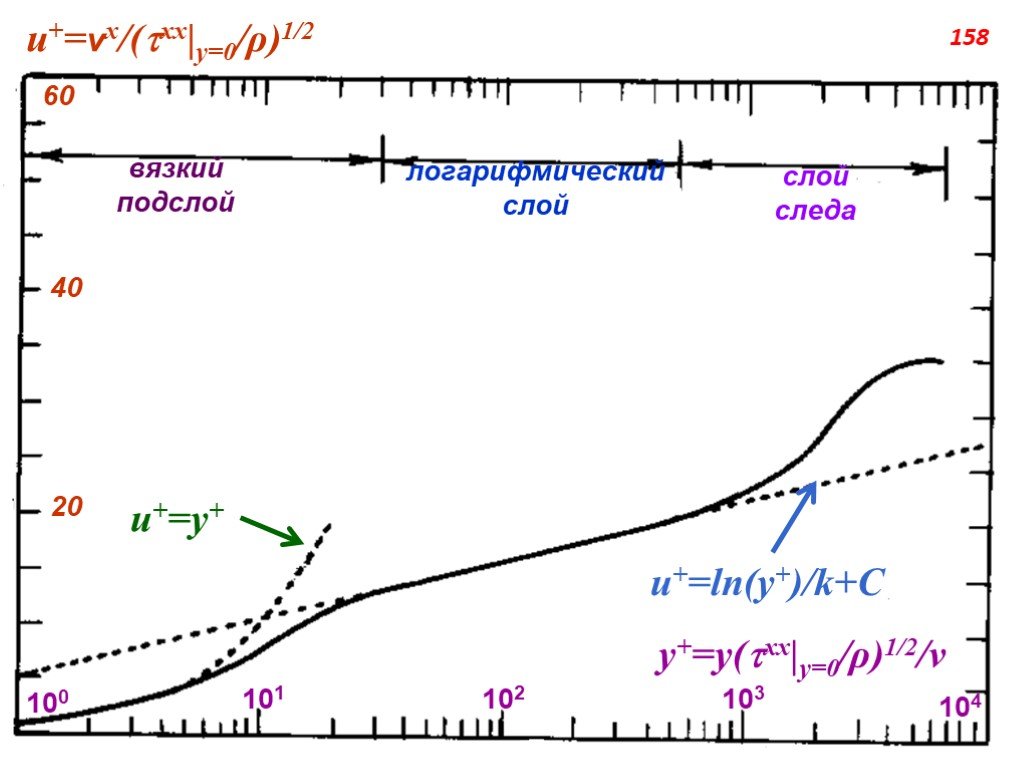
Слайд 157На рисунке показан типичный профиль скорости в ТПС, развивающемся на плоской пластине без градиента давления. Величина у+ выражает обезразмеренное расстояние от стенки. Показаны три участка разбиения профиля: вязкий подслой, логарифмический слой и слой следа. Логарифмический слой определяется как близкая к стенке часть ТПС, где напряжения, обусловленные молекулярной вязкостью, пренебрежимо малы по сравнению с рейнольдсовыми напряжениями, а также незначительны инерционные, конвективные члены. Эта область пролегает между у+=30 и у=0.1δ, где δ – толщина ТПС, а у+ на верхней границе зависит от числа Рейнольдса. Интересно отметить, что закон стенки имеет место в логарифмическом слое. Вязкий подслой располагается между стенкой и логарифмическим слоем. Вблизи стенки скорость изменяется приблизительно линейно с у+ и постепенно переходит к закону стенки при больших у+ . Область следа пролегает между логарифмическим слоем и кромкой ТПС. Скорость асимптотически стремится к закону стенки при у/δ→0 и значительно отличается от него при приближении к внешнему потоку.

Слайд 158вязкий подслой
логарифмический слой
слой следа u+=y+ u+=ln(y+)/k+C 20 40 60 100 101 102 103 104 u+=vx/(xx|y=0/ρ)1/2 y+=y(xx|y=0/ρ)1/2/ν
Слайд 159Область применимости алгебраических моделей В настоящее время алгебраические модели практически уступили свое место дифференциальным. Однако в течениях, для которых разработаны алгебраические модели их применение, безусловно, является оправданным. Но даже в таких ситуациях реализация и использование алгебраических моделей в современных кодах может быть довольно непростой задачей. Кроме того, эти модели могут быть использованы в пристенной области при использовании гибридных методов и при разработке пристенных функций.
Слайд 160
Слайд 161
Слайд 162
Слайд 163
Слайд 164
Слайд 165
Слайд 166
Слайд 167
Слайд 168
Слайд 169
Слайд 170
Слайд 171
Слайд 172
Слайд 173
Слайд 174
Слайд 175
Слайд 176
Слайд 177Огромный опыт, накопленный при эксплуатации полуэмпирических моделей турбулентности, привёл к ясному осознанию того, что надежды на создание универсальной модели турбулентности пригодной для расчёта всех или, по крайней мере, большинства турбулентных течений, казавшиеся вполне реальными ещё в 70–80-х годах прошлого (ХХ) века, едва ли осуществимы. Это, в свою очередь, привело к значительному смещению акцентов в исследованиях, посвященных моделированию турбулентности. Всё больше внимания стало уделяться альтернативным (не использующим RANS) подходам. Однако, в силу исключительной вычислительной трудоёмкости этих подходов, основным инструментом для расчёта сложных турбулентных течений, представляющих практический интерес, по-прежнему остаётся Полуэмпирическая Теория Турбулентности (ПТТ).

Слайд 178В этой области, наряду с традиционными исследованиями, направленными на усовершенствование существующих и разработку новых моделей турбулентности, в последнее время большое внимание уделяется проблеме тестирования и определения границ применимости таких моделей. Эта работа проводится как отдельными исследователями, так и в рамках специальных международных программ, координируемых, в частности, Стэндфордским университетом в США, Комиссией ЕС по развитию научных исследований и Европейским Сообществом по Течениям, Турбулентности и Горению (ERCOFTAC). Целью этих программ является выработка конкретных рекомендаций, позволяющих обоснованно выбрать ту или иную модель турбулентности при решении различных прикладных задач. Значительный вклад в решение данной проблемы внесли три Стэндфордские международные конференции (1968, 1980 и 1990 гг.), получившие неофициальное название «олимпиад моделей турбулентности».

Слайд 179Среди более поздних попыток организации тщательного и всестороннего тестирования моделей турбулентности следует отметить Европейский проект по вычислительной гидродинамике ECARP, в рамках которого проведено сопоставление результатов расчётов достаточно широкого круга турбулентных течений, полученных с использованием самых разнообразных моделей турбулентности несколькими исследовательскими группами с помощью их собственных вычислительных программ. Аналогичные усилия предпринимаются ERCOFTAC, под эгидой которого регулярно проводятся специализированные международные рабочие семинары, посвящённые детальному анализу результаты расчётов, полученных участниками в рамках одних и тех же моделей турбулентности для так называемых "тестовых течений", то есть специально отобранных экспериментов, содержащих, по мнению организаторов, наиболее надёжные и полные данные по тем или иным турбулентным течениям.

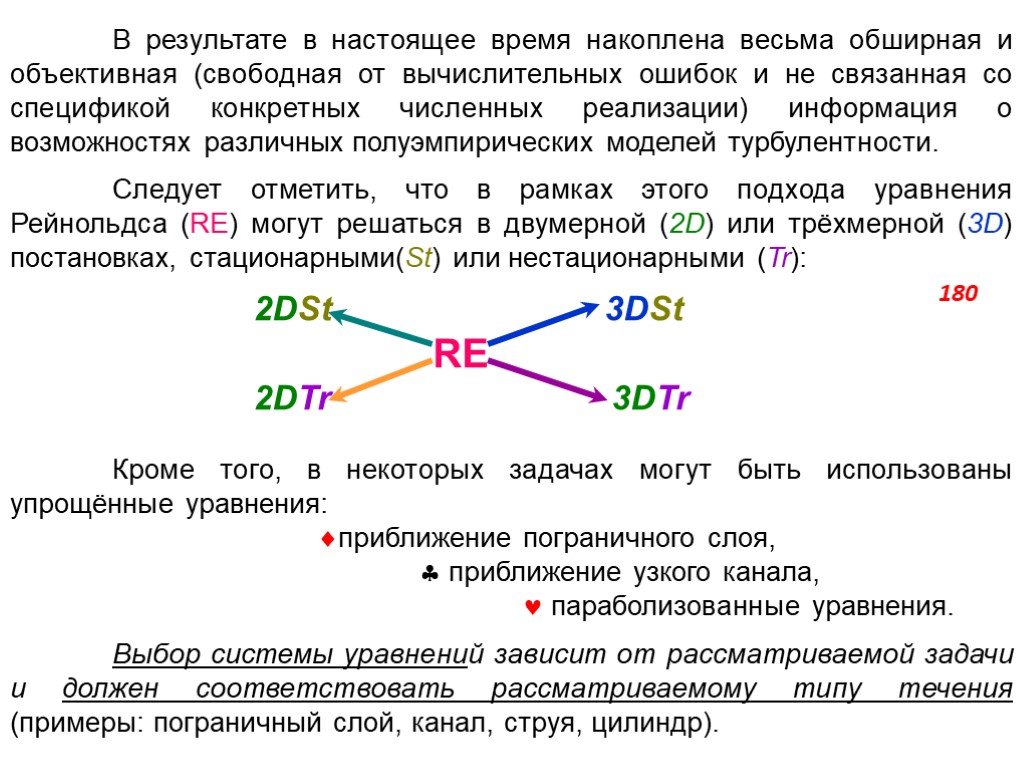
Слайд 180В результате в настоящее время накоплена весьма обширная и объективная (свободная от вычислительных ошибок и не связанная со спецификой конкретных численных реализации) информация о возможностях различных полуэмпирических моделей турбулентности. Следует отметить, что в рамках этого подхода уравнения Рейнольдса (RE) могут решаться в двумерной (2D) или трёхмерной (3D) постановках, стационарными(St) или нестационарными (Tr): 2DSt 3DSt RE 2DTr 3DTr Кроме того, в некоторых задачах могут быть использованы упрощённые уравнения: приближение пограничного слоя, приближение узкого канала, параболизованные уравнения. Выбор системы уравнений зависит от рассматриваемой задачи и должен соответствовать рассматриваемому типу течения (примеры: пограничный слой, канал, струя, цилиндр).

Слайд 181В частности, иногда изначально двумерные задачи решаются в трёхмерной нестационарной постановке (такой подход в западной литературе называется URANS). При этом наиболее крупные когерентные структуры оказываются разрешёнными и характер решения напоминает LES. Однако в силу отсутствия достаточного обоснования этот подход в настоящее время оценивается неоднозначно.
Слайд 182
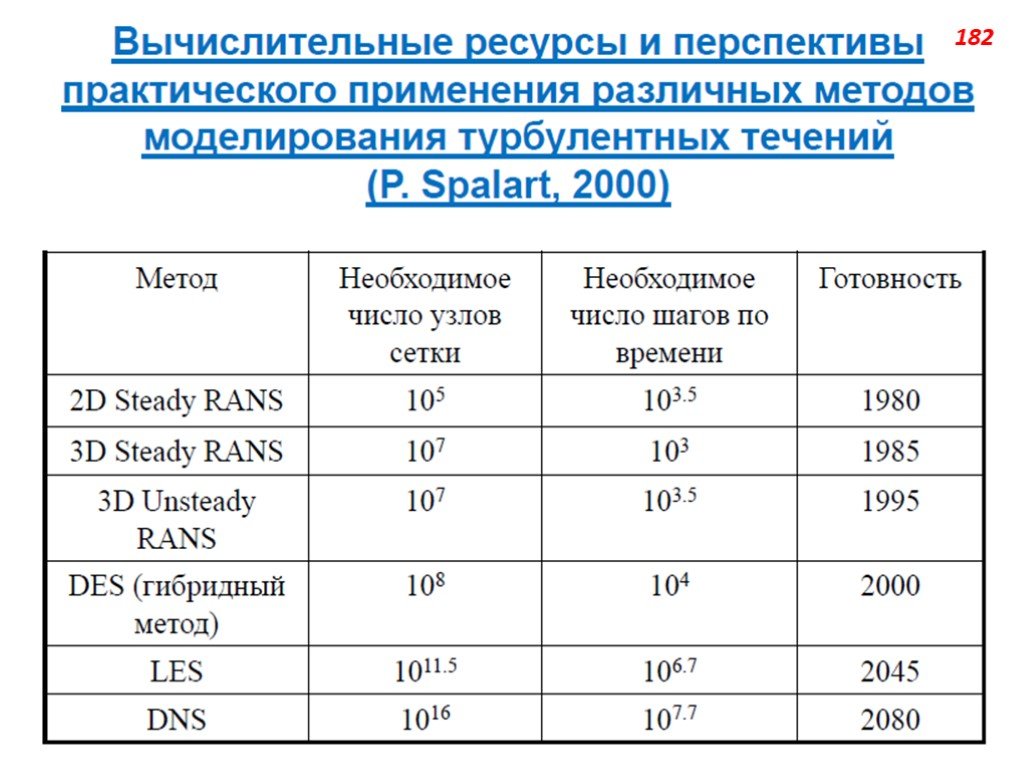
Слайд 183Из таблицы видно, что в ближайшие годы основными подходами к решению сложных прикладных задач будет классический подход, основанный на двумерных и трёхмерных уравнениях Рейнольдса (RANS URANS), или гибридные подходы, включающие его как составную часть. Таким образом, по крайней мере в течение ближайших 40-50 лет, человечество обречено использовать те или иные модели турбулентности.

Слайд 184Вопросы, выносимые на зачёт 1. Конвекция: естественная и вынужденная. Определить, основные различия. Конвективный теплообмен, типы. 2. Конвективная теплоотдача. Коэффициент теплоотдачи (определение, размерность в СИ, типы). Основные факторы, влияющие на величину коэффициента теплоотдачи. Общий вид функциональных зависимостей для числа Нуссельта при различных видах конвекции (сходящие в соотношения величины пояснить). 3. Реологическое соотношение. Ньютоновская жидкость. Идеальная жидкость. Коэффициент (динамически и кинематический) вязкости (определения, размерность). 4. Критериальные числа Рейнольдса, Грасгоффа, Прандтля, Пекле, Нуссельта, Маха. 5. Ламинарное и турбулентное течение. Критическое число Рейнольдса. Каскадный перенос энергии. Колмогоровский масштаб. 6. Усреднение по Рейнольдсу. Общие принципы. Классификация моделей турбулентности.
Слайд 185ДЗЯКУЙ ЗА ЎВАГУ THANK FOR YOUR ATTENTION
СПАСИБО ЗА ВНИМАНИЕ























































































































































































































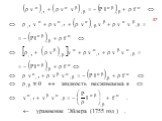













































































![В дополнение к модели пути смешения Прандтль предложил (1942) простую модель вихревой вязкости для свободных сдвиговых течений (модель Прандтля-Райхарда или вторая модель Прандтля): νt = χ·[Umax – Umin]·δ(x) , (m10) где Umax и Umin – максимальная и минимальная величины скорости в слое; δ – полуширин В дополнение к модели пути смешения Прандтль предложил (1942) простую модель вихревой вязкости для свободных сдвиговых течений (модель Прандтля-Райхарда или вторая модель Прандтля): νt = χ·[Umax – Umin]·δ(x) , (m10) где Umax и Umin – максимальная и минимальная величины скорости в слое; δ – полуширин](https://prezentacii.org/upload/cloud/19/05/147596/images/thumbs/screen148.jpg)


































































