Конспект урока «Циркуль» по геометрии
Конспект урока на тему «Циркуль»
С циркулем мы знакомимся в школе. Семейство современных циркулей столь разнообразно, что во многих из них и не признаешь циркуль с первого взгляда.
Циркуль - один из первых инструментов, с которым знакомятся школьники, и одно из древнейших изобретений человека. Но много ли мы знаем об истории циркуля? Как он изменялся и в каком качестве использовался? И всегда ли он выглядел так, как мы привыкли?
Оценить древность использования любого инструмента можно по археологическим находкам - по тем артефактам, которые не могли быть созданы без помощи этого инструмента. Многие древнейшие сооружения времён неолита имеют круглую форму. Круг - один из первых мистических символов человечества, подобный солнцу; он присутствует на многих сакральных изображениях и в символике всех народов мира. На сооружениях практически всех древних цивилизаций были обнаружены следы использования циркуля.

 Время изобретения циркуля неизвестно. Сам принцип описывания окружности с помощью двух равноотстоящих меток (предметов) возник еще во времена каменного века. Окружности можно было описывать и с помощью надломанной или согнутой ветки, и с помощью натянутой гибкой лианы или травинки, и с помощью палки с двумя сучками. Круги могли быть размечены и группой взявшихся за руки людей... А самый простой «циркуль» - это расставленные пальцы человеческой руки, которые применялись и в рисовании дуг, и в измерениях. Главный принцип - постоянное расстояние между двумя точками инструмента - мог быть реализован по-разному. И нарисовать окружность можно различными по внешнему виду инструментами.
Время изобретения циркуля неизвестно. Сам принцип описывания окружности с помощью двух равноотстоящих меток (предметов) возник еще во времена каменного века. Окружности можно было описывать и с помощью надломанной или согнутой ветки, и с помощью натянутой гибкой лианы или травинки, и с помощью палки с двумя сучками. Круги могли быть размечены и группой взявшихся за руки людей... А самый простой «циркуль» - это расставленные пальцы человеческой руки, которые применялись и в рисовании дуг, и в измерениях. Главный принцип - постоянное расстояние между двумя точками инструмента - мог быть реализован по-разному. И нарисовать окружность можно различными по внешнему виду инструментами.
Известно, что в Древней Греции математики уже в VI-V веках до н.э. пользовались циркулями. Какими они были, эти древние инструменты? Скорее всего, в научных исследованиях использовались небольшие инструменты с двумя ножками.
Возможно, одно из древнейших изображений такого циркуля, известное историкам, найдено в Китае. Мифические прародители китайцев Фу-Си и Нюй-Ва держат в руках геометрические инструменты: угольник и циркуль. Видимо, циркуль здесь использован в виде символа знания. Умение применять геометрические инструменты высоко ценилось в тех цивилизациях древности, где математические вычисления были сложны из-за неудобной системы нумерации - будь то иероглифическая запись чисел, или, например, римская нумерация - и «геометрические» вычисления, т.е. результат построений циркулем и линейкой, часто быстрее приводил к результату.
Со времени возникновения геометрических методов древности циркуль является символом знания и тяги к образованию. Например, после изобретения книгопечатания издавались многочисленные «символариумы» - занимательные книжки с картинками; все картинки снабжались интересной и поучительной, чаще всего рифмованной, подписью. И циркуль здесь частый гость - как символ знания, мудрости и стремления к учебе.
Но, кроме изображений циркуля, хотелось бы увидеть его и как исторический артефакт. И здесь на помощь приходит археология.
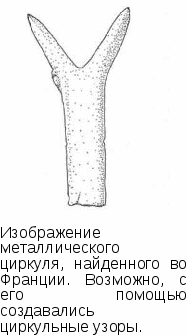 Самый древний из найденных циркулей, датированный I веком н.э., был обнаружен археологами во Франции. Он представляет собой металлическую рогульку, с помощью которой, возможно, процарапывались или размечались небольшие окружности.
Самый древний из найденных циркулей, датированный I веком н.э., был обнаружен археологами во Франции. Он представляет собой металлическую рогульку, с помощью которой, возможно, процарапывались или размечались небольшие окружности.
Подобные найденному во Франции циркулю инструменты широко использовались и во многих других регионах мира для создания так называемых «циркульных» орнаментов на изделиях из дерева, кости, рога и др.
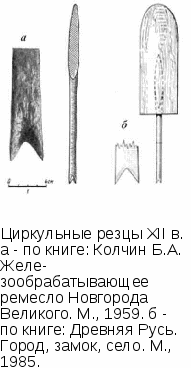 На раскопках в Великом Новгороде были обнаружены металлические циркули-резцы для нанесения циркульных (состоящих из окружностей и дуг) узоров на дерево или кость. Они похожи на древний циркуль, найденный во Франции.
На раскопках в Великом Новгороде были обнаружены металлические циркули-резцы для нанесения циркульных (состоящих из окружностей и дуг) узоров на дерево или кость. Они похожи на древний циркуль, найденный во Франции.
Циркульные узоры были распространены во всех древних цивилизациях. На территории России в самых разных районах обнаружены предметы с такими узорами.
 Но надо сказать, что гораздо более древние изображения окружностей (циркульные узоры) имеются на изделиях протогеометрической керамики, т.е. на древних глиняных сосудах, украшенных простейшими геометрическими орнаментами, в том числе и наборами концентрических окружностей. Такие узоры были обнаружены археологами практически всех регионов мира. Как наиболее изученная, протогеометрическая керамика Средиземноморья (и, в частности, Греции) имеет наибольшую известность. Следует отметить, что не на всех античных керамических сосудах с циркульными узорами эти узоры правильны - видимо, инструменты для нанесения концентрических окружностей на бока сосудов были дороги и не всегда имелись в распоряжении древних мастеров. Но в тех случаях, когда окружности правильные, практически всегда можно заметить в их центре отметку от острия рисующего инструмента - циркуля.
Но надо сказать, что гораздо более древние изображения окружностей (циркульные узоры) имеются на изделиях протогеометрической керамики, т.е. на древних глиняных сосудах, украшенных простейшими геометрическими орнаментами, в том числе и наборами концентрических окружностей. Такие узоры были обнаружены археологами практически всех регионов мира. Как наиболее изученная, протогеометрическая керамика Средиземноморья (и, в частности, Греции) имеет наибольшую известность. Следует отметить, что не на всех античных керамических сосудах с циркульными узорами эти узоры правильны - видимо, инструменты для нанесения концентрических окружностей на бока сосудов были дороги и не всегда имелись в распоряжении древних мастеров. Но в тех случаях, когда окружности правильные, практически всегда можно заметить в их центре отметку от острия рисующего инструмента - циркуля.
Интересно здесь отметить, что в Греции существовала легенда о том, что Талоc (или же Пердикс, ученик и племянник Дедала) «сделал железную копию челюсти рыбы и, таким образом, изобрёл пилу... изобрёл гончарный круг, а также приспособление для черчения окружностей...».
Надо сказать, что греки приписывали своим согражданам или мифическим героям многие открытия, и причин этому было несколько. Во-первых, молодая государственность в окружении древних египетской и шумерской цивилизаций стремилась самоутвердиться. А, во-вторых, у древнего человека не укладывалось в голове, что одно и то же приспособление могло быть независимо изобретено разными людьми в разных местах и в разное время. Кроме того, в Древней Греции, в отличие от других древних цивилизаций, очень рано возникло понятие авторства - у значительной части греческих сочинений, изобретений или художественных произведений были известны авторы. И поэтому в эллинистическом мире стремились знать авторов значимых изобретений, а если таковых не было, ими становились мифические или полумифические персонажи.
 Но циркули существовали задолго до возникновения греческих государств. Изобретение металлических циркулей можно отнести ко времени появления у человека первых бронзовых изделий. Дело в том, что изготовление предметов из металла, их ковка предполагают наличие клещей (и эти инструменты как атрибуты ремесленника часто встречаются на древних египетских и греческих изображениях). Но ведь конструкция клещей и циркуля практически одинакова! Кроме того, многочисленные медицинские (хирургические) инструменты, в том числе пинцеты, древние ножницы пружинного и шарнирного вида, которые обнаруживаются археологами в самых разных уголках мира, - всё это тоже близкие «родственники» циркуля.
Но циркули существовали задолго до возникновения греческих государств. Изобретение металлических циркулей можно отнести ко времени появления у человека первых бронзовых изделий. Дело в том, что изготовление предметов из металла, их ковка предполагают наличие клещей (и эти инструменты как атрибуты ремесленника часто встречаются на древних египетских и греческих изображениях). Но ведь конструкция клещей и циркуля практически одинакова! Кроме того, многочисленные медицинские (хирургические) инструменты, в том числе пинцеты, древние ножницы пружинного и шарнирного вида, которые обнаруживаются археологами в самых разных уголках мира, - всё это тоже близкие «родственники» циркуля.
То есть циркуль был известен задолго до начала становления греческой цивилизации. Быть может, Талос (или Пердикс) изобрёл не циркуль, а приспособление для создания циркульных узоров? Возможно, это было приспособление типа штангенциркуля с несколькими рисующими стержнями?
Вернёмся к древнейшему известному циркулю. Надо сказать, что много гораздо более совершенных разнообразных бронзовых инструментов, в том числе и циркулей, было найдено в развалинах Помпеи; следы циркульной разметки заметны на некоторых древнеримских монетах.
Б
ронзовые инструменты, найденные в Помпеях.
Итак, циркуль был известен человеку с древнейших времен. Но всегда ли он был таким - с двумя ножками? Ясно, что принцип действия циркуля - это постоянное расстояние между двумя его точками. И этот принцип можно реализовать по-разному, поэтому исторически циркули были трёх основных видов, и предназначены они были для выполнения трёх основных операций - рисования окружностей и дуг, измерения и разметки.
Все мы привыкли воспринимать циркуль как инструмент с двумя ножками-стержнями, закреплёнными шарнирным соединением. Но истории известны и другие конструкции циркулей. Это верёвочные циркули (два стержня, связанных бечевой), штангенциркули (закреплённые на одной балке параллельные стержни) и всем знакомые кронциркули или циркули с головкой (две ножки-стержня, шар-нирно соединённые головкой). К семейству кронциркулей относятся также «пропорциональные» и «совершенные» циркули.
Самый простой тип циркуля - это верёвочный циркуль, т.е. верёвка с отмеченными на ней (чаще всего узлами) расстояниями или с закреплёнными на концах стержнями. Такие инструменты использовались, например, в Древнем Египте при разметке земельных участков после очередного разлива Нила. Несмотря на свою примитивность, верёвочный циркуль используется и сейчас - там, где надо нарисовать дугу очень большого радиуса (например, при разметке спортивных арен) или там, где использование «жёсткого» циркуля неудобно - их часто можно увидеть в руках садовников и кровельщиков.
Другой вид циркуля - это штангенциркуль, или циркуль, короткие ножки которого могут передвигаться вдоль размеченной планки (штанги) - естественное усовершенствование верёвочного циркуля. Такие циркули применяются в основном при измерении - и достаточно больших объектов, и очень маленьких. С помощью штангенциркуля можно измерять не только наружную толщину предмета, но и внутренний диаметр отверстий, и их глубину. Штангенциркулями пользуются и лесники для измерения стволов деревьев, и ювелиры для оценки размеров обрабатываемых миниатюрных изделий. Штангенциркули существуют достаточно давно: в европейских музеях сохранились деревянные штангенциркули сапожников - такие циркули давали достаточно грубые результаты измерений. Сейчас движущуюся планку металлического штангенциркуля часто оснащают винтом, чтобы иметь возможность фиксировать расстояния более точно. Измерительные штангенциркули оснащаются электронной аппаратурой и могут измерять предметы с потрясающей точностью. Они же используются сейчас, например, и при вырезании круглых отверстий, поскольку являются родственником инструментов для высверливания или вырезания больших отверстий.
Но лучше всего нам знаком циркуль с двумя шарнирно соединёнными ножками, или кронциркуль (циркуль с головкой).
Было изобретено огромное количество модификаций кронциркулей - от миниатюрных «балеринок» для вычерчивания очень маленьких окружностей до больших землемерных циркулей. Существуют циркули для черчения и для измерения. Ювелиры используют миниатюрные кронциркули с заточенными металлическими ножками - с их помощью тончайшими царапинами размечаются контуры рисунков на изделия.

Для измерений применяются циркули с прямыми и изогнутыми ножками - такая форма удобна для измерения внутренних размеров через небольшое отверстие или для измерения толщины широких пластин в разных их местах (эту задачу решают, например, музыкальные мастера, выверяя толщины деки инструмента).
 Для рисования окружностей большого радиуса были придуманы циркули, у которых одна удлинённая и изогнутая ножка позволяла рисовать такие окружности относительно небольшим инструментом - «скрещивание» кронциркуля и штангенциркуля дает компактный инструмент для вычерчивания больших окружностей. Добавлялись дополнительные ножки и фиксаторы-шкалы для определения размеров. Иногда при работе циркули располагали горизонтально, а на их ножках крепились подставки-бегунки, которые также участвовали в измерениях или разметке чертежа. Без циркуля не мыслилась деятельность специалистов многих профессий. Например, у артиллеристов специальный военный циркуль, снабжённый отвесом и различными шкалами, позволял произвести наиболее точное прицеливание.
Для рисования окружностей большого радиуса были придуманы циркули, у которых одна удлинённая и изогнутая ножка позволяла рисовать такие окружности относительно небольшим инструментом - «скрещивание» кронциркуля и штангенциркуля дает компактный инструмент для вычерчивания больших окружностей. Добавлялись дополнительные ножки и фиксаторы-шкалы для определения размеров. Иногда при работе циркули располагали горизонтально, а на их ножках крепились подставки-бегунки, которые также участвовали в измерениях или разметке чертежа. Без циркуля не мыслилась деятельность специалистов многих профессий. Например, у артиллеристов специальный военный циркуль, снабжённый отвесом и различными шкалами, позволял произвести наиболее точное прицеливание.
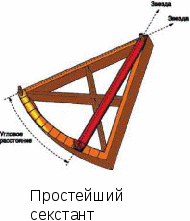
Разновидностью циркуля являлось и большинство навигационных инструментов; всем известный секстант - это тоже кронциркуль со специфическими шкалами.
 С древнейших времён существовали и пропорциональные циркули. Они предназначались для пропорционального изменения в заранее заданном отношении размеров измеряемого или проектируемого объекта. Один из таких циркулей был найден в Помпейских развалинах. Это был циркуль золотого сечения: раствор разных концов соединённых шарниром в средней части ножек находился в постоянном отношении (в отношении золотого сечения). Были придуманы циркули и с подвижным относительно концов ножек положением шарнира. Такой циркуль позволял легко в произвольной заданной пропорции увеличивать или уменьшать размеры чертежа или измеряемого объекта.
С древнейших времён существовали и пропорциональные циркули. Они предназначались для пропорционального изменения в заранее заданном отношении размеров измеряемого или проектируемого объекта. Один из таких циркулей был найден в Помпейских развалинах. Это был циркуль золотого сечения: раствор разных концов соединённых шарниром в средней части ножек находился в постоянном отношении (в отношении золотого сечения). Были придуманы циркули и с подвижным относительно концов ножек положением шарнира. Такой циркуль позволял легко в произвольной заданной пропорции увеличивать или уменьшать размеры чертежа или измеряемого объекта.

Снабжение циркулей разнообразными и позволяющими решать многочисленные задачи шкалами превратило циркуль в измерительно-вычислительный инструмент, или «пропорциональный циркуль» (под этим названием понимались два вида кронциркулей - уже упомянутый циркуль-делитель и циркуль с широкими ножками-шкалами).
Пропорциональный циркуль с широкими плоскими пластинами-ножками часто располагался горизонтально на чертеже или на местности, и при больших размерах инструмента ему была необходима подставка. Иногда такими подставками были бегунки-указатели с ножками на нижней стороне. Подобно стеклышку на не совсем ещё позабытой логарифмической линейке, такие бегунки позволяли более точно снимать показания со шкал пропорционального циркуля.

Но был в истории циркуля и ещё один загадочный персонаж. Это - одна из модификаций кронциркуля - «совершенный» или эллиптический циркуль, созданный в античности для вычерчивания гипербол, парабол и эллипсов, и реконструированный арабоязычными учёными в X веке.
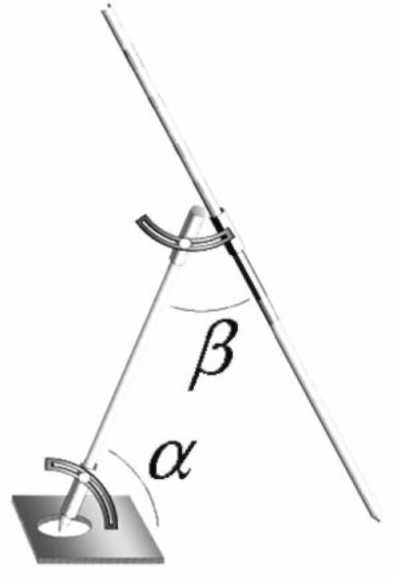
Реконструкция совершенного циркуля по тексту учёного X в. Ас-Сиджизи.
В зависимости от соотношения углов а ив конец длинного стержня описывает на плоскости эллипс, гиперболу или параболу. Короткая фиксированная ножка циркуля здесь представляет ось конуса, а длинная, свободно двигающаяся в трубке - его образующую. Поэтому если а = в, то будет нарисована гипербола, если а, то получится парабола, а если а > в - эллипс.
В чём причина появления такого необычного инструмента? И зачем рисовать эти кривые столь необычным способом?
Появление инструментов для рисования конических сечений (эллипса, гиперболы и параболы) относится ко временам древнегреческой математики. Дело в том, что, греческие учёные решали большинство возникавших в практике задач с помощью циркуля и линейки. Причиной этому была не какая-то сверх-идея или стремление к некой абстрактной науке - нет, причина была та же самая, что и у китайцев, которые обожествили циркуль и угольник, дав его в руки своим мифическим прародителям. По этой же причине в Древней Индии алгебраические задачи решали геометрически, но вместо жёсткого циркуля и линейки использовали бечеву («Шульба-сутра», или «Правила верёвки», VI век до н.э.). И египтяне, как известно, использовали натянутые верёвки при разметке участков в плодородной долине Нила...
У всех древних цивилизаций было одно общее несчастье - крайне неудобная для вычислений система нумерации. Сначала у всех народов это была иероглифическая система (когда каждому числу соответствовал специальный значок или группа значков), затем эти системы несколько совершенствовались. Но только после повсеместного распространения привычной нам позиционной десятичной «арабской» системы нумерации быстрое вычисление произведений, дробей и даже корней (квадратных и кубических, наиболее часто встречающихся в практике) стало возможным после небольшой арифметической  подготовки. А пока такой удобной нумерации не было, древние землемеры, зодчие и конструкторы выходили из положения, решая арифметические и алгебраические задачи геометрическими методами, что часто было гораздо проще и быстрее утомительных и сложных вычислений. Например, арифметически непростая операция вычисления квадратного корня сводится всего лишь к вычерчиванию полуокружности и восставлению перпендикуляра.
подготовки. А пока такой удобной нумерации не было, древние землемеры, зодчие и конструкторы выходили из положения, решая арифметические и алгебраические задачи геометрическими методами, что часто было гораздо проще и быстрее утомительных и сложных вычислений. Например, арифметически непростая операция вычисления квадратного корня сводится всего лишь к вычерчиванию полуокружности и восставлению перпендикуляра.
Древние конструкторы и математики научились решать геометрически достаточно широкий круг задач; сейчас это искусство называется «геометрической алгеброй» древних. Они знали, как строить многие геометрические объекты с помощью циркуля и линейки; умение выполнять такие построения и сейчас свидетельствует о хорошем развитии интеллекта. Навык решения вычислительных и алгебраических задач с помощью циркуля и линейки высоко ценился, и неслучайно поэтому циркуль часто связывали с божествами - например, в Древнем Риме циркуль являлся атрибутом музы астрономии Урании, а в Средние века в Европе циркуль зачастую был в руках Бога-Творца или Спасителя.
 Но античные конструкторы столкнулись с невозможностью решить с помощью циркуля и линейки задачу об извлечении кубического корня, а ведь такая задача часто возникала при необходимости пропорционально изменить размеры некоего объекта, например сосуда или осадного орудия таким образом, чтобы эти размеры соответствовали наперед заданным характеристикам объёма или веса. О том, что такая задача была очень важна для практики, говорят многочисленные легенды о появлении одного из частных её случаев - задачи «об удвоении куба». Эта задача, как и другая знаменитая неразрешимая задача древности о трисекции угла, является задачей третьего порядка, т.е. сводится к решению кубического уравнения. Сейчас известно, что такие задачи невозможно решить с помощью циркуля и линейки.
Но античные конструкторы столкнулись с невозможностью решить с помощью циркуля и линейки задачу об извлечении кубического корня, а ведь такая задача часто возникала при необходимости пропорционально изменить размеры некоего объекта, например сосуда или осадного орудия таким образом, чтобы эти размеры соответствовали наперед заданным характеристикам объёма или веса. О том, что такая задача была очень важна для практики, говорят многочисленные легенды о появлении одного из частных её случаев - задачи «об удвоении куба». Эта задача, как и другая знаменитая неразрешимая задача древности о трисекции угла, является задачей третьего порядка, т.е. сводится к решению кубического уравнения. Сейчас известно, что такие задачи невозможно решить с помощью циркуля и линейки.
Уже в V веке до н.э. математик Гиппократ Хиосский определил, что для решения задачи об определении кубического корня необходимо найти два средних пропорциональных.
Немного позднее, в IV веке до н.э. Менехм, ученик Евдокса Книдского и член Афинской Академии Платона, обнаружил, что для решения задачи «об удвоении куба» по предложенной Гиппократом схеме достаточно найти пересечения кривых, уравнения которых мы сейчас бы записали как ау = х2 и bx = y2, т.е. надо найти пересечение двух парабол или параболы и гиперболы.
Но главное достижение Менехма - он обнаружил, что эти кривые являются сечениями конуса (Менехм рассматривал только прямоугольные конусы, но позднее выяснилось, что годятся конусы с любым углом при вершине).
Видимо, уже тогда были сделаны первые попытки вычерчивания эллипса, гиперболы и параболы на основе их происхождения как конических сечений. А примерно через 100 лет после открытия Менехма другой греческий математик Аполлоний из Перги написал огромный труд о конических сечениях, в котором определял «симптомы» или характерные свойства этих кривых, которые позволяли изобретать приборы для их удобного и точного вычерчивания по заранее заданным характеристикам.
 Но вернёмся к «совершенному циркулю». Его несложно смастерить из двух «козьих ножек» - и убедиться, что им очень неудобно пользоваться. Даже исхитрившись начертить с его помощью более или менее качественную кривую, очень трудно определить, где её оси и фокусы - а их надо знать для того, чтобы использовать при решении задачи «об удвоении куба», или, в общем виде, задачи третьего порядка.
Но вернёмся к «совершенному циркулю». Его несложно смастерить из двух «козьих ножек» - и убедиться, что им очень неудобно пользоваться. Даже исхитрившись начертить с его помощью более или менее качественную кривую, очень трудно определить, где её оси и фокусы - а их надо знать для того, чтобы использовать при решении задачи «об удвоении куба», или, в общем виде, задачи третьего порядка.
Кстати говоря, математики мусульманского Востока, которые реконструировали и исследовали совершенный циркуль, уже не нуждались в графическом решении задач - ведь они владели заимствованной у индийцев десятичной позиционной нумерацией (той самой «арабской», которая позднее пришла в Европу), и при решении конкретных вычислительных задач доводили решение до достаточно точного результата. А вопросы использования геометрических методов при решении алгебраических задач они заимствовали из греческих математических сочинений. И, преклоняясь перед великой учёностью античных математиков, они бережно сохраняли и творчески дополняли сочинения Евклида, Архимеда, Диофанта, Аполлония, Герона и др. В этом ряду стоит и сочинение ас-Сиджизи о «совершенном циркуле» - не имея практической пользы, оно было образцом исследования теоретического знания древних.
А как же решали задачу об удвоении куба греки? Изучив «симптомы» конических сечений, они научились достаточно точно вычерчивать конические сечения по заданным характеристикам при помощи специальным образом расположенных бечёвок и шарнирных механизмов, а также изобрели новые кривые для решения задач третьего порядка (конхоиду, циссоиду, спираль и пр.), которые можно было строить механическими приспособлениями. Кроме того, они создали чрезвычайно остроумные инструменты, извлекающие кубические корни без вычерчивания кривых.
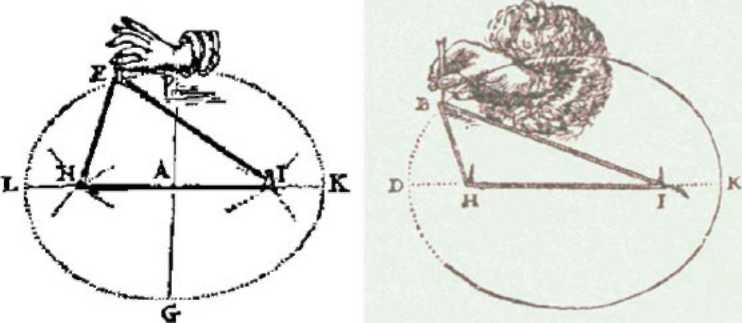 Построение эллипса на основе его фокального свойства.
Построение эллипса на основе его фокального свойства.
«Метод садовника» вычерчивания эллипса использует открытое в древности свойство эллипса: сумма расстояний от его точек до двух фиксированных - фокусов - постоянна. Подобные «верёвочные» приспособления были изобретены и для вычерчивания гипербол и парабол. При таком построении известны оси и фокусы конического сечения, которые необходимо знать для графического решения задачи «об удвоении куба».
Итак, циркуль в течение многих столетий был основным инструментом математика, механика, инженера, ремесленника. В Средние века и в эпоху Возрождения искусство владения циркулем высоко ценилось в среде художников, ювелиров, архитекторов и квалифицированных ремесленников. Циркуль появляется на гербах цеховых гильдий каменщиков, плотников и пр. в различных городах Европы. Умение быстро разметить с помощью циркуля размеры и контуры создаваемого объекта было необходимым условием признания мастерства - и во многих городах проводятся соревнования по решению практических задач с помощью циркуля и линейки. Циркуль квалифицированного ремесленника, снабжённый дополнительными приспособлениями, украшенный узорами и аллегорическими изображениями, был дорогим и точным инструментом. Размеры циркулей менялись от миниатюрного циркуля ювелира до полуметровых и более циркулей каменщиков.
Но так было лишь до тех пор, пока не стала общеупотребительной позиционная, удобная в вычислениях система нумерации. Циркуль как вычислительное средство потерял своё значение, и основным его применением стали разметка (построение чертежей) и измерение. Впрочем, в некоторых областях человеческой деятельности умение управляться с циркулем важно и по сей день (например, при создании музыкальных инструментов или в ювелирном искусстве). Важную роль стали играть пропорциональные циркули как средство облегчения вычислений при решении практических задач - но это, скорее, были не геометрические, а номографические методы (т.е. методы, основанные на использовании предварительно построенных чертежей, специфических для каждого типа задач).
К началу XVI века античные методы решения задач с помощью циркуля и линейки и математика, основанная на геометрии, стали восприниматься учёными уже как исключительно теоретические построения древнегреческих мыслителей, стремившихся к отвлечённому знанию (немалую роль в формировании такого отношения к греческой науке сыграла и наука мусульманских стран). При этом циркуль активно применялся в самых разных областях деятельности человека - в первую очередь, это архитектура и строительство, затем - ювелирное дело и живопись, типографское дело и пр. Циркуль здесь - необходимый инструмент ремесленника и художника. О своей работе по разметке рисунка на сложных ювелирных изделиях рассказывает, например, Бенвенуто Челлини (1500-1571) в своих мемуарах. А известный художник и математик Альбрехт Дюрер (1471-1528) создал специальное учебное пособие для ремесленников, в котором привёл не только точные способы построения правильных геометрических фигур с помощью циркуля и линейки, но и приближённые методы для тех случаев, когда точное построение невозможно (например, построение правильного девятиугольника). Впрочем, эти приближённые методы построения правильных фигур настолько искусны, что отличие построенной фигуры от правильной невооружённым глазом заметить невозможно.
А как обстояло дело в России?
 Согласно исследованиям наших археологов и историков, основным измерительным инструментом при возведении зданий на Древней Руси являлись специально размеченные измерительные шесты - мерила. Но у наших предков уже в IX веке имелись и различные металлические инструменты: щипцы, клещи, ножницы и пинцеты. Жители Древней Руси умели делать сложные замки, а для этого надо было уметь производить достаточно точные измерения и переносить размеры с модели на изготавливаемую деталь. По этим данным можно судить о наличии у них циркулей.
Согласно исследованиям наших археологов и историков, основным измерительным инструментом при возведении зданий на Древней Руси являлись специально размеченные измерительные шесты - мерила. Но у наших предков уже в IX веке имелись и различные металлические инструменты: щипцы, клещи, ножницы и пинцеты. Жители Древней Руси умели делать сложные замки, а для этого надо было уметь производить достаточно точные измерения и переносить размеры с модели на изготавливаемую деталь. По этим данным можно судить о наличии у них циркулей.
Наиболее известный материал по истории культуры нашей страны - это художественное наследие, в первую очередь - иконы. Если внимательно присмотреться, то на большинстве русских икон можно увидеть следы процарапанных на основе иконы окружностей - намеченных контуров нимбов изображённых персонажей. Под слоем краски на старинных иконах можно различить и углубления в центрах процарапанных окружностей. Причём эти окружности имеют стандартные размеры.
При изображении массовых сцен и на клеймах, обрамляющих «житийные» иконы, все нимбы имеют одинаковые радиусы (т.е. на одной иконе могут быть изображены нимбы двух-пяти, а иногда и большего количества стандартных размеров); у главных персонажей иногда в изображении нимба использовались концентрические окружности. О том, каким инструментом процарапывались эти контуры на православных иконах, мы можем судить по мозаичному изображению виллы Эвстолия в Курионе (Кипр).
В руке персонажа мы видим штангенциркуль-чертилку размером около 20 см - видимо, именно такие инструменты использовались при вычерчивании больших нимбов, а для малых нимбов могли быть использованы и приспособления, подобные древним новгородским циркулям-царапкам. Впрочем, реставраторы считают, что для отдельных больших нимбов могли быть использованы и верёвочные циркули.
А использовались ли на Руси кронциркули? Как уже говорилось, основным инструментом древнерусского зодчего было мерило - размеченный несколькими шкалами шест, с помощью которого отмечались на возводимом сооружении необходимые размеры. Но для мелких работ такие приспособления не годятся.
Циркуль на Руси был не только инструментом учёного. В XV-XVII веках учёт земельных угодий вёлся в соответствии с правилами «сошного письма» о начислении податей в зависимости от количества и качества земли. С XVI века использовались специальные руководства - рукописные «Книги сошного письма», содержащие также некоторые сведения из геометрии и геодезии. Видимо, уже тогда началось использование землемерных циркулей раствором в одну сажень (около 1,5-2 метров); сейчас землемерные циркули обычно имеют раствор 1 или 2 метра.
В древности на Руси циркуль назывался «кружало», а современное его название происходит от немецкого Zirkel или польского Cyrkiel и вошло в русский язык в петровские времена. Заметим, что, в свою очередь, это слово происходит от латинского слова circulus или circus - круг, цирк. А слово «центр» (круга) происходит от греческого Kevxpov - остриё (одной из ножек циркуля).
Можно предположить, что первым европейцем, использовавшим циркуль в сакральных или магических целях, был руководитель своеобразной научно-мистической школы-секты Пифагор. Мы знаем, что первые пифагорейцы опознавали друг друга по некоему геометрическому символу, неизвестному другим. Возможно, это была пентаграмма или пятиугольная звезда, точное построение которой (при помощи циркуля и линейки) непросто.
С развитием связей России с Европой циркуль становится геральдическим символом и в нашей стране. В подражание западным традициям начинают создаваться гербы дворянских родов, и циркуль появляется на них - как на гербах старинных дворянских родов, так и на гербах дослужившихся до дворянства чиновников и офицеров. Причем циркуль с поднятыми вверх ножками символизирует масонство, а прямой угол циркуля - твердость и прямоту обладателя герба.

Российские дворянские гербы.
а. Герб Картмазовых - «гласный» герб: изображена карта и циркуль - атрибуты рисования (мазания] карт. б. Герб Горихвостова, указавшего здесь своё масонство. в. Герб Михеева, заслужившего потомственное дворянство государственной службой.
С
охранились многочисленные образцы местных денег периода первых послереволюционных лет, украшенных в том числе и изображением циркуля.
Позднее циркуль был помещен на герб ГДР
На купюре 50 германских марок выпуска 1989 г. рядом с портретом немецкого архитектора Бальтазара Неймана (1687-1753) помещено изображение пропорционального циркуля - основного инструмента зодчего тех времен. А на памятной монете 2000 г., посвящённой С.В. Ковалевской, циркуль символизирует математику.

Боны (платёжные знаки) Черноморской ж.д.
Из коллекции московского коллекционера-бониста А.В. Ломакина.
Казалось бы, циркуль - скучный и невзрачный инструмент... А сколь богата его история и значительно влияние на развитие нашей цивилизации!
Здесь представлен конспект к уроку на тему «Циркуль», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
