Конспект урока «ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ» по геометрии для 7 класса

Сватковская Елена Александровна,

учитель математики

МБНОУ «Лицей № 3 (искусств)»

г. Тула

ПЛАН-КОНСПЕКТ урока геометрии в 7 классе

по теме «ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ»

Цели урока:

• Содержательная: с помощью практических заданий обеспечить понимание учащимися отличия между определением равенства треугольников по шести парам элементов и по признакам, основанным на сравнении трех пар элементов;

• Деятельностная:

а) формировать у учащихся навыки доказательства теорем с опорой на ранее

введенные понятия и доказанные утверждения;

б) формировать у учащихся умения определять равенство треугольников, опираясь

на формулировку первого признака;

• Развивающая: формировать ключевые компетенции учащихся: информационную (умение анализировать информацию и переводить ее из одной формы в другую), проблемную и коммуникативную.

На данном уроке дети должны:

• Усвоить, что в равенстве треугольников можно убедиться несколькими способами: два из них им уже известны, а третий способ – первый признак равенства треугольников;

• Усвоить алгоритм доказательства первого признака;

• Сделать первые шаги по применению первого признака для доказательства равенства треугольников при решении задач;

• Научиться находить в равных треугольниках соответственные равные элементы.

Содержание учебного материала: первый признак равенства треугольников и простейшие задачи на его применение.

Единица содержания образования: способ доказательства теоремы – мысленное совмещение треугольников; выделение при решении задач на использование первого признака трех пар соответственно равных элементов – двух сторон и угла между ними.

Подготовительный этап.

ШАГ 1 – мотивирование: актуализация опорных знаний и фиксирование затруднения в пробном действии.

1. Вопросы для обсуждения:

   • «Сформулируйте определение треугольника»

   • «Какие фигуры называются равными?»

   • «Как определить, равны ли два треугольника?» ( а)наложить друг на друга – равные полностью совместятся; б) измерить и сравнить 6 пар элементов – в равных треугольниках все 6 элементов (3 стороны и 3 угла) одного треугольника будут соответственно равны элементам другого треугольника);

   • «Как определить равенство треугольников на местности?»

2. Устно решить задачи:

• «Верно ли утверждение: если треугольники равны, то равны и их периметры?»

• «Периметры двух треугольников равны. Равны ли эти треугольники?»

• «При наложении треугольника АВС на треугольник FEK сторона АВ совместилась со стороной FE, а сторона АС со стороной FK. Совместилась ли сторона ВС со стороной EK?»

Учитель: Сегодня вы сами себе поставите оценки за урок, заполняя карточку самооценки.

Самооценка работы на уроке

Д/З (3)

3. Проверка домашнего задания в группах.

Каждой группе из четырех человек выдается конверт с четырьмя моделями треугольников. Три из низ равны треугольникам, начерченным в домашнем задании, и они одного цвета, а четвертый отличается по цвету. Дети сравнивают свои чертежи с моделями.

Учитель: Подсчитываем баллы за домашнее задание – по 1 баллу за верно выполненные задания №89 (а,б,в) (правильно построенные треугольники). Максимум 3 балла.

4. Вопросы для обсуждения:

• «Почему в №89 у всех получились равные треугольники, несмотря на то, что были известны не все шесть элементов?»

• «Сколько элементов было задано для построения треугольников?»

• «Как эти элементы расположены относительно друг друга?»

• «Чем похожи задания в № 89 (а,б,в)?»

• «Можно ли по трем парам равных элементов делать вывод о равенстве треугольников?»

5. Учитель: Ребята, в ваших моделях остался еще один треугольник, который не

совместился ни с одним из начерченных вами. Однако, две его стороны и угол имеют те же размеры, что и треугольник в №89 (б). Что это за треугольник?

Ваня решил поэкспериментировать и построил еще один треугольник, взяв все числа из этой задачи. Но его новый треугольник при наложении явно не совпал с первым – получились два разных треугольника. Ване пришлось задуматься: в этих треугольниках есть две пары равных сторон и пара равных углов.

Так достаточно ли трех пар равных элементов, чтобы сделать вывод о равенстве треугольников?
Ребята, в чем состоит отличие этих двух треугольников? (заданный угол в первом треугольнике находиться между заданными сторонами, а в новом – против одной из заданных сторон).

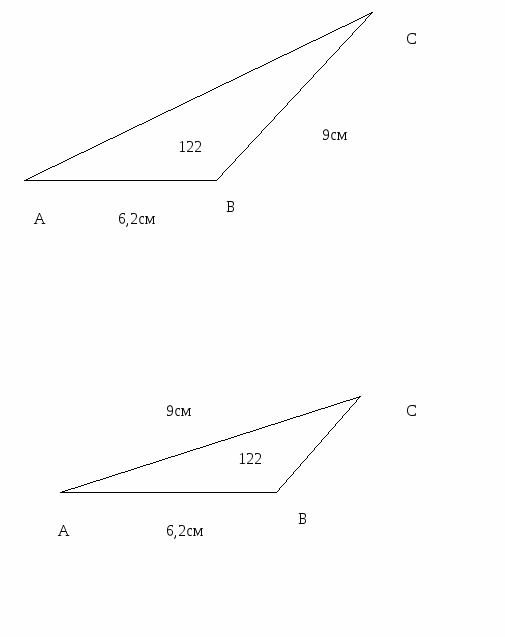
ШАГ 2 – рефлексия изменившихся условий: понимание места и причины затруднения, определение границы между знанием и незнанием.

В результате обсуждения учащиеся приходят к следующим выводам:

• «Наверное, можно говорить о равенстве треугольников только по трем парам элементов, но выбирать их надо не случайно. Есть какая-то закономерность – признак равенства треугольников по трем элементам»;

• «Гипотеза: треугольники равны, если у них соответственно равны две пары сторон и углы, лежащие между этими сторонами».

Учитель: данная гипотеза выражает первый признак равенства треугольников (всего их будет три), который нам предстоит доказать и затем использовать при решении задач. Записываем тему урока: «Первый признак равенства треугольников».

ШАГ 3 – постановка учащимися цели урока как собственной учебной задачи.

Учащиеся ставят следующие цели:

• Узнать признаки, по которым можно судить о равенстве треугольников, не проверяя равенство всех шести пар элементов;

• Доказать теорему: «Треугольники равны, если у них соответственно равны две пары сторон и углы, лежащие между этими сторонами»;

• Учиться находить равные треугольники, используя полученный признак.

ОСНОВНОЙ ЭТАП – ОТКРЫТИЕ НОВЫХ ЗНАНИЙ.

ШАГ 4 – разработка проекта выхода из затруднения.

План действий (проектируется учащимися под руководством учителя):

1. прочитаем внимательно формулировку теоремы, сделаем чертеж и запишем, что дано, а что требуется доказать:

2. будем доказывать, что треугольники равны, мысленно накладывая один на другой.

ШАГ 5 – реализация готового проекта – открытие новых знаний.

Учащиеся в группах продумывают, как, в какой последовательности они будут «накладывать» треугольники, чтобы убедиться, что они равны; после этого ход доказательства обсуждается в классе (учащиеся разных групп как бы делают шаги поочередно).

ДАНО:

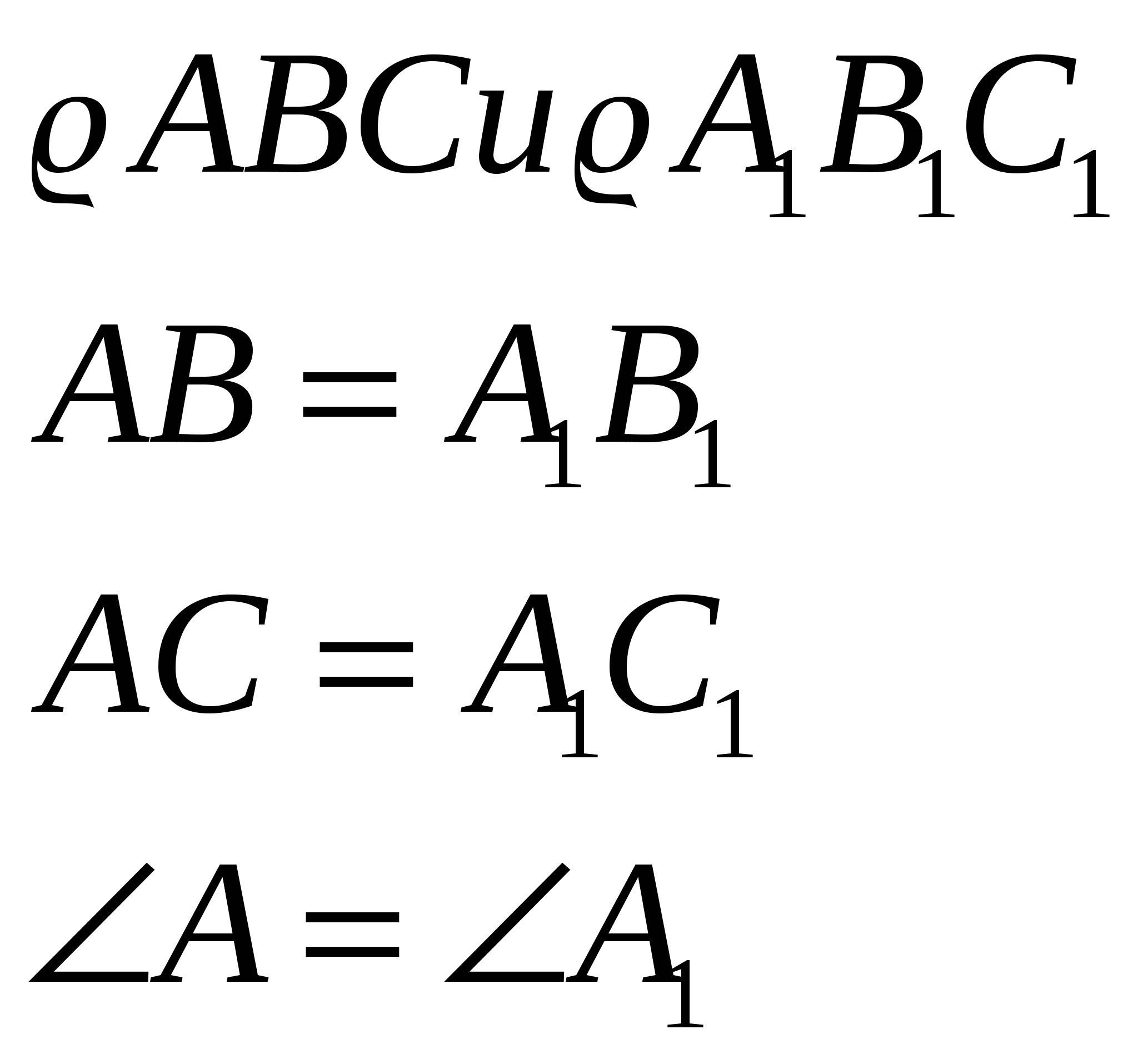
ДОКАЗАТЬ:

РЕШЕНИЕ:

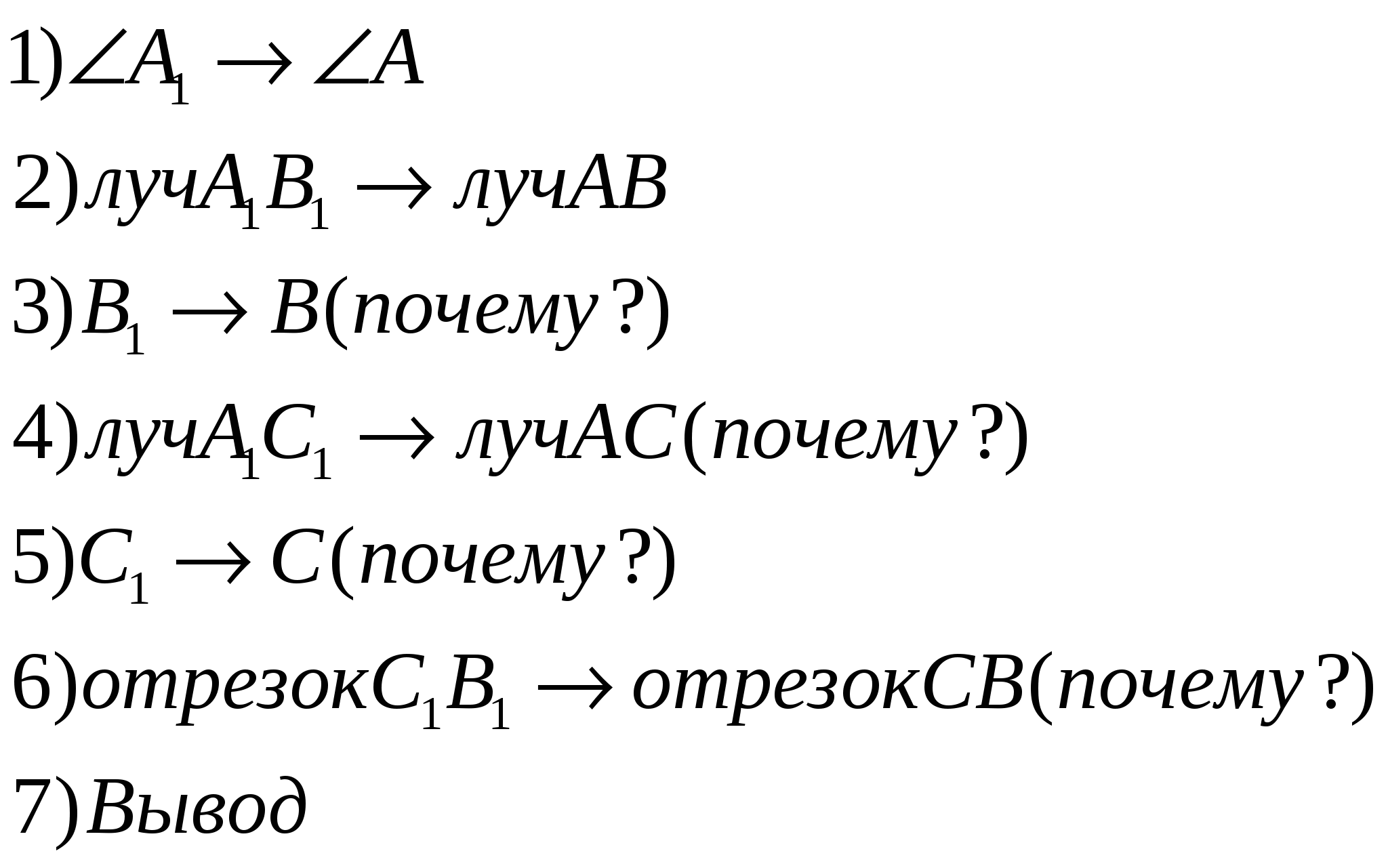
ШАГ 6 – первичное закрепление с проговариванием во внешней речи.

Работа в парах. Обучающиеся проговаривают:

1. формулировку теоремы;

2. доказательство теоремы, поменяв обозначения, делая ходы поочередно.

Самостоятельная работа с проверкой по эталону.

В рабочих тетрадях на печатной основе заполнить пропуски в формулировке теоремы и доказательстве первого признака равенства треугольников. Затем сравнить по эталону.

Э Т А Л О Н

Заполните пропуски в формулировке и доказательстве первого признака равенства треугольников.

Теорема. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Дано: 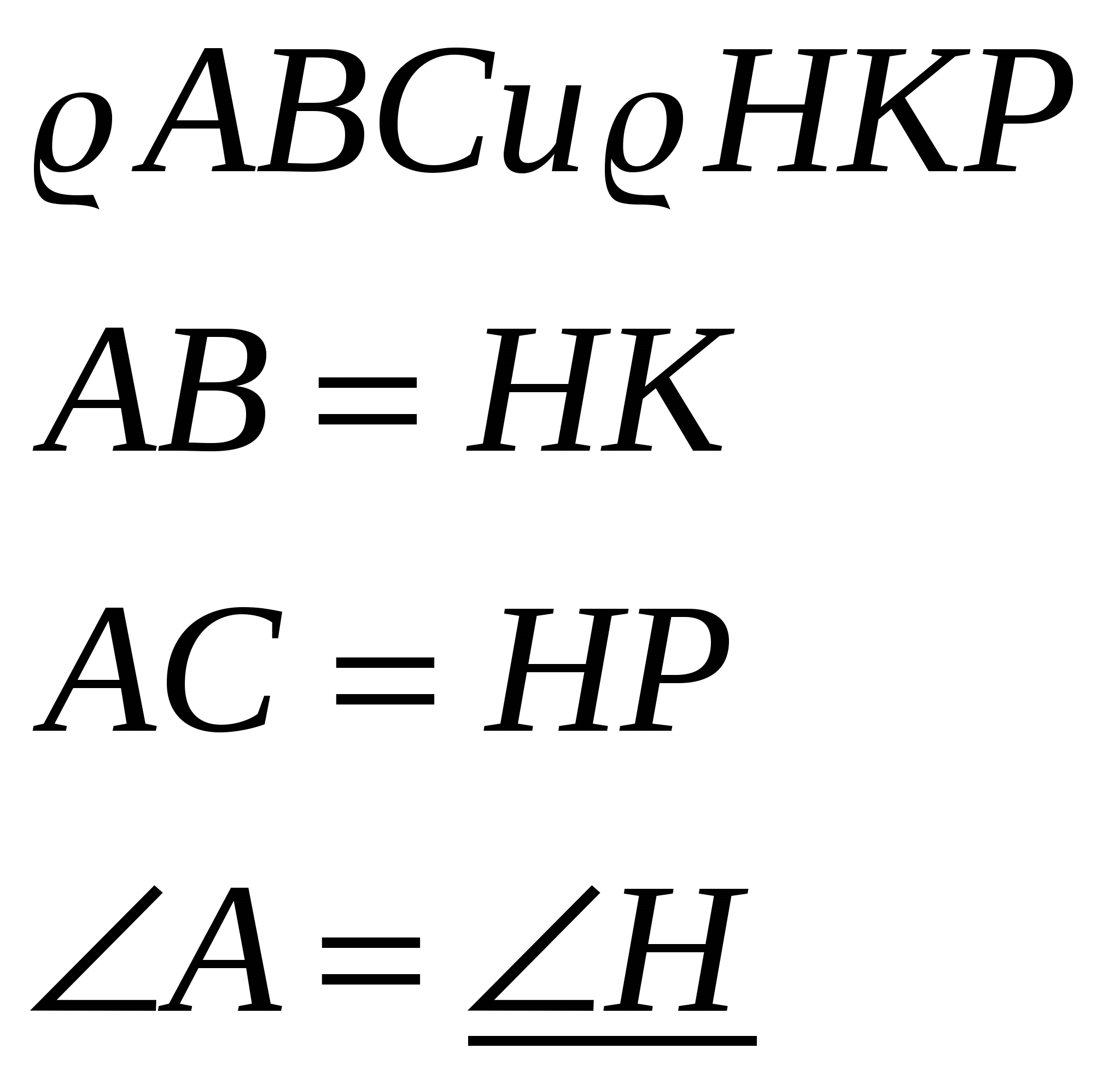Доказать:

Доказательство:

1. По условию теоремы 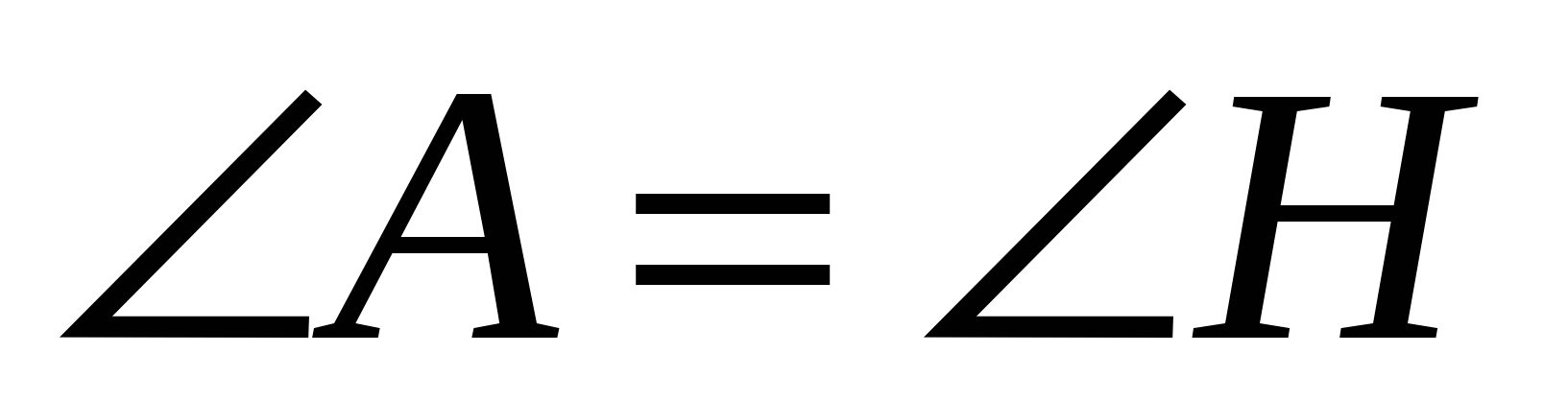, поэтому треугольник АВС можно наложить на

треугольник НКР так, что вершина А совместится с вершиной Н, а стороны АВ и АС наложатся соответственно на лучи НК и НР.

2. По условию АВ=НК, АС=НР, следовательно, сторона АВ совместится со стороной

НК, а сторона АС – со стороной НР, в частности, совместятся точки В и К, С и Р. Поэтому, совместятся стороны ВС и КР.

3. Итак, треугольники АВС и НКР полностью совместятся, значит, они равны. Теорема доказана.

Учитель: Проведите самооценку, сравнив с эталоном. Максимум 3 балла.

Заключительный этап – применение и рефлексия.

ШАГ 7 – включение в систему знаний и повторение.

Устные задачи по готовым чертежам.

ШАГ 8 – самостоятельная работа с проверкой по эталону.

Учитель: Оценим самостоятельную работу, сравнив с эталоном – по 1 баллу за каждый заполненный столбик. Максимум 3 балла.

ШАГ 9 – рефлексия учебной деятельности на уроке.

Найти на чертеже равные треугольники. (На экран проецируются различные треугольники с подписанными тремя парами элементов. Таких треугольников две пары).

Учитель: Оценим результат – по 1 баллу за каждый правильный ответ. Максимум 2 балла.

Итоги урока:

• «Какие открытия вы сделали сегодня на уроке?»;

• «Что научились делать?»;

• «Сколько способов вы знаете, чтобы определить, равны ли треугольники?»

Домашнее задание…….

Оценки за урок:

• Домашнее задание – максимум 3 балла.

• Доказательство теоремы в рабочей тетради – 2 балла.

• Самостоятельная работа – 3 балла.

• Экспресс – диагностика – 2 балла.

• Итого – максимум – 10 баллов.

Ключ к оценке:

9-10 баллов - «5»

7-8 баллов – «4»

5-6 баллов – «3»

ЛИТЕРАТУРА:

1. Н.Г.Кудрявцева «Системно-деятельный подход как механизм реализации ФГОС нового поколения»

2. Л.С.Атанасян «Геометрия 7-9»