Конспект урока «Механика» по физике

йцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъфывапролджэячсмитьбюйцукенгшщзхъчсмитьбюйцукенгшщзхъфывапролджэячсукенгшщзхъфывапролджэячс

Механика

Конспект учителя

2011

Минаков К.С.

« В наш век образованные люди, даже не занимаясь наукой должны знать и понимать физику, и эти блага познания они сохранят как часть своего интеллектуального багажа на всю жизнь. Образованные люди видят, что научные знания влияют на интересы, перспективы и философию.

… Глубина изучения предмета приходит в результате самостоятельных рассуждений и критического мышления, изучение должно в большей степени порождать вопросы, нежели преподносить готовые выводы»

Эрик Роджерс, профессор Принстонского университета.

Механика (греч. Mechanike- орудие, машина) – наука, изучающая перемещения в пространстве (механическое движении) и равновесие материальных тел под действием сил. Часто эту науку называют классической механикой или ньютоновской.

В своем сочинении «Физика» Аристотель (4 век до н.э.) впервые ввел в науку термин «механика». Знание механики прежде всего необходимо для познания окружающего нас мира, так как любое явление в мире связано с движением. По существу, ни одно явление природы не может быть понято без знания механики.

Все на свете движется. Ледник может течь с ледяным спокойствием, перемещаясь на какой-нибудь метр за неделю. Если теннисный мяч выронить в пустоте, то на расстоянии 1 метр он наберет скорость почти 5 метров в секунду. Если электрон, но не мяч, поместить между металлическими пластинами в вакууме, к которым подсоединена батарейка с напряжением 1,5 вольта, он будет разогнан до скорости почти 10⁶ метров в секунду. Это очень большая скорость, особенно в сравнении со скоростью пассажирского самолета, которая равна примерно 300 метров в секунду, и неизмеримо больше скорости пешехода, который движется со скоростью 1,5 метра в секунду.

Но скорость должна «говорить» не только о том, как быстро движется что-то, но и в каком направлении. Однако одной скорости, конечно, не достаточно для описания движения. Скорость служит мерой того, насколько быстро изменяется положение тела, но часто требуется ещё знать, как быстро изменяется сама скорость- это позволяет сделать ускорение.

Классическая механика содержит три раздела: статика или учение о силах, в котором изучаются условия равновесия твердых тел; кинематику или учение о формах движения без выяснения причин этого движения; и динамику или учение о влиянии сил на движение тел, т.е. выясняется причина возникновения ускорения.

Основная задача механики – определять положение тела в любой момент времени.

Движение – неотъемлемое свойство материи

Всё, что реально существует в мире, всё, что нас окружает: сооружения, живые организмы, вода, воздух, свет, атомы, электроны, радиоволны, т.е. все, что мы можем ощущать непосредственно или с помощью специальных приборов, в науке называют материей. Материя существует в двух видах: вещество и поле. Одно из основных свойств материи – движение. Нет и не может быть абсолютно неподвижных тел. Самый простой вид движения – это механическое движение.

Механическим движением тела называют изменение с течением времени его положения в пространстве относительно других тел.

Система отсчёта

Движущееся тело с течением времени изменяет свое положение относительно других тел. Тело, относительно которого изучается движение рассматриваемого тела, называют телом отсчёта. Для описания движения надо знать, как изменяется с течением времени положение тела относительно выбранного тела отсчета. Для этого необходима система координат и таймер. Начало координат совмещают с телом отсчета.

Тело отсчёта, система координат, связанная с ним, и прибор для измерения времени (таймер) образуют систему отсчёта.

Пространство и время

В физике, и в частности, в механике, исключительно важную роль играют пространство и время.

Всё, что существует в мире, существует в пространстве. Нет и не может быть ни одного объекта, который сам не занимал бы пространства и существовал бы вне пространства. Пространство неразрывно связано с материей; пространство объективно существует; пространство бесконечно и протяжённо; пространство трёхмерно (все физические объекты имеют длину, ширину и высоту).

Тела движутся, т.е. изменяют свое положение не только в пространстве, но и во времени. В механике Ньютона, как и в повседневной жизни, время течёт равномерно. Основные свойства времени: время объективно существует; время непрерывно; время одномерно (время течёт только вперед – от прошлого к будущему). Время неразрывно связано с материей, движением и пространством.

В Международной системе единиц (СИ) длина и время являются основными величинами. Единица измерения длины – метр (м) и единица измерения времени – секунда (с).

Название единицы длины происходит от греческого слова metron – измерять.

Единица времени в английском языке в давние времена называлась вторичной минутой – second minute, теперь для краткости говорят просто «секунда».

Некоторые важные понятия

Материальная точка. Любое материальное тело имеет конечные определенные размеры. Но для упрощения исследования движения вводят абстрактное понятие материальной точки.

Материальная точка – это тело, размерами и формой которого в рассматриваемом случае можно пренебречь.

Практика показывает, что такая модель применима к телам, форма и размеры которых несущественны при рассмотрении данного движения, а в случае системы тел – если их размеры малы по сравнению с расстояниями между этими телами.

Траектория.

Непрерывную линию, которую описывает движущееся тело (рассматриваемое как материальная точка) называют траекторией.

В зависимости от траектории движение может быть прямолинейным или криволинейным. Траектория одного и тоже движения неодинакова в различных системах отсчёта. Так, например, в системе отсчёта, связанной с движущимся автобусом или поездом, траектория падения мяча – прямая линия, а в системе отсчёта, связанной с наблюдателем, неподвижно стоящим у дороги или у железнодорожного полотна – кривая линия.

Путь и перемещение.

Расстояние, пройденное телом (материальной точкой) вдоль траектории движении, называют путем S. Перемещением называют направленный отрезок, соединяющий начальное и конечное положение тела, т.е. вектор .

Величины, для которых характерно не только численное значение (размер, модуль), но и направления, называют векторными (лат.vector – везущий, несущий).

Путь обычно больше модуля перемещения, и только в случае прямолинейного движения в одном направлении путь равен модулю перемещения.

Величины, для которых нехарактерно направление и имеющие только размер, называют скалярными (лат. scalaris – ступенчатый).

Путь величина скалярная, а перемещение - векторная.

Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчёта, т.е. механическое движение относительно.

Поступательное и вращательное движение

Часто можно наблюдать такое движение, при котором все точки тела движутся по одинаковым траекториям. Так движется пила при распиливании дров, кузов автомобиля на дороге без поворотов и т.п.

Движение тела, при котором все его точки движутся одинаково, называется поступательным.

Второй вид движения – вращательное, при котором траектория точек тела – окружности, центры которых лежат на общей прямой (например, стрелки часов, сверло и т.п).

В природе и технике часто встречаются движения, которые можно представлять в виде сочетания поступательного и вращательного движений (например, движение колес поезда относительно поверхности Земли).

Прямолинейное равномерное движение

Равномерным движением называют такое движение, при котором тело за любые равные промежутки времени проходит соответственно равные расстояния.

Скорость

Для количественной характеристики процесса движения тела вводится понятие скорости движения .

Скоростью движения называют векторную физическую величину, характеризующую быстроту (стремительность) движения.

Скорость равномерного движения равна отношению перемещения тела ко времени, за которое это перемещение произошло:

=

Для того чтобы найти модуль скорости, формулу надо написать в скалярной форме через модули входящих в формулу векторных величин.

=

В СИ единицей расстояния является метр, единицей времени – секунда; поэтому скорость выражается в метрах в секунду (м/с).

Перемещение

Зная скорость можно вычислить перемещение за любой промежуток времени

=

При вычислениях перемещения и скорости пользуются формулами, в которые входят не векторы, а их проекции на оси (или ось) координат. Проекции векторов – величины скалярные, поэтому над ними можно производить алгебраические действия. В случае прямолинейного движения проекция векторов перемещения и скорости на траектории движения совпадают с алгебраическим значением этих величин:

= S =

X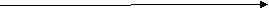

В обычной и в научной речи, чтобы не загромождать ее термином «модуль» под словами «расстояние» и «путь» понимается модуль перемещения, а под словом скорость имеется ввиду модуль скорости.

Относительность движения

Если рассмотреть движение одного и того же тела в различных системах отсчёта, то получатся разные результаты, например: в системе отсчёта связанной с вагоном пассажир находится в покое, а относительно системы отсчёта, связанной с землей, движется. Поэтому в физике говорят: движение относительно. В эту фразу вкладывается тот смысл, что движение всегда рассматривается относительно какой-то системы отсчёта.

Классический закон сложения скоростей

Рассмотрим пример, когда по прямолинейному участку железнодорожного пути движется вагон с постоянной скоростью относительно земли. В это же время пассажир движется по вагону в том же направлении со скоростью относительно вагона. Тогда скорость пассажира относительно земли равна:

=

Если пассажир движется в противоположном направлении, то в формуле знак «плюс» меняется на «минус».

Графическое представление движения

Во многих случаях движение тел, например, железнодорожных поездов, удобно изображать в виде графиков. Для построения графика скорости используют прямоугольную систему координат, по горизонтальной оси которой откладывают в определенном масштабе время, а по вертикальной – модуль скорости. Так как при равномерном движении скорость – величина постоянная, график скорости представляет собой прямую параллельную оси времени. С помощью графика скорости можно определить пройденное телом расстояние. Так как S=t , то это произведение численно равно площади прямоугольника, сторонами которого служат оси координат.

Прямолинейное неравномерное движение

Часто приходится иметь дело с такими движениями, при которых скорость изменяется со временем. Такие движения называются неравномерным.

При неравномерном движении определять перемещение по формуле S= t уже нельзя, потому что скорость в разные моменты времени различна.

Средняя скорость

В некоторых случаях, когда имеют дело с неравномерным движением, пользуются средней скоростью на всем пути: =

Знание средней скорости позволит найти перемещение по формуле:

S = t

Если известны средние скорости на нескольких участках всего пути, то можно вычислить среднюю скорость для всего пути по формуле:

=

(сумма длин всех участков пути делится на сумму всех отрезков времени).

Мгновенная скорость

Скорость тела может непрерывно изменяться, а для изучения движения часто важно знать скорость именно в данный момент времени или, как принято говорить, важно знать мгновенную скорость тела.

Мгновенной скоростью называют скорость в данный момент времени.

Мгновенная скорость равна отношению очень малого перемещения к промежутку времени, в течение которого это перемещение совершилось:

=

Мгновенная скорость - величина векторная. Ее направление совпадает с направлением перемещения.

Прямолинейное равноускоренное движение

При неравномерном движении мгновенная скорость тела непрерывно изменяется от точки к точке, от одного момента времени до другого. Для вычисления перемещения, т.е. координаты тела в любой момент времени нужно знать, как быстро она изменяется, т.е. каково ее изменение за единицу времени.

Для простоты рассмотрим такое неравномерное движение, при котором скорость тела за каждую единицу времени и вообще за любые равные промежутки времени изменяется одинаково. Такое движение называют равноускоренным.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называется равноускоренным движением (если скорость уменьшается, то движение можно назвать равнозамедленным).

Процесс изменения скорости тела характеризуется ускорением.

Ускорением называют векторную физическую величину, характеризующую скорость изменения скорости. Ускорение определяется отношением изменения скорости движения ко времени, за которое это изменение произошло:

=

За единицу ускорения в СИ принят метр на секунду в квадрате (метр в секунду за секунду), м/.

Зная начальную скорость тела и его ускорение , можно найти скорость тела в любой момент времени:

= + t

либо:

= + a t

= - a t (для равнозамедленного движения)

Из данной формулы для скорости видно, что мгновенная скорость равноускоренного движения линейно зависит от времени:

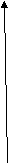
t

Перемещение при прямолинейном равноускоренном движении

Путь, пройденный телом при равноускоренном движении можно подсчитать по формуле:

= t ±

(«+» - скорость увеличивается, « - » - скорость уменьшается)

Если тело трогается с места ( = 0), то: =

Другая формула для вычисления перемещения:

S =

Если = 0, то:

S =

Свободное падение тел

Свободным падением называют падение тел в вакууме, когда их движению не мешает воздух.

Изучение свободного падения можно проводить на опыте с падением достаточно массивного стального шарика в воздухе. Конечно, воздух будет оказывать движению шарика сопротивление, но, как показывают наблюдения, если шарик массивный, то это сопротивление заметно не влияет на его движение и им можно пренебречь.

В конце XVI века Галилео Галилей установил, что свободное падение равноускоренное. Ускорение этого движения одинаково для всех тел и по модулю равно 9,81 м/. Чтобы отличать свободное падение от всех других ускоренных движений, принято ускорение свободного падения обозначать буквой «g» вместо «а».

На экваторе g несколько меньше, а на Северном полюсе несколько больше значения 9,81 м/.

Когда тело падает с большой высоты в воздухе, его скорость не возрастает неограниченно. Сопротивление воздуха становится все больше и больше, пока не исчезает ускорение, после чего тело начинает падать с постоянной скоростью. Например, для человека эта предельная скорость равна, примерно, 60 м/с (около 200 км/ч).

Криволинейное движение

Равномерное движение по окружности

Часто движение происходит по кривым линиям. Изучить все виды криволинейных движений невозможно, да и нет в этом необходимости. Почти любое криволинейное движение можно представить как последовательность движений, происходящих по дугам окружностей.

Примерами движения тела по окружности могут служить движения искусственного спутника, обращающегося вокруг Земли по круговой орбите; движение какой-либо точки на вращающемся теле (например, колесе). Наглядные ощущения человеку о движении по окружности может дать катание на аттракционе «цепочная карусель».

Основные характеристики движения по окружности

1. Угловое перемещение φ - это угол, который описал радиус, проведенный из центра окружности к материальной точке за время ее перемещения из точки А в точку В. Угловое перемещение в СИ выражают в радианах.

2. Частота обращения - это число оборотов материальной точки вокруг центра обращения за секунду:

ν = ,

где N – число оборотов.

За единицу частоты обращения принят оборот в секунду (с^-1)

3. Период обращения – это время, в течение которого совершается один оборот точки по окружности:

T =

За единицу периода принята секунда (с).

Период и частота – величины взаимно обратные:

ν = ; T =

4. Угловая скорость – это отношение углового перемещения к промежутку времени, за которое это перемещение совершено:

ω =

Единицей угловой скорости в СИ является радиан в секунду (рад/с).

Угловое перемещение φ за период Т равно 2π. Следовательно, угловая скорость равна:

ω = или ω = 2πν

5. Линейная скорость .

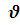Линейная скорость тела, движущегося по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлено по касательной к траектории. Так как S = t, то за один оборот ( t = T) тело пройдет расстояние S = 2πr. Поэтому:

= или = 2πrν ;

Также: = ωr или ω =

6. Центростремительное ускорение a.

При равномерном движении тела по окружности его линейная скорость, оставаясь постоянной по модулю, непрерывно изменяется по направлению. Но изменение скорости по направлению свидетельствует о том, что при равномерном движении по окружности есть ускорение, которое и является причиной непрерывного изменения направления скорости. Это ускорение получило название центростремительного, т.е. направленного по радиусу окружности к ее центру. В любой точке вектор ускорения перпендикулярен вектору скорости. Модуль центростремительного ускорения равен: a = .

Равномерное движение по окружности нельзя назвать равноускоренным, так как направление ускорения от точки к точке изменяется.

Используя предыдущие формулы можно получить другие формулы для вычисления ускорения:

a = или a =

Часто центростремительное ускорение называют нормальным, т.е. перпендикулярным к скорости.

Повторение координат

Главная особенность движения по окружности – координаты тела через каждый период обращения повторяются.

Равномерное движение по окружности – это периодическое движение, следовательно, так же периодически изменяются и численные значения и направления скорости и ускорения. Такого рода периодические изменения величин называют колебаниями.

Некоторые моменты дифференциального исчисления в механике

1. Средняя скорость 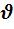= не может описать характер движения на отдельных участках траектории. Чтобы отразить этот характер вводится понятие мгновенной скорости – скорости в данный момент времени.

Предел отношения при неограниченном уменьшении промежутка времени , называется мгновенной скоростью (или просто скоростью):

= = ,

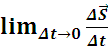где - производная от вектора перемещения по времени.

Таким образом можно сказать: скоростью ( или мгновенной скоростью) называется векторная величина, равная первой производной по времени от вектора перемещения.

2. Для характеристики быстроты изменения вектора скорости в механике вводится понятие ускорения.

Ускорением (или мгновенным ускорением) называется векторная величина , равная первой производной по времени от скорости или, что то же самое, второй производной по времени от вектора перемещения :

= =

Динамика

Динамика (от греческого слова dynamis – сила) – раздел механики, в котором изучается движение тел в связи с их взаимодействием с другими телами.

Динамика объясняет, при каких условиях тело движется так, а не иначе, когда тело движется равномерно и когда равноускоренно, когда тело движется прямолинейно и когда криволинейно.

Основой динамики являются законы движения тел, сформулированные Исааком Ньютоном в его работе «Математические начала натуральной философии», опубликованной в 1687 году.

Поэтому динамику называют ньютоновской в отличии от галилеевской кинематики.

Сила и движение.

Человечеству потребовалось шестнадцать столетий, чтобы прийти к пониманию движения.

В окружающем нас мире все находится в непрерывном движении и изменении.

Движение – неотъемлемое свойство материи. Нет и не может быть материи без движения и движения без материи.

Под словом «материя» мы понимаем все то, что реально (действительно) существует независимо от нашего сознания, т.е. не является продуктом нашего ума или воображения. Атомы, молекулы, различные тела в твердом, жидком или газообразном состоянии, представляющие собой собрания атомов и молекул, вся «живая» и «неживая» природа – вот разнообразные виды материи.

В результате взаимодействия движение тел может измениться. Для того чтобы глубже понять законы движения надо изучить взаимодействие тел друг с другом, потому что взаимодействие, также как и движение - неотъемлемое свойство материи.

Взаимодействие тел. Сила.

С взаимодействием тел мы сталкиваемся на каждом шагу. Собственно и каждый шаг мы делаем, взаимодействуя (отталкиваясь) с Землей. Хоккейная шайба, взаимодействуя с клюшкой хоккеиста, изменяет направление своего движения. Человек, открывая дверь, растягивает пружину, в этом случае взаимодействие рук и пружины приводит к деформации пружины. А затем взаимодействие пружины и двери приводит к закрыванию последней, т.е. (приводит к движению двери). Вообще, примеров взаимодействия бесконечная величина.

Взаимодействие тел может происходить различными способами. Например, одну и ту же пружину ребенок растянет меньше, чем взрослый человек.

Для характеристики взаимодействия тел в физике введена особая величина – СИЛА.

Понятие силы первоначально применялось для описания мускульных усилий человека, а позже перешло в науку. Так как при взаимодействии тел может изменяться скорость движения, то силе приписывают направление, совпадающее с направлением ускорения, которое тело получает в результате взаимодействия. Прямую линию, вдоль которой действует сила, называют линией действия силы.

Силой называют векторную физическую величину, характеризующую механическое действие одного тела на другое и являющуюся мерой этого действия.

Тому, что мы понимаем под силой, можно дать практическое определение, описывая способ ее измерения. Метод измерения может быть основан на производимых силами действиях. Известно два таких действия.

Во-первых, приложенная к телу сила может вызвать его деформацию (растяжение, скручивание, изгиб);

Во-вторых, приложенная к телу сила может изменить его скорость - ускорить, замедлить или изменить направления его движения.

Мы узнаем о существовании силы, если объект оказывается деформированным или подверженным ускорению.

Сила не может возникнуть из ничего и действовать только на это тело. Сила может существовать только как взаимодействие между двумя телами.

Единицей измерения в СИ служит ньютон (Н). Эта единица будет что- то значить для вас, только если ваши мышцы познакомятся с ней: литр молока или воды весят около 10Н.

Механическое взаимодействие может осуществляться как при непосредственном контакте тел (например, при трении, при давлении тел друг на друга), так и между удаленными телами (посредством особой формы материи, которая называется физическим полем или просто полем).

Все взаимодействия в природе можно разделить на четыре вида: гравитационное, электромагнитное, сильное (ядерное), и слабое (ядерное), которые называются ФУНДАМЕНТАЛЬНЫМИ ВЗАИМОДЕЙСТВИЯМИ.

В механике обычно учитывают только гравитационное и электромагнитное взаимодействия и соответствующие им гравитационные силы (силы всемирного тяготения) и две разновидности проявления электромагнитных сил - силы упругости и силы трения.

Сложение сил.

Сила – величина векторная, поэтому в том случае, когда на материальную точку действуют несколько сил, они складываются геометрически.

Силу, заменяющую действия на материальную точку нескольких сил, называют РАВНОДЕЙСТВУЮЩЕЙ или РЕЗУЛЬТИРУЮЩЕЙ этих сил.

Равнодействующая сила равна геометрической сумме сил, действующих на материальную точку.

Равнодействующую имеет не каждая система сил. Например, не имеют равнодействующей две равные параллельные силы, направленные в разные стороны или силы, не лежащие в одной плоскости.

Масса.

Современного физика движение интересует тогда, когда оно изменяется. Равномерное движение, по его мнению, продолжается само по себе.

Повседневный опыт свидетельствует о том, что у всех тел есть общее свойство: скорость движение тел, в процессе их взаимодействия, изменяется постепенно и для ее изменения требуется некоторое время. Это свойство тел получило название инертности.

Инертностью называется – свойство тел, проявляющееся в том, что скорость их движения остается неизменной до тех пор, пока на них не подействуют другие тела. В процессе взаимодействия их скорость не может измениться мгновенно, а изменяется постепенно.

Все тела инертны.

Но инертность различных тел разная. Из двух взаимодействующих тел инертность больше у того тела, которое в результате взаимодействия приобретает меньшее ускорение. Например, пуля при выстреле получает большее ускорение, чем ружье. Следовательно, инертность ружья больше инертности пули.

Для характеристики инертности ввели особую величину - массу.

Эту величину также называют «инертной» массой, указывая на то, что она определяет инертность материальной точки по отношению к изменению ее движения. Существует также «гравитационная» или «тяжелая» масса, определяемая законом тяготения.

Но в начале ХХ века удалось постулировать, что между инертной и тяжелой массами нет никакого различия. На этом основании принято говорить просто о массе m материальной точки или тела. Поэтому существует и такое определение:

масса m некоторого тела есть по определению мера количества вещества, содержащегося в этом теле.

Единицей массы в СИ является килограмм (кг).

Немного истории.

Когда во времена французской революции вводилась метрическая система мер, в качестве единицы массы была выбрана масса одного кубического сантиметра воды при её наибольшей плотности (при 4). Такая единица была названа граммом. Для практических целей в качестве эталона был выбран килограмм – 1000 граммов. Эта масса 1000 см³ или одного литра воды. Цилиндр, сделанный из специального сплава платины, обрабатывали и полировали до тех пор, пока он не уравновешивался на чашке весов литром воды.

Эталон был введен на основе представления о гравитационной массе.

Международными соглашениями 1870-72 г.г. принято, что международный килограмм должен быть выведен из «архивного килограмма». Сначала был изготовлен из платино-иридиевого сплава один эталон килограмма, который и был признан международным эталоном (прототипом). Он хранится в Международном бюро мер и весов в г. Севре (близ Парижа). Затем было изготовлено еще 42 эталона. При распределении эталонов килограмма Россия получила два эталона (№ 12 и № 26).

Эталон № 12 равен 1 кг + 0,668 мг ± 0,002 мг.

Эталон № 26 равен 1 кг – 0,032 мг ± 0,002 мг.

Несколько неудачно то, что название основной единицы – килограмм – массы выражается как кратное вспомогательной единицы – грамма. В 60-е годы ХХ века на нескольких международных совещаниях обсуждался вопрос о переименовании килограмма, но безуспешно.

Важные дополнения.

Аддитивность – это следующее свойство массы: если система тел образовалась от слияния нескольких тел, то её масса равна сумме масс этих тел.

Центр масс – это точка, в которой как бы сосредоточена вся масса тела или системы тел. Понятие центра масс существенно важно при рассмотрении таких вопросов, когда по условиям задачи тело нельзя принять за материальную точку. В этом случае центр масс движется так, как двигалась бы материальная точка с массой, равной массе всего тела. Центр масс может находиться как теле, так и вне его. Например, центр масс трубы находится в середине её оси, но, поскольку труба полая, в этой точке нет вещества.

Масса никогда не меняется. Масса – неизменное свойство всех видов вещества, нечто, существующее столь же вечно, как и сама материя (теорию относительности в данном случае мы не рассматриваем).

Вообще о массе физики рассуждают так: масса представляет собой очевидную меру тяжеловесности вещества (назвать это свойство вещества «инертностью» - просто присвоить ему некоторое наименование).

Весьма точные измерения, проводимые в ядерной физике, показывают, что излучение света или тепла сопровождается ничтожной потерей массы излучающего вещества. Если же этот свет поглощается каким-нибудь другим веществом, то это вещество настолько же увеличивает свою массу, насколько излучающее тело уменьшает ее. Таким образом, в этом масштабе сохранение массы соблюдается. Только в ядерных лабораториях и в грандиозных естественных ядерных реакторах – внутри звезд – происходят изменения, в которых масса превращается в излучения в заметных количествах.

Законы движения

Законы движения макроскопических тел впервые были сформулированы в 1686 году Исааком Ньютоном (1643-1727) и носят его имя. Он сумел окончательно связать понятие силы и инертной массы с помощью трех законов:

Закона инерции;

Основного закона динамики;

Закона равенства действия и противодействия.

Первый закон описывает свободные движения, на которые не действуют силы.

Второй закон определяет силу через производимые ею изменения движения тела.

Третий закон определяет соотношение между силами и совместное действие сил.

Первый и второй законы были частично высказаны еще до Ньютона (Галилео Галилей, Христиан Гюйгенс); третий закон впервые открыл Ньютон.

Исаак Ньютон создал законченную теорию механического движения, которая впоследствии только уточнялась. Он писал в одном из своих писем английскому физику Р.Гуку: «Если я видел дальше, чем другие, то лишь потому, что стоял на плечах гигантов».

Первый закон Ньютона (Закон инерции).

Впервые всесторонний и глубокий анализ движения и относительно покоя провел Галилео Галилей и пришел к выводу, что в том случае, когда на тело не действуют другие тела, оно либо находится в покое, либо по инерции движется прямолинейно и равномерно.

До Галилея господствовало учение греческого ученого Аристотеля, который утверждал, что тело движется только тогда, когда на него действуют другие тела (силы).

Ньютон был убежден в правоте Галилея и включил закон инерции в систему законов движения, сформулировав его следующим образом:

Всякое тело сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока оно не будет вынуждено изменить это состояние в результате действия сил.

Этот закон называют законом инерции или первым законом Ньютона.

Для понимания этого закона требуется смелая абстракция, так как все встречающиеся в природе движения возмущаются различными силами, например, трением или гравитацией.

Тела могут находиться в относительном покое или двигаться прямолинейно и равномерно и в том случае, когда действие на них других тел уравновешено.

Второй закон Ньютона (Основной закон динамики).

На вопрос о том, что произойдет с телом в результате его взаимодействия с другими телами, дает ответ второй закон Ньютона. Он является основным законом движения и включает в себя первый закон Ньютона и предполагает выполнение третьего при любой экспериментальной проверке. Этот закон, связывающий силу, ускорение и массу, чрезвычайно важен для других разделов физики и экспериментально подтверждается для движения всех макроскопических тел.

Если действовать одинаковой силой на тела разной массы, то можно прийти к выводу, что ускорения, которые получают эти тела, обратно пропорциональны массам:

a (F=const)

Если действовать на одно и то же тело разными силами, то опыт показывает, что ускорение тела прямо пропорционально силе:

a (m=const)

Указанные опыты и множество других показывают, что если на разные тела действует одна и та же сила, то величина, равная произведению массы тела на его ускорение, остаётся одной и той же. Это и позволило Ньютону сформулировать основной закон движения, называемый сейчас вторым законом Ньютона:

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:

F=ma

На тело может действовать несколько сил. Ускорение в этом случае оказывается таким, какое ему сообщило бы одна – единственная сила, равная геометрической сумму всех приложенных сил (равнодействующая).

На основе второго закона Ньютона устанавливается единица силы. За единицу силы принимается сила, сообщающая телу массой 1кг ускорение 1 м/с². Эта единица называется ньютон:

1Н =

Системы отсчёта в динамике.

При изучении кинематики имеется свобода выбора системы отсчета – не имеет значения, движется ли система отсчета прямолинейно и равномерно или ускоренно. В динамике дело обстоит иначе.

Если система отсчета движется относительно системы К, в которой тело покоится или движется равномерно, то относительно системы тело движется ускоренно, хотя на него и не действуют другие тела или силы. Следовательно, в системе отсчета, движущейся с ускорением, закон инерции несправедлив.

Таким образом, закон инерции справедлив в одной системе отсчета и несправедлив в другой.

Системы отсчета, в которых справедлив закон инерции, называют инерциальными системами отсчета.

Второй закон Ньютона так же, как и первый, справедлив только для инерциальных систем отсчета.

Второй закон Ньютона в импульсной форме (вычисление силы по изменения количества движения – импульса).

Предположим, что нужно решить две задачи:

А. Снаряд массой 1 кг движется горизонтально со скоростью 600 м/с. Какую силу он развивает?

В. Десятитонный грузовик, движущийся со скоростью 48 км/ч, врезается в стену и останавливается. Какова сила столкновения?

Эти вопросы кажутся разумными, да и ответ на них как будто имеет важное значение. На самом деле в той форме, в какой эти вопросы поставлены, они бессмысленны. Движущийся снаряд не создает усилия в направлении своего движения и не нуждается в приложении силы, чтобы двигаться. Неизменное движение не связано ни с какой силой, а чтобы придать телу ускорение, к нему нужно приложить силу из вне. Даже зная изменение скорости, как в задаче В, нельзя ответить на поставленный вопрос, так как неизвестно, за какой промежуток времени происходит это изменение скорости, и, следовательно, нельзя вычислить ускорение.

На практике ни один инженер или физик не в состоянии создать прибор для измерения «силы» снарядов в полете. Прикрепленные к снаряду пружинные весы вообще не показывают никакой силы, пока снаряд движется свободно. Мгновенные фотографии самого снаряда не обнаружат никакой деформации. А поскольку попытки измерить «силу» не дают результата, нельзя считать понятие «силы» в этом случае сколько-нибудь полезным. Если же движущийся грузовик или снаряд сталкиваются с чем-нибудь и изменяют скорость, то это связано с реальной силой, с усилием, которой можно почувствовать или с чем-то таким, что можно измерить или обнаружить по деформации. Например, фотографии снаряда, снятые во время столкновения его со стальной стеной, обнаруживают заметное сжатие и используются для оценки действовавшей силы.

В приведенной выше «задаче В» известна масса, но не известно ускорение. Но если известна продолжительность столкновения, т.е. даны масса, изменение скорости и время, то соотношение F = ma можно изменить так, чтобы в него входили F, Δt, m и Δ :

F= ma →FΔt =ma Δt→ FΔt = m Δ → F Δt = m (- ) →

F Δt = m-m

Величина р = m называется импульсом тела или количеством движения.

Величина I = FΔt называется импульсом силы.

Используя эти два понятия второй закон Ньютона можно сформулировать следующим образом:

Импульс сил, приложенных к телу равен изменению импульса тела (количеству движения)

F Δt = Δр

В СИ единицей измерения импульса силы является Н ∙с, а единица импульса тела .

Вот каким образом соотношение F= ma приобретает тот вид, который фактически был дан Ньютоном.

Третий закон Ньютона (закон равенства действия и противодействия).

Ни первый, ни второй законы Ньютона не говорят о том, что происходит со вторым взаимодействующим телом. Об этом идет речь в третьем законе.

Действия тел друг на друга всегда имеют характер взаимодействия. Каждое из тел действует на другое и сообщает ему ускорение. Ньютон сформулировал третий закон следующим образом:

Действию всегда есть равное и противоположное противодействие, иначе – действия двух тел друг на друга между собой равны и направлены в противоположные стороны.

Ньютон под терминами «действие» и «противодействие» понимал силы, с которыми взаимодействующие тела действуют друг на друга. Поэтому третий закон можно сформулировать так:

Силы, с которыми взаимодействующие тела действуют друг на друга, направлены по одной прямой, равны по модулю и противоположны по направлению.

Математически это записывается в таком виде:

= или m₁ = m₂

Этот закон отражает тот факт, что в природе нет и не может быть одностороннего действия одного тела на другое, а существует только взаимодействие. Силы действия и противодействия появляются одновременно, парами. Иногда эту мысль выражают так: нет действия без противодействия.

Важно подчеркнуть, что силы взаимодействия хотя и равны, и противоположно направлены, но не уравновешивают друг друга, так как приложены к разным телам. Например, когда человек идет по Земле, то сила, с которой он отталкивает Землю, равна той силе, с которой его толкает вперед Земля. Однако эти силы не уравновешиваются; согласно второму закону динамике они сообщают человеку и Земле ускорения обратно пропорциональные их массам. Но Земля благодаря ее очень большой сравнительно с человеком массе остается при этом практически неподвижной, а человек движется.

Так же как первый и второй законы, третий закон Ньютона справедлив только для инерциальных систем отсчета.

Законы Ньютона и относительность движения.

Законы Ньютона верны, если рассматривать движение относительно инерциальной системы отсчета. Инерциальных систем отсчета имеется бесчисленное множество. Что произойдет, если заменить одну инерциальную систему отсчета другой?

Сила, приложенная к телу, не может измениться. Не может измениться и масса тела. Точно также от выбора системы отсчета не может зависеть и ускорение. А так как, кроме силы, массы и ускорения никакие другие величины в законы Ньютона не входят, то можно утверждать, что законы механического движения одинаковы для всех инерциальных систем отсчета.

Это утверждение называется принципом относительности Галилея.

Он означает, что законы механики одинаковы во всех инерциальных системах отсчета, т.е. в разных инерциальных системах отсчета все механические процессы протекают одинаково.

Никакие механические эксперименты, проведенные в замкнутой системе тел, не позволяют установить, покоится эта система или движется равномерно и прямолинейно. Например, глядя в окно своего вагона, человек не может определить, его поезд движется или соседний, пока его поезд покоится или движется равномерно и прямолинейно.

Немного истории.

Основные законы динамики, составляющие фундамент классической механики, изложены Ньютоном в труде под названием; «Philosophiae Naturalis Principia Mathematica» («Математические начала натуральной философии»), вышедшей в 1687 году. Первый русский перевод был сделан академиком А.Н.Крыловым в 1915-1916 годах.

Вот как выглядят эти законы в оригинале и в русском переводе:

Lex I Corpus omne perseverare in statu suo quiescende vel movendi uniformiter in directum, nisi quantenus illud a viribus impressis cogitur statum suum mutare. – Всякое тело сохраняет свое состояние покоя или равномерного прямолинейного движения, пока и поскольку не понуждается приложенными силами изменять это состояние.

Lex II Mutationem motus proportionalen esse vi motrici impressae et fiery secundum lineam rectam, qua vis illa imprimitur. – Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.

Lex III Actioni contrariam sеmper et aequalem esse reactionem, sive corporum duorum actions in se mutuo simper esse aequales et in partes contrarias dirigi.- Действию всегда соответствует равное и противоположное противодействие, другими словами: действие двух тел друг на друга всегда равны и направлены в противоположные стороны.

Закон всемирного тяготения

Ньютон сформулировал свои законы так, чтобы иметь возможности пользоваться ими. Обратившись к проблемам астрономии, он сразу же ответил на вопрос, который не могли решить древние греки и который поставил в тупик Кеплера и даже Галилея: «Что удерживает Луну и планеты при их движении по орбитам?» предполагалось все – хрустальные сферы, естественное круговое движение, вращающиеся рычаги и магнитные флюиды, вихри. Ньютон понимал, что такие объяснения содержат детали, в которых нет необходимости. Сила не нужна для движения планет (первый закон). Предоставленные сами себе они будут вечно двигаться прямолинейно. Сила необходима, чтобы планеты двигались по криволинейной орбите, так как если нет силы, то движение будет прямолинейным.

Какой должна быть величина внешней силы? Откуда она может взяться? Это были новые вопросы, поставленные Ньютоном.

Ньютону удалось объяснить, откуда берется эта сила. Он предположил, что силы, заставляющие падать тела на поверхность Земли, могут также притягивать Луну и служить причиной ее движения по круговой орбите.

Существует легенда о том, что Ньютон обдумывал эту проблему, сидя в саду и яблоко, упавшее ему на голову, подсказало решение. Такое притяжение называется «гравитацией» - словом, которое обозначает «тяжесть».

В 1667 году, анализируя материалы астрономических исследований, Ньютон применил сформулированные им законы динамики к движению Луны и высказал предположение, что силой, заставляющей Луну двигаться по круговой орбите, является сила взаимного притяжения Луны и Земли. Произведя необходимые расчеты, он получил формулу для вычисления этой силы. Мало того, он предположил, что по полученной им формуле можно рассчитать силу притяжения любых тел, если их размеры малы по сравнению с расстояниями между ними. Поэтому открытый им закон получил название закона всемирного тяготения.

Закон всемирного тяготения можно сформулировать следующим образом:

Два тела (рассматриваемые как материальные точки), притягиваются друг к другу по прямой, их соединяющей, с силами прямо пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними

F = G

Этот закон справедлив лишь тогда, когда геометрические размеры тел малы по сравнению с расстоянием между ними и их можно принять за материальные точки. Однако закон справедлив и для больших однородных шаров, находящихся на небольших расстояниях. В этом случае следует считать сосредоточенной в их центре.

Гравитационная постоянная.

В формулу закона всемирного тяготения входит гравитационная постоянная G. Она имеет простой физический смысл.

Если массы взаимодействующих тел m₁ и m₂равны единице (1 кг) и расстояние R между ними тоже равно единице (1м), то сила численно равна G.

Единицей измерения G в СИ является .

Численное значение G может быть найдено только из опытов. Такие опыты проводились много раз, начиная с 1740 г. (Буже получил значение G=12∙ 10^-11). Английский физик Генри Кавендиш в опыте со свинцовыми шарами получил значение G=6,75∙ 10^-11 в 1798 г.

Более поздние измерения дали очень точные значение G с ошибками меньше 0,2%. В 1942 году Гейл из Национального бюро стандартов (США) сделал одно из самых надежных измерений этой фундаментальной постоянной. До тех пор, пока какая-либо новая теория не потребует более точных измерений, эксперимент вряд ли будет повторен:

G=6,673∙ 10^-11

В настоящее время большинство физиков рассматривает гравитационную постоянную в качестве такой же истинной постоянной, как скорость света, заряд электрона и т.д., которые одинаковые для всех веществ и при любых условиях.

Гравитационную постоянную иногда удобно считать равной простой дроби: G ≈ ∙ 10^-11

Как осуществляется притяжение?

Вокруг каждого тела существует его своеобразное материальное продолжение – невидимое гравитационной поле, называемое так же полем тяготения. Гравитационное поле вокруг тела не одинаково: оно сильнее всего вблизи тела и постепенно ослабевает по мере удаления от него. Гравитационное поле прямо пропорционально зависит от массы тела. В отличие от электрического поля, которое существует только вокруг наэлектризованных тел и магнитного поля, существующего вокруг проводников с током и магнитов, гравитационное поле существует вокруг всех тел.

Интересна особенность гравитационного поля – оно проникает через все материалы. От электрического поля можно защититься с помощью проводящих электрических заряды экранов, от магнитного – с помощью железных экранов, а от гравитационного поля экранироваться нельзя.

Масса – мера гравитации.

Понятие массы первоначально было введено при изучении инертных свойств тел, как мера этих свойств. В законе всемирного тяготения проявляется другое свойство тел – свойство взаимного притяжения и масса выступает в новой роли – в качестве меры тяготения. Тела с малой массой притягиваются слабее, чем тела с большой массой, находящиеся на таком же расстоянии.

Массу тел, найденную по силе притяжения к другим телам, называют гравитационной массой (или тяжелой). Таким образом, масса одновременно выступает и как мера инертности тел, и как мера их гравитации (притяжения).

Альберт Эйнштейн (1879-1955) постулировал в общей теории относительности (1916 г.), что гравитационная масса равна инертной.

Многочисленные опыты подтвердили это. Следовательно, можно подвести итог всему сказанному о массе: массой называют скалярную величину, характеризующую инертные и гравитационные свойства тел и являющуюся мерой этих свойств.

Силы в природе

Сила тяжести. Вес.

Сила тяжести и вес – два взаимосвязанных понятия.

Любое тело на Земле притягивается к ней. Если Землю считать однородным шаром, то силу притяжения можно рассчитать исходя из закона всемирного тяготения:

F = G

Эта сила приложена к центру массы тела и направлена по радиусу к центру массы Земли.

Каждое тело на Земле участвует в ее суточном вращении вокруг оси. С точки зрения внеземного наблюдателя связанного с инерциальной системой отсчета, на все тела, находящиеся на Земле, действует центростремительная сила F_цс , направленная перпендикулярно оси вращения. Эта сила вызывается притяжением тел к Земле.

Векторную разность между силой притяжения к Земле и центростремительной силой, вызванной его обращением вокруг земной оси, называют силой тяжести:

=

Центростремительная сила мала, так как мала угловая скорость вращения Земли ( = mR). Центростремительная сила зависит от радиуса обращения R , поэтому сила тяжести зависит от географической широты и на всех точках земной поверхности, кроме полюсов меньше силы тяготения.

Но вообще, сила тяжести мало отличается от силы притяжения Земли и модулю и по направлению: ≈ F, следовательно, = mg.

Точку приложения силы тяжести называют центром тяжести тела. Положение центра тяжести тела совпадает с его центром масс.

Сила тяжести сообщает всем телам, находящимся в данном месте земной поверхности на высоте h от нее, одинаковое ускорение свободного падения:

g = G

Из этой формулы следует, что при высотах над Землей в несколько сотен метров ускорение свободного падения можно считать постоянным.

Допустим, что какое-либо тело, лежит на горизонтальной поверхности – опоре. Тело взаимодействует с Землей и, если бы было свободным, то под действием силы тяжести оно падало бы на Землю с ускорением свободного падения g = 9,8 м/с². Но падению тела препятствует опора. Тело и опора взаимодействуют. Тело действует на опору с силой , равной по модулю силе тяжести, а опора на тело – с равной по модулю, но противоположно направленной силой реакции опоры N.

Силу , с которой тело вследствие его притяжения к Земле действует на опору или подвес, называют весом.

Вес – это сила, приложенная к опоре, а не к телу. К телу приложены лишь сила тяжести и реакция опоры, уравновешивающие друг друга.

Как такая сила возникает? На тело на опоре (или на подвесе) действует сила тяжести = mg, направленная вниз. Оно из-за этого начинает действовать на опору, деформируя ее. В опоре появляется сила упругости (или сила реакции опоры), направленная вверх. В самом теле вследствие этого возникает еще одна сила упругости деформированного тела. Она приложена к опоре и направлена вниз. Эта сила и есть вес тела.

Сила тяжести по модулю равна силе упругости опоры. Но этой же силе равен и вес тела. Поэтому = mg.

Но вес тела и сила тяжести, приложенная к нему – разные силы!

Сила тяжести - это гравитационная сила, приложенная к телу. Вес тела – это сила упругости, приложенная к подвесу.

Всякое тело, на которое действует только сила тяжести или вообще сила всемирного тяготения, находится в состоянии невесомости: отсутствует вес, т.е. сила с которой тело действует на опору или подвес.

Тело каждого из нас в результате взаимодействия с опорой также деформируется. Мы воспринимаем эту деформацию, как весомость. Отсюда и произошло обыденное выражение «вес тела», хотя вес тела - это сила, приложенная не к телу, а к опоре.

Вес тела, движущегося с ускорением.

Если тело движется с ускорение, совпадающим по направлению с ускорением свободного падения (вместе с опорой или подвесом), то его вес уменьшается: P = m(g-a). Примером является движение в лифте вниз или движение автомобиля через выпуклый мост.

Если тело движется с ускорением, противоположным по направлению ускорению свободного падения (вместе с опорой или подвесом), то его вес увеличивается: P = m(g+a). Примером является движение в лифте вверх или движение автомобиля через вогнутый участок дороги.

Сила упругости.

В лабораторных условиях рассматривается поведение тел, которые под действием приложенных сил могли двигаться в любом направлении. Такие тела называются свободными. В реальных условиях перемещению тела часто препятствуют другие скрепленные или соприкасающиеся с ним тела, которые называют связью.

Тело, подвешенное на нити к потолку, не падает, так как этому препятствует связь – нить. Мостовая ферма не падает, так как этому препятствуют связи – опоры моста. Стрела подъемного крана не падает потому, что ее удерживают связи – канаты и опора.

Внешняя сила, действующая на связь или растягивает её, или сжимает, или закручивает. При этом молекулы тела, осуществляющего связь, смещаются относительно своих обычных положений. Чем больше внешняя деформирующая сила, тем больше это смещение. Но между молекулами действует силы притяжения и отталкивания, которые по третьему закону Ньютона противодействуют внешней деформирующей силе (пока деформация упругая). Это приводит к реакции связи, которая всегда имеет молекулярную природу.

По закону Гука абсолютная (упругая) деформация пропорциональна приложенной к телу силе. Следовательно, и силы упругости пропорциональны абсолютной деформации: чем больше деформация, тем больше сила упругости:

F_упр = ─ k X

Знак « ─ » показывает, что сила упругости всегда противоположна по направлению абсолютной деформации. Коэффициент «k» называют жесткостью.

Силой упругости называют силу, возникающую в теле при его деформации. Сила упругости пропорциональна абсолютной деформации и направлена противоположно деформирующей тело силе.

Сила трения.

Сила трения возникает при непосредственном соприкосновении тел и всегда направлена вдоль поверхности соприкосновения. Этим она отличается от силы упругости, направленной перпендикулярно этой поверхности.

Сила трения возникает вследствие всевозможных микроскопических неровностей поверхностей соприкасающихся тел, деформации этих неровностей и межмолекулярного притяжения в тех местах, где расстояния между частицами этих тел оказываются очень малыми.

Трение существует не только при движении тел, но и тогда, когда тела находятся в относительном покое. Например, брусок, лежащий на наклонной плоскости, не соскальзывает потому, что сила трения уравновешивает равнодействующую силу тяжести и силу реакции опоры.

Трение, возникающее между неподвижными друг относительно друга поверхностями, называют трением покоя.

Максимальная сила трения покоя зависит от материала соприкасающихся поверхностей и от силы давления N:

F_тр = N

Величину называют коэффициентом трения покоя.

Сила трения покоя препятствует началу движения, удерживает соприкасающиеся тела в относительном покое. Но иногда сила трения покоя действующая на подошву обуви, сообщает нам ускорение.

Силу трения, возникающую при движении одного тела по поверхности другого, называют силой трения скольжения. Направлена она противоположно перемещению тела относительно соприкасающегося с ним другого тела. Так же как и максимальная сила трения покоя, сила трения скольжения пропорциональна силе давления (реакции опоры) и зависит от материала соприкасающихся поверхностей:

F_тр = N

«µ» - коэффициент трения скольжения, приблизительно равен коэффициенту трения покоя . Обычно коэффициент трения меньше единицы и по модулю сила трения меньше силы давления. Смазка уменьшает силу трения примерно в десять раз (жидкое трение).

В зависимости от значения коэффициента трения скольжения, соприкасающиеся пары поверхностей делят на две группы:

фрикционные, имеющие большой коэффициент трения скольжения (до 0,6);

антифрикционные, имеющие малый коэффициент трения скольжения (до 0,15 – 0,12).

В случаях, когда надо уменьшить силу трения, скольжение трущихся поверхностей заменяют качением по ним колес, роликов или шариков. В этом случае сила трения качения. Примером служат роликовые и шариковые подшипники.

Сила трения всегда выполняет роль тормозящей силы. Именно благодаря ей, удерживается вбитый в стену гвоздь, нитки, с помощью которых пришита пуговица и т.д.

Тормозной путь (путь пройденный телом до остановки) пропорционален квадрату скорости:

=

Сопротивление, испытываемое телами при движении в жидкостях и газах.

Эксперименты показывают, что сопротивление газов и жидкостей движению зависит от скорости тела, площади поперечного сечения и от формы тела.

Сила сопротивления зависит также и от свойств среды – в воде сопротивление во много раз больше, чем в воздухе.

Сила сопротивления (сила жидкого трения) при небольших скоростях, пропорциональна скорости, а при больших скоростях она пропорциональна уже квадрату скорости.

Форму тела, при которой сила сопротивления (сила жидкого трения) мала, называют обтекаемой формой.

В жидкостях и газах нет силы трения покоя. Даже самая малая сила, приложенная к телу в жидкости или газе, сообщает ему ускорение.

Движение тела под действием силы тяжести

Тело движется по вертикали.

Еще в конце ХVI века Галилео Галилей установил, что движение свободно падающего тела – равноускоренное движение. Кроме того, ускорение свободного падения одинаково для всех тел независимо от их массы.

Законы движения, открытые Ньютоном, и закон всемирного тяготения объясняют основные особенности свободного падения.

Тело, падая, движется с ускорением по тому, что на него действует сила тяжести, направленная вниз. Ускорение постоянно, т.к. постоянна действующая на тело сила. Ускорение не зависит от массы тела по тому, что сама сила пропорциональна массе.

Ускорение падающего тела не изменится, если толкнуть тело вниз, сообщив ему начальную скорость . Только нарастание скорости тела начнется не от нуля, а от .

Если сообщить телу начальную скорость , направленную вверх, то это не изменить ни направления, ни численного значения ускорения тела, потому что толчок вверх не может изменить силу тяжести.

В обоих случаях траектория тела – вертикальная прямая.

Формулы для вычисления высот (координат) и скоростей ни чем не отличаются от формул для вычисления прямолинейного равноускоренного движения:

h = h₀ + t ± - высота;

= ± gt - скорость в. любой момент времени ;

= ± 2g (h – h₀) – скорость в любой точке траектории

(знак «+» если скорость направлена вниз, т.е совпадает по направлению с ускорением g ; «─» если скорость направлена вверх, т.е. противоположна по направлению с ускорение м g).

Начальная скорость тела направлена под углом к горизонту (тело брошено под углом к горизонту)

Часто приходится иметь дело с движениями тел, получивших начальную скорость не параллельно силе тяжести, а под некоторым углом к ней (или к горизонту). Самым ярким примером такого движения является полёт артиллерийских снарядов.

Как в этом случае летит снаряд, или копье, пущенное спортсменом, или камень, брошенный ребенком?

Вначале для простоты будем считать, что сопротивление воздуха ничтожно мало.

Если понаблюдать за движением камня или бадминтонного волана, то можно заметить, что их движение происходит по кривой весьма похожей на параболу. Эта кривая почти симметрична и можно предположить, что движение по восходящей и нисходящей ветвях продолжается одинаковое время.

Галилей отделил движение летящего снаряда по вертикали вверх и вниз от его горизонтального движения. Эксперимент подтверждает правильность такого подхода и показывает, что эти два движения не зависят одно от другого.

Подобный опыт можно проделать самому. Если бросить один камень горизонтально, а другой выпустить из рук в то же мгновение, то оба камня ударятся о пол одновременно. Камень, движущийся по кривой, чтобы достигнуть пола, должен совершить такое же перемещение по вертикали, как и камень, просто падающий вертикально. Оба камня тратят на перемещение по вертикали одинаковое время. Вообще, можно с уверенностью сказать, что оба камня в своем перемещении вниз все время находятся на одном уровне. Объяснить это можно только тем, что, как и на тело, свободно падающее, так и на тело , получившее начальную скорость, направленную вертикально, действует только сила тяжести.

Как бы тело не двигалось, сила тяжести может сообщить ему только ускорение свободного падения g. Этим определяется и траектория движения тела, и характер его движения.

Проекции вектора на оси Х и Y равны соответственно:

=

=

М

есто для формулы.

α

Основные формулы для расчета движения тела, брошенного под углом α к горизонту с начальной скоростью

Дальность полета: ℓ =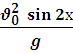

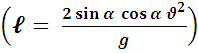
Максимальная высота подъема: h_max =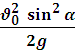

Время полета: t =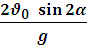

Время подъема на высоту h_max: t_n =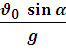

Скорость в зависимости от времени полета:

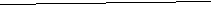
= = + -2()gt

Время падения тела брошенного под углом α к горизонту с высоты h и угол падения β:

t =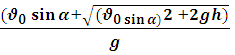

=

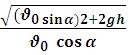
Определение времени полета до произвольной высоты h:

t² = 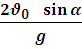∙ t + = 0

Определение расстояния от места бросания тела с высоты h^

S= ² + 2gh

Определение скорости на высоте h:

=

Уравнение движения тела , брошенного горизонтально с высоты h и скоростью на расстояние S:

h =

Максимальная дальность полета достигается при α = 45, при этом:

Искусственные спутники Земли (ИСЗ)

Тело, брошенное горизонтально со скоростью , двигаясь по параболе, пролетит в горизонтальном направлении расстояние S = t. При этом предполагается, что поверхность Земли горизонтальна. Такое предположение допустимо, если скорость бросания мала. Но в действительности Земля- шар. Поэтому одновременно с продвижением тела по его траектории поверхность Земли несколько удаляется от него.

Ньютон рассмотрел этот вопрос и пришёл к выводу, что можно подобрать такое значение скорости тела, при котором поверхность Земли из-за её кривизны будет удаляться от тела на столько, на сколько тело приближается к Земле благодаря притяжению к ней. Тогда тело будет двигаться на постоянном расстоянии h от поверхности Земли, т.е. по окружности радиусом + h, где ≈6,4∙10⁶ м- радиус Земли.

Скорость, при которой тело, брошенное горизонтально, начинает двигаться по окружности вокруг Земли, называют первой космической скоростью, а само тело будет называться искусственным спутником Земли (естественный спутник Земли - Луна).

Рассчитывая первую космическую скорость для спутника, обращающегося вокруг Земли по круговой орбите на небольшой высоте h (h). В этом случае ускорение равно ускорению свободного падения a=g, но а = , откуда = .

Подставив числовые значения, получаем:

= ≈7,9∙10³ м/с

Почти 8 километров в секунду – это около 29000 километров в час!

Движение спутников вокруг Земли происходит под действием только одной силы – силы всемирного тяготения. Эта сила сообщаем им и всем предметам, находящимся в них, одинаковое ускорение. Поэтому все тела в спутниках, в том числе и космонавты, находятся в состоянии невесомости.

Рассчитать первую космическую скорость для спутника на высоте h над поверхностью Земли можно по формул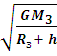е: = , где ≈6∙10²⁴кг - масса Земли.

Для того чтобы запустить ИСЗ, его с помощью ракеты-носителя выводят в верхние слои атмосферы, а затем одновременно разгоняют до первой космической скорости и поднимают до расчетной высоты.

Период обращения спутника (время, требуемое на один оборот вокруг Земли) вычисляется по формуле: T=

После того, как отработали двигатели всех ступеней ракеты, спутник движется свободно, обычно по эллиптической орбите. Чем точнее произведен запуск, тем ближе его траектория к круговой. Чем больше скорость, до которой разгоняется ракета, тем более вытянутой получается эллиптическая орбита спутника.

При скорости 11,2 км/с космический корабль преодолевает притяжение к Земле. Эта скорость называется второй космической скоростью. Именно с такой или несколько большей скоростью отправляются космические корабли, уходящие от притяжения Земли и превращающиеся в спутников Солнца.

Для того чтобы вывести ракету из сферы притяжения к Солнцу и направить ее в полет за пределы солнечной системы потребуется скорость уже в 16,7км/с (третья космическая скорость).

Законы сохранения в механике

Законы Ньютона позволят решить в принципе все задачи, связанные с взаимодействие тел. Однако часто нахождение сил взаимодействия представляет значительные трудности, а без знания сил нельзя найти ускорение, приобретаемой телами, а, следовательно, и их скорости и перемещения.

Например, с помощью законов Ньютона можно, но трудно определить силу взаимодействия ракеты и вытекающих из нее газов, силу взаимодействия тел при столкновениях и т.д.

Для решения подобных задач в механике введены специальные понятия и величины. При этом оказалось, что численные значения вновь введенных величин не изменяются в процессе взаимодействия тел. Поэтому важнейшие соотношения между сохраняющимися величинами получили название законов сохранения.

Законы сохранения – фундаментальные законы физики.

Законы сохранения являются следствием из законов движения. В них вместо сил и ускорений появляются новые величины – импульс и энергия.

Импульс.

Слово импульс происходит от латинского слова impulsus, что в буквальном переводе означает толчок.

В механике этим термином обозначают две величины: импульс сил и импульс тела.

Импульс силы.

Результат взаимодействия тел зависит не только от силы, но и от времени их взаимодействия. В этом можно убедиться проделав различные опыты, например: на лист бумаги, лежащий на столе, поставим какой-либо предмет (стакан с водой). Если медленно тянуть бумагу, то стакан сдвинется с места и будет перемещаться вместе с ней. Но если лист дернуть резко, он уйдет из- под стакана, а стакан останется на прежнем месте.

Подобные опыты свидетельствуют о том, что результат взаимодействия зависит не только от силы, но и от времени ее действия. Поэтому в физике для характеристики действия силы ввели специальную величину – импульс силы.

Импульсом силы называют векторную физическую величину, являющуюся мерой действия силы за некоторый промежуток времени.

Импульс силы измеряется произведением силы на время ее действия:

= t

За единицу импульса силы в СИ принят: Н∙с

Импульс тела или количество движения.

При проверке систем безопасности автомобилей проводят так называемые краш-тесты, при которых автомобили врезаются в препятствия. Повреждения, получаемые автомобилями и препятствиями, зависят и от скорости и от массы. Грузовик при одной и той же скорости нанесёт препятствию больший урон, чем легковой автомобиль. Но и из двух легковых автомобилей, больше повреждений нанесёт тот, который двигался с большей скоростью.

Следовательно, для характеристики взаимодействия недостаточно знать только массу тел или только их скорости. Поэтому в качестве одной из характеристик движения введена специальная величина – импульс тела или количество движения, равное произведению массы тела на его скорость:

=m

За единицу импульса тела в СИ принят килограмм-метр в секунду ().

Изменение импульса тела (количества движения) равно импульсу силы:

t = m - m

Из формулы следует, что одна и та же сила, за одно и то же время вызывает у любого тела одно и то же изменение импульса, т.к. в левую часть равенства масса не входит.

При внезапном изменении импульса тела время зачастую очень мало и его записывают в виде . Значит, можно записать

Δt = Δ(m)

Прыжки и столкновения

Попытаемся применить соотношение t = m - m для случаев, когда решаются задачи о прыжках или, например, о столкновениях автомобилей.

В данном соотношении величина F представляет собой реальную силу, которая необходима, чтобы произвести заданное изменение количества движения за указанный промежуток времени Δt. Если пол, стена или что-то ещё не развивают силы, то количество движения не изменяется.

За короткое время может произойти большое изменение импульса тела, например, когда прыгун опускается на землю или когда автомобиль врезается в стену. В этом случае ΔP велико, а Δt мало. То есть, сила F должна быть очень велика.

При столкновениях развиваются огромные силы, и, хотя они действуют в течение коротких промежутков времени, эти силы способны причинить большой ущерб. Чтобы уменьшить силу и предотвратить плачевные последствия, нужно увеличивать время Δt.

Для этого при прыжке следует сгибать ноги в коленях и надевать мягкую обувь, этой же цели служат эластичные маты. Вратари надевают особые перчатки и, задерживая мяча. Следят за тем, чтобы их рука отходила назад для увеличения промежутка времени Δt, в течение которого мяч останавливается. В автомобилях ремни и подушки безопасности также увеличивают промежуток времени Δt в течение которого скорость людей, находящихся в автомобиле, при столкновении уменьшается до нуля.

Футболист, сообщая мячу массой 0,5 кг скорость 20м/с ударом ноги, длящимся 0,01с, прикладывает к мячу силу около 1000Н! Носок бутсы должен быть очень крепким.

Борец, когда его бросают на ковер, пытается по возможности удлинить время «приземления», расслабив мышцы и распределяя удар об пол на ряд последовательных столкновений, в которых участвовали бы лодыжки, колени, ребра, плечи.

Немного истории.

Понятие импульса было введено Рене Декартом в первой половине ХVII века. Из-за отсутствия в то время физического понятия массы, он определял импульс, как произведение «величины тела на скорость его движения» . Это произведение Декарта выражало «количество движения» и появилось в его трудах при исследовании столкновений тел.

Определение импульса, данное Декартом, было уточнено Ньютоном. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».

В формулировке Декарта (1639 г.) закон сохранения импульса звучал так: «Во вселенной, во всей созданной материи есть известное количество движения, которое никогда не увеличивается, не уменьшается, и, таким образом, если одно тело приводит в движение другое, то теряет столько своего движения, сколько его сообщает». Отсутствие понимания о векторном характере закона не позволило Декарту создать правильную теорию столкновения тел.

Закон сохранения импульса (количества движения).

Импульс обладает интересным и важным свойством, которое есть лишь у немногих физических величин. Это свойство сохранения.

В чем оно состоит?

Свойство сохраняться - это свойство оставаться неизменным. Именно таково свойство импульса тел. Относится оно к случаю, когда два или более тел взаимодействуют друг с другом, но на них не действуют внешние силы. Такая группа тел, или, как говорят, система тел называется замкнутой: замкнутая система тел – это совокупность тел, взаимодействующих между собой, но не взаимодействующих с другими телами.

При столкновениях тел происходит обмен количеством движения, перераспределение количества движения между телами. Все реальные опыты показывают, что количество движения не приобретается, не теряется, а происходит лишь обмен количеством движения или перераспределение его между телами.

Этот вывод не зависит от рода столкновения. Идет ли речь о легком упругом соударении, столкновении, при котором тела «склеиваются» друг с другом или о страшном столкновении, сопровождающимся превращением огромных количеств кинетической энергии в теплоту, - все равно количество движения сохраняется. Это дает нам важный принцип: приобретенное количество движений = потеря количества движения, или в другой форме: суммарное количество движения ни когда не меняется.

Если взаимодействуют не два, а много тел то и в этом случае сумма количества движения замкнутой системы не изменяется (сохраняется).

В этом и состоит закон сохранения импульса (количества движения): геометрическая сумма импульсов тел (количеств движения), входящих в замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.

Таким образом, импульс тела (количество движения) или системы тел может изменяться только под действием внешних сил. Именно поэтому барон Мюнхгаузен не мог вытащить себя за волосы из болота.

Закон сохранения импульса выполняется в любой инерциальной системе отсчета.

Так как импульс тела никогда не теряется и не создается вновь, а происходит лишь обмен между телами, то можно сделать вывод, что два тела, которые сталкиваются между собой, должны действовать друг на друга с равными и противоположно направленными силами, т.е. выполняется третий закон Ньютона: действие равно противодействию.

Закон сохранения импульса не является следствием законов Ньютона. Это фундаментальный, самостоятельный закон природы, не знающий никаких исключений. Этот закон абсолютно точно соблюдается и в микромире и в макромире.

Формула закона сохранения импульса в общем случае для двух взаимодействующих тел записывается так:

m₁ + m₁ = m₁ + m₂ (для абсолютно упругого удара);

m₁ + m₁ = (m₁ + m₂) (для абсолютно неупругого удара).

Абсолютно упругий и неупругий удары.

Ударом называется столкновение тел, при котором за весьма малый промежуток времени происходит значительное изменения скоростей тел.

Удар называют абсолютно неупругим, если тела после столкновения образуют одно новое тело. Примером такого удара может служить столкновение двух кусков пластилина, которые сливаются и образуют новый кусок, или столкновения пули с мешком, наполненным песком (пуля после удара застревает в песке).

При неупругом ударе кинетическая энергия тела, образовавшегося в результате взаимодействия, не равна сумме кинетических энергий, которыми исходные тела обладали до удара. Часть механической энергии превращается во внутреннюю энергию – тело деформируется и нагревается.

Абсолютно упругим называют такой удар, в ходе которого, не происходит необратимых преобразований кинетической энергии во внутреннюю энергию.

После абсолютно упругого удара сохраняется и импульс, и кинетическая энергия системы тел.

Очень близки к упругим ударам столкновения стальных шаров.

При абсолютно упругом косом ударе гладкого шара о стенку (m_c >> m _ш и ), шар отскакивает от стенки по закону зеркального отражения: угол отражения равен углу падения. Численное значение скорости шара сохраняется. Вектор изменения импульса шара при ударе направлен перпендикулярно к стенке. Импульс ударной силы, действующей на стенку равен 2 m_ш.

Понятие о реактивном движении.

Представим себе тихое, спокойное озеро, на поверхности которого покоится лодка, нагруженная одинаковыми камнями. На груде камней стоит человек. Лодку, человека и камни можно рассматривать как замкнутую систему тел, т.к. их взаимодействие с окружающей средой пренебрежимо мало. Рассмотрим, что произойдёт, если человек начнёт бросать камни один за другим в горизонтальном направлении через одинаковые промежутки времени с одинаковой относительно лодки скоростью .

Бросив первый камень массой m, человек сообщит ему импульс m. Но и сама лодка с человеком и камнями получит такой же импульс по величине, но противоположный по направлению. Скорость лодки относительно берега можно определить из равенства:

= ─ , где М- масса лодки, человека и камней.

После второго броска скорость лодки возрастёт на Δ, после третьего - ещё на Δ и т.д.(Δ, Δ - не равны, т.к. уменьшается общая масса лодки, человека и камней из-за выбрасывания последних).

Следовательно, с каждым броском камня скорость лодки будет возрастать (но не бесконечно, т.к. возрастает сила сопротивления движению).

Такое движение, возникающее при отталкивании тел замкнутой системы друг от друга, называется реактивным.

Реактивное движение мы часто наблюдаем в повседневной жизни:

Водопроводный кран («гусак») отклоняется в противоположном направлении струе вытекающей воды;

Свёрнутый шланг для полива, начинает развертываться при пуске воды. Его заставляет развертываться реактивная сила водяной струи.

Человек научился использовать реактивное движение в своих интересах и создал реактивные двигатели, используемые на самолетах и в ракетах. Рассмотрим принцип работы ракеты. В простейшем случае ракета состоит из корпуса, который одновременно является и топливным баком, т.е. хранилищем вещества, которое выбрасывается из корпуса.

Ракета – удивительное изобретение. Автомобилю для его движения нужна дорога, самолету для полета нужен воздух, отталкиваясь от которых они могут двигаться. Ракета движется, не взаимодействуя с другbми телами. Она взаимодействует с теми газами, которые образуются при сгорании топлива. Скорость ракеты вычисляется по формуле: = - ,

где m – масса газов, вытекающих их ракеты, - его скорость, М – масса ракеты.

Формула подсказывает два способа увеличения скорости ракеты – 1) увеличивая отношение m/ М; 2). увеличивая скорость выброса вещества.

В настоящее время широко используются термохимические ракетные двигатели, в которых при сжигании топлива образуются сильно нагретые и сжатые газы, истекающие с большой скоростью через сопло.

Энергия. Закон превращения и сохранения энергии.

В процессе взаимодействия тел одни формы движения могут превращаться в другие. Например, при механическом движении тела его движение превращается во внутреннее движение молекул тел (они нагреваются). На гидроэлектростанциях механическое движение воды превращается в движение электронов в проводнике.

Мерой механического движения является импульс тела (количество движения). Однако, импульс тела не может быть количественной мерой других видов движения, так как при образовании механического движения в другие виды, импульс тела уменьшается и даже может стать равным нулю.

Поэтому была введена специальная физическая величина – энергия (от греческого слова energia - деятельность).

Энергия – это физическая величина, с помощью которой можно количественно охарактеризовать любой движение. Иными словами, энергией является универсальной количественной мерой движения.

Для анализа качественно различных форм движения в физике введены различные виды энергии: механическая, внутренняя, электромагнитная, ядерная и т.д.

Понятие об энергии первоначально выработалось в механике. В 1686 г. немецкий философ и ученый Готфрид Вильгельм Лейбниц предлагает ввести понятие «живой силы» - половине произведения массы на квадрат скорости, т.е. в современном обозначении – кинетической энергии. следует помнить, что Лейбниц называл «живой силой» не , а . Разделить ее на 2 предложил в 1829 году французский механик Гюстав Гаспар Кориолис на основании теоремы, оказанной за несколько лет до этого французским математиком Лазаром Никола Карно – 2F = - m _.

Энергия – это только одна из характеристик движения и не существует сама по себе отдельно от взаимодействующих тел, частиц и их движения. Нельзя дать энергии четкого определения. «Почувствовать» ее можно после знакомства и рассуждений о работе, о теплоте, выделяющейся при сгорании топлива, о превращениях энергии – переходах ее из одной формы в другую. Чтобы лучше понять, что такое энергия нужно перейти к другому ее «официальному» определению: энергия – это способность совершать работу.

Энергия является фундаментальным понятием физики.

Что же такое «работа»?

Работа.

В результате взаимодействия энергия тел может изменяться. Для характеристики изменения энергии взаимодействующих тел была введена специальная физическая величина – работа силы.

В теореме доказанной Лазаром Карно 2F = - m произведение силы на перемещение и соs угла между ними Кориолис вслед за другим французским механиком, Жаном Виктором Понселе (1788-1867), назвал работой. Если обозначить ее буквой А и записать А=FS , то теорему можно переписать в следующем виде: А = - .

Появившиеся в знаменателях «2» дали основание Кориолису принять за меру движения половину лейбницевской «живой силы». Единицей измерения энергии и работы в СИ является джоуль (Дж).

Работа постоянной силы равна произведению модуля вектора силы на модуль вектора перемещения и на косинус угла между этими векторами: А=FS.

Если направление силы и перемещения совпадают, то А=FS.

Выражение А = - , принято называть теоремой о кинетической энергии.

В соответствии с ней работа сил, действующих на тело (или на систему тел), равна изменению кинетической энергии этого тела.

Из теоремы следует, что кинетическая энергия равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему заданную скорость движения.

Поскольку скорость – величина относительная, то относительной является и кинетическая энергия.

Следующий важный шаг в развитии понятия энергии был сделан в 1847 году немецким ученым Германом Людвигом Фердинандом Гельмгольцем (1821-1894). Изучая движение тел под действием сил, которые постоянны или зависят от расстояния, но не от времени и скорости, он обратил внимание на то, что левую часть уравнения А = - в таком случае всегда можно представить в виде разности значений некоторой величины, характеризующей взаимодействие рассматриваемых тел. Поскольку новая величина имела такую же размерность, что и «живая сила», Гельмгольц предложил и ее назвать «силой», только не «живой», а «напряженной». Впоследствии она была переименована в потенциальную энергию.

Потенциальная энергия – это энергия взаимодействия. Она определяется работой, которую должны совершить силы, чтобы переместить тело из данного положения в нулевое (то, в котором потенциальная энергия считается равной нулю). Выбор нулевого положения произволен.

Поэтому потенциальная энергия определена не однозначно: по отношению к разным нулевым уровням, потенциальная энергия одного и того же тела будет различной.

Например, потенциальная энергия тела взаимодействующего с Землей может быть найдена по формуле: E = mgh, где h – высота центра тяжести тела, отсчитываемая от нулевого уровня. Принимая за нулевой уровень поверхность Земли, пола в комнате или стола, над которым находится тела, мы получим разные значения h и соответственно разные значения потенциальной энергии.

Для потенциальной энергии справедлива теорема о потенциальной энергии: работа консервативных сил равна изменению потенциальной энергии, взятому с обратным знаком.

Еще кое-что о силах, энергии и работе.

Силы, препятствующие движению, совершают отрицательную работу (сила тяжести при подъеме тела вверх, силы трения и т.д.).

Силы, работа которых не зависит от формы пути, называют консервативными (т.е. не воспринимающими изменения формы пути).

Силы, работа которых зависит от формы пути, называют неконсервативными (например, сила трения).

Когда сила, действующая на тело, направлена в сторону движения, кинетическая энергия увеличивается – сила совершает положительную работу. Если сила направлена в сторону противоположную направлению движения тела, она совершаем отрицательную работу и кинетическая энергия тела уменьшается.

Вообще, во всех случаях работа силы равна изменению энергии тела А = ±, т.е. работа, как и энергия, - это скалярная величина, являющаяся мерой превращения одного вида энергии в другой.

Если сила не постоянна, для расчета работы необходимо найти среднее значение силы на данном перемещении.

Закон сохранения механической энергии.

Рассматривая консервативные системы, в которых существуют лишь консервативные силы (наряду с силами вообще не совершающими никакой работы), Гельмгольц пришел к выводу, что работа может быть выражена и через приращение кинетической энергии системы, и через убыть ее потенциальной энергии. Это означает, что всякое увеличение кинетической энергии рассматриваемой системы всегда сопровождается соответствующим уменьшением ее потенциальной энергии и наоборот. Следовательно сумма кинетической о потенциальной энергии рассматриваемой системы в процессе ее движения не меняется (сохраняется). На основании этого обе энергии можно объединить в одну – полную механическую энергию системы.

При любых процессах, происходящих в консервативной системе, ее полная механическая энергия остается неизменной. Это утверждение называется «законом сохранения механической энергии».

Закон сохранения механической энергии выполняется при работе сил тяжести и упругости, но не выполняется при работе сил трения.

Чем отличается работа силы трения от работы других сил? Сила трения всегда направлена против направления движения. В этом ее главное отличие от сил тяжести и упругости. Работа сила тяжести и силы упругости может быть и положительная и отрицательная. Работа силы трения – всегда отрицательная.

В случае движения тела под действием силы трения кинетическая энергия тела уменьшается, но обратного пути превращения в потенциальную у неё нет (как, например, у тела, брошенного вверх).

Таким образом, когда на тело действует сила трения (сама по себе или вместе с другими силами), закон сохранения полной механической энергии нарушается – она уменьшается.

Причина в том, что трение одного тела о другое всегда приводит к нагреванию обоих трущихся тел, т.е. кинетическая энергия движущихся тел переходит в кинетическую энергию молекул, из которых состоят все тела. Следовательно, механическая энергия превращается во внутреннюю и закон сохранения полной энергии выполняется, если под полной энергией понимать не только механическую энергию, а сумму всех видов энергии.

Опыт показывает, что механическое движение никогда не исчезает бесследно и никогда не возникает само собой. Например, во время торможения автомобиля происходит нагревание тормозных колодок, шин автомобиля и асфальта.

При любых физических взаимодействия энергия не возникает и не исчезает, только превращается из одной формы в другую.

Этот экспериментально установленный факт называется – законом сохранения и превращения энергии.

Мощность.

В любой машине, в любом механизме происходит преобразование одного вида энергии в другой, т.е. совершается работа. Но в понятии работы время не играет никакой роли.

Но в технике важно, какое время необходимо затратить на совершение определенной работы. Сведения об этом дает мощность.

Мощность показывает, насколько быстро машина передает (или может передать) энергию.

Например, здоровый человек каждую секунду переводит из химической энергии в механическую около 0,7 Дж энергии, полученной в виде пищи, когда он поднимает грузы. Такая способность может поддерживаться в течение нескольких часов. Если же он попробует работать в десять раз быстрее, т.е. ежесекундно будет превращать из химической формы в механическую 7 Дж энергии, то сможет работать так не более нескольких минут.

Вообще, каждая машина имеет предел скорости с которой она может превращать энергию: например, электромоторы, мало потребляющие энергии на холостом ходу, очень эффективны при средней нагрузке и останавливаются с воем при перегрузке.

Таким образом, мощность можно определять как:

• Скорость передачи энергии

• Скорость совершения работы

• Количество работы в единицу времени

• Отношение работы к отрезку времени, в течение которого она совершена: N = =

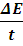Мощность, развиваемая двигателем равна:

N = = = F = F

За единицу мощности в СИ принят ватт (Вт).

Здоровый мужчина, взбегая по лестнице, может в течение нескольких секунд превращать химическую энергию в потенциальную со скоростью 1кВт!

Измерения показали, что сильная лошадь, везущая груз, может развивать мощность около 746 Вт. Это стало основой технической единицы мощности «лошадиная сила» (в оригинале «лошадиная мощность» - «horse power»). Ввел эту единицу мощности Джеймс Уатт (1736-1819), в честь которого и названа современная единица мощности – ватт. Именно Уатту обязан прогресс создания паровых машин. Он работал в те времена, когда лошади приводили в движение, практически, все механизмы (может быть только за исключением водяных и ветряных мельниц, кораблей – парусников). Предприимчивый Уатт наладил производство паровых машин, в которых использовал изобретенный им, универсальный паровой двигатель непрерывного действия. Когда приходили заказчики, они, как предусмотрительные люди, задавали вопрос: «Если я куплю одну из ваших машин, то сколько она заменит лошадей?» Вот почему и назвал Уатт единицу мощности «лошадиной». В русском языке слово «сила» появилась из-за неправильного перевода английского слова «power».

Следует помнить, что лошадиная сила, применяемая в странах СНГ равна 735,499 Вт, в отличие от британской (европейской), равной 745,7Вт.

Коэффициент полезного действия (КПД).

При работе всех машин всегда строго выполняется закон сохранения и превращения энергии: ни в одной машине, ни в одном двигателе нельзя получить энергии больше, чем затрачено.

Наоборот, в любой машине часть энергии бесполезно превращается во внутреннюю энергию (тепло), которая рассеивается в пространство.

Та часть затраченной энергии, которая преобразуется в нужный нам вид энергии, называется полезной.

Для характеристики эффективности использования энергии машинами введена специальная величина – коэффициент полезного действия (КПД), который равен отношению полезной работы (преобразованной энергии) ко всей совершенной (полной) работе (затраченной энергии):

= ∙ 100%

КПД всегда меньше 1 (меньше100%), так как в любой устройстве действуют силы трения.

КПД машины можно вычислить, как отношение полезной мощности на выходе к полной мощности на входе:

= ∙ 100%