Презентация "План работы:" – проект, доклад
Презентацию на тему "План работы:" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 42 слайд(ов).
Слайды презентации
Список похожих презентаций
План работы методического объединения учителей-логопедов ДОУ Центрального округа на 2013-2014 учебный год
Методическая тема. Актуальные проблемы коррекционно-развивающего обучения в аспекте новых образовательных стандартов. Цель: содействие профессиональному ...Планирование работы с персоналом организации
1. Понятие кадрового планирования в HR-менеджменте. Кадровое планирование — функция процесса управления персоналом, направленная на определение потребности ...Планирование воспитательной работы
Под планированием воспитательной работы в классе принято понимать процесс совместной деятельности классного руководителя, детей и взрослых по определению ...Мотивационное планирование работы
1. Понятие «мотивации». Мотив: побуждает человека к действию, определяет, что надо сделать, определяет, как будет осуществлено это действие. Мотивация ...Защита курсовой работы
Доклад по работе Презентация Ответы на вопросы по работе. Презентация - это визуальное представление курсовой, проекта, диплома, чаще с помощью программ ...Оценка и аттестация персонала. Управление результативностью работы персонала.
Эффективность. соответствие того, что делает работник, целям организации и установленным требованиям; выполнение работы наиболее рациональными и экономичными ...Особенности работы с родителями детей инвалидов
Личностно-ориентированный подход в воспитании ребенка. Развитие всех потенциальных возможностей ребенка: психических, физических, интеллектуальных, ...Шаблон презентации проектной работы
Краткое описание проекта (на 20 секунд!). Проект_________(название), который помогает решать _________(целевая аудитория) проблему ___________(описание ...Шаблон матриц курсовой работы
Постановка целей. Дерево целей. Пример целей и задач маркетинговой деятельности. Бюджет = …руб. . Краткий план анализа рынка. . . Незаменимые советов ...Способы поиска работы
Что ж давайте разберем – А что же такое РАБОТА? Работа – это обмен вашего времени, знаний, навыков и умений на материальные и нематериальные блага, ...Медицинские аспекты и организационные формы работы врача в ДОУ
ФУНКЦИОНАЛЬНЫЕ ОБЯЗАННОСТИ ВРАЧА ДДУ. 1.Врач должен систематически повышать свою квалификацию в области физиологии, психологии и патологии детей дошкольного ...Математический пакет mathcad. Основы работы с системой mathcad
Математические пакеты. Начиная с 90-х годов прошлого века, широкую известность приобрели так называемые системы компьютерной математики или математические ...Лекция 2.Информационные технологии работы с базами данных
Учебные вопросы. Основные понятия баз данных Реляционный подход к построению инфологической модели Построение инфологической модели Функциональные ...Компоненты исследовательской работы
Алгоритм исследования Определение проблемы, темы, объекта и предмета исследования Анализ степени изученности проблемы в науке и практике Определение ...Каменные работы
. материалы искусственные природные. кирпич и камни керамические и силикатные; кирпич пустотелый и полнотелый массой не более 4,3 кг; камни бетонные ...Интерактивные формы работы с родителями
Понятие «интерактивный» происходит от английского «interact» (« inter» — «взаимный», «act» — «действовать»). Смысл понятий. Цели интерактивных форм ...Измерительные работы на местности
Задание: определить высоту объекта. Ход работы: Сфотографировать объект Измерить часть объекта Измерить туже часть объекта на фото Составить пропорцию ...План занятия
План занятия. Резьбонарезные станки Резьбофрезерные станки Станки строгально-протяжной группы Продольные одностоечные станки Продольные двухстоечные ...План розвитку Великобудищанської спеціалізованої школи І-ІІІ ступенів
І. Паспорт Плану розвитку ІІ. Вступ ІІІ. Аналіз навчально-виховного процесу і матеріально-технічної бази ІV. Концептуальні засади V. Плановий комплекс ...Методы и теории социальной работы с молодежью
Молодежь – одна из самых существенных групп общества, которая всегда находится в деятельности всей социальной жизни общества. Без молодежи невозможно ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:4 июня 2019
Категория:Разные
Содержит:42 слайд(ов)
Поделись с друзьями:
Скачать презентацию



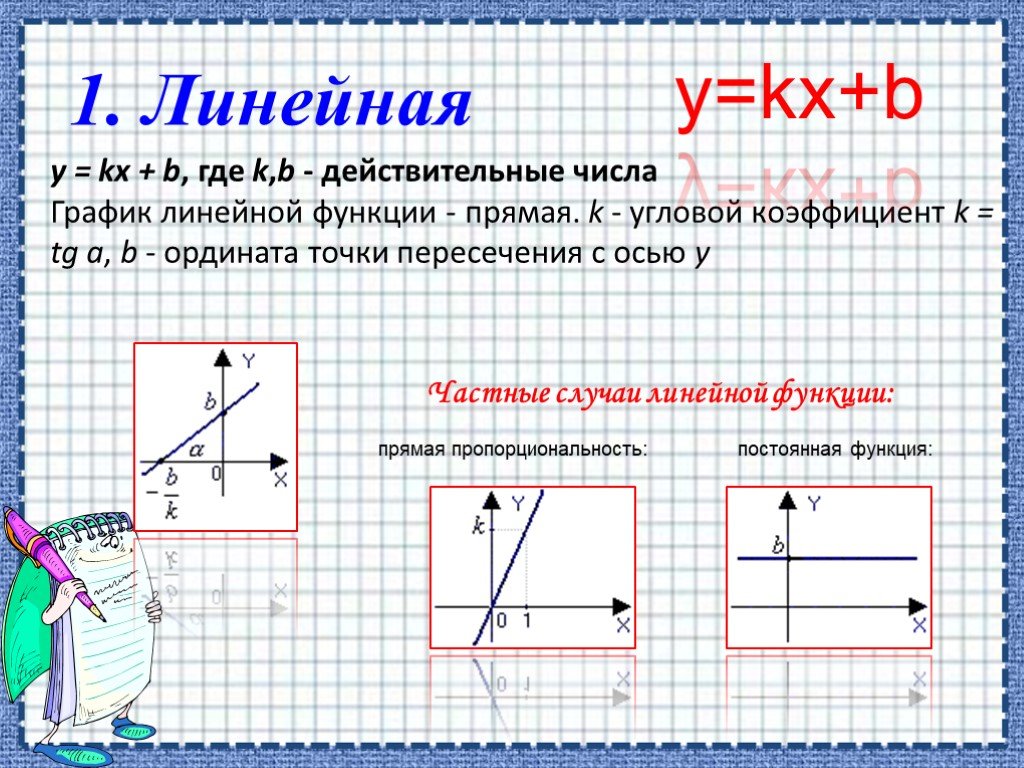

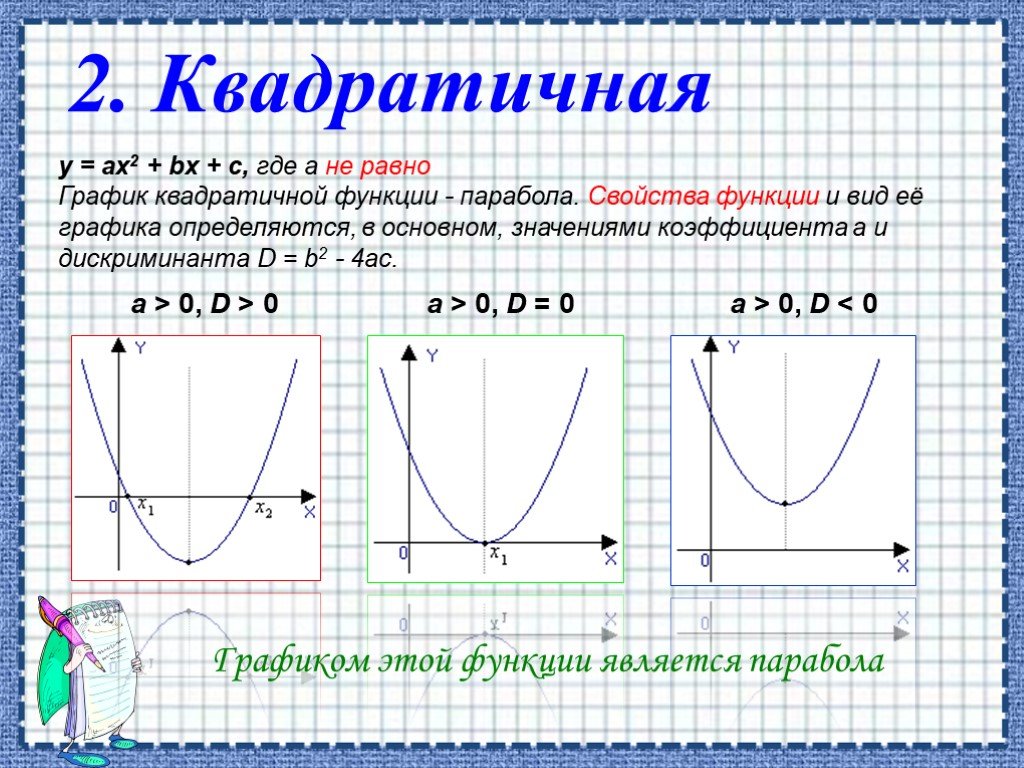
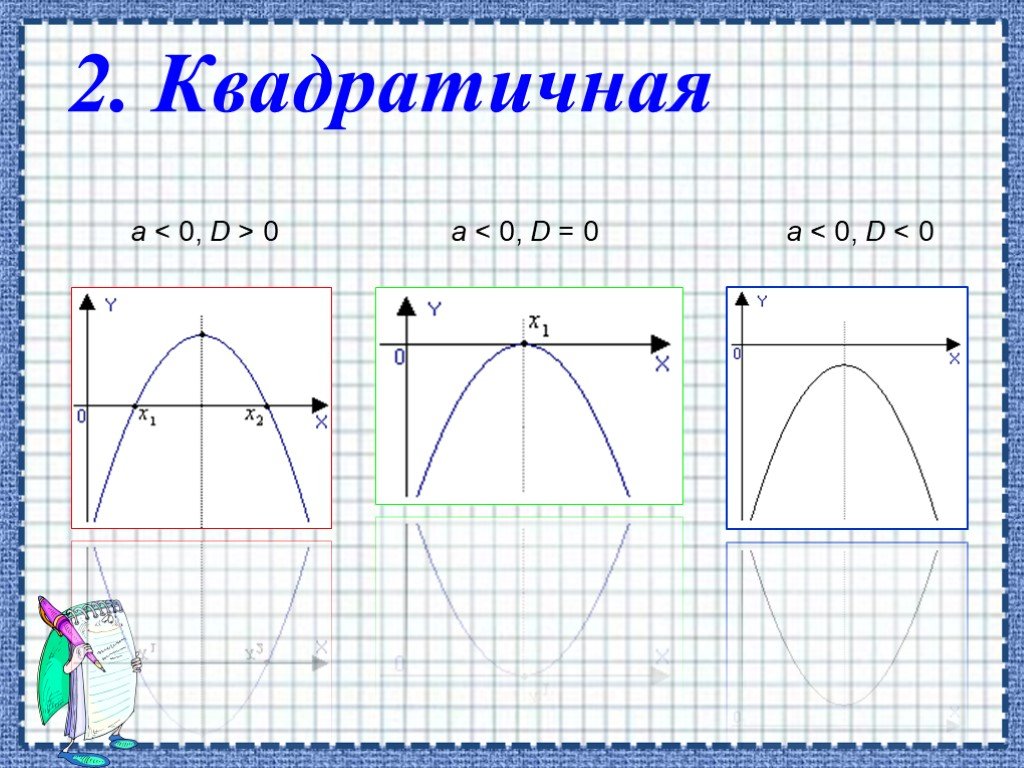



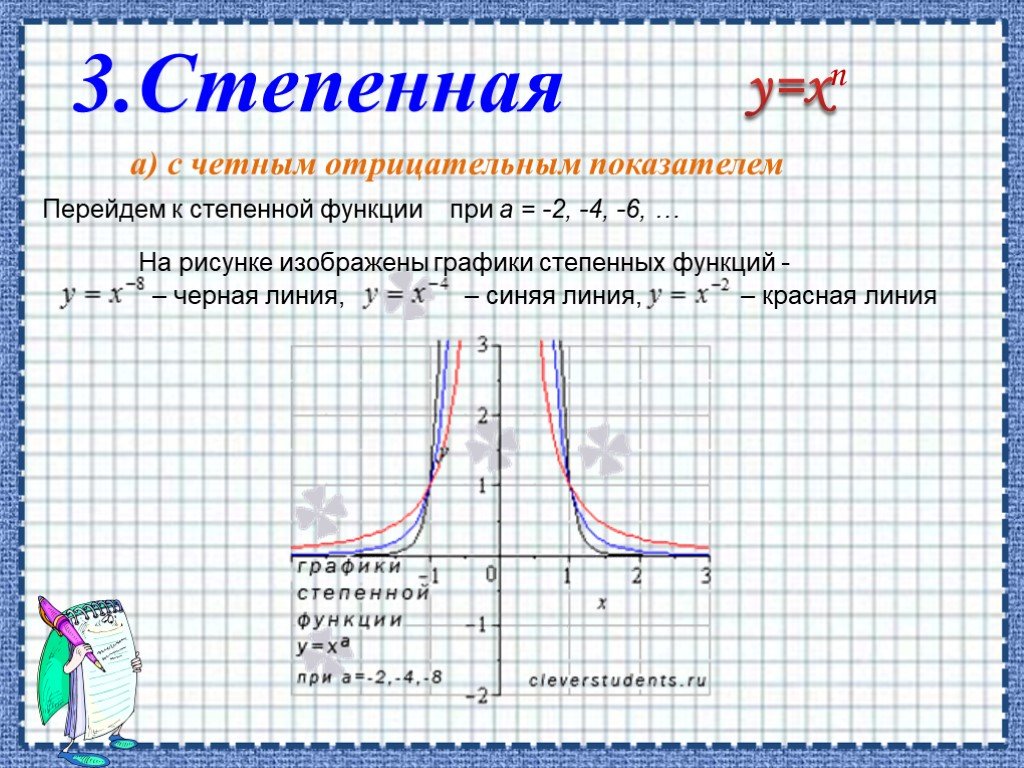

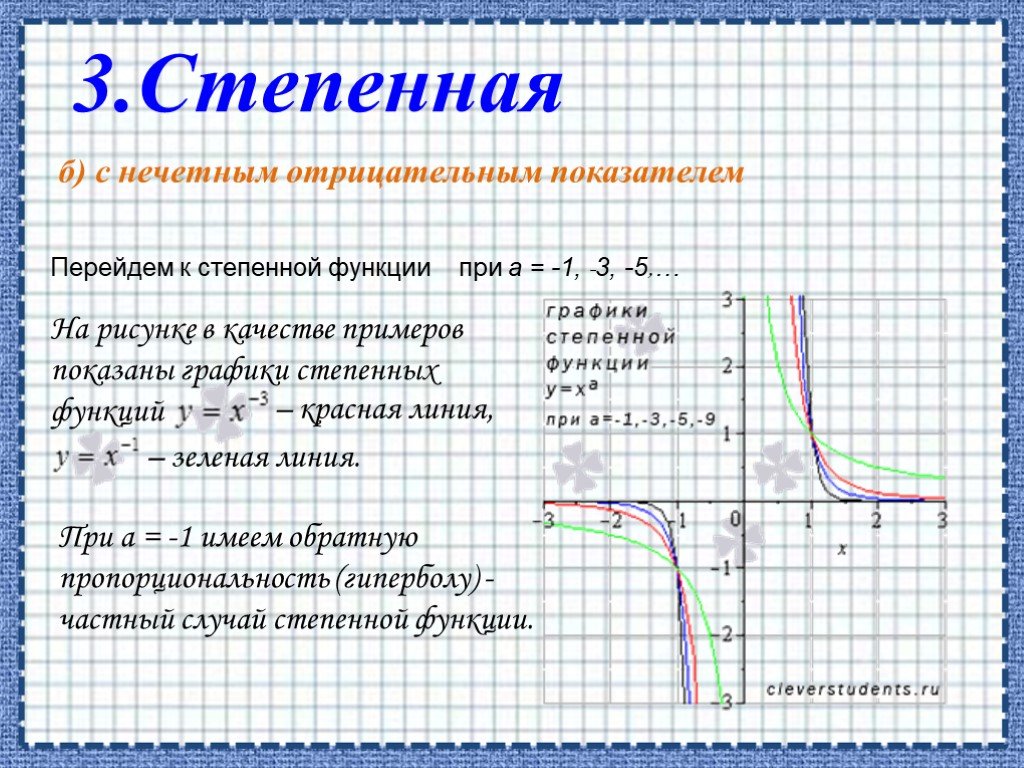


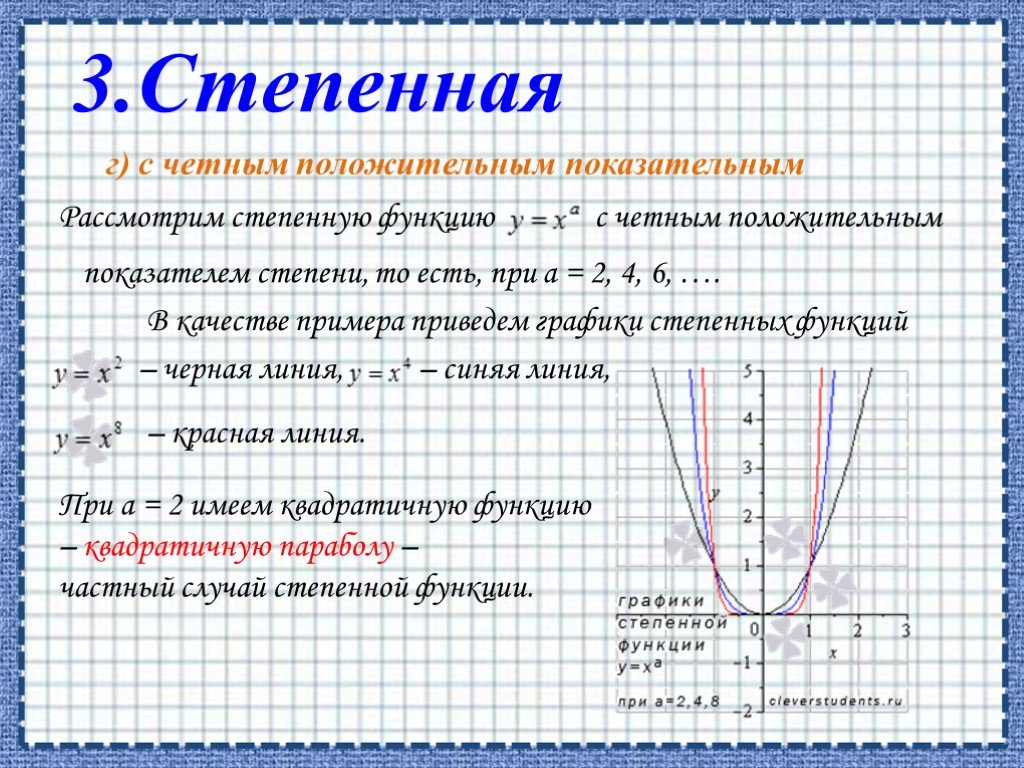
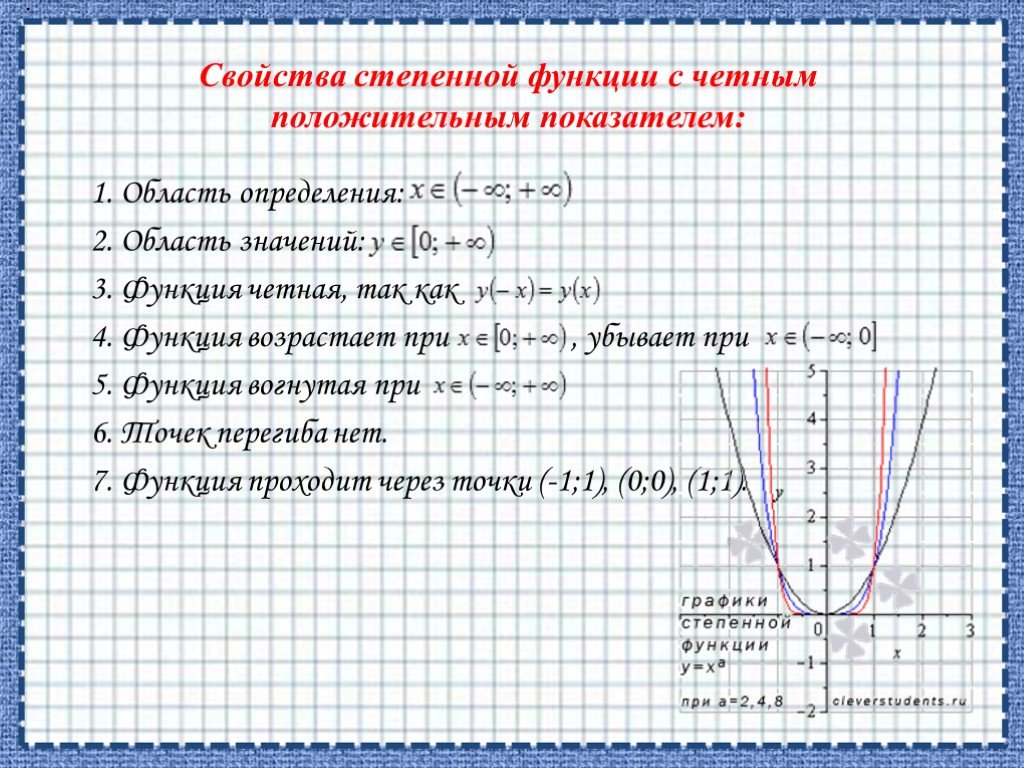

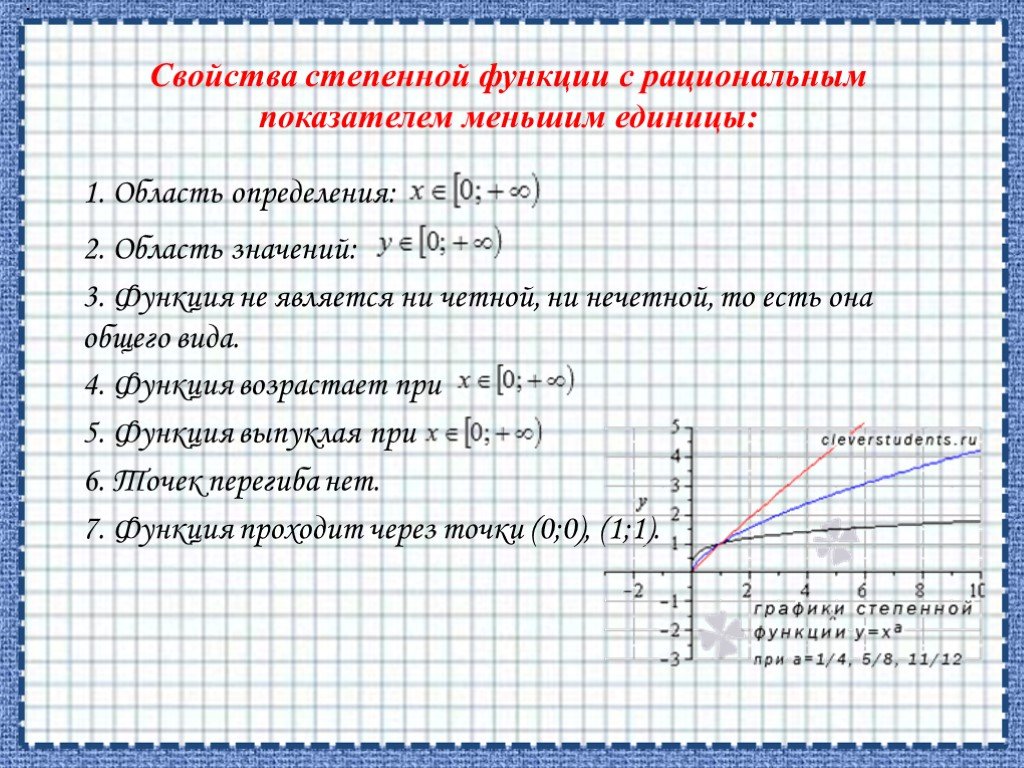
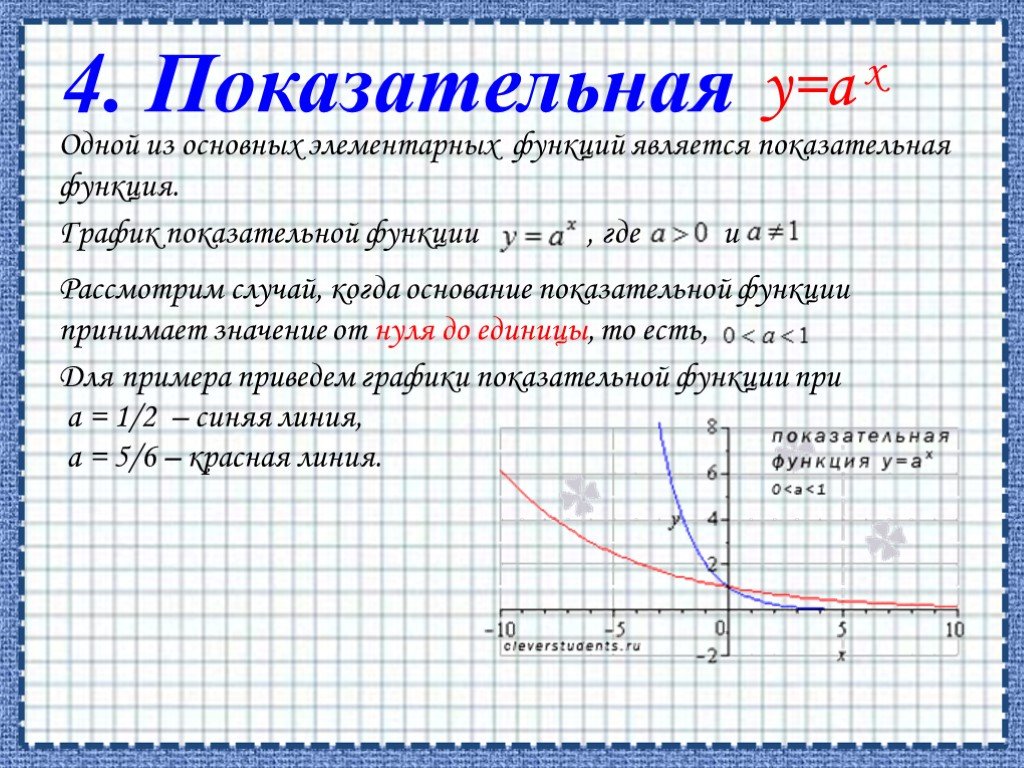



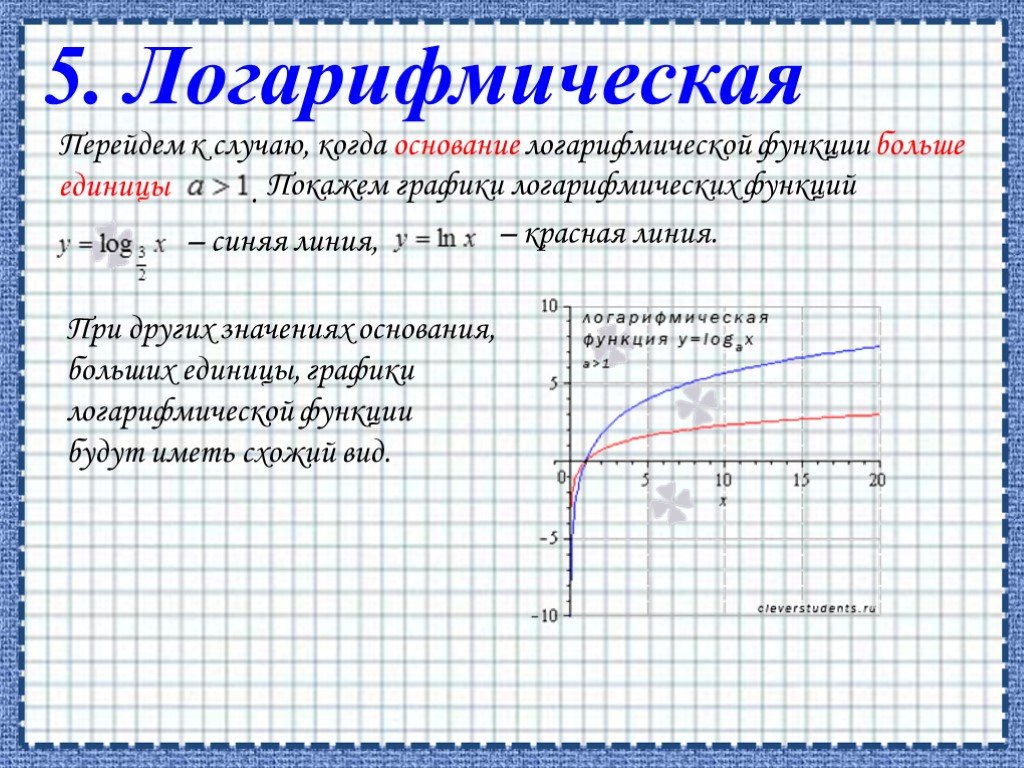
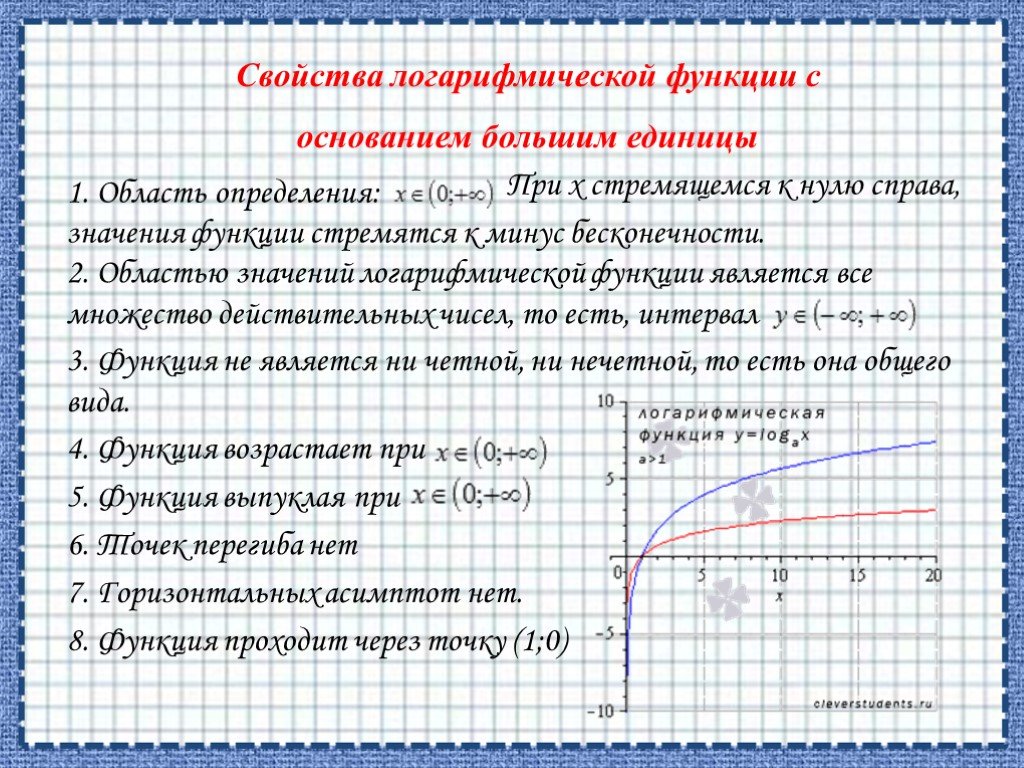

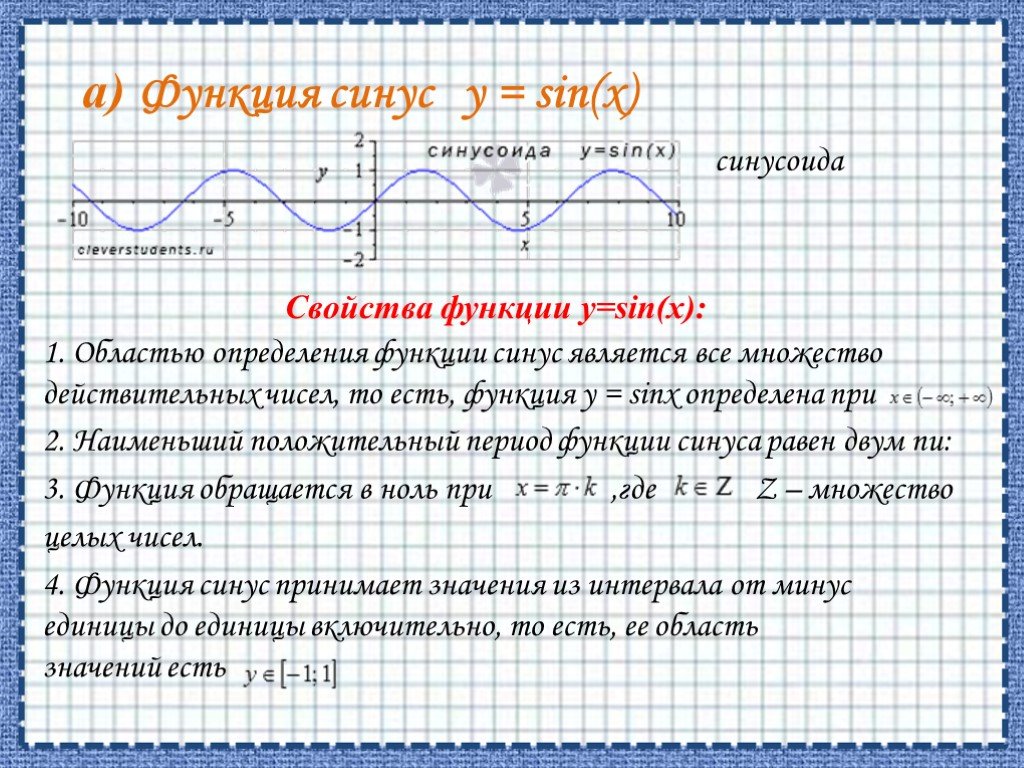



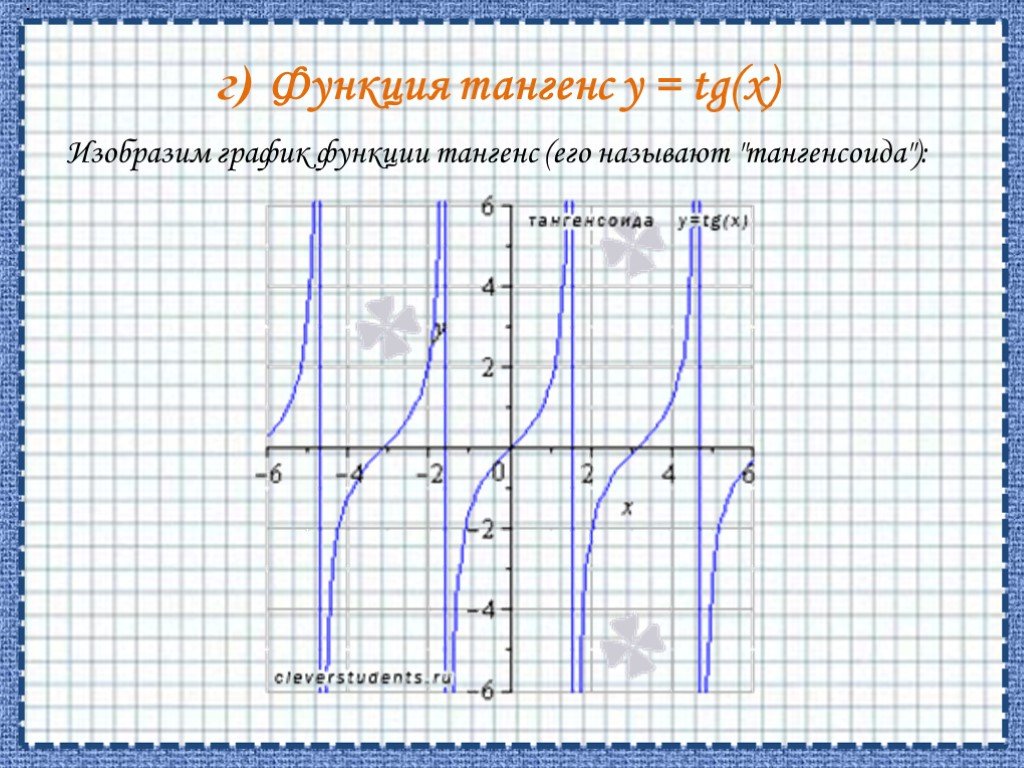

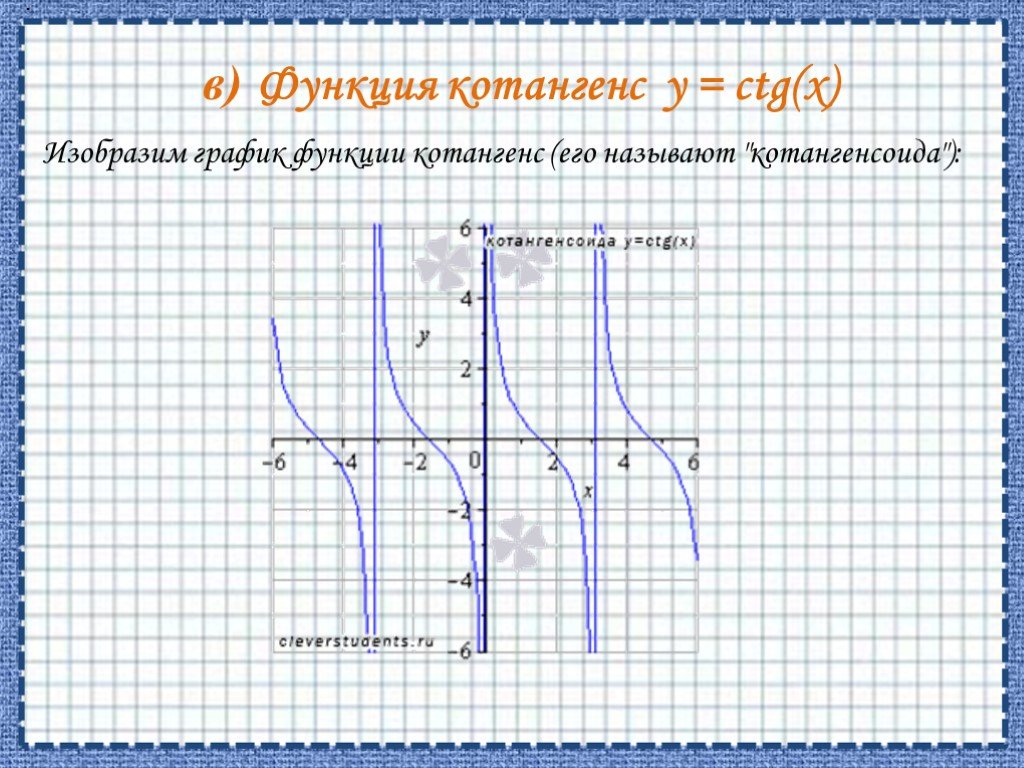

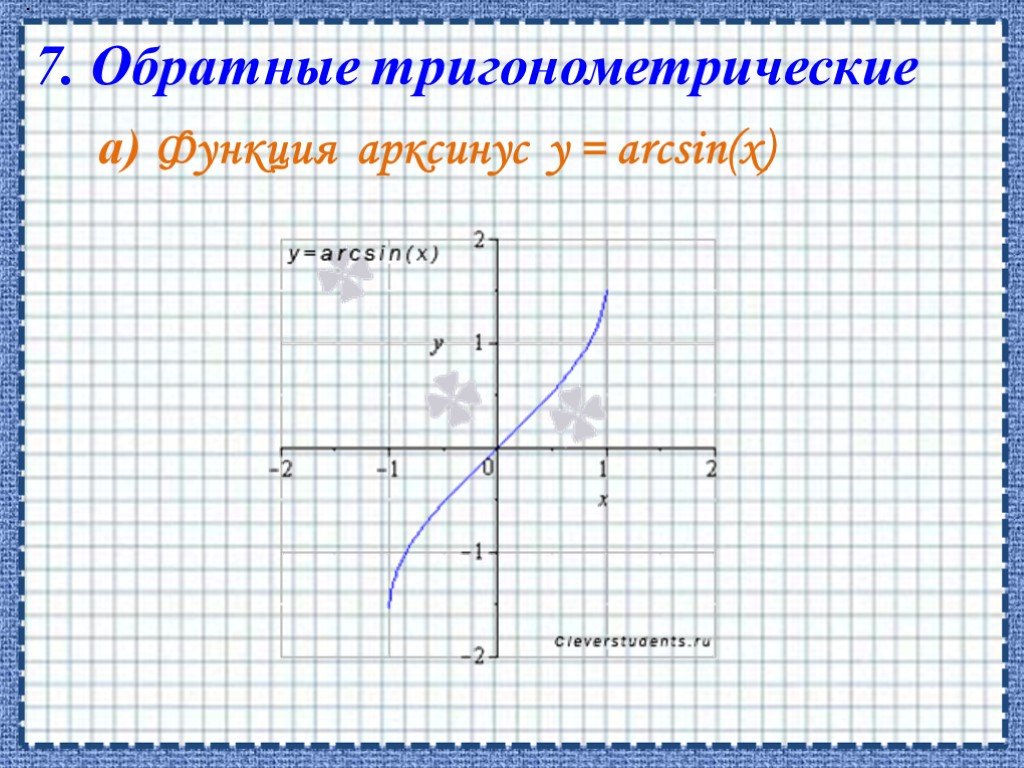

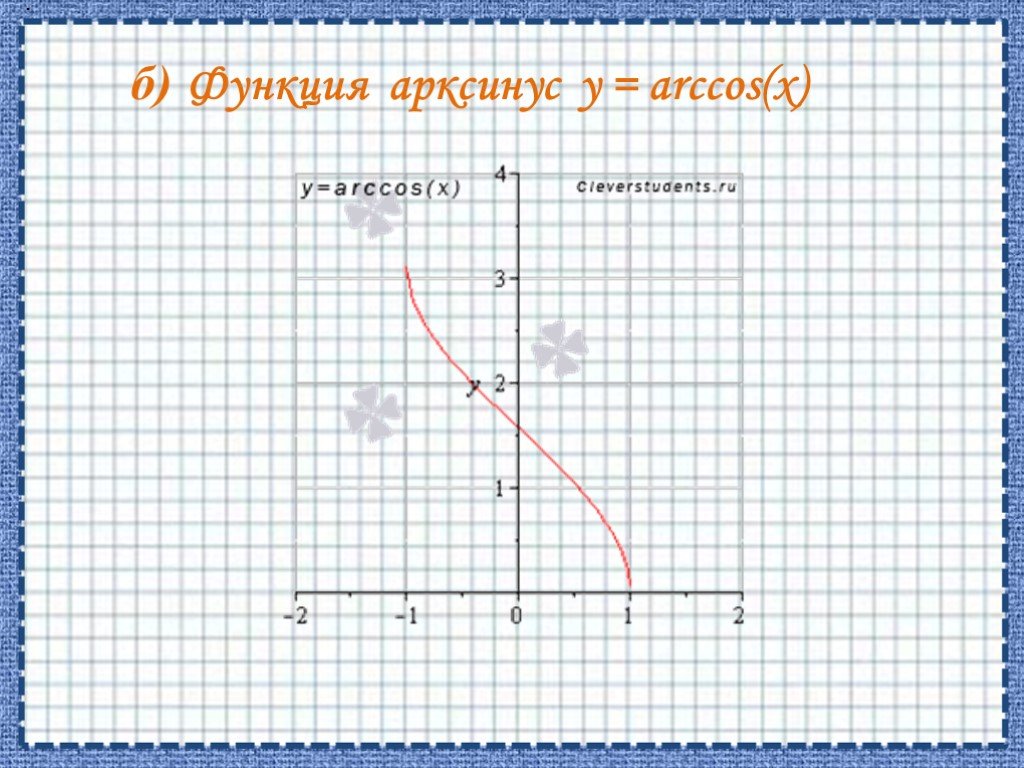









![ОБЛАСТЬ ОПРЕДЕЛЕНИЯ: R. ОБЛАСТЬ ЗНАЧЕНИЙ: ЧЕТНОСТЬ, НЕЧЕТНОСТЬ: НУЛИ: при а > 0 [-D/(4a); ∞) при а < 0 (-∞; -D/(4a)]. при b = 0 функция четная при b ≠ 0 функция не является ни четной, ни нечетной. при D > 0 два нуля: при D = 0 один нуль функции: при D < 0 нулей функции нет. Свойства квад ОБЛАСТЬ ОПРЕДЕЛЕНИЯ: R. ОБЛАСТЬ ЗНАЧЕНИЙ: ЧЕТНОСТЬ, НЕЧЕТНОСТЬ: НУЛИ: при а > 0 [-D/(4a); ∞) при а < 0 (-∞; -D/(4a)]. при b = 0 функция четная при b ≠ 0 функция не является ни четной, ни нечетной. при D > 0 два нуля: при D = 0 один нуль функции: при D < 0 нулей функции нет. Свойства квад](https://prezentacii.org/upload/cloud/19/06/151381/images/thumbs/screen7.jpg)
































































