Презентация "Координаты вектора." (9 класс) по математике – проект, доклад
Презентацию на тему "Координаты вектора." (9 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Разложение вектора по двум неколлинеарным векторам. Координаты вектора
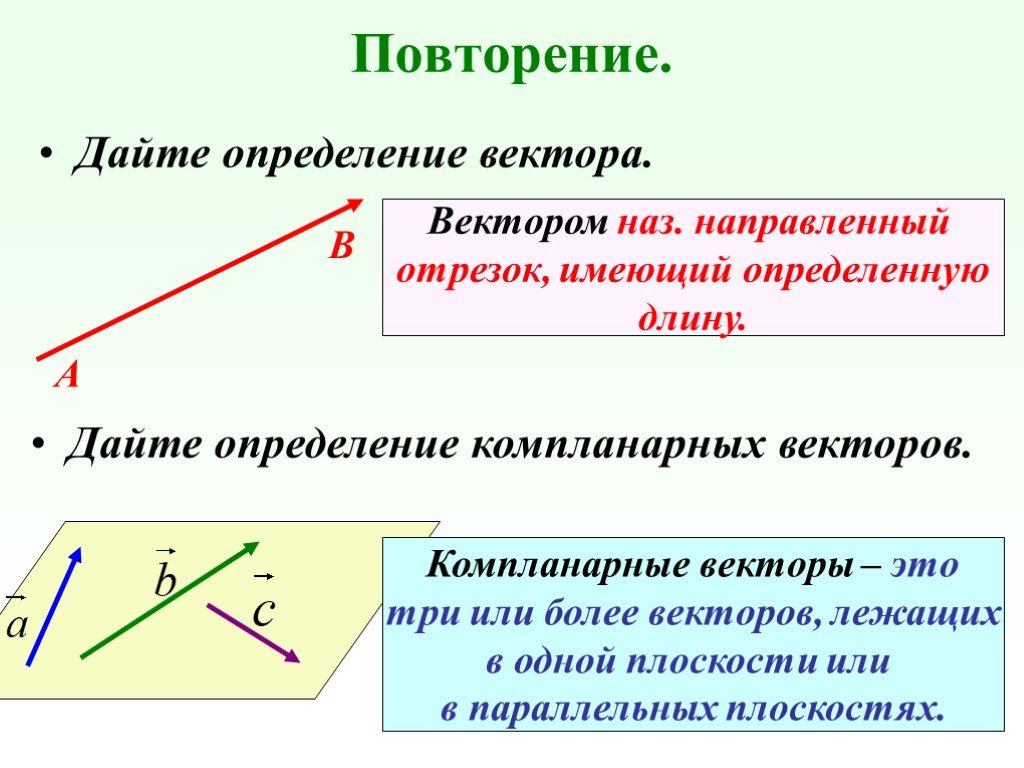
Разложение вектора по двум неколлинеарным векторам. Если векторы а и b коллинеарны и а 0, то существует такое число k, что b = ka. Любой вектор ...Разложение вектора по двум неколлинеарным векторам
Лемма: Если векторы а и b коллинеарны и а 0, то существует такое число k, что b = ka. Доказательство:. Теорема: Любой вектор можно разложить по ...Откладывание вектора от данной точки
Аннотация. Тема «ВЕКТОРЫ» рассчитана на учащихся 8 – 9 классов Презентация помогает учащимся применять свои знания не только в изучении геометрии, ...Откладывание вектора от данной точки
Назвать все изображенные векторы (векторы можно изображать двумя заглавными латинскими буквами или одной незаглавной). А R D L С К Y X H E M T с а. ...Координаты точки, середины отрезка
Цель :. Ввести понятие координатная плоскость, Развивать познавательную активность учащихся, любознательность, Способствовать развитию навыков применения ...Координаты на прямой
1м. Белка вылезла из дупла и бегает по стволу дерева вверх и вниз. Покажите где будет белка, если она удалится от дупла на 3м. Сколько ответов можно ...Координаты
Р= 3+3+4+4=? s=? А(4,6). Математика 4 класс. y x 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10. Разминка 4 * 12 + 12 Р 96 : 8 * 30 270 : 9 : 15 1000- 898 : 2 25 ...Умножение вектора на число
ЗАДАЧА№1 Найдите:. ЗАДАЧА№2 Докажите:. ЗАДАЧА№3. ABCD-прямоугольник AB=5; AD=12. Докажите: Найдите:. Умножение вектора на число. . Произведение любого ...Координаты на плоскости
История. Первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ...Координаты на плоскости
Рене Декарт Готфрид Вильгельм Лейбниц. Цели:. Образовательные: Познакомить учащихся с координатной плоскостью развитие умений находить координаты ...Координаты для координатной плоскости
Цели урока: Обучающая: познакомить учащихся с новыми понятиями: “координатная плоскость”, “система координат”, “прямоугольная система координат”, ...Координаты вокруг нас
ЦЕЛЬ:. Углубить знания о координатах. Узнать кто создал координаты и зачем. Узнать при каких целях используются координаты. Собрать и приготовить ...Координаты
Повторение. (-4) : (2)= (-3)∙(-2)= (-3)-(-3)= 3∙(-4)= (-3)∙1= (-1)∙(-2)= (-3)+(-2)= (-3)∙3= (-3)-(-2)= (-8) : (-2)= (-3)+(-2)= (-3)∙(-2)= (+3)∙(+2)=. ...Координаты на прямой
Координатной прямой называют прямую, у которой задано начало отсчета (точка O) ,единичный отрезок и стрелкой указано положительное направление. Прямые ...Скалярное произведение вектора
Физический смысл. Скалярное произведение векторов имеет простой физический смысл и связывает работу A, производимую постоянной силой при перемещении ...Координаты на прямой
Белка вылезла из дупла и бегает по стволу дерева вверх и вниз. Вопросы: - Что нужно знать, чтобы определить положение белки на дереве? - Достаточно ...Умножение вектора на число и т.д
. . Теорема 10.2. . Произведение любого вектора на число нуль есть нулевой вектор. Произведением нулевого вектора на любое число считается нулевой ...Координаты
Оставьте мне свои координаты. Что означает эта фраза? Что указано на билете пассажира? Можно ли данную информацию назвать «координатами» пассажира? ...Декартовы координаты на плоскости
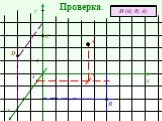
Я мыслю – следовательно, я существую. Рене Декарт Фото с сайта http://pimno.vspu.ru/Prodject/navigator/People/Dekart_Rene.htm. Отметьте точки A (1; ...Конспекты
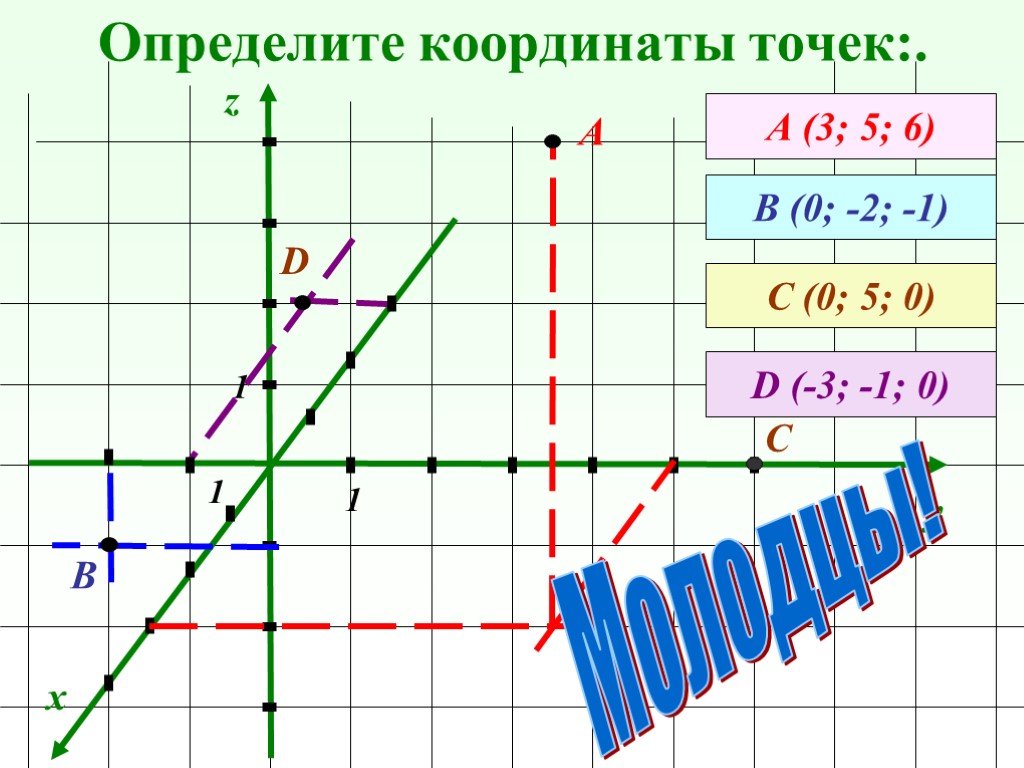
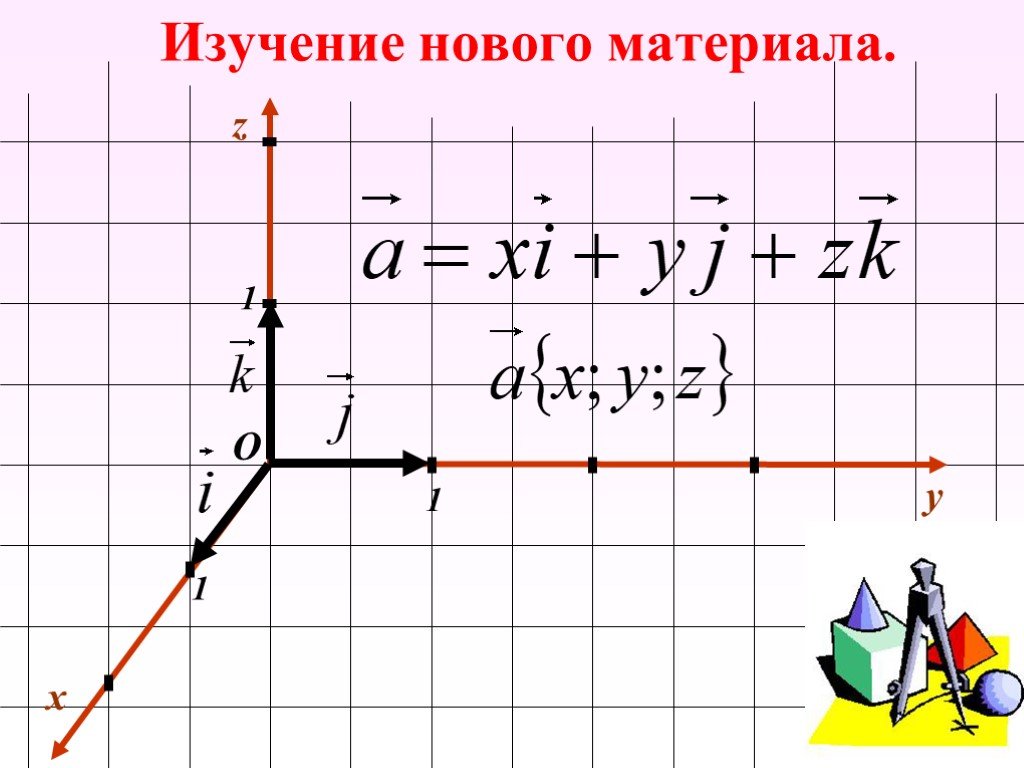
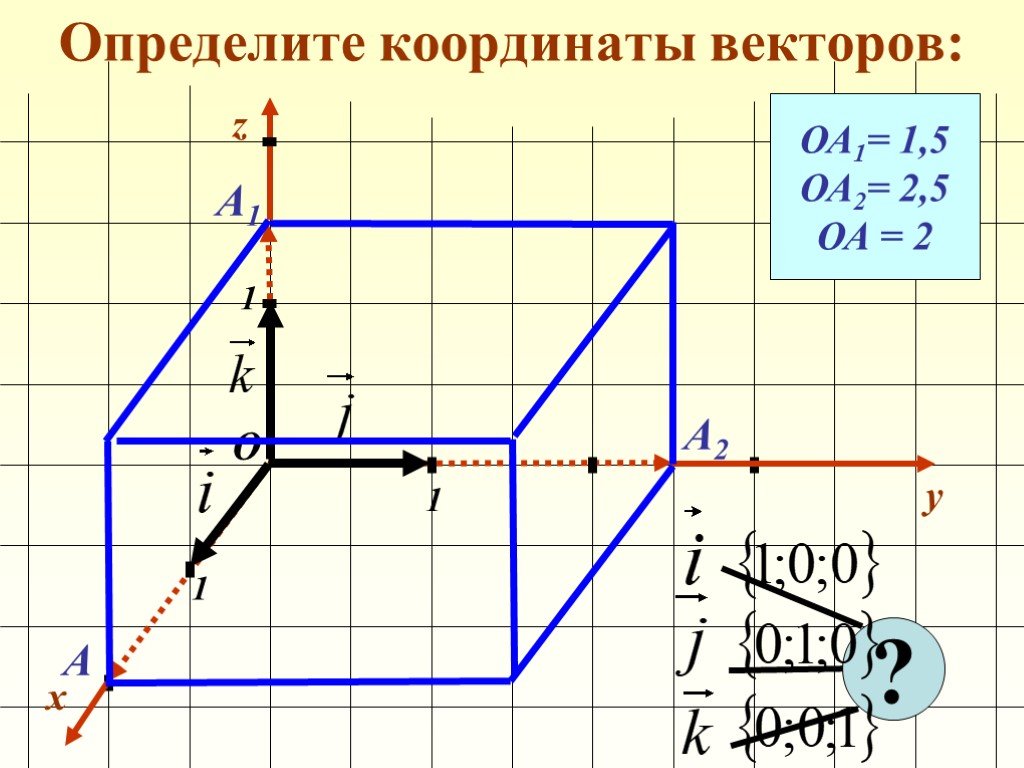
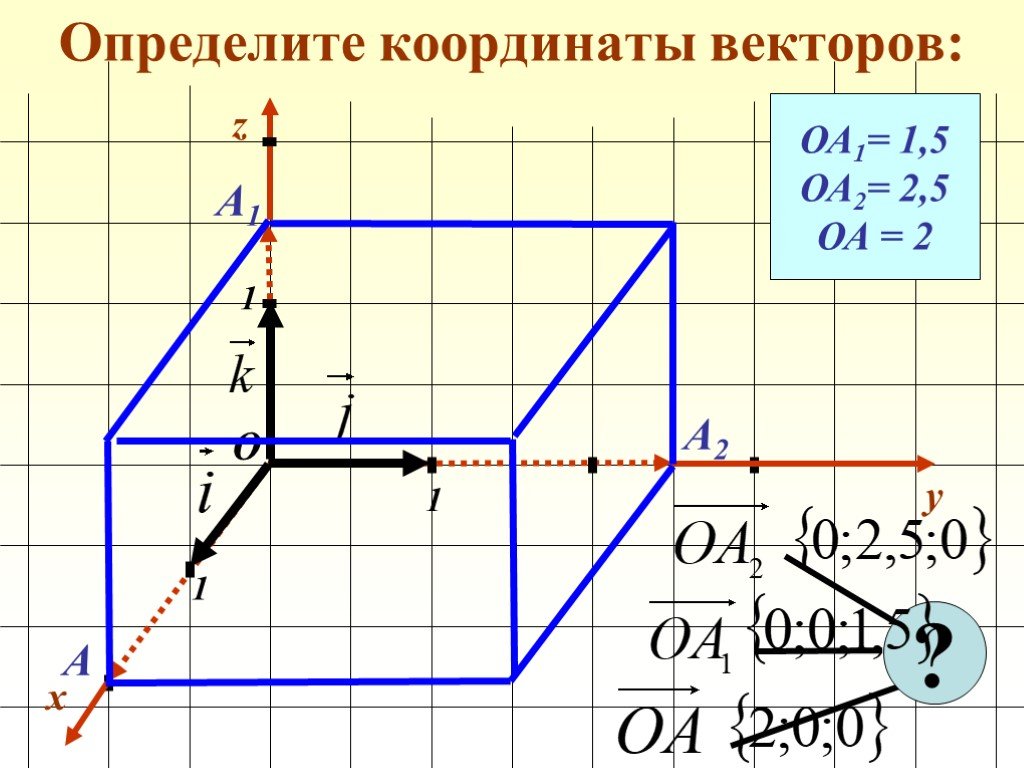
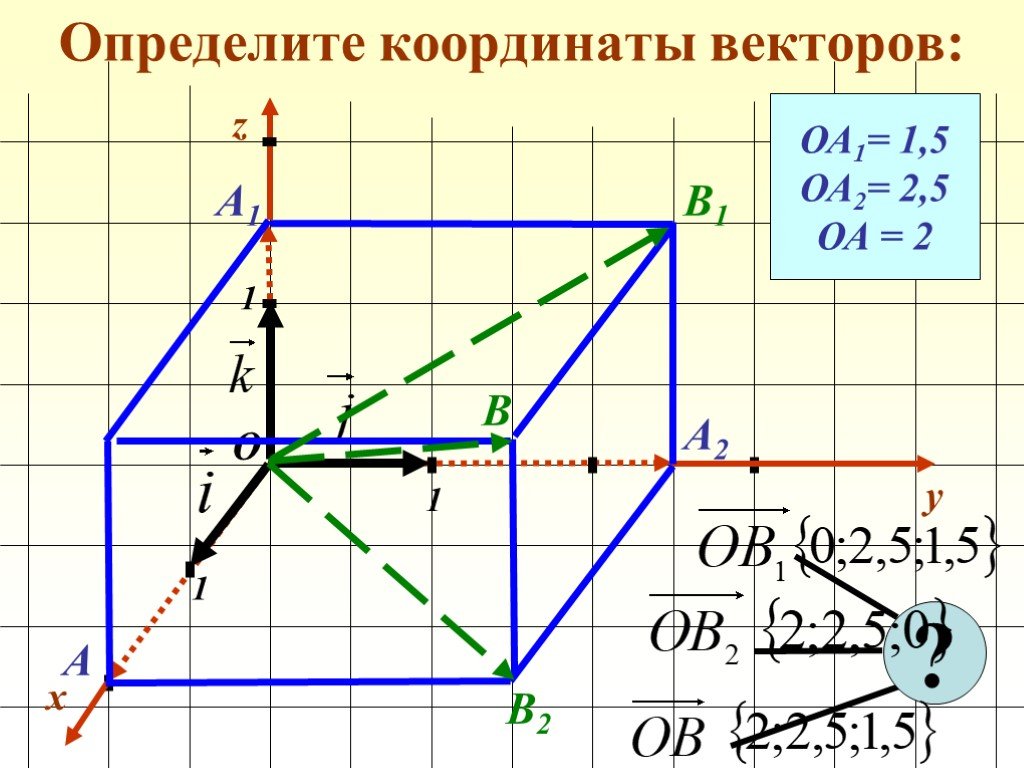
Координаты вектора
Автор –. Переяслова Наталья Владимировна, учитель математики. МОУ СОШ № 57 г. Астрахань. Предмет. – геометрия 9 класс. . Учебно-методическое ...Декартовы координаты в пространстве. Координаты вектора
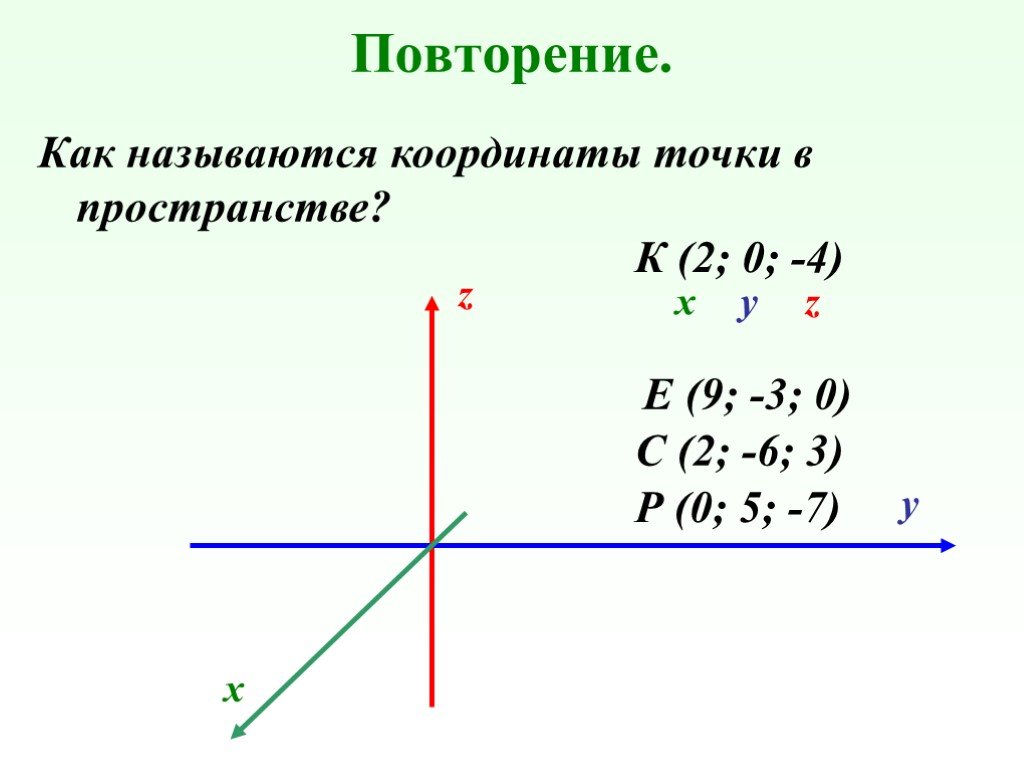
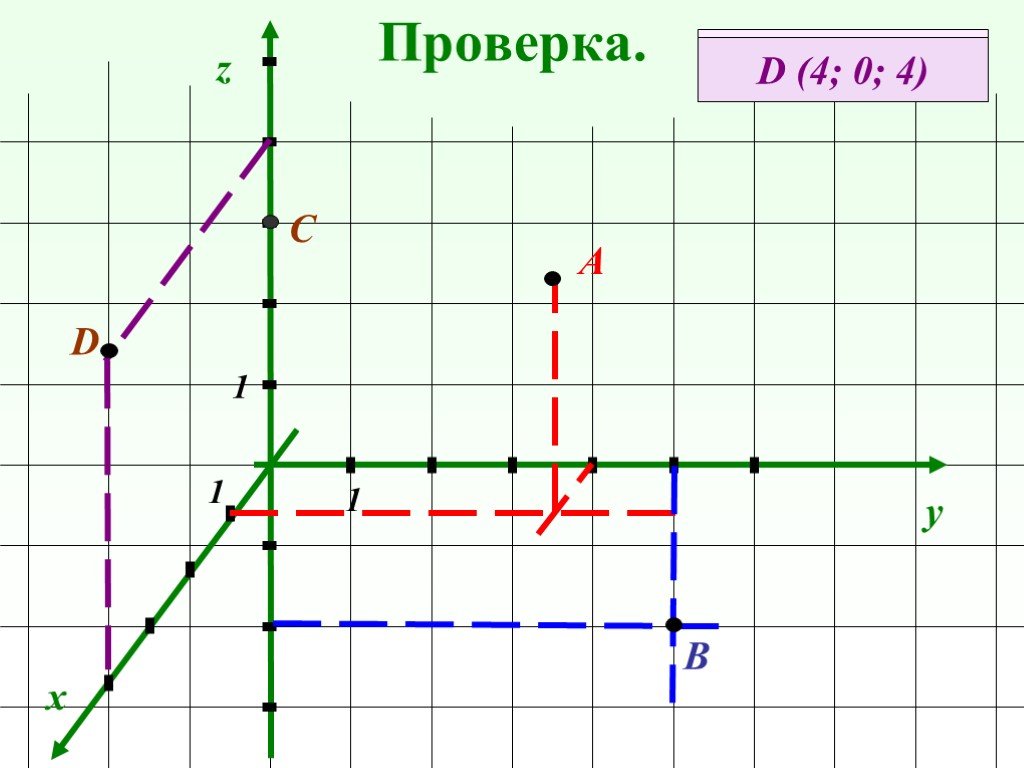
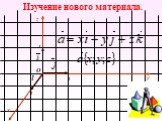
Тема урока: «. Декартовы координаты в пространстве. Координаты вектора». Цели урока:. 1) Образовательная:. напомнить учащимся,. как задается ...Числовой луч. Координаты точки на числовом луче
Урок математики, 4 класс. Тема: Числовой луч. Координаты точки на числовом луче. Цель. : Сформировать представление о понятиях «луч», «числовой ...Понятие вектора
Муниципальное общеобразовательное учреждение. «Завьяловская средняя общеобразовательная школа №1». Завьяловского района Алтайского края. ...Понятие вектора
Учитель математики - Юшина Раиса Алексеевна. . МБОУ СОШ № 18. . . Тема:. 9КЛ. . 2010. год. Тема:. Понятие ...Метод координат на плоскости. Координаты на прямой
Муниципальное бюджетное общеобразовательное учреждение. «Вечерняя сменная средняя общеобразовательная школа при ИУ». Конспект урока. Метод координат ...Координаты на прямой
Открытый урок по математике в 6 классе. "Координаты на прямой". Учитель высшей категории Емец Светлана Викторовна,. . МБОУ СОШ№ 29,г.Ставрополя. ...Координаты на прямой
. Тема урока: Координаты на прямой. Цели урока. - Определение координаты точки. - Реализация принципов связи теории и практики. - Развитие ...Координаты на прямой
Автор: Джалмухамбетова Дина Тулигеновна. Место работы: МБОУ «Седлистинская сош». Должность: Учитель математики и информатики. Тема урока: Координаты ...Координаты на прямой
Аскарова Татьяна Саядовна. учитель математики. МБОУ «Тимирязевская СОШ» Городецкий район, Нижегородская область. Конспект урока математики ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 ноября 2018
Категория:Математика
Классы:
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию