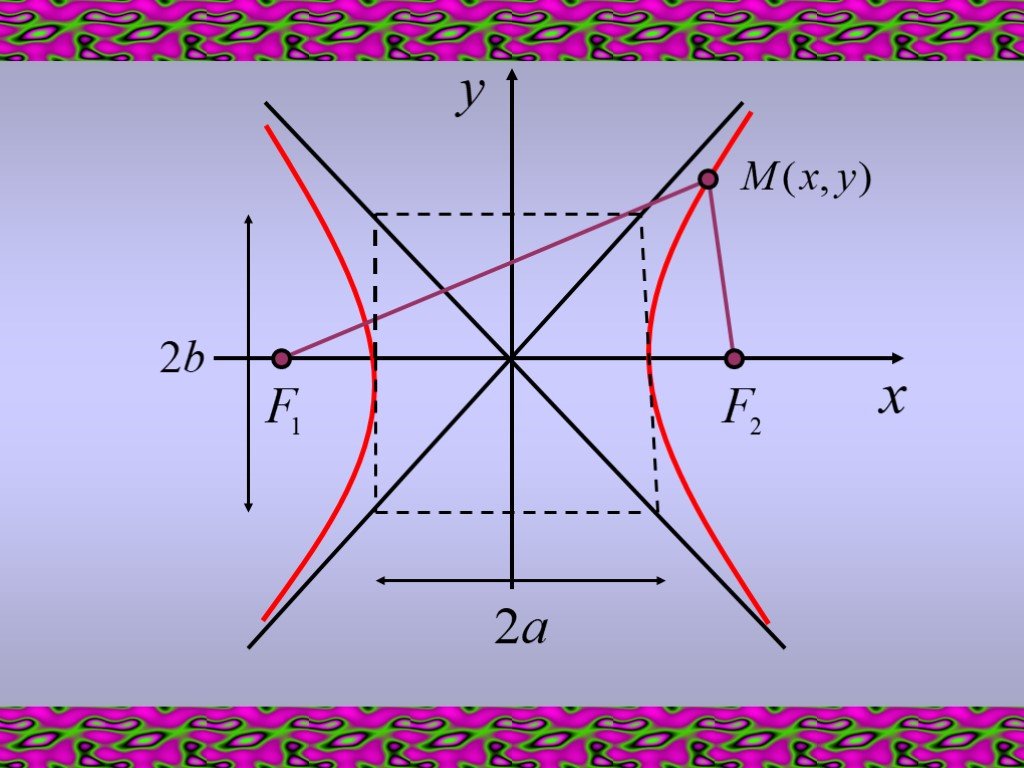
Презентация "Гипербола" по математике – проект, доклад

Скачать презентацию (0.2 Мб) Смотреть похожие презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Презентацию на тему "Гипербола" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).

Скачать презентацию (0.2 Мб) Смотреть похожие презентации

Слайды презентации

Слайд 1

4.4. ГИПЕРБОЛА

ГИПЕРБОЛОЙ называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (меньшая, чем расстояние между фокусами)

Слайд 3

Введем обозначения:

a – действительная полуось гиперболы b – мнимая полуось гиперболы

Для любой точки М(х,у), принадлежащей гиперболе, по определению выполняется равенство:

Слайд 4

Прямые, проходящие через начало координат и имеющие угловые коэффициенты

называются асимптотами гиперболы.

Асимптоты делят плоскость на 4 области, в двух из которых расположена гипербола.

Точки гиперболы по мере удавления от оси у приближаются к асимптотам, т.е. расстояние между точками гиперболы и асимптотой при увеличении х уменьшается и стремится к нулю.

Слайд 5

ТЕОРЕМА Для того, чтобы точка М(х,у) принадлежала гиперболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению

где 2

Слайд 6

Покажем, что координаты точки, принадлежащей гиперболе, удовлетворяют уравнению (2).

Т.к. точка М(х,у) принадлежит гиперболе, то по определению гиперболы, должно выполнятся условие

Выразим каждое расстояние по формуле расстояния между двумя точками:

Слайд 7

Тогда:

Слайд 8

Возводим в квадрат обе части выражения:

Слайд 9

Возводим в еще раз квадрат:

Делим все выражение на

Слайд 10

каноническое уравнение гиперболы

Слайд 11

Отношение фокусного расстояния к длине действительной оси гиперболы называется ЭКСЦЕНТРИСИТЕТОМ

Слайд 12

Для гиперболы

Следовательно, для гиперболы

Чем меньше отношение мнимой и действительной полуосей, тем меньше эксцентриситет и тем более гипербола будет прижата к оси х, и наоборот.

Список похожих презентаций

Синус, косинус, тангенс и котангенс, алгебра,

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.