Презентация "Предел числовой последовательности" по математике – проект, доклад
Презентацию на тему "Предел числовой последовательности" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
Предел числовой последовательности
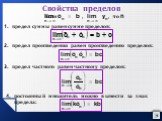
Назовем числовой последовательностью числовую функцию, заданную на множестве натуральных чисел: Значение n будем называть номером члена , а само число ...Предел последовательности чисел
Определение 1. Функцию вида у= f (х), х ϵ Ν называют функцией натурального аргумента или числовой последовательностью и обозначают у = f (n) или у1, ...Предел
Оглавление. Титульная страница Оглавление Вступление Предел переменной величины Основные свойства пределов Предел функции в точке Понятие о непрерывности ...Числовые последовательности
Числовые последовательности. Функцию вида y=f(x), где xєΝ, называют функцией натурального аргумента или числовой последовательностью и обозначают ...Числовая окружность. Запись чисел числовой окружности
+ – 0;2П; 4П. - 2П; -4П. П -11П 6 6 П -7П 4 4 П -5П 3 3 2П -4П 3 3 3П -4П 4 3 5П -7П 6 6 7П -5П 6 6 5П -3П 4 4 4П -2П 3 3 5П -П 3 3 7П -П 4 4 11П ...Точки на числовой окружности
. оглавление. Числовая окружность на координатной плоскости Дидактические игры Тригонометр. Литература. Центр числовой окружности совместим. с центром ...Представление числовой информации с помощью систем счисления
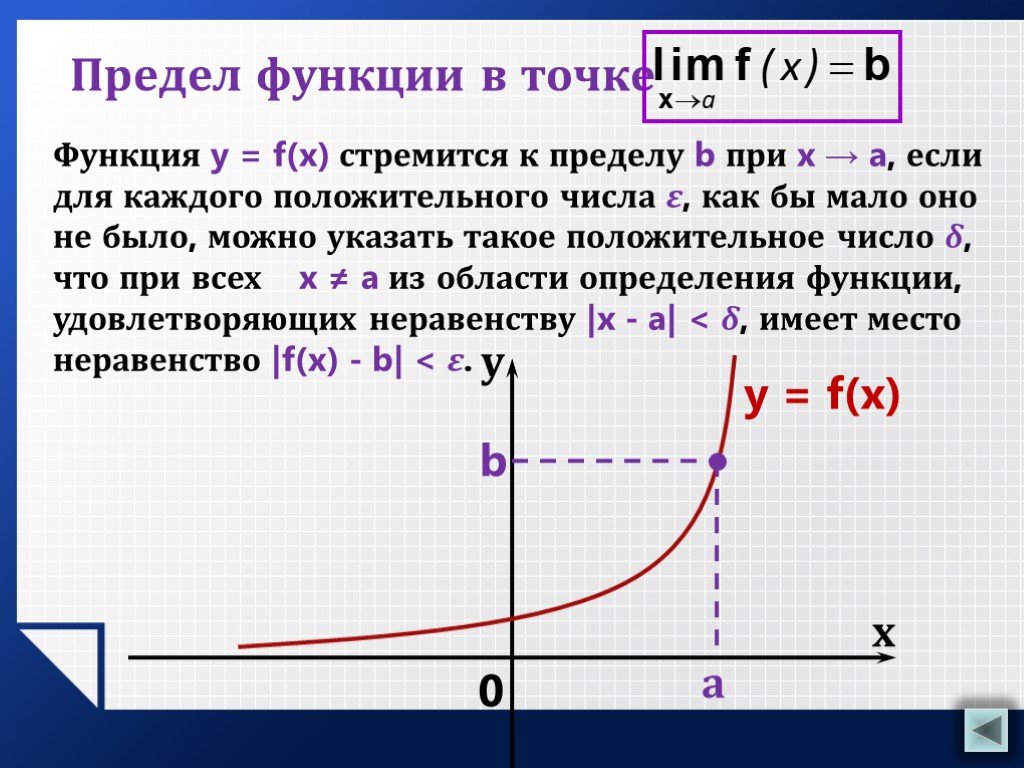
Система счисления. - это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых ...Предел функции в точке
Рассмотрим функции, графики которых изображены на следующих рисунках:. Во всех трех случаях изображена одна и та же кривая, но все же изображают они ...Предел функции в точке
Одна и та же кривая, три разные функции. Отличие – поведение в точке х = а. f(a) – не существует, т.к. в точке х =а функция у = f(х) не определена. ...Предел функции в бесконечности и в точке
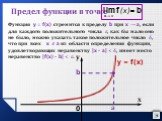
Число А называется пределом функции у=f(x), при х стремящемся к бесконечности, если для любого, сколь угодно малого числа ε>0, найдется такое положительное ...Предел функции
Содержание. Предел функции в точке Односторонние пределы Предел функции при x стремящемся к бесконечности Основные теоремы о пределах Вычисление пределов ...Предел переменной величины
f(x)=x+2, при х 1. f(0,9)=2,9 f(0,99)=2,99 f(0,999)=2,999 f(1,1)=3,1 f(1,01)=3,101. Определение. Постоянная величина а называется пределом переменной ...Числовые последовательности
Что узнаете нового. Определение числовой последовательности Способы задания Стандартные упражнения. Последовательности. Угадайте закономерность. Способы ...Числовые последовательности
Ты можешь стать умнее тремя путями: путем опыта – это самый горький путь; путем подражания – это самый легкий путь; путем размышления – это самый ...Синус, косинус, тангенс и котангенс, алгебра,
Синус и косинус. Что будем изучать:. Определение синуса и косинуса. Определение тангенса и котангенса. Основное тригонометрическое тождество. Примеры ...Матричная алгебра в экономике
Содержание:. ● Вступление ● Что такое матрицы и операции над ними ● Решение экономических задач матричным методом ● Заключение ● Список используемой ...Реляционная алгебра – механизм манипулирования реляционными данными
Две группы операций РА. теоретико-множественные операции специальные реляционные операции. Теоретико-множественные операции. объединения отношений; ...ГИА 2013. Модуль алгебра №6
ГИА – 2013 г. Модуль «Алгебра» №6. «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. ...ГИА 2013. Модуль алгебра №8
Модуль «Алгебра» №8. Повторение (4). Решите неравенство 7+2(х-4)≥х+4. Ответ: [-3;+∞). Повторение (подсказка). При решении неравенства можно переносить ...Конспекты
Определение числовой функции. Область определения, область значений функции
Муниципальное общеобразовательное учреждение. Оковецкая средняя общеобразовательная школа. Селижаровский район Тверская область. Тема урока:. ...Определение числовой функции. Виды. Свойства, графики числовых функций. Способы задания функции
Кейс технологии. Урок алгебры. . Калинина Ирина Борисовна. учитель математики. МАОУ ГИМНАЗИЯ №8 г. Перми. РАЗРАБОТКА УРОКА. c. применением ...Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции
Министерство образования и науки Самарской области. . ГБОУ СПО «Безенчукский аграрный техникум». Конспект занятия. ТЕМА. Предел функции ...Предел функции в точке
Урок алгебры в 10 классе по теме «Предел функции в точке». Цель урока:. формирование у учащихся наглядно – интуитивных представлений о пределе ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 декабря 2018
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию