Презентация "Четыре замечательные точки треугольника" по математике – проект, доклад
Презентацию на тему "Четыре замечательные точки треугольника" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 11 слайд(ов).
Слайды презентации
Список похожих презентаций
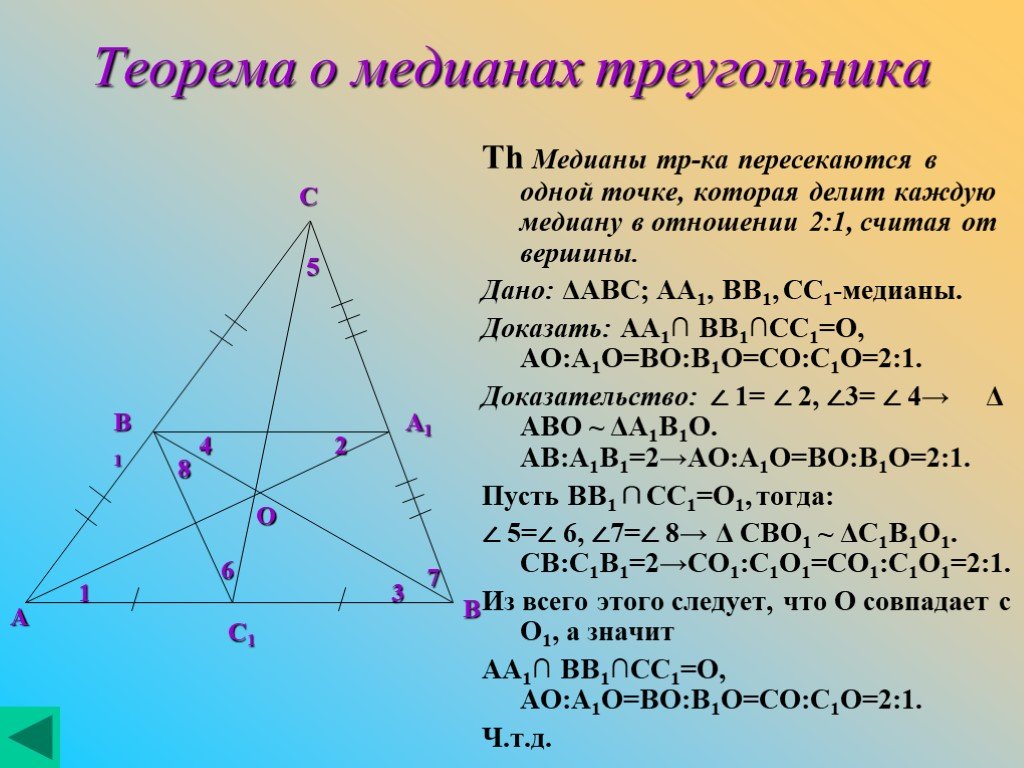
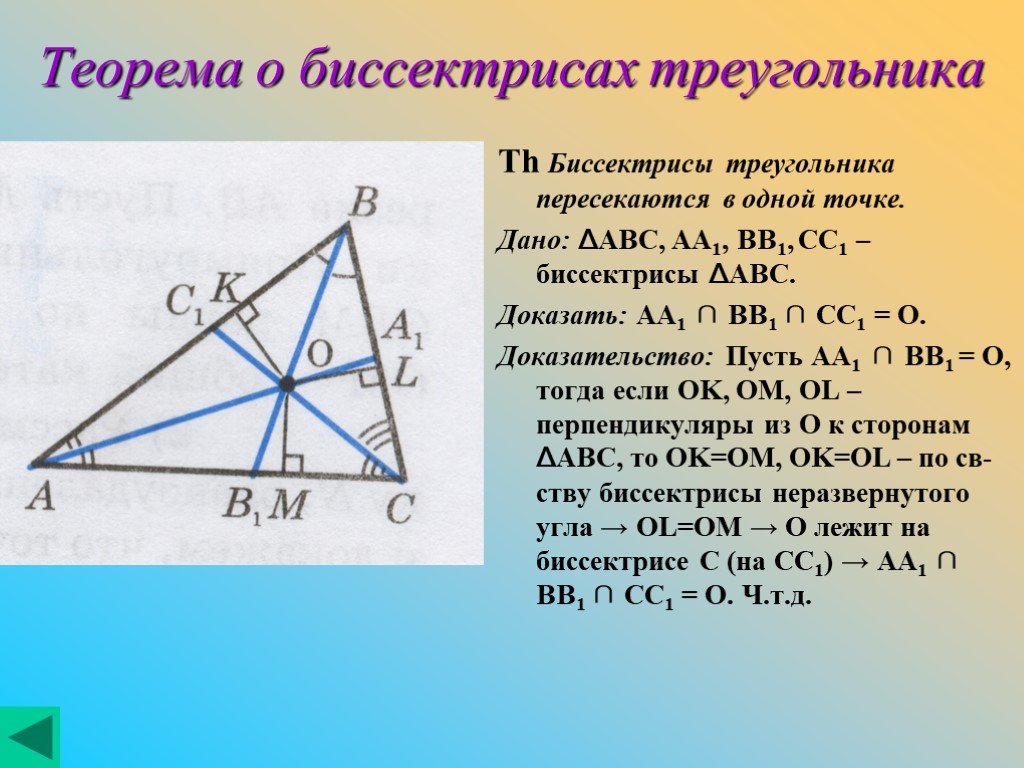
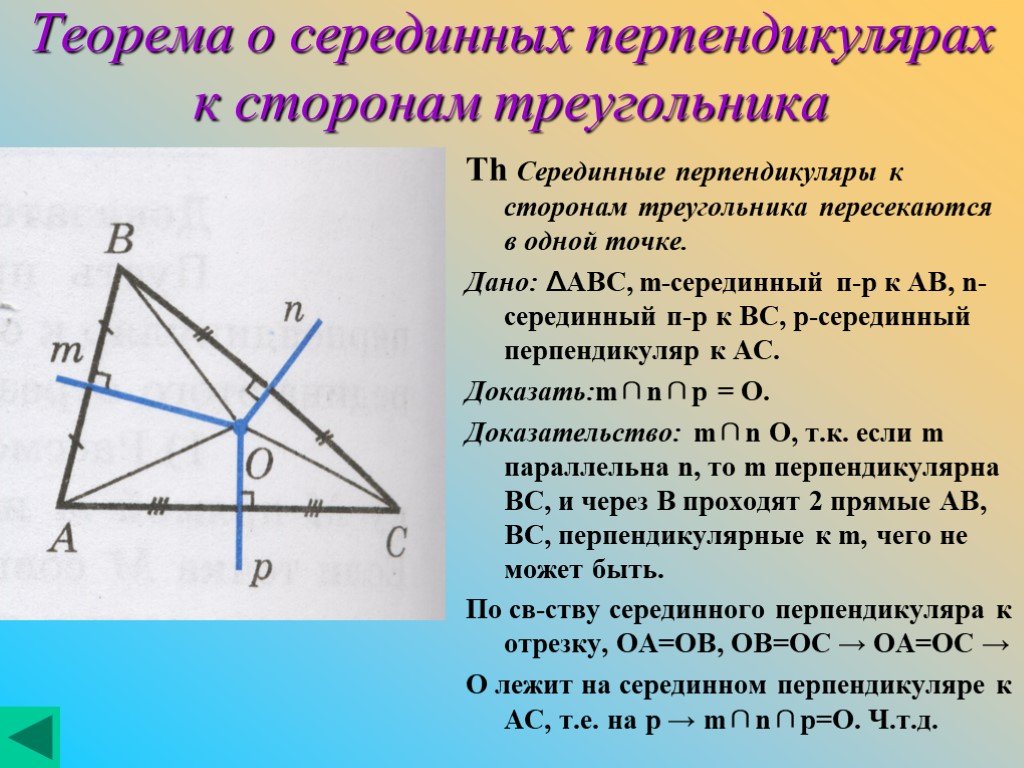
Четыре замечательные точки треугольника
A D B C. ABCD – квадрат. Назовите пары перпендикулярных прямых. Задача № 1. M N Задача №2. а Н А. Отрезок АН – перпендикуляр, опущенный из точки А ...Расстояние от точки до прямой и плоскости
РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ И ПЛОСКОСТЯМИ. Расстоянием между двумя непересекающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного ...Чему равна сумма углов треугольника
Вдохновение нужно в геометрии не меньше, чем в поэзии. А.С.Пушкин. Цели урока:. Изучить утверждение о сумме углов треугольника и формировать навык ...Теорема Пифагора для прямоугольного треугольника
Пифагор Самосский — древнегреческий философ, математик и мистик, создатель религиозно -философской школы пифагор - ейцев. Историю жизни Пифагора трудно ...Сумма углов треугольника 2
Цель урока:. Закрепить и проверить знания учащихся по теме «Свойства углов, образованных при пересечении двух параллельных прямых третьей» и «Признаки ...Сумма углов треугольника
Цели урока:. 1. Закрепить и проверить знания учащихся по теме : «Свойство углов образованных при пересечении двух параллельных прямых третьей и признаки ...Соотношения между сторонами и углами треугольника
Теорема о площади треугольников. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Стороны треугольника пропорцианальны ...Свойство углов треугольника
Виды треугольников. B A C E F D N M K Остроугольный Прямоугольный Тупоугольный. Верно ли, что:. - остроугольный треугольник – это треугольник у которого ...Геометрия в звездном небе. Свойство углов треугольника
Правила для членов клуба «ПИФАГОР»: Активно знакомиться с геометрическими терминами. 2. Радостно узнавать геометрические фигуры в повседневной жизни. ...Высота треугольника
Все геометрические фигуры разделить на две группы. Назвать эти группы. Многоугольники. Немногоугольники. пятиугольник четырёхугольник треугольник ...Внешний угол треугольника. Теорема о внешнем угле треугольника
I. Cумма углов треугольника. 1. На доске доказать теорему о сумме углов треугольника: Сумма углов треугольника равна 1800 2. Решить задачу № 749 (чёт ...Внешний угол треугольника
Общий вид внешнего угла. Понятие. Свойство внешнего угла. Внешний угол. Внешний угол треугольника. Угол, смежный с каким–нибудь углом треугольника, ...Внешний угол треугольника
Треугольник (музыкальный инструмент). Жесткость треугольников. Бермудский треугольник. ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА. У треугольника может быть два тупых ...Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Теорема 2. В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны ...Свойства равнобедренного треугольника
Медиана треугольника. Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса треугольника. ...Свойства равнобедренного треугольника
план урока:. Решение задач по готовым чертежам Виды треугольников по длинам сторон Доказательство теоремы Решение задач Самостоятельная работа. Решить ...Две замечательные теоремы планеметрии
Цель:. Доказав теоремы Менелая и Чевы, исследовать их применение при решении задач. Задачи:. Показать применение теорем Менелая и Чевы при решении ...Соотношения между сторонами и углами прямоугольного треугольника
ОТНОШЕНИЕ ПРОТИВОЛЕЖАЩЕГО КАТЕТА К ГИПОТЕНУЗЕ. ТО, ЧТО ВЫРАЖАЕТ ТЕОРЕМА: «ЕСЛИ ДВА УГЛА ОДНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ДВУМ УГЛАМ ДРУГОГО ...Задачи на вычисление площади треугольника
Девиз урока: «Кто ищет – тот всегда найдет…». Личностные цели. самостоятельно добывать знания, анализировать и обобщать; уверенно и грамотно выражать ...Средняя линия треугольника
Каким образом эти треугольники поделили на две группы? А B C. Отрезок, соединяющий середины двух сторон, называют СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА. Задача: ...Конспекты
Замечательные точки треугольника
Министерство образования Республики Беларусь. Учреждение образования. Белорусский Государственный Педагогический Университет имени Максима Танка. ...Сумма углов треугольника
ПЛАН – КОНСПЕКТ УРОКА. «Сумма углов треугольника». ФИО. Васильева Елена Викторовна. . Место работы. ГБОУ СОШ № 8 п.г.т. Алексеевка г.о. ...Сумма углов треугольника
МОУ Берёзовская средняя общеобразовательная школа. Галичского района Костромской области. Учитель Баринова Марина Александровна. Предмет: геометрия. ...Сумма углов треугольника
Скороварова Любовь Витальевна учитель математики первой категории МБОУ ООШ с. Никольское Усманского района Липецкой области. Конспект урока на ...Сумма углов треугольника
Муниципальное казенное общеобразовательное учреждение – средняя общеобразовательная школа с. Андреевка Екатериновского района Саратовской области. ...Средняя линия треугольника
Шамотина Л.В. . . ГБОУ СОШ № 443. Фрунзенский район. СПб. . План-конспект урока геометрии в 8 классе по теме. . «Средняя линия треугольника». ...Соотношения между сторонами и углами прямоугольного треугольника
МОУ «Лицей №31». Методическая разработка урока. по геометрии в VIII. классе. по проблеме: «Личностно-ориентированный подход ...Соотношение между сторонами и углами треугольника
Фрагмент урока по теме: «Соотношение между сторонами и углами треугольника» (9 класс, учебник «Геометрия 7 – 9», Л. С. Атанасян). Автор:. учитель ...Медианы, биссектрисы и высоты треугольника
Негосударственное общеобразовательное учреждение. «Миасская средняя школа – интернат № 14 ОАО «РЖД»». Челябинской области. Конспект ...Медиана, биссектриса, высота треугольника
Урок по теме «Медиана, биссектриса, высота треугольника». Разработала учитель математики МБОУ СОШ №2 с. Александров-Гай Уразова Ольга Владимировна. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 октября 2018
Категория:Математика
Содержит:11 слайд(ов)
Поделись с друзьями:
Скачать презентацию