Презентация "Действительные числа (2)" по математике – проект, доклад
Презентацию на тему "Действительные числа (2)" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
Действительные числа и их свойства
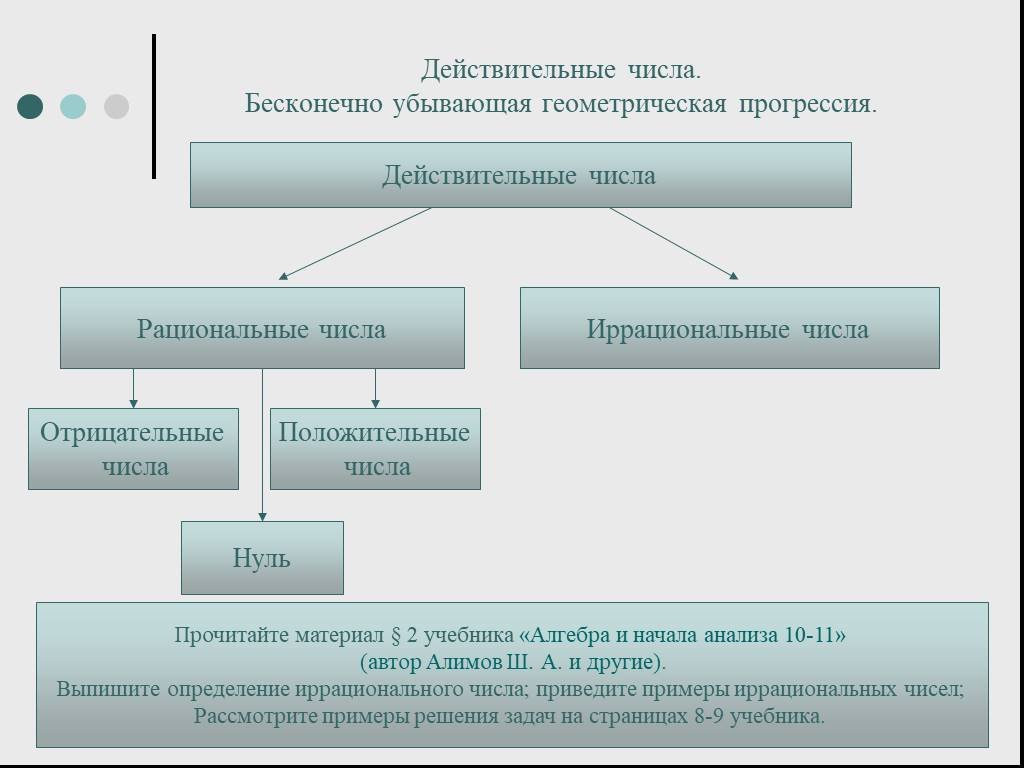
Действительные числа образуют совокупность элементов, обладающую следующими свойствами. Если a и b - действительные числа (алгебраические, рациональные, ...Действительные числа и преобразования алгебраических выражений
Действительные числа и преобразования алгебраических выражений. Цель урока:. Повторяем Различаем Развиваем Оцениваем. Дома: теория (10) (3). Натуральные ...Действительные числа
На первых этапах существования человеческого общества числа, открытые в процессе практической деятельности, служили для примитивного счета предметов, ...Действительные числа
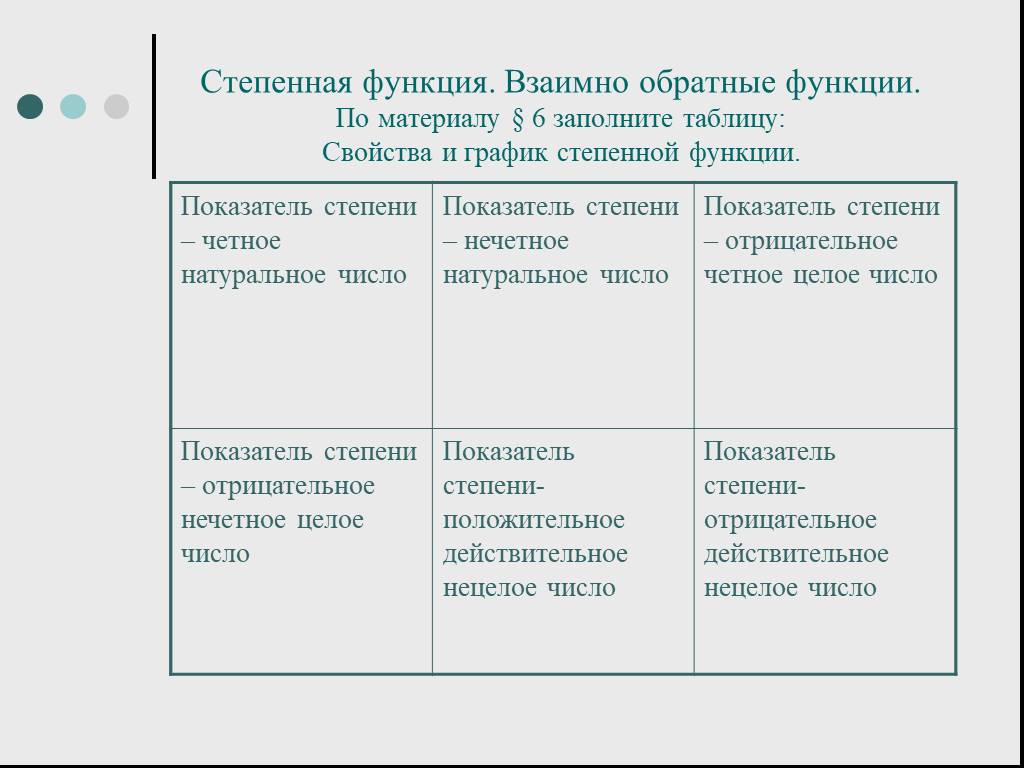
иметь понятия об: иррациональных числах; множестве действительных чисел; модуле действительного числа; уметь выполнять : вычисления с иррациональными ...Действительные числа
Этапы развития понятия числа. Геометрическое представление о числах как отрезках приводит к расширению множества Q до множества вещественных (или ...Действительные числа
Числовые множества. Множество натуральных чисел. Натуральные числа - это числа счета. N={1,2,…n,…}. Заметим, что множество натуральных чисел замкнуто ...Квадрат и куб числа
Прочитайте выражения. 3 * 3 5 * 5 6 * 6. Эти выражения в буквенной форме имеют вид n * n. Произведение n * n называют квадратом n числа и обозначают ...Иррациональные числа в древности и средние века
Чисел рациональных из множества Q не хватает для того, чтобы сделать числовую прямую сплошной, или, как говорят математики, непрерывной. Нам нужны ...Как появились цифры и числа
«Мир построен на силе чисел» Пифагор. Можно ли представить мир без чисел? - покупки; - определение времени; - номера телефона и др. Люди так часто ...Золотое сечение и числа Фибоначи
. 1+1=2 1+2=3 2+3=5 3+5=8 5+8=13 8+13=21 13+21=34 21+34=55 34+55=89 55+89=144. 13:8=1,625 21:13=1,615… 55:34=1,617.. 144:89=1,6179… 610:377=1,618. ...Именованные числа
Результат теста. Верно: 14 Ошибки: 0 Отметка: 5. Время: 1 мин. 16 сек. ещё исправить. Найди правильный ответ и щелкни по нему. 25 км 30 м 25030м 2530м ...Кто придумал отрицательные числа и зачем они нужны?
4 1 _. Так зачем же нужны отрицательные числа? Дробь. Отрицательные числа. Имущество +. Долг, недостача -. Диофант III в. н. э. Ши Хуан Ди. Китайский ...Задачи на нахождение числа по дроби
Думать - коллективно! Решать - оперативно! Отвечать - доказательно! Бороться - старательно! И открытия нас ждут обязательно! Лист учета. Проверка ...Взаимно простые числа
В СТРАНЕ СМЕШАРИКОВ. оглавление. ЦЕЛИ И ЗАДАЧИ ПЛАН УРОКА ИТОГИ ДОМАШНЕЕ ЗАДАНИЕ ТЕМА УРОКА ОБОРУДОВАНИЕ. тема урока. взаимно простые числа. план ...Возведение в степень. Куб и квадрат числа
Устно. Упростить выражение: 25х + 15 х; 12у – 3у; 9k + 9k – 4k; 80c-35c-14c; 8d+d-9d; 163 + 37v + 18v. Решить уравнение: 7х+2х = 918; 5а-3а = 222; ...Взаимно обратные числа
Дать определение взаимно обратных чисел; Научить находить числа, обратные данным, представленных в виде смешанных чисел, десятичных дробей. Цели и ...Взаимно обратные числа
Цель урока:. дать определение взаимно обратных чисел. научить находить число, обратное данному. развивать логическое мышление. Развитие логического ...Вектор 2
Геометрия. 8 класс Авторы: Л.С.Атанасян, В.Ф.Бутузов и др. Издательство: Москва. Просвещение. Тема: «Векторы». Урок изучения нового материала. Изучение ...Арабские цифры и числа
. ...Конспекты
Двузначные числа (приём вычисления для случаев вида 36 + 2)
МОУ « СОШ №12 г.Балашова Саратовской области». Урок математики. 1 класс. УМК «Гармония». Двузначные числа. (приём вычисления для случаев ...Действительные числа
МОБУ « Комаровская СОШ им. В.М.Устиченко». Конспект урока по алгебре. в 8 классе. Тема урока:. Действительные числа. Максакова ...Иррациональные числа. Действительные числа
Урок математики в 8 классе. Тема урока:. Иррациональные числа. Действительные числа. Синиченкова Галина Алексеевна. ...Деление многозначного числа на однозначное число (вида 312 : 3)
Урок математики 3 класс. Тип урока. : ОНЗ. Тема:. «Деление многозначного числа на однозначное число (вида 312 : 3).». Основные цели:. 1) формировать ...Закрепление. Умножение числа 2
Урок математики в 1 классе. Родина Марина Николаевна. Учитель математики в начальной школе. Ленинградская область. Город федерального значения ...Вычитание числа 2
Учитель:. Щипцова Светлана Александровна. Место работы:. МБОУ г. Астрахани «СОШ № 61». Класс:. 1. . Предмет:. Математика. УМК:. «Начальная ...Закрепление таблицы умножения и деления на 2
Предмет: математика. Класс: 2 класс. Тема урока:. «Закрепление таблицы умножения и деления на 2». . Программа: « Школа России», автор Моро М.И. ...задачи на уменьшение числа на несколько единиц
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К УРОКУ. ТЕМА: задачи на уменьшение числа на несколько единиц (на два множества). РЕШАЕМЫЕ ПРОБЛЕМЫ, ЦЕЛИ:. . -. образовательные. ...Задачи на увеличение и уменьшение данного числа на несколько единиц. Закрепление
Конспект урока математики во 2 классе (специальном коррекционном 8 вида). Тема. :. «Задачи на увеличение и уменьшение данного числа на несколько ...Десяток. Двузначные числа
УМК «Гармония» 1 класс. . Тема:. «Десяток. Двузначные числа». Автор: Хохлова Ирина Борисовна, учитель. . начальных классов. МБОУ ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 мая 2019
Категория:Математика
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию