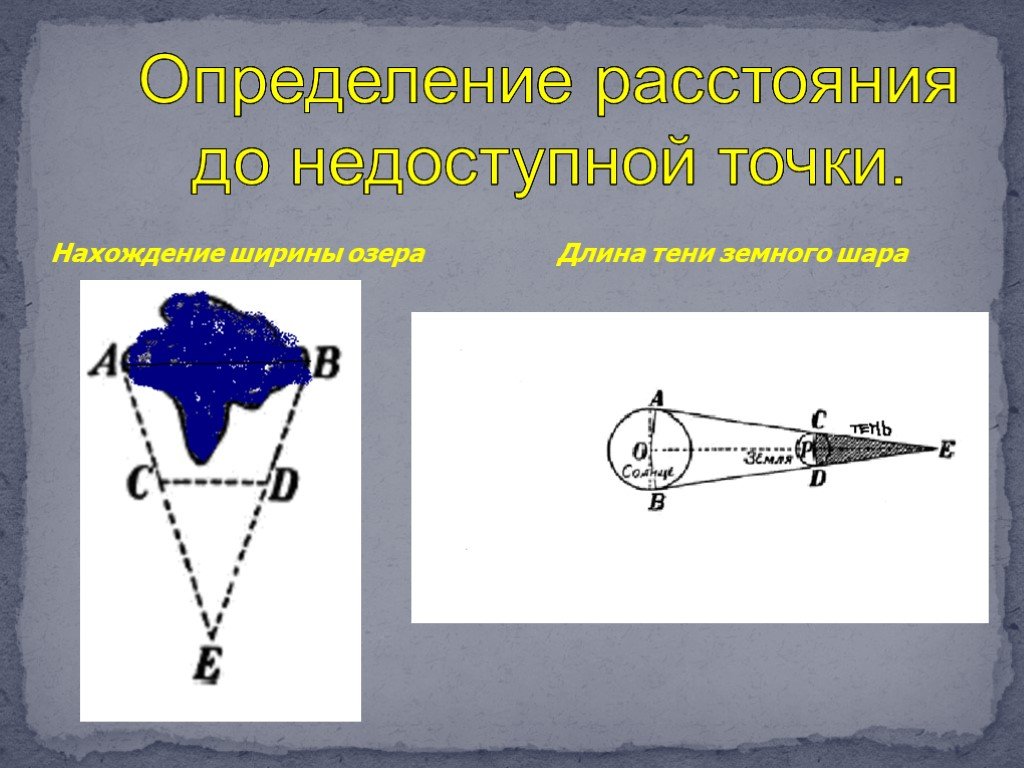
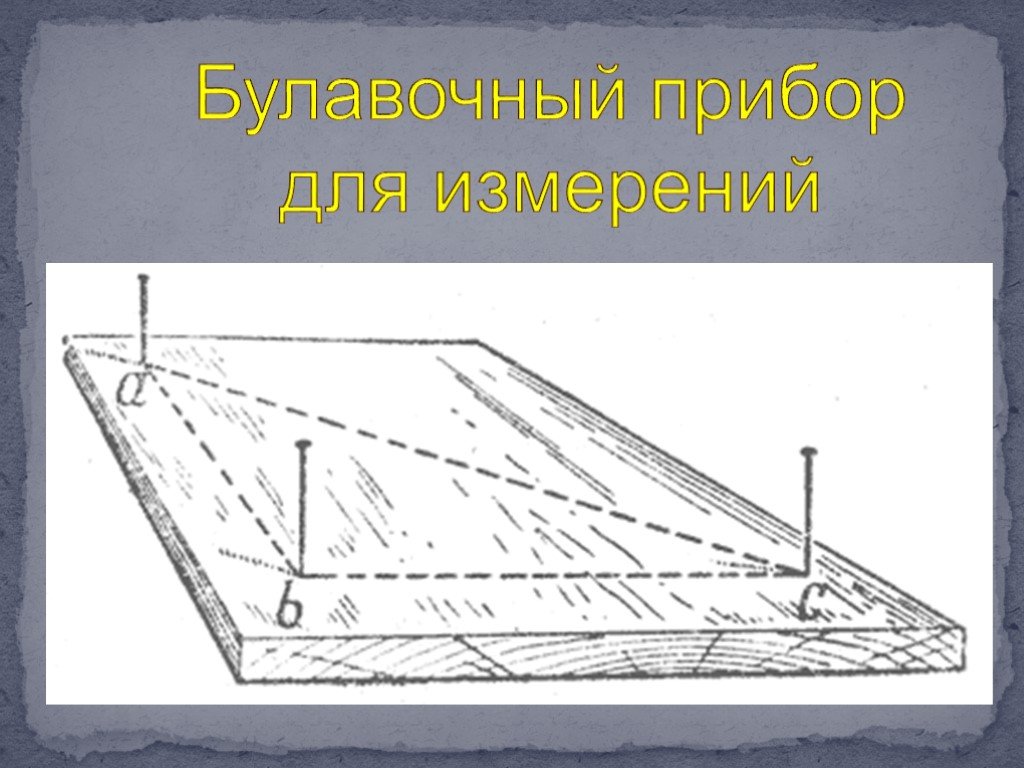
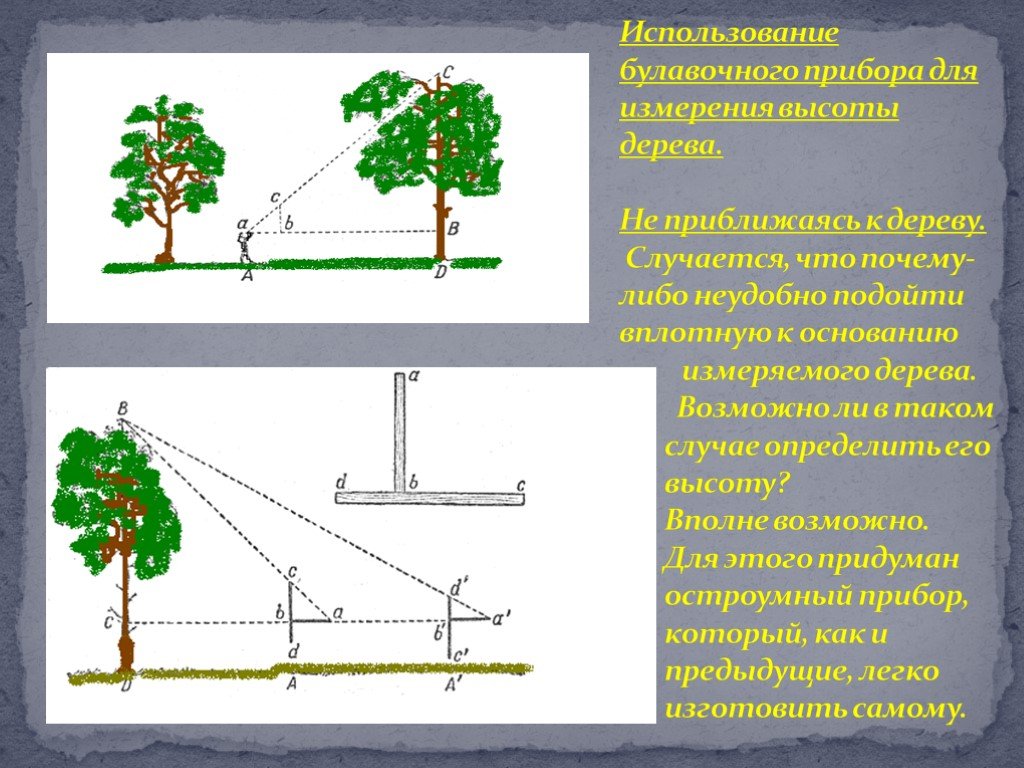
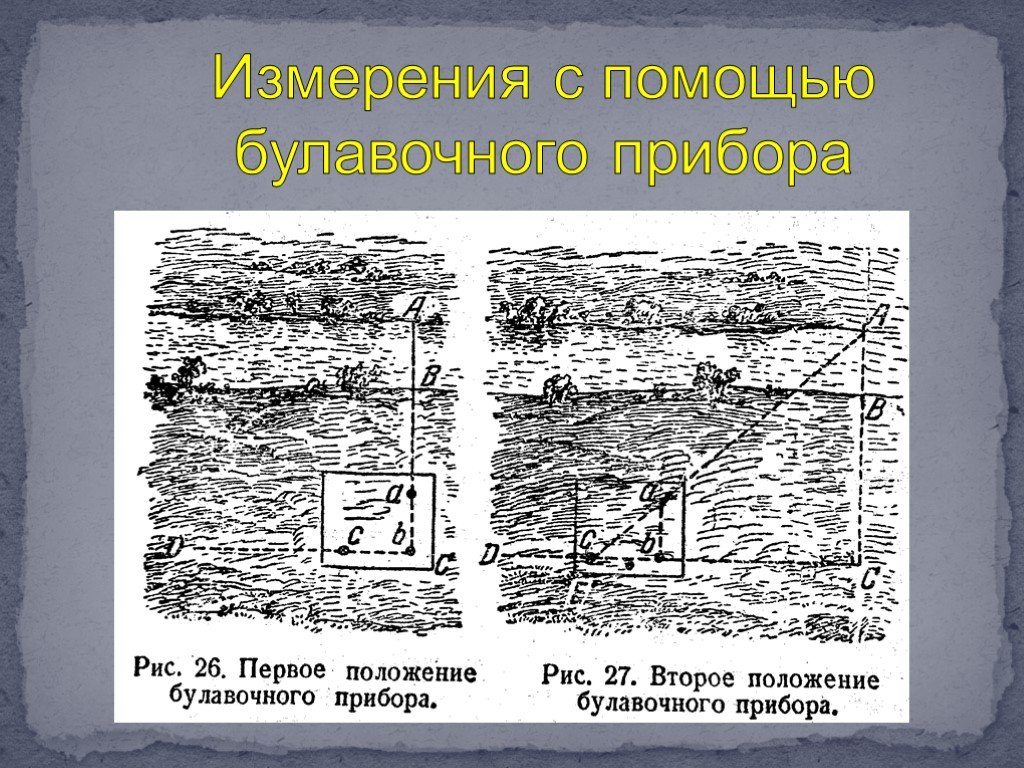
Презентация "Практическое применение подобия треугольников" по математике – проект, доклад
Презентацию на тему "Практическое применение подобия треугольников" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 31 слайд(ов).
Слайды презентации
Список похожих презентаций
Практическое применение подобия треугольников
СКАЗКА ЛОЖЬ, ДА В НЕЙ НАМЕК…. Был День рождения Шрека и Фиона решила отметить его несколько необычно. После долгого рабочего дня, Шрек пришёл домой ...Практическое применение подобия треугольников
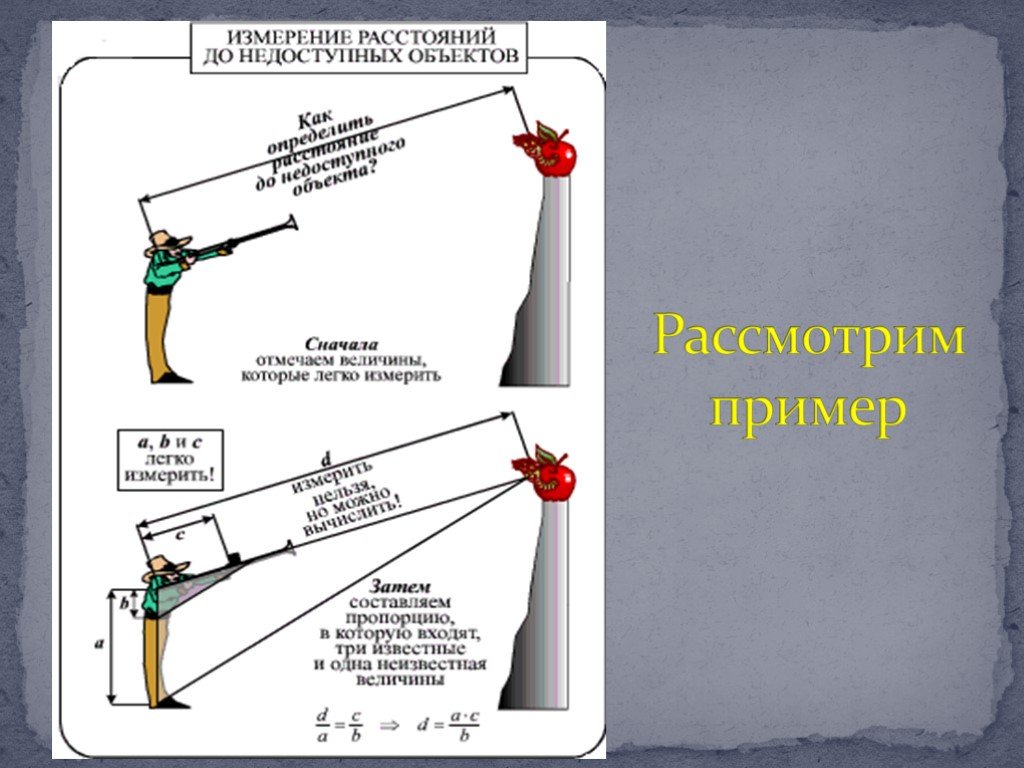
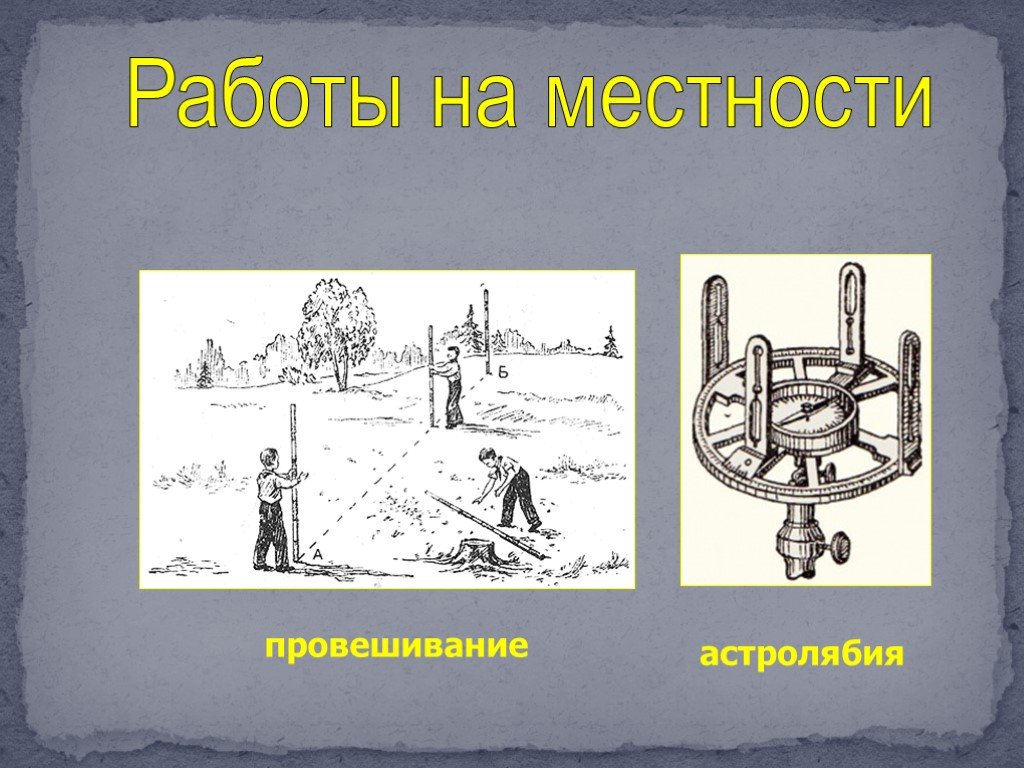
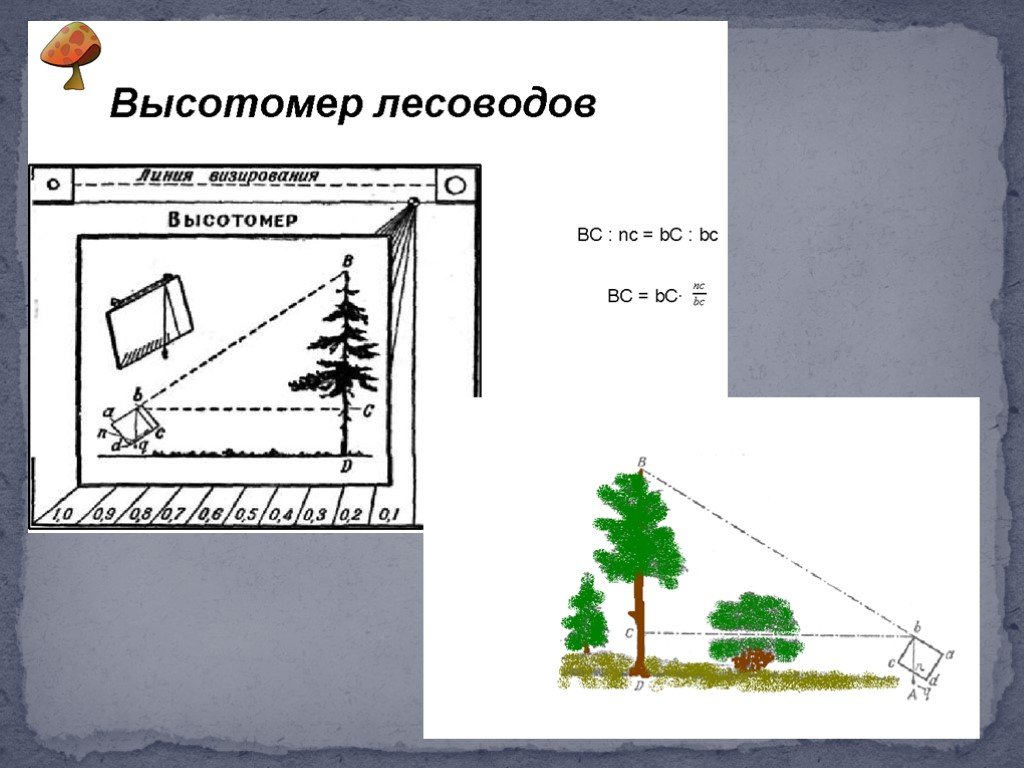
Цель урока:. Закрепить понятие подобия треугольников Узнать где применяется подобие в жизни Рассмотреть решение задач на местности. Понятие подобия ...Применение подобия треугольников
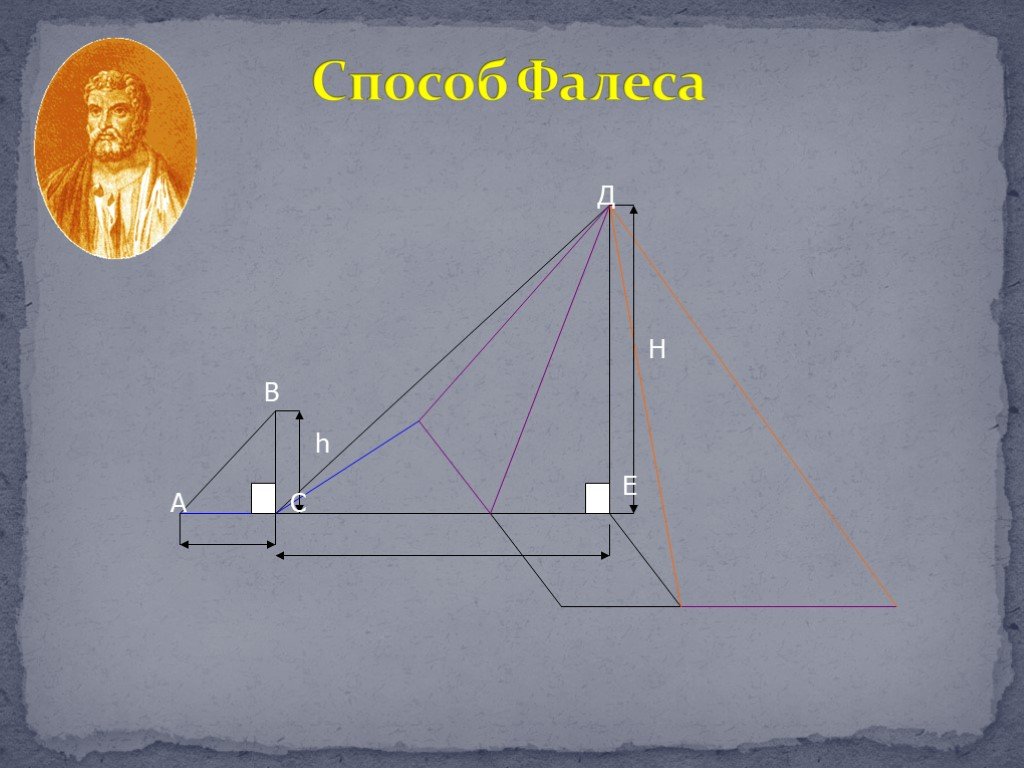
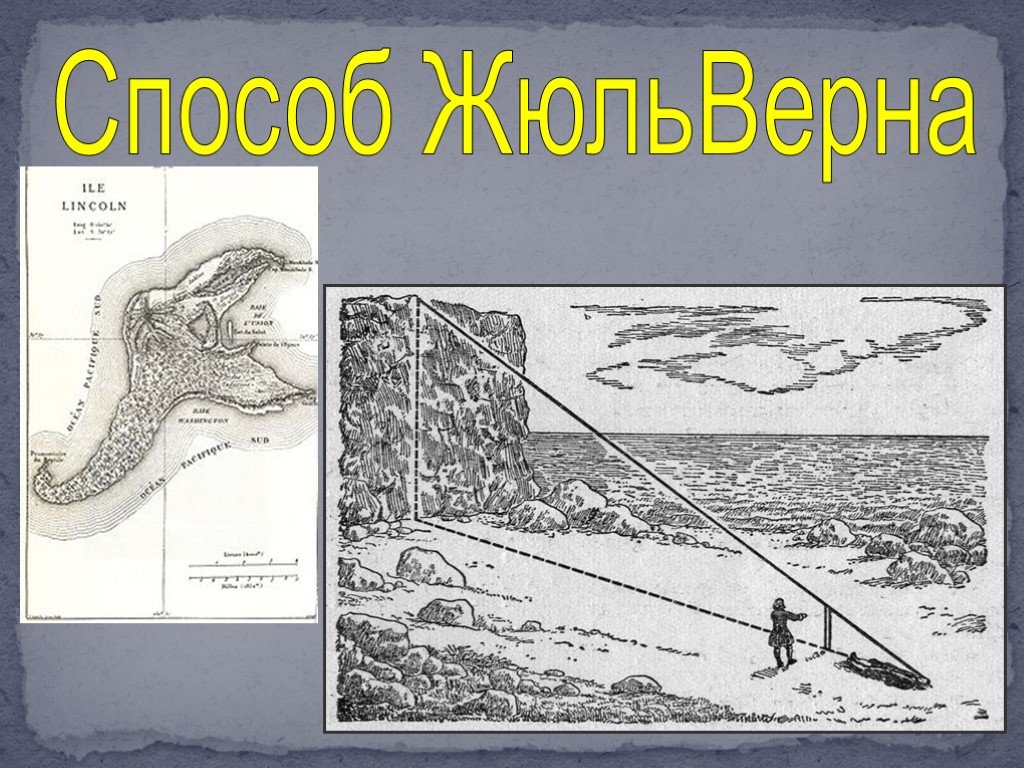
План урока. Применение подобия треугольников при доказательстве теорем. Задачи на построение. Измерительные работы на местности. Применение подобия ...Применение подобия треугольников в жизни
Основополагающий вопрос: «Как и где можно применять признаки подобия треугольников в жизни?» Гипотеза: «Если человек знает признаки подобия треугольников, ...Применение подобия треугольников к решению задач
Применение подобия треугольников к решению задач. Цели урока:. обучающая формировать умения и навыки применения теоретических знаний при решении задач; ...Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников. обобщение и систематизация теоретических знаний по теме «Признаки подобия треугольников» ...Решение задач на применение признаков подобия треугольников
Тема урока. Решение задач на применение признаков подобия треугольников. Цель урока: Обобщение по теме «Признаки подобия треугольников». Задачи урока:. ...Второй и третий признаки подобия треугольников
докажем, что и применим 1 признак подобия треугольников. А С В В1 С1 А1. II признак подобия треугольников. Если две стороны одного треугольника ...Практические приложения подобия треугольников
Аннотация В повседневной жизни нам часто приходится сталкиваться с различными проявлениями подобия, однако подобие в обыденном смысле и с математической ...Практическое применение геометрии
1. Выяснить области применения геометрии в целом. 2. Выяснить области применения теоремы Пифагора. Цель:. Применение геометрии в развед.целях. Измерение ...Практическое применение логарифмов в экономике
Непер Джон (1550 - 1617) Известный английский математик, шотландский барон. Математика и астрономия были его увлечениями, а не профессией. Непер вошел ...Практическое применение производной
ОБУЧАЮЩАЯ :. повторить, обобщить, систематизировать знания по данной теме ; показать учащимся необходимость знания материала изученной темы при решении ...Решение задач на применение свойств подобия
Цель урока: Обобщение по теме «Признаки подобия треугольников». Задачи урока:. Обобщить и систематизировать теоретические знания учащихся; Совершенствовать ...Применение свойств и признаков равенства прямоугольных треугольников к решению практических задач
«Сближение теории с практикой даёт самые благотворные результаты, и не одна только практика от этого выигрывает». П.А. Чебышев. Найдите пары равных ...Решение задач на применение первого признака равенства треугольников
Цель урока. Совершенствование навыков решения задач на применение первого признака равенства треугольников; Закрепление умения доказывать теоремы. ...Признаки равенства и подобия треугольников
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники ...Применение подобия
Company Logo www.themegallery.com Проговор. 1 вариант Определение подобных треугольников. Сформулируйте третий признак подобия треугольников. Сформулируйте ...Задачи на признаки подобия треугольников
- Что есть больше всего на свете? – Пространство. - Что быстрее всего? – Ум. - Что мудрее всего? – Время. - Что приятнее всего? – Достичь желаемого. ...Первый признак подобия треугольников
Цель:. Повторить определение подобных треугольников, теорему об отношении площадей подобных треугольников Рассмотреть первый признак подобия треугольников, ...Конспекты
Практические приложения подобия треугольников
Муниципальное образовательное учреждение. . «Морская кадетская школа им. адмирала Котова П. Г.». Урок по геометрии (8 кл.). Тема: «Практические ...Признаки подобия треугольников
Муниципальное бюджетное общеобразовательное учреждение. «Новомихайловская средняя общеобразовательная школа». Татарского района Новосибирской области. ...Решение задач на применение первого признака равенства треугольников
Конспект урока геометрии в 7 классе. «Решение задач на применение первого признака равенства треугольников». Цель урока. : совершенствование навыков ...Решение задач на применение свойств прямоугольных треугольников
ПЛАН-КОНСПЕКТ УРОКА «Свойства прямоугольных треугольников». . ФИО (полностью). . Павлова Наталья Ивановна. . . . Место работы. ...Применение признаков равенства треугольников к решению задач
b55cb4a895045c55f93796fe95acb7c3.doc. – геометрия 7 класс. . Ладанова И.В. . . МКОУ «Верх-Жилинская ООШ». Косихинский район Алтайский край. ...Решение задач на применение первого признака равенства треугольников
Дата проведения 21.10.2014 г. Урок геометрии в 7 классе. Тема: «Решение задач на применение первого признака равенства треугольников». Цели урока:. ...Масштаб и его практическое применение
Урок в 5-м классе по теме "Масштаб и его практическое применение". . Панфилова Ольга Юрьевна. учитель математики. . . Цели:. . . формировать ...Масштаб: практическое применение
Урок с использованием презентации. Автор: Герасимова Светлана Николаевна (. sn.qer@mail.ru. ). Место работы: муниципальное нетиповое общеобразовательное ...Второй и третий признак подобия треугольников
Урок 35. Второй и третий признак подобия треугольников. Цели урока:. Рассмотреть второй и третий признаки подобия треугольников;. . Показать ...Производные функций и применение производной
Государственное бюджетное общеобразовательное учреждение. . средняя общеобразовательная школа с. Чёрный Ключ. . муниципального района Клявлинский ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:20 сентября 2018
Категория:Математика
Содержит:31 слайд(ов)
Поделись с друзьями:
Скачать презентацию