Презентация "Свойства функции" по математике – проект, доклад
Презентацию на тему "Свойства функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
Свойства и график степенной функции
Г) х3=2-х Ответ:1. д) =1 Ответ:1;-1. Степенные функции, их свойства и графики. Определение: Функции вида y=xr, где r-любое действительное число называют ...Свойства и график функции синус
Устная разминка 1 3 4 5 6 7 8 9 10 11 13 14 15 ☺ cos90° sin90° sin(π/4) cos180° sin270° sin(π/3) cos(π/6) cos360° ctg(π/6) tg(π/4) sin(3π/2) cos(2π) ...Свойства и график функции y=sinx
Свойства функций. Область значений функции. Периодичность. Четность, нечетность. Промежутки знакопостоянства. Промежутки монотонности. Наибольшее ...Свойства и график логарифмической функции
- 5 - 4 - 3 - 2 -1 0 1 2 3 4 5 4 3 2 1 -1 -2 -3 -4. D(f)= E(f)= y=0 при х= y>0 при х y. Логарифмическая функция, её свойства и график. Опр. Логарифмической ...Свойства и график квадратичной функции
Цели:. вспомнить свойства квадратичной функции вспомнить алгоритм построения графика квадратичной функции рассмотреть задания, предлагавшиеся на ГИА. ...Свойства и график показательной функции
Тема: «Свойства и график показательной функции». Цели урока: Усвоить формулировку определения показательной функции; Научиться исследовать показательную ...Понятие предела функции
Определение. Пусть функция f, принимающая действительные значения, определена в некоторой окрестности точки x0, кроме, быть может, самой точки x0. ...Взаимно обратные функции
Цель проекта: Изучить поведение взаимно обратных функций. Установить связь графиков прямой и обратной функций. Подготовиться к успешной сдаче ЕГЭ. ...Понятие линейной функции
Устно:. Является ли линейным заданное уравнение с двумя переменными:. 5х + 3у + 7 = 0 6а – 4в - 1 = 0 5х + 3у = 0. Назовите коэффициенты а, в и с ...Производная функции
Проблемный вопрос. Можно ли находить производные, не используя определение? Существуют ли более удобные способы? Цели и задачи. Научиться находить ...Свойства арифметического квадратного корня
План урока. Организационный момент. Теоретический устный опрос. Расшифруй поговорку. Найди ошибку. Работа в группах. Проблемные ситуации. Итог урока. ...Предел функции в бесконечности и в точке
Число А называется пределом функции у=f(x), при х стремящемся к бесконечности, если для любого, сколь угодно малого числа ε>0, найдется такое положительное ...Применение производной для исследования функции на монотонность и экстремумы
Х У 0 касательная α. k – угловой коэффициент прямой (касательной). Геометрический смысл производной: если к графику функции y = f(x) в точке с абсциссой ...Геометрический смысл производной функции
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н.Крылов. Цель урока. 1) выяснить, в чем состоит геометрический ...График квадратичной функции Неравенства с одной переменной
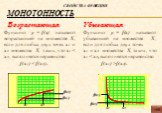
Квадратичная функция и ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая ...Возрастание и убывание функции
Числовые промежутки. [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал. Функция f(x) называется возрастающей на некотором ...Вычисление производной функции
При вычислении производной функции, будем иметь в виду, что один из способов найти производную - это взять достаточно малые значения справа и слева ...Влияние коэффициентов а, b и с на расположение графика квадратной функции
Определите, график какой функции изображен на рисунке:. у = х² – 2х – 1; у = –2х² – 8х; у = х² – 4х – 1; у = 2х² + 8х + 7; у = 2х² – 1. у = ½х² – ...Взаимное расположение графиков линейной функции
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Взаимно обратные функции
Задача. у = f (x), x - ! Найти значение у при заданном значении х. Задача. у = f (x), у- ! Найти значение х при заданном значении у. Дано: у = 2х ...Конспекты
Свойства функции
План – конспект урока в 9 классе на тему «Свойства функции». Учитель математики: Гончарова М.Ф. Дата проведения: 16.12.14. Цели урока:. . . ...Свойства функции
Управление образования г.Астаны. ИПК и ПК СО. ГУ «Средняя школа № 36». Урок алгебры в 10 классе по теме: «Свойства функции». Подготовила: ...Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции
Министерство образования и науки Самарской области. . ГБОУ СПО «Безенчукский аграрный техникум». Конспект занятия. ТЕМА. Предел функции ...Определение числовой функции. Виды. Свойства, графики числовых функций. Способы задания функции
Кейс технологии. Урок алгебры. . Калинина Ирина Борисовна. учитель математики. МАОУ ГИМНАЗИЯ №8 г. Перми. РАЗРАБОТКА УРОКА. c. применением ...Свойства линейной функции
Государственное бюджетное образовательное учреждение. средняя общеобразовательная школа №200 с углубленным изучением финского языка. Красносельского ...Логарифмическая функция. График и свойства логарифмической функции
Класс: 11. Тема урока. : Логарифмическая функция. График и свойства логарифмической функции (Слайд 1,2). Цели урока:. . 1.Ввести определение ...Общее понятие функции, способы её задания, свойства функции
Методическая разработка урока математики по теме. «Общее понятие функции, способы её задания, свойства функции». Пояснительная записка. Преподаватель: ...Свойства показательной функции. Решение показательных уравнений и неравенств
Открытый урок по теме: «Свойства показательной функции. Решение показательных уравнений и неравенств.». Тип урока:. Обобщение и систематизация ...Производная сложной функции
Открытый урок. . по теме: «Производная сложной функции». . . Тип урока:. комбинированный. Цели:. образовательная:. - формирование умения ...Сложение натуральных чисел. Свойства сложения
Конспект. . урока. . разработала. . учитель. . математики. . . . . . Костюкова. . Ольга. . Владимировна. . . Тема урока:. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Шеремета И.В.
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию












![при k < 0 D(f) = (-∞, +∞); Е(f) = (-∞, 0]; четная убывает на луче [0,+∞), возрастает на луче (-∞, 0]; непрерывна; не ограничена снизу, ограничена сверху; унаиб = 0, унаим не существует; y = 0 при х = 0 выпукла вверх. при k > 0 D(f) = (-∞, +∞); E(f) = [0, +∞); четная; убывает на луче (-∞, 0], в при k < 0 D(f) = (-∞, +∞); Е(f) = (-∞, 0]; четная убывает на луче [0,+∞), возрастает на луче (-∞, 0]; непрерывна; не ограничена снизу, ограничена сверху; унаиб = 0, унаим не существует; y = 0 при х = 0 выпукла вверх. при k > 0 D(f) = (-∞, +∞); E(f) = [0, +∞); четная; убывает на луче (-∞, 0], в](https://prezentacii.org/upload/cloud/14/09/6433/images/thumbs/screen12.jpg)


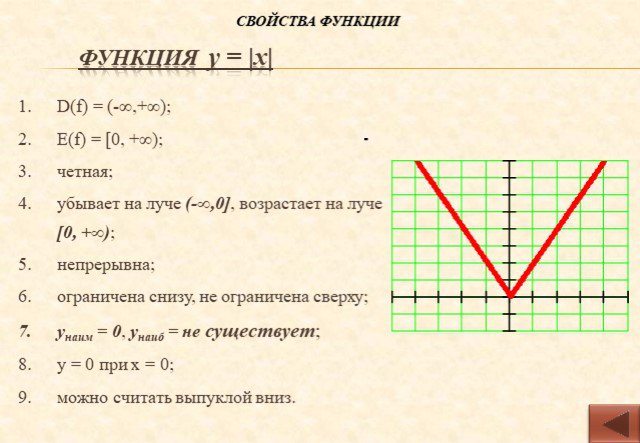
![Функция у = |х|. D(f) = (-∞,+∞); Е(f) = [0, +∞); четная; убывает на луче (-∞,0], возрастает на луче [0, +∞); непрерывна; ограничена снизу, не ограничена сверху; унаим = 0, унаиб = не существует; у = 0 при х = 0; можно считать выпуклой вниз. Функция у = |х|. D(f) = (-∞,+∞); Е(f) = [0, +∞); четная; убывает на луче (-∞,0], возрастает на луче [0, +∞); непрерывна; ограничена снизу, не ограничена сверху; унаим = 0, унаиб = не существует; у = 0 при х = 0; можно считать выпуклой вниз.](https://prezentacii.org/upload/cloud/14/09/6433/images/thumbs/screen15.jpg)
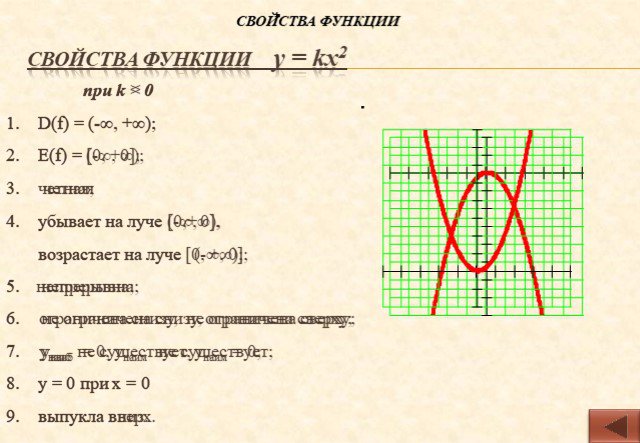
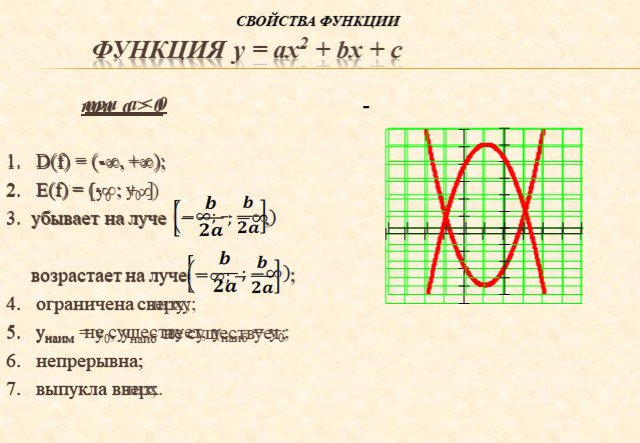
![Функция у = ах2 + bх + с. при а > 0 D(f) = (-∞, +∞); Е(f) = [у0 ; +∞) убывает на луче , возрастает на луче ; ограничена снизу; унаим = у0, унаиб не существует; непрерывна; выпукла вниз; при а < 0 D(f) = (-∞, +∞); Е(f) = (-∞; у0 ] убывает на луче , возрастает на луче ; ограничена сверху; унаим Функция у = ах2 + bх + с. при а > 0 D(f) = (-∞, +∞); Е(f) = [у0 ; +∞) убывает на луче , возрастает на луче ; ограничена снизу; унаим = у0, унаиб не существует; непрерывна; выпукла вниз; при а < 0 D(f) = (-∞, +∞); Е(f) = (-∞; у0 ] убывает на луче , возрастает на луче ; ограничена сверху; унаим](https://prezentacii.org/upload/cloud/14/09/6433/images/thumbs/screen16.jpg)