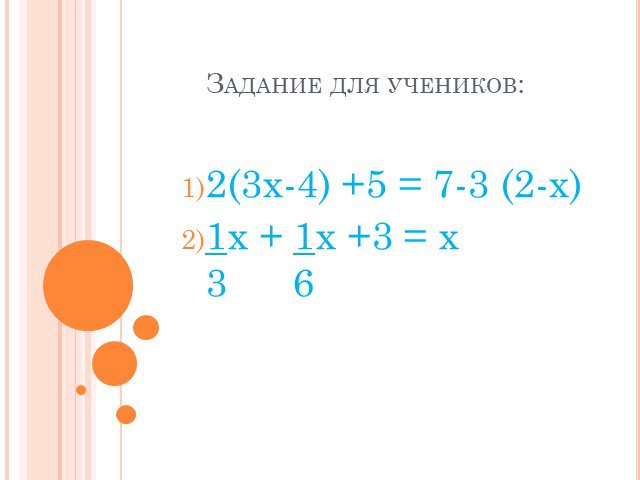Презентация "Рещение линейных уравнений" по математике – проект, доклад
Презентацию на тему "Рещение линейных уравнений" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 11 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение системы линейных уравнений методом Крамера
Системы линейных уравнений. Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных. ...Решение задач с помощью линейных уравнений
1 ряд 2 ряд 3 ряд УСТНАЯ РАБОТА ПРОВЕРЬТЕ! -13 1 19 40 7 4 -5 5 -10 -4 -16 Т 6 14 -36 3 О Л И А Э П К НЕН Р Е Н Г С М Ф. (7х + 1) – (6х + 3)= 5 7х ...Решение систем линейных уравнений
Решение систем линейных уравнений. (урок обобщения). Устная работа. Выразите неизвестное у через х: 2х + у=11; 3х – у=9; 7х=9у; х-у=5; 2х – 2у=6; ...Решение систем линейных уравнений с двумя неизвестными
1. Запишите систему уравнений 5 х – 3 у + 7, х + 2 у = 15. Напишите уравнение, которое получится, если сложить почленно уравнения данной системы. ...Решение систем линейных уравнений для учителя
Общеобразовательное учебное заведение ПМГ математики. Россия, Тольятти 445057, Приморский б-р, 25 Тел. (8482) 34-51-41 Факс (8482) 4074-56. Алгебра ...Решение систем линейных алгебраических уравнений с помощью определителей
Цель:. изучить свойства определителей и применить их в решении систем линейных алгебраических уравнений. Задачи исследования:. рассмотрение схем вычисления ...Решение систем линейных уравнений
1.Что называют системой двух линейных уравнений с двумя переменными? 2.Знак системы? 3.Что называют решением системы двух уравнений с двумя переменными? ...Решение систем двух линейных уравнений с двумя переменными различными способами
Цель урока:. Продолжить формирование навыков сознательного выбора способа решения системы Развивать потребность в нахождении рациональных способов ...Решение нелинейных уравнений
Выбор подходящего метода для решения уравнений зависит от характера рассматриваемой задачи. Задачи, сводящиеся к решению алгебраических и трансцендентных ...Параллельные методы решения систем линейных уравнений
Н.Новгород, 2005 г. Основы параллельных вычислений: Матричное умножение © Гергель В.П. 2 из 44. Постановка задачи Метод Гаусса Последовательный алгоритм ...Решение линейных уравнений с параметрами
Пусть дано уравнение 2х+3=х+а. Здесь х и а – переменные (неизвестные) величины. Переменная а при решении уравнения считается постоянной (т.е. это ...Решение линейных уравнений, с параметрами, содержащими знак модуля
Решить уравнение |х|=а При рассмотрении вариантов для параметра а необходимо помнить, что модуль принимает только неотрицательные значения. при а0 ...Решение линейных уравнений с параметром
Если хочешь строить мост, Наблюдать движенье звезд, Управлять машиной в поле Иль вести машину ввысь, Хорошо работай в школе. Добросовестно учись. ...Решение линейных уравнений
Повторение. 1.Фронтальный опрос правил. 2.Выберите из данных предложенной группы математических записей: а) уравнения; б) Тождества. 1. 5(х-3) 5. ...Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной. Определение. Линейным уравнением с одной переменной называется уравнение вида aх + b = с, где а, в, ...Решение линейных уравнений, содержащих неизвестное под знаком модуля
ЦЕЛЬ РАБОТЫ. Рассмотреть примеры уравнений, содержащих неизвестное под знаком модуля с точки зрения геометрического смысла модуля и алгебраического ...Методы решения систем линейных уравнений 1- ой степени
Проверка домашнего задания. Устная работа. Какие способы решения систем линейных уравнений мы знаем? Сколько их? Какой из способов самый наглядный? ...Методы решения систем линейных уравнений с двумя переменными
Инженер-электрик: "Это уравнения напряжения или токов в электрической цепи с активными сопротивлениями." Инженер-строитель: "Это уравнения, связывающие ...Количество решений систем линейных уравнений с двумя переменными
Цель:. Научиться находить множество решений двух или нескольких линейных уравнений с двумя переменными. Научиться составлять такие системы по заданным ...Метод Гаусса решения систем линейных уравнений
Рассмотрим систему m линейных уравнений с n неизвестными:. Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу, ...Конспекты
Решение задач с помощью систем линейных уравнений
Разработка урока. «Решение задач с помощью систем линейных уравнений». 6 класс. Учитель математики Тансизбаева Г.Н. Задачи урока:. а) ...Решение задач с помощью систем линейных уравнений с двумя переменными
Тема. : Решение задач с помощью систем линейных. . уравнений с двумя переменными. Цель. : создать условия для развития учебно-логических умений ...Решение линейных уравнений с одной переменной
Тема: Решение линейных уравнений с одной переменной. Цель: закрепить навыки решения линейных уравнений с одной переменной. Задачи:. Образовательные:. ...Решение задач с помощью линейных уравнений
Мелентьева Ольга Юрьевна. Шг№22 г. Астана. учитель математики. Тема: Решение задач с помощью линейных уравнений. Тип урока:. объяснение новой ...Решение линейных уравнений
Тема:. Решение линейных уравнений. Урок комплексного применения знаний в 6 классе. Цель урока:. . а). Обучающая – . научить решать задачи, ...Решение линейных уравнений
План-конспект урока по математике "Решение линейных уравнений" 6 класс. Урок с использованием цифровых образовательных ресурсов. . Тема: Решение ...Решение линейных уравнений
Тема урока:. . Решение линейных уравнений. Цель:. Повторить решение линейных уравнений; уравнения с модулем; работу с системой координат. ...Решение линейных уравнений
«. №9 орта мектеп» ММ. ГУ «Средняя школа №9». . Открытый урок по математике в 6 классе по теме:. «Решение линейных уравнений». на городском ...Методы решения систем двух линейных уравнений с двумя переменными
План- конспект урока алгебры в 7 классе по теме: «Методы решения систем двух линейных уравнений с двумя переменными». Орг. момент, сообщение ...Решение квадратных уравнений
Урок для 8 класса по теме «Решение квадратных уравнений». . Цели урока:. образовательные. : обобщение и систематизация основных знаний и умений ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Неизвестен
Содержит:11 слайд(ов)
Поделись с друзьями:
Скачать презентацию