Презентация "Преобразование плоскости" по математике – проект, доклад
Презентацию на тему "Преобразование плоскости" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 29 слайд(ов).
Слайды презентации
Список похожих презентаций
Преобразование графиков функций на координатной плоскости
Эпиграф к уроку. Красота в единстве теории и практики. Цели обучения, воспитания и развития. Рациональные способы построения графиков функций. Развитие ...Преобразование фигур на плоскости. Виды движения
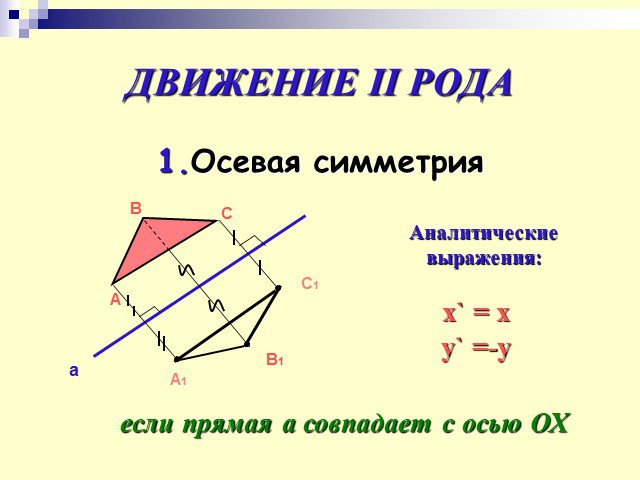
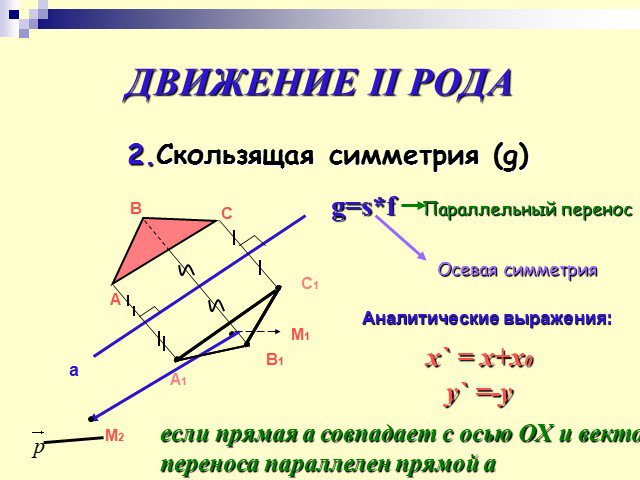
Преобразование плоскости, при котором расстояние между двумя любыми точками сохраняется, называется движением. Из определения следует, что при движении ...Преобразование Наполеоном многоугольников
Содержание: 1. Введение. 2. Преобразование Наполеона треугольников. а) Преобразование Наполеона вложенных фигур. б) Ядро линейного преобразования. ...Преобразование графиков функции
Повторение. Как построить график функции если известен график функции. . Рассмотрим построение графика функции. 1 случай: m – положительное число. ...Преобразование графиков тригонометрических функций
y = cos(x+2) y=cos2x y=sinx +2 y=-3cosx y=sin1/2x y=sin(x-5) y=tg2x y=2ctgx y=ctg1/3x y=1/3sinx y=4-cosx y=ctgx+1. Сгруппируйте функции по какому-нибудь ...Уравнение плоскости в пространстве
Упражнение 1. Дана плоскость: а) 5x-y-1=0; б) 3x+18z-6=0; в) 15x+y-8z+14=0; г) x-3y+15z=0. Назовите координаты вектора нормали. Ответ: а) (5, -1, ...Расстояние от точки до плоскости
N H M a. Определите расстояние от точки М до прямой а. перпендикуляр. Н – основание перпендикуляра. наклонная. N – основание наклонной. HN – проекция ...Проецирование предметов на две и три взаимно перпендикулярные плоскости проекций
Проецирование на одну плоскость. Проецирование на две плоскости. . Проецирование на три плоскости. Найдите соответствие технических рисунков деталей ...Геометрические построения на плоскости
Цель: Исследование роли «геометрического построения на плоскости» в геометрии и архитектуре. Задачи:. 1.Изучить научную литературу, ресурсы сети Интернет ...Взаимное расположение прямых на плоскости
Цели:. Обобщить знания о прямых на плоскости из алгебры и геометрии 7 класса. Выяснить взаимное расположение прямых, заданных уравнением y=kx+b в ...Взаимное расположение прямой и плоскости
1. Прямая принадлежит плоскости. ортогонален нормальному вектору плоскости. И пусть точка. Тогда направляющий вектор прямой. принадлежит прямой. Тогда ...Взаимное расположение прямой и окружности на плоскости
Прямая и окружность пересекаются. d R. d- расстояние от центра окружности до прямой R- радиус окружности. О А В d. Прямая и окружность касаются. d=R. ...Векторы на плоскости
Аналитическая геометрия. Алгебраические поверхности и линии на плоскости первого порядка. Опр. Геометрическое место точек в пространстве (на плоскости) ...Астрономия на координатной плоскости
Цели урока:. Закрепить полученные знания и навыки. Проявить творчество при изучении данного раздела. Избежать трудностей при изучении темы «Функция» ...Преобразование функций
Задачи урока. Повторить правила преобразований:. Построить преобразования тригонометрических функций:. Изучить гармоническую функцию:. Преобразование: ...Преобразование целого выражения в многочлен
Проверка домашнего задания. №975 (а) (х3+7х2+8)+(х2-6х+4)(х-1)= =2х3+10х+4 №981 (в,г) в) 9а2-16ав г) 20х2+24ху №1067 (а(а+2в)+в2)(а(а-2в)+в2)((а2- ...Геометрические фигуры на плоскости
Цели урока. Вспомнить изученные геометрические фигуры и их свойства Убедиться в том, что геометрия не просто школьный предмет, а наука, на которой ...Прямая на плоскости
Цели и задачи. Цели: Рассмотреть основные понятия по теме «Прямая на плоскости» Задачи: Рассмотреть различные способы задания прямой на плоскости ...График функции и его перемещение в координатной плоскости
Определение модуля. Модулем числа называется расстояние от нуля до заданной точки на числовой прямой. | 6 | = 6 | 0 | = 0 | - 6 | = 6 Так как расстояние ...Рисунок на координатной плоскости
Рене Декарт. Декарт Рене (1596-1650) Рене Декарт родился в последний день марта 1596 года в маленьком городке Лаэ провинции Турень, в не очень знатной, ...Конспекты
Преобразование рациональных выражений
1001 идея интересного занятия с детьми. . КОНСПЕКТ УРОКА С ИСПОЛЬЗОВАНИЕМ ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫХ ТЕХНОЛОГИЙ В ОБРАЗОВАНИИ. Барабанова ...Преобразование логарифмических выражений
Урок по теме:. Преобразование логарифмических выражений. Цель: Обобщить и систематизировать знания и умения учащихся применять свойства логарифмов ...Преобразование рациональных выражений
. МБОУ СОШ с углубленным изучением отдельных предметов № 78. . Конспект урока по математике в 8 классе. по теме. . «Преобразование ...Расстояние от точки до плоскости
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа с. Елшанка. Воскресенского района Саратовской области». ...Преобразование дробно-рациональных выражений
Интегрированный урок алгебры и информатики. Тема:. «Преобразование дробно-рациональных выражений. Вставка формул в документ». . Учитель математики. ...Преобразование целого выражения в многочлен
Тема «Преобразование целого выражения в многочлен».7 класс. Цели урока:. - выработать умение применять формулы сокращенного умножения для преобразования ...Преобразование чисел, полученных при измерении
Преобразование чисел, полученных при измерении. 7 класс. . Цели:. Коррекционно-образовательная:. . . Закрепление навыков учащихся в преобразовании ...Перпендикулярность прямой и плоскости
Урок геометрии по теме "Перпендикулярность прямой и плоскости". 10-й класс. Цели:. закрепить вопросы теории по теме «Перпендикулярность прямой ...Построение в координатной плоскости
Муниципальное казенное общеобразовательное учреждение. . «Средняя школа №5» города Михайловска. Методическая разработка урока математики. ...Обобщающий урок. Преобразование выражений, содержащих квадратные корни
Урок алгебры в 8 классе. Тема. : Обобщающий урок. Преобразование выражений, содержащих квадратные корни. Учитель математики. : Байтурова А.Р. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Содержит:29 слайд(ов)
Поделись с друзьями:
Скачать презентацию