Конспект урока «Расстояние от точки до плоскости» по математике для 11 класса
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа с. Елшанка
Воскресенского района Саратовской области»
Конспект урока математики
в 10 классе
«Расстояние от точки до плоскости»
Подготовила
учитель математики
Твёрдая Ирина Александровна
с. Елшанка
2013 год
Тема: расстояние от точки до плоскости.
Тип урока: урок обобщения и систематизации знаний, умений и навыков.
Цели урока.
Дидактические:
– обобщить и систематизировать знания учащихся по теме;
– продолжить формирование умений и навыков по решению задач;
– стимулировать учащихся к овладению решением задач;
– проконтролировать степень усвоения знаний, умений и навыков по теме.
Развивающие:
– совершенствовать, развивать умения и навыки по решению задач на нахождение расстояния от точки до плоскости;
– развивать логическое мышление, учить анализировать и обобщать;
– продолжить работу по развитию математической речи и памяти.
Воспитательные:
– продолжить формирование навыков эстетического оформления записей в тетради и выполнения чертежей;
– приучать к умению общаться и выслушивать других;
– воспитание сознательной дисциплины;
– развитие творческой самостоятельности и инициативы.
| Время (мин.) | Деятельность | ||
| учителя | учащегося | ||
| I. Организационный этап. II. Постановка цели. Сегодня на уроке мы обобщим и систематизируем знания по теме «Расстояние от точки до плоскости», продолжим совершенствовать знания, умения и навыки по теме в ходе решения задач, которые совершенно необходимы каждому ученику, желающему хорошо подготовиться для успешной сдачи ЕГЭ. III. Проверка домашнего задания. На дом вам было предложено решить задачи № 143, № 150. IV. Оперативная диагностика усвоения основных понятий (проводится в виде тестов). V. Решение задач по готовым чертежам. Задача №1(устно)
Дано: АВСД – параллелограмм, ВД, АС – диагонали, АС пересекает ВД в точке О, АМ =МД Доказать: ОМ Задача №2 (устно) Дано: МН Доказать: РК
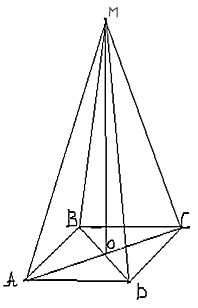
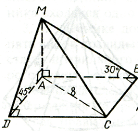
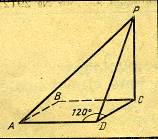
Доказательство: МН – перпендикуляр, МС – наклонная, НС – проекция наклонной МС, РК – прямая, проходящая через основание наклонной НС Следовательно, РК Что и требовалось доказать. Задача №3 (письменно, с записью в тетрадь) Из точки, отстоящей от плоскости на расстоянии 8 см, проведены две наклонные, образующие с плоскостью углы 450, а между собой угол в 600. Найдите расстояние между концами наклонных.
Дано: АА1 прαАВ = А1В;
Найдите ВС. Решение:
следовательно, ВС = АС = АВ = Ответ: ВС = Задача № 4 (из ЕГЭ (приложение № 5)) Рисунок заготовлен на доске. VI. Самостоятельная работа (приложение № 6). Каждому учащемуся выдается лист с заданием, где нужно выделить ручкой с зеленой пастой расстояние от заданной точки к данной плоскости. VII. Домашнее задание. (задачи заранее записаны на доске (приложение № 8)). Задача № 1 Расстояние от точки до плоскости 4треугольника равно а см., а до каждой из его сторон b см. Найдите радиус окружности, вписанной в этот треугольник. Из точки М к плоскости α проведены две наклонные, которые образуют со своими проекциями на плоскость α углы 300. Угол между наклонными равен 900. Найдите расстояние между основаниями наклонных, если расстояние от т. М до плоскости α равно Задача № 3(Из ЕГЭ) Боковое ребро МА пирамиды МАВС перпендикулярно плоскости основания и равно 13,
VIII. Подведение итогов. Выставление отметок за урок. Назначается индивидуальная консультация по устранению пробелов в знаниях по данной теме некоторым учащимся. | 1 3 5 5 3 3 5 8 5 4 3 | (Организационная) Здоровается с детьми. Отмечает готовность класса к уроку (наличие учебных принадлежностей, наличие линейки, простого карандаша и ручки с зеленой пастой). Сообщает тему урока, дату проведения урока, цель урока. (Замечание! Вызывает по желанию, если учащиеся не вызвались показать решение задач, то показывает решение с помощью интерактивной доски. Спрашивает учащихся, какие теоретические сведения были ими использованы при подготовке домашнего задания, и просит дать соответствующие формулировки и пояснения (в случае затруднений некоторых учащихся, совместно с классом проводится коррекция содержания сформировавшихся у них понятий) (приложение № 1, №2)). Выставляет оценки за д/з. Раздает каждому лист с тестом (приложение № 3), проверяет с помощью интерактивной доски. Заполнение производится через копировальную бумагу, оригинал после проверки сдается учителю. Направляет на выбор правильного решения задачи, следит за верностью рассуждений учащихся. Следит за грамотностью построения чертежа и оформления решения задачи. Учащемуся, закончившему решение первым, предлагает оформить его на интерактивной доске. Одновременно проверяет индивидуальные задания, которые выполняются на боковой доске. Обсуждает совместно с учащимися решение задачи, следит за грамотностью рассуждений и верной записью решения. Следит за выполнением самостоятельной работы. Проверка осуществляется с помощью интерактивной доски. Подводит итог результатов самостоятельной работы вместе с ребятами. Помогает в выполнении задания слабым учащимся, если это требуется. Оценивает их. Поясняет домашнее задание, обращая внимание учащихся на то, что аналогичные задания были разобраны на уроке. Над заданием № 3 нужно будет подумать: какие дополнительные построения нужно выполнить, чтобы показать расстояние от точки А до плоскости ВСМ. Задание № 3 выполнять необязательно, им можно заменить любое из заданий №1 или №2, но за него будет выставляться оценка в журнал. Выясняет наличие вопросов, которые появились при решении рассмотренных на уроке задач, а так же просит ребят оценить свою работу на уроке, на сколько она была плодотворной. Что было на уроке удачным, что нет. | Перед уроком староста класса кладет на стол учителя дневник посещаемости, в котором указаны отсутствующие. Записывают в тетради. 2 человека дома оформляли решение задач на слайдах. Комментируют решение задач и отвечают на вопросы учителя. Все остальные слушают, поправляют, дополняют ответы отвечающих. Рассаживаются по одному и выполняют тесты каждый индивидуально, проверку выполняют сами зеленой пастой: против правильного ответа ставится «+», неправильного « – ». Оценивают себя сами. Наносят данные в задаче на рисунок. Один учащийся объясняет устно решение задачи, все остальные поправляют и дополняют отвечающего (если есть в этом необходимость). Устно разбирают решение задачи, затем самостоятельно оформляют ее решение в тетрадях. Ему нужно сориентироваться и заполнить пропуски в заготовленном за шторкой решении. Параллельно 3 человека выполняют индивидуальные задания на доске (приложение № 4) Один ученик решает у доски, остальные записывают решение в тетрадях. Каждый работает самостоятельно, показывает нужное расстояние зеленым цветом, а проверяет красным и ставит себе оценку. Одновременно по карточкам работают двое слабых учащихся (приложение №7) Один выполняет задание на интерактивной доске, другой на боковой. Внимательно прослушав пояснение учителя, записывают домашнее задание. Оценивают работу каждого и работу класса в целом. Отмечают положительные и отрицательные стороны урока (если таковые, по их мнению, имеются). |
![]()
Приложение №1.
Задача №143
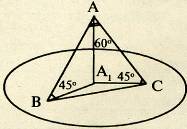
Расстояние от точки М до каждой из вершин правильного треугольника АВС равно 4 см . Найдите расстояние от точки М до плоскости АВС, если АВ = 6 см .
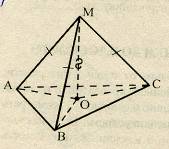
Решение.
Опустим перпендикуляр МО к плоскости (АВС).
1. МО![]() (АВС).
(АВС).
2. ∆ АОМ = ∆ ВОМ = ∆ СОМ (как прямоугольные по гипотенузе и катету) ![]() АО = ВО = СО, т.е. О – центр описанной около ∆ АВС окружности.
АО = ВО = СО, т.е. О – центр описанной около ∆ АВС окружности.
3. R = ![]() , R =
, R = ![]() = 2
= 2![]() см.
см.
4. ∆ МОС – прямоугольный, МО = ![]() =2 см.
=2 см.
Ответ: 2 см .
Задача № 150.
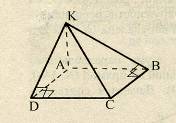 Дано: ABCD – прямоугольник, АК
Дано: ABCD – прямоугольник, АК ![]() (ABC),
(ABC),
KD = 6 см., КВ = 7 см., КС = 9 см.
Найдите ρ (К, (АВС)), ρ (АК, CD).
Решение.
1. ρ (К, (АВС)) = АК.
| | |
| АВ |
|
| АВ – проекция | |
| КВ - наклонная | |
3. ∆ КВС – прямоугольный. СВ = ![]() см.
см.
4. ∆ АКД – прямоугольный. АК = ![]() см.
см.
5. ρ (АК, CD) = AD; AD = ![]() см.
см.
Ответ: 2 см.; ![]() см.
см.
Приложение № 2.
| Формулировка | |
| 1. Расстояние между точками. 2. Расстояние от точки до плоскости. 3. Свойство точки равноудаленной от вершин многоугольника. 4. Расстояние между скрещивающимися прямыми. 5.Общий перпендикуляр двух скрещивающихся прямых. | Расстояние между точками – длина отрезка, соединяющего их. Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из данной точки на плоскость. Точка равноудаленная от всех вершин многоугольника является центром описанной около многоугольника окружности. Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них. |
Приложение № 3.
Тест по теме «Расстояние от точки до плоскости».
1.Отрезок АН называется__перпендикуляром___________________,
проведенным из точки А к плоскости ![]() , если прямая АН
, если прямая АН ![]()
![]() и пересекает ее в точке Н. Точка Н – основание перпендикуляра______________________
и пересекает ее в точке Н. Точка Н – основание перпендикуляра______________________
2.Отрезок АМ называется __наклонной___________________________,
проведенной из точки А к плоскости ![]() , если прямая АМ не перпендикулярна плоскости
, если прямая АМ не перпендикулярна плоскости ![]() и пересекает ее в точке М. Точка М – ___основание наклонной_
и пересекает ее в точке М. Точка М – ___основание наклонной_
3. Перпендикуляр, проведенный из данной точки к плоскости, __меньше__________любой наклонной, проведенной из той же точки к этой плоскости.
4. Длина перпендикуляра, проведенного из точки А к плоскости ![]() называется _расстоянием от точки А к плоскости
называется _расстоянием от точки А к плоскости![]() _________________
_________________
5. Через точку М проведены прямые c и d , пересекающие плоскость ![]() в точках С и Д, причем прямая с
в точках С и Д, причем прямая с ![]()
![]() . Тогда МС – _перпендикуляр______, МД – _____наклонная__________, СД – __проекция наклонной____________
. Тогда МС – _перпендикуляр______, МД – _____наклонная__________, СД – __проекция наклонной____________
6. Расстояние от точки А до плоскости ![]() равно 3 см. Длина перпендикуляра, проведенного из точки А к плоскости
равно 3 см. Длина перпендикуляра, проведенного из точки А к плоскости ![]() равно _____3 см________.
равно _____3 см________.
7. Установите соответствие по рисунку.
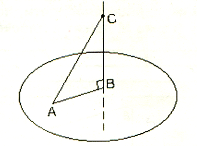
1. АС А. Проекция наклонной.
2. СВ В. Перпендикуляр.
3. АВ С. Наклонная.
Ответ: 1 __С__ 2 __В___ 3 ___А___
8. Из точки А к плоскости ![]() проведены наклонная АВ длиной 5 см. Найдите ее проекцию, если расстояние от точки до плоскости 3 см.
проведены наклонная АВ длиной 5 см. Найдите ее проекцию, если расстояние от точки до плоскости 3 см.
Ответ: _4 см.____
9. Расстояние между параллельными плоскостями – это расстояние _____расстояние от точки одной плоскости до другой_____________
10. Расстоянием между скрещивающимися прямыми называют __длину их общего перпендикуляра___________________________
11. Прямая NM параллельна плоскости ![]() . Расстоянием от точки N до плоскости
. Расстоянием от точки N до плоскости ![]() равно 6 см. Расстояние от точки М до плоскости равно _ 6 см__
равно 6 см. Расстояние от точки М до плоскости равно _ 6 см__
12. Точка В лежит в плоскости ![]() , а точка А находится от плоскости на расстоянии 8 см. Найдите расстояние от середины отрезка АВ до плоскости
, а точка А находится от плоскости на расстоянии 8 см. Найдите расстояние от середины отрезка АВ до плоскости ![]() .
.
Ответ: 4 см.
Приложение № 4
Карточка № 1
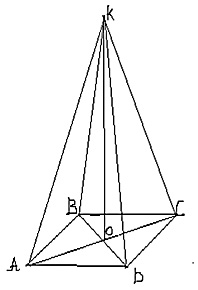
Дано:
АВСD – квадрат, ОК ![]() (АВС),
(АВС),
ОК=4см, DС= 3![]() см
см
Найти: АК, ВК, СК, DК.
Решение:
1) ВD![]() АС
АС
DC = ![]()
![]() ОС2 =
ОС2 = ![]() =
=![]() = 9
= 9 ![]() ОС = 3 см.
ОС = 3 см.
2) ∆ КОС – прямоугольный (КО![]() (АВС))
(АВС)) ![]() КС=
КС=![]() =
= ![]() = 5см.
= 5см.
3) АК = ВК = СК = DК = 5 см. (равные наклонные равных проекций, ОА = ОD = ОС = АО, т.к. АВСD – квадрат, АС = ВD, О – точка пересечения диагоналей).
Ответ: АК = ВК = СК = DК = 5 см.
Карточка № 2
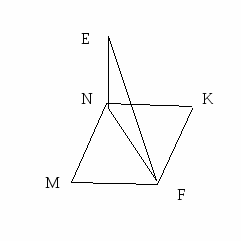
Пользуясь рисунком, на котором изображен квадрат MNKF, найдите расстояние от точки Е до плоскости (MNKF), если MN =4 см., EF = 12 см., EN ![]() (MNKF).
(MNKF).
Решение:
-
NF =
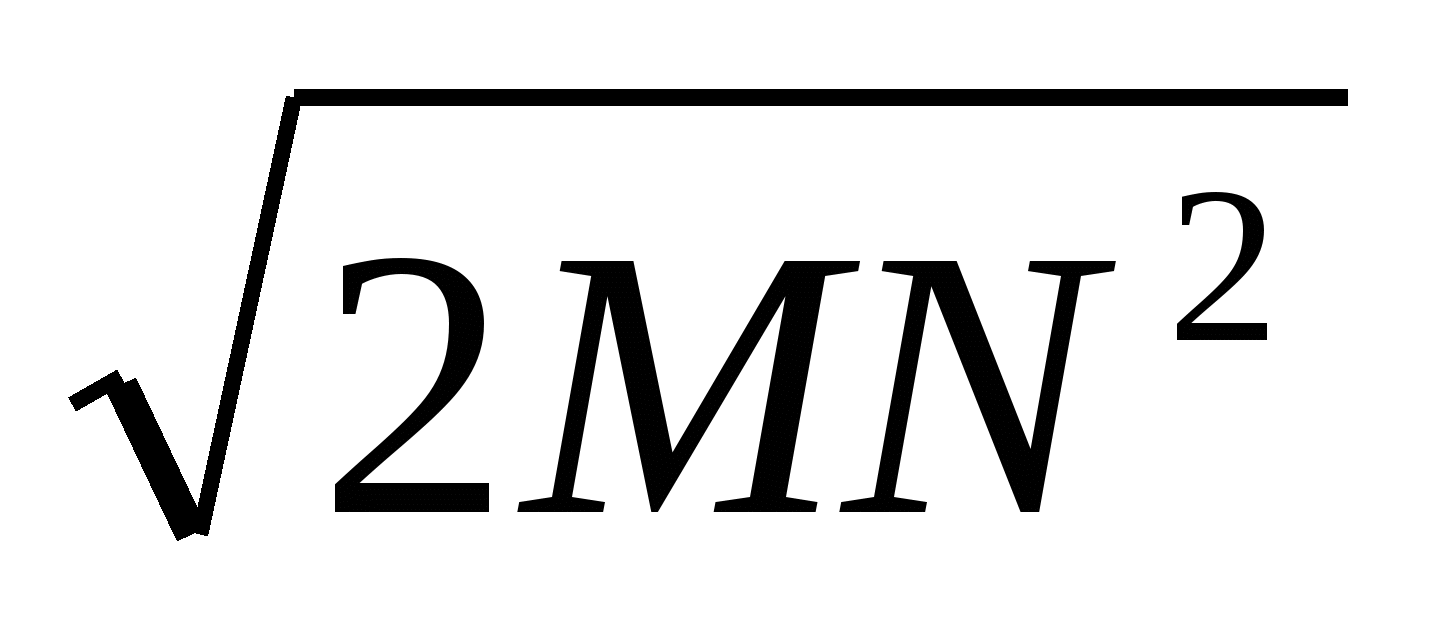 =
= 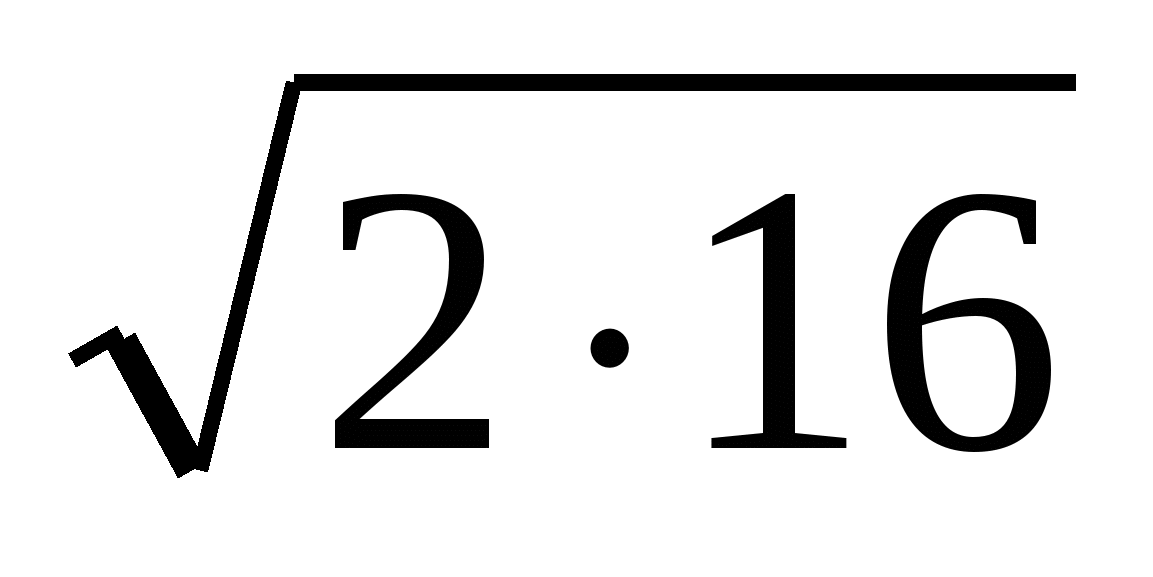 =
=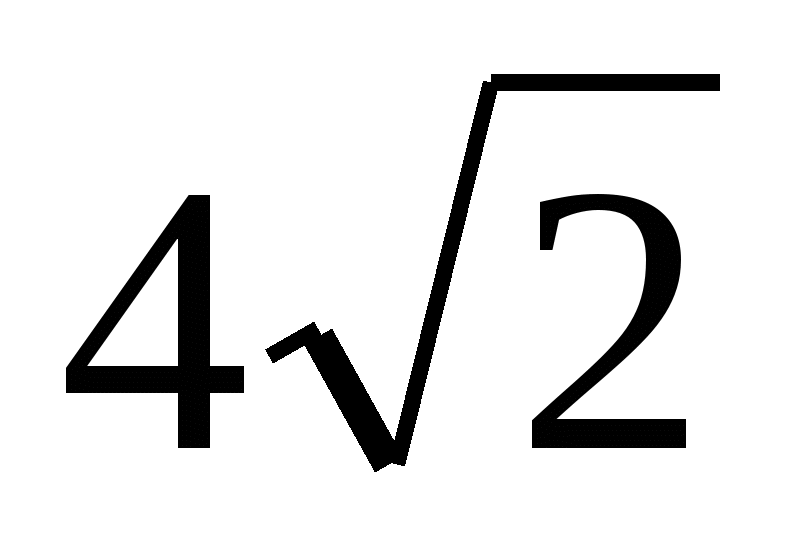 cм.
cм. -
EN
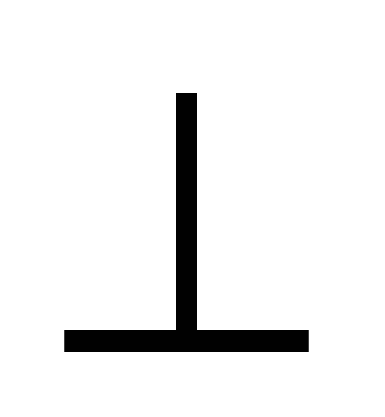 (MNKF)
(MNKF)  EN
EN 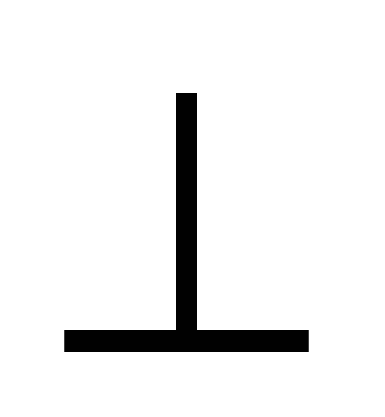 NF
NF  ∆ENF – прямоугольный.
∆ENF – прямоугольный.
EN = ![]() =
=![]() =
=![]() =
=![]() см.
см.
Ответ: EN = ![]() см.
см.
Карточка № 3
И з точки А, удаленной от плоскости γ на расстояние d, проведены наклонные АВ и АС под углом 300 к этой плоскости. Их проекции на плоскость γ образуют угол в 1200.
з точки А, удаленной от плоскости γ на расстояние d, проведены наклонные АВ и АС под углом 300 к этой плоскости. Их проекции на плоскость γ образуют угол в 1200.
Найдите ВС.
Решение:
-
Из ∆ АОВ:
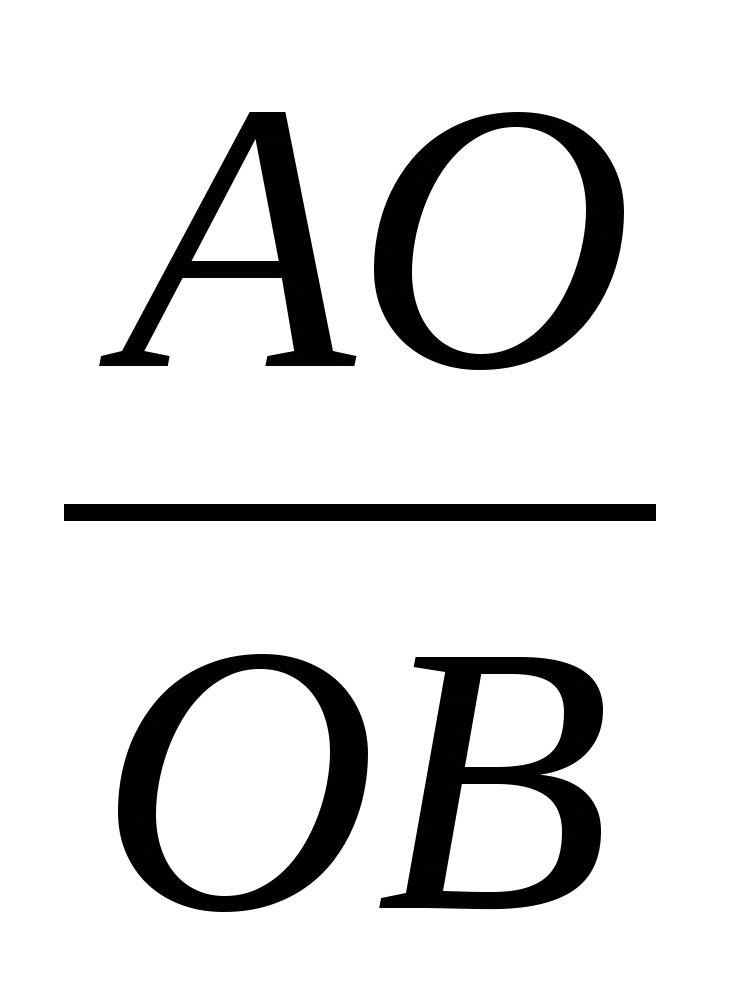 = tg300, ОВ = d·
= tg300, ОВ = d·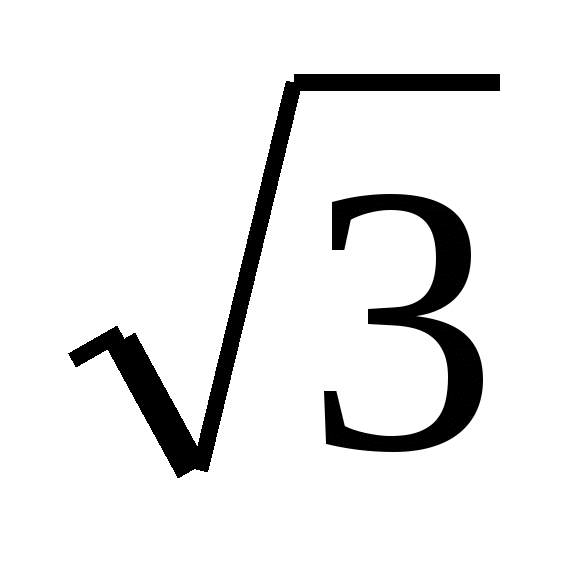
-
ОВ = ОС.
-
Из ∆ ВОС по теореме косинусов:
ВС2 = ОВ2 + ОС2 – 2 · ОВ · ОС · cos1200,
ВС2 = 3d2 + 3d2 – 2 · d·![]() · d·
· d·![]() ·
·![]() ,
,
ВС2 = 9d2, ВС = 3d.
Ответ: ВС = 3d.
Приложение № 5
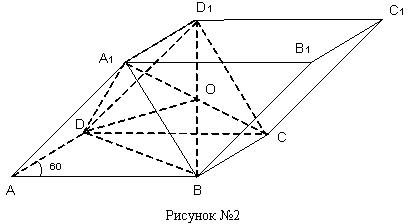 С3 из варианта №34 ЕГЭ 2004г
С3 из варианта №34 ЕГЭ 2004г
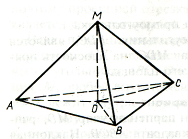
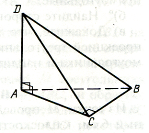
Все грани призмы АВСDA1B1C1D1 – равные ромбы со стороной, равной 4. Углы BAD, BAA1 и DAA1 равны 60° каждый. Найдите расстояние от точки D до плоскости BCD1.
Решение задачи:
Призма эта – параллелепипед, так как все грани являются параллелограммами. Докажем, что DO – искомое расстояние.
∆BAD - равнобедренный с углом при вершине 60°, следовательно, углы при основании тоже по 60°; получаем, что ∆ BAD – равносторонний, BD = 4.
Аналогично, рассмотрев треугольники ∆A1AD и ∆A1AB, приходим к выводу:
DA1 = 4, A1B = 4.
BA1D1C – параллелограмм (BC || A1D1 и BC = A1D1), в котором BD1 и A1C – диагонали, следовательно, они точкой пересечения делятся пополам.
∆CDA1 – равнобедренный (DA1 = 4; CD = 4); DO – медиана и, следовательно, высота, т.е. DO![]() A1C , аналогично в ∆ BDD1 DO
A1C , аналогично в ∆ BDD1 DO![]() BD1
BD1
По признаку перпендикулярности прямой и плоскости DO ![]() (BCD1) и DO – искомое расстояние.
(BCD1) и DO – искомое расстояние.
Длину отрезка DO находим как катет прямоугольного треугольника ∆DOB с гипотенузой DB = 4 и катетом BO. Находим BO как радиус окружности, описанной около квадрата
BA1D1C со стороной а = 4 по формуле R = ![]() , предварительно доказав, что параллелограмм BA1D1C является квадратом (BO=OD1=OA1=OC, как проекции равных наклонных DB=DD1=DA1=DC = 4, и стороны параллелограмма BA1=A1D1=D1C=BC= 4).
, предварительно доказав, что параллелограмм BA1D1C является квадратом (BO=OD1=OA1=OC, как проекции равных наклонных DB=DD1=DA1=DC = 4, и стороны параллелограмма BA1=A1D1=D1C=BC= 4).
∆DOB: ![]() DOB = 90°, DB = 4, BO =
DOB = 90°, DB = 4, BO =![]() по теореме Пифагора DO =
по теореме Пифагора DO = ![]() Ответ:
Ответ: ![]()
Приложение № 6
Показать на рисунке расстояние от данной точки до заданной плоскости.
| ρ (М,(АВС)) | |
|
| ρ (D,(АВС)) |
|
| ρ (М,(АВСD)) |
|
| ρ (M,(АВСD)) |
|
| ρ (M,(АВС)) |
|
| ρ (P,(АВСD)) |
Приложение № 7
Карточка №1
Проделайте предложенные операции, впишите необходимые данные и сделайте вывод.
а) Поставьте на плоскости α точку О, обозначая кратчайшее расстояние от точки А до плоскости.
АО_________плоскости α; точка О - _______________ перпендикуляра.
б) Обозначьте другие точки В, С, D, К. Сравните длину прямых АВ, АС, АК, АD с длиной АО.
АВ ______ АО, АС ______АО,
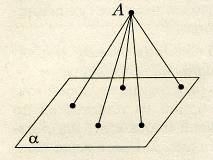
АК _______АО, АD_______АО.
Прямые АВ, АС, АК, АD и т.д. называются наклонными, их из точки А можно провести _____
Точки В, С, К, D – основания наклонных.
ВО – проекция наклонной АВ;
СО - ___________________________________________________;
DО - ___________________________________________________;
КО - ___________________________________________________.
Карточка №2
Закончите фразы в предложенном рассуждении, чтобы оно получилось верным:
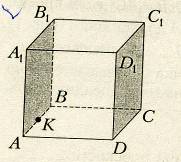
а) Расстояние между параллельными плоскостями - это расстояние от любой точки одной из плоскостей до другой плоскости. Рассмотрите рисунок. Расстояние между выделенными плоскостями – это отрезки ________________________________.
б) Расстояние от точки К до плоскости DD1C1C: ______________________________________.
в) Расстояние от точки А до плоскости А1В1С1D1: ______________________________________________________________.
Приложение № 8
Задача № 1
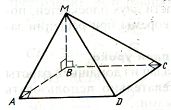
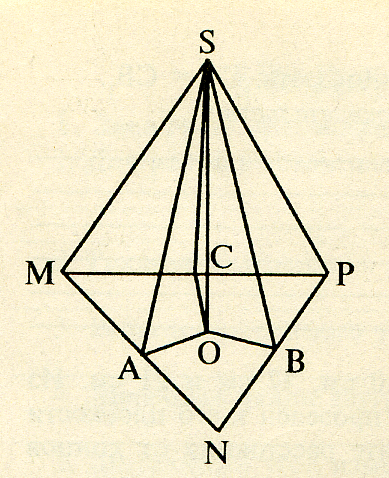 Расстояние от точки до плоскости треугольника равно а см., а до каждой из его сторон b см. Найдите радиус окружности, вписанной в этот треугольник.
Расстояние от точки до плоскости треугольника равно а см., а до каждой из его сторон b см. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
-
т.к. SA
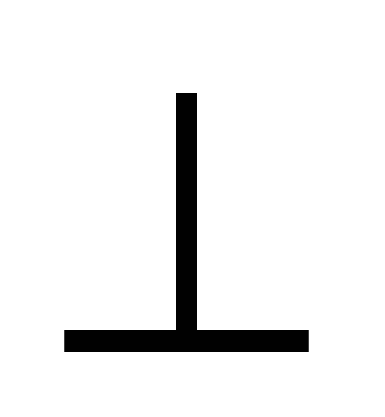 MN, SC
MN, SC 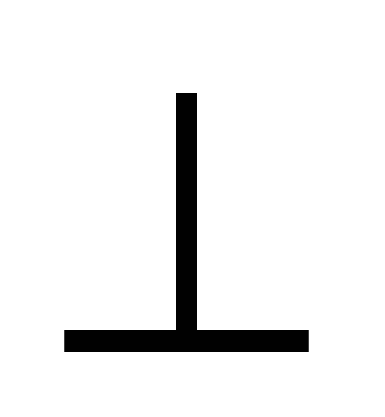 MP и SB
MP и SB 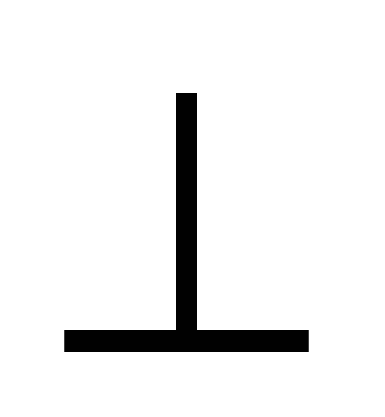 NP (по условию) и SA=SC=SB= а (см), то т. О – точка пересечения серединных перпендикуляров ∆ MNP.
NP (по условию) и SA=SC=SB= а (см), то т. О – точка пересечения серединных перпендикуляров ∆ MNP. -
SO
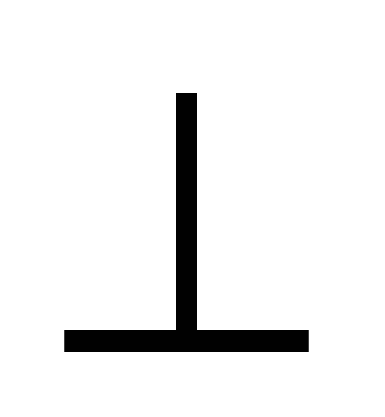 MNP, следовательно, SO
MNP, следовательно, SO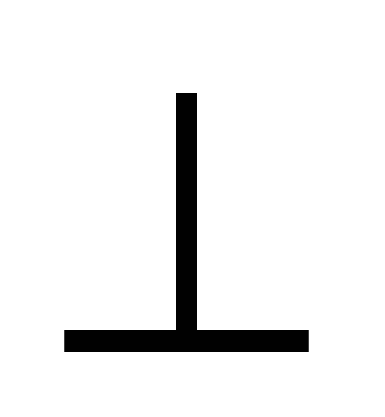 АО, SO
АО, SO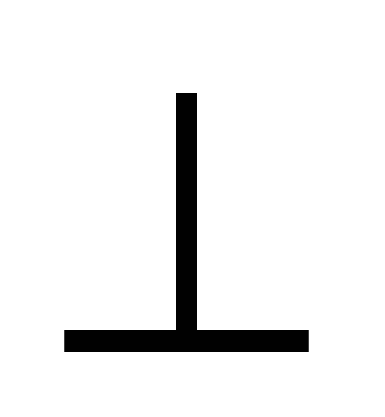 ОС и SO
ОС и SO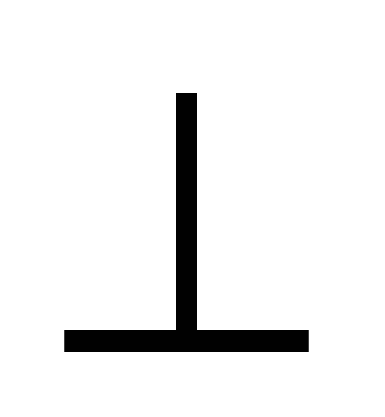 ОВ (по _________
ОВ (по _________
_________________________________)
∆ SOА = ∆ SOВ = ∆ SOС (по ___________________________________)
-
АО =
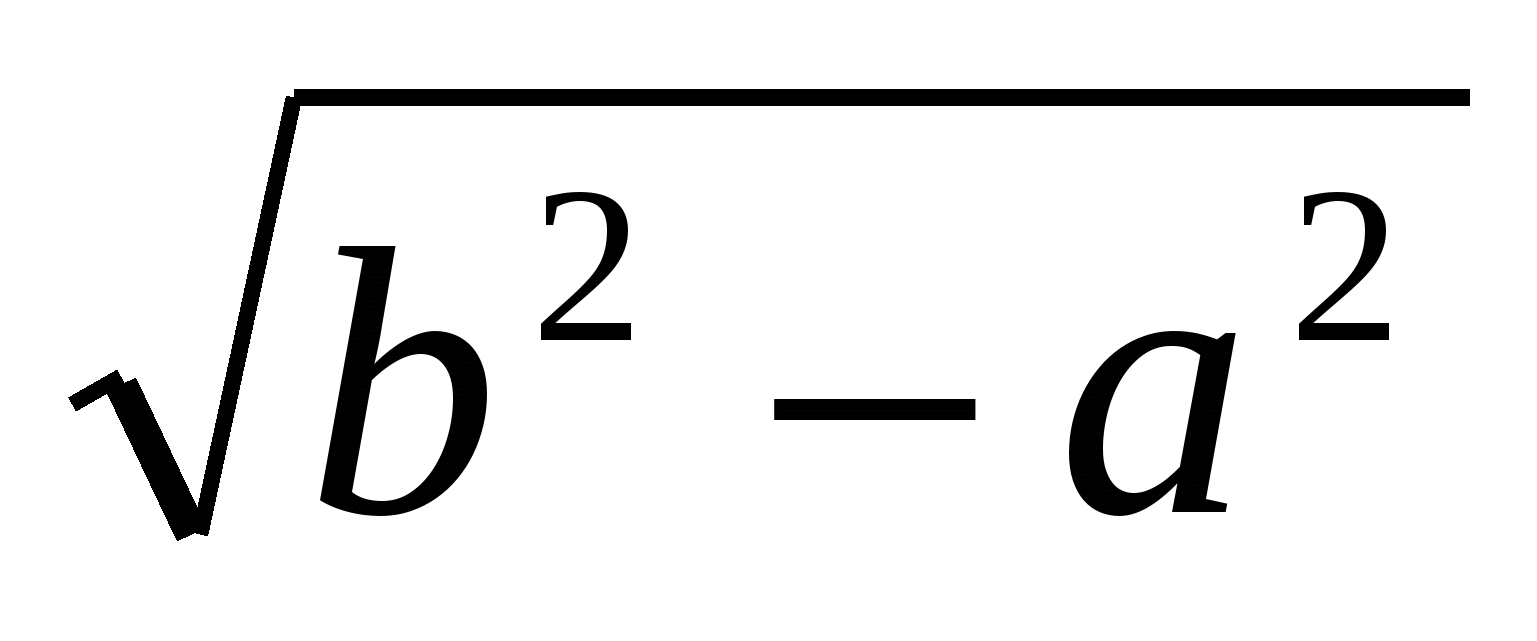 .
.
Ответ: ![]() .
.
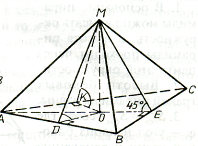
Задача № 2
Из точки М к плоскости α проведены две наклонные, которые образуют со своими проекциями на плоскость α углы 300. Угол между наклонными равен 900. Найдите расстояние между основаниями наклонных, если расстояние от т. М до плоскости α равно ![]() см.
см.
![]() ВМС = 900,
ВМС = 900,
МА![]() α, МА =
α, МА = ![]() см.
см.
Решение:
-
∆АМВ = ∆СМА (по катету и острому углу: катет МА – общий,
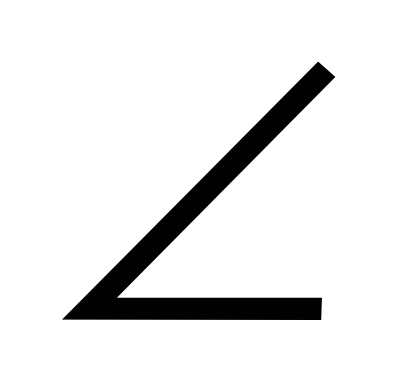 МВА=
МВА= 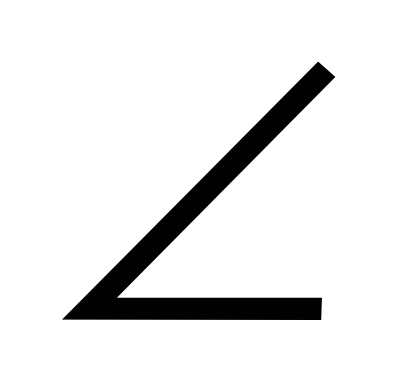 МСА по условию) Значит, ВМ = МС = 2
МСА по условию) Значит, ВМ = МС = 2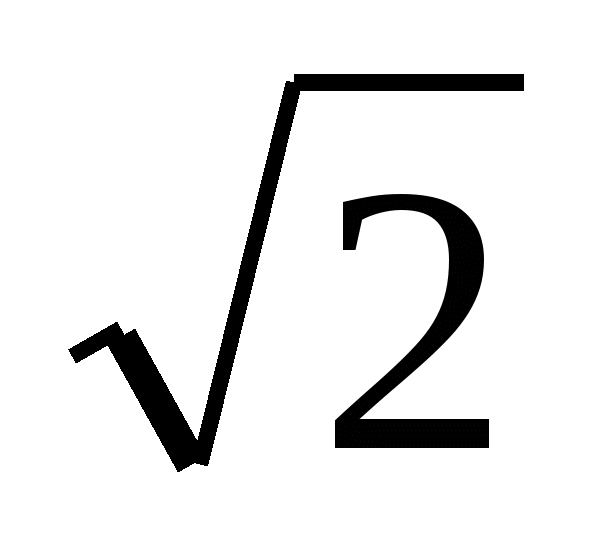 см. (по свойству катета, лежащего против угла в 300)
см. (по свойству катета, лежащего против угла в 300) -
∆ВМС – прямоугольный, равнобедренный:
 ВМС = 900, ВМ = МС. Значит, ВС =
ВМС = 900, ВМ = МС. Значит, ВС = 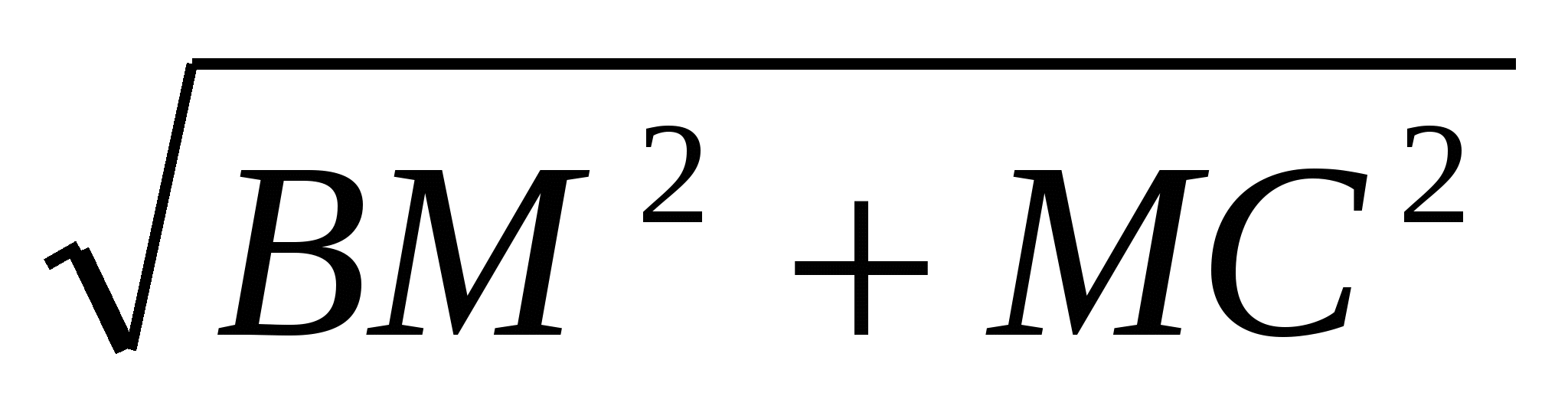 =
=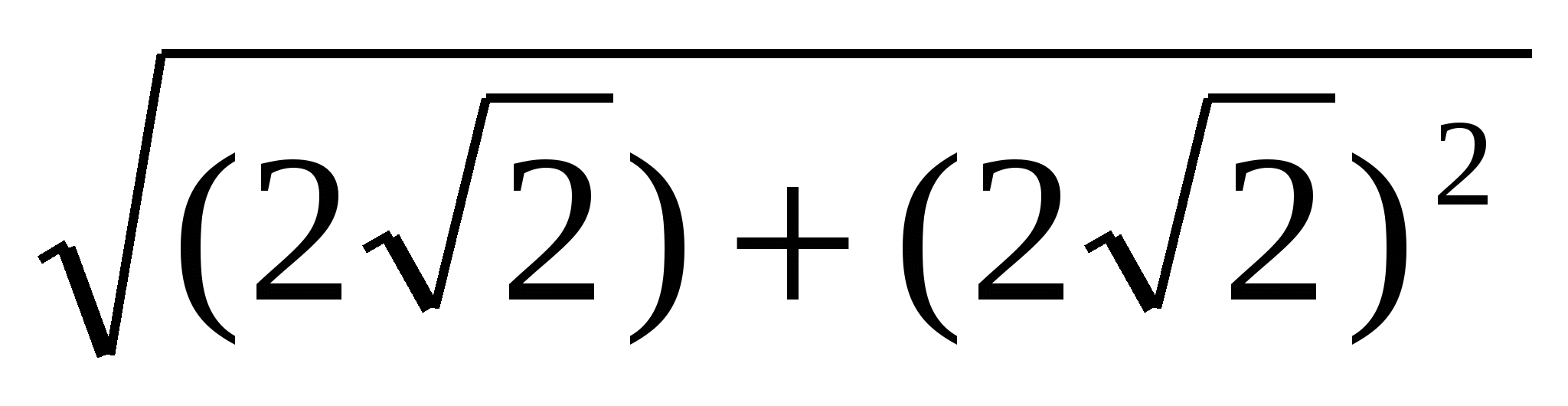 =4 см.
=4 см.
Ответ: 4 см.
Задача № 3(Из ЕГЭ)
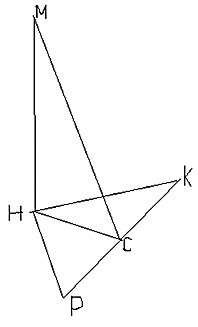
Боковое ребро МА пирамиды МАВС перпендикулярно плоскости основания и равно 13, ![]() ВАС = 900, АВ = 39 и АС = 52. Найдите расстояние от вершины А до плоскости ВСМ.
ВАС = 900, АВ = 39 и АС = 52. Найдите расстояние от вершины А до плоскости ВСМ.
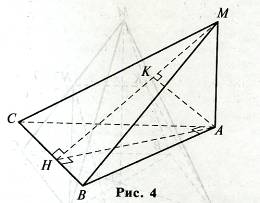
Решение:
Если через точку А провести плоскость, перпендикулярную плоскости ВСМ, то перпендикуляр, проведенный через точку А к линии пересечения этих плоскостей, будет перпендикуляром и к плоскости ВСМ.
Пусть АН ![]() ВС, тогда по теореме о трех перпендикулярах МН
ВС, тогда по теореме о трех перпендикулярах МН ![]() ВС. Следовательно, ВС
ВС. Следовательно, ВС![]() АМН и МВС
АМН и МВС![]() АМН. Проведем в плоскости АМН перпендикуляр АК к прямой МН. Тогда АК
АМН. Проведем в плоскости АМН перпендикуляр АК к прямой МН. Тогда АК![]() ВСМ. Длина отрезка АК равна расстоянию от точки А до плоскости ВСМ.
ВСМ. Длина отрезка АК равна расстоянию от точки А до плоскости ВСМ.
В треугольнике АВС: ВС = ![]() = 65.
= 65.
Поскольку 2SАВС= 39 · 52 = 65 · АН, значит, АН = ![]()
![]() .
.
В треугольнике АМН: МН = ![]() .
.
Поскольку 2SАМН = 13·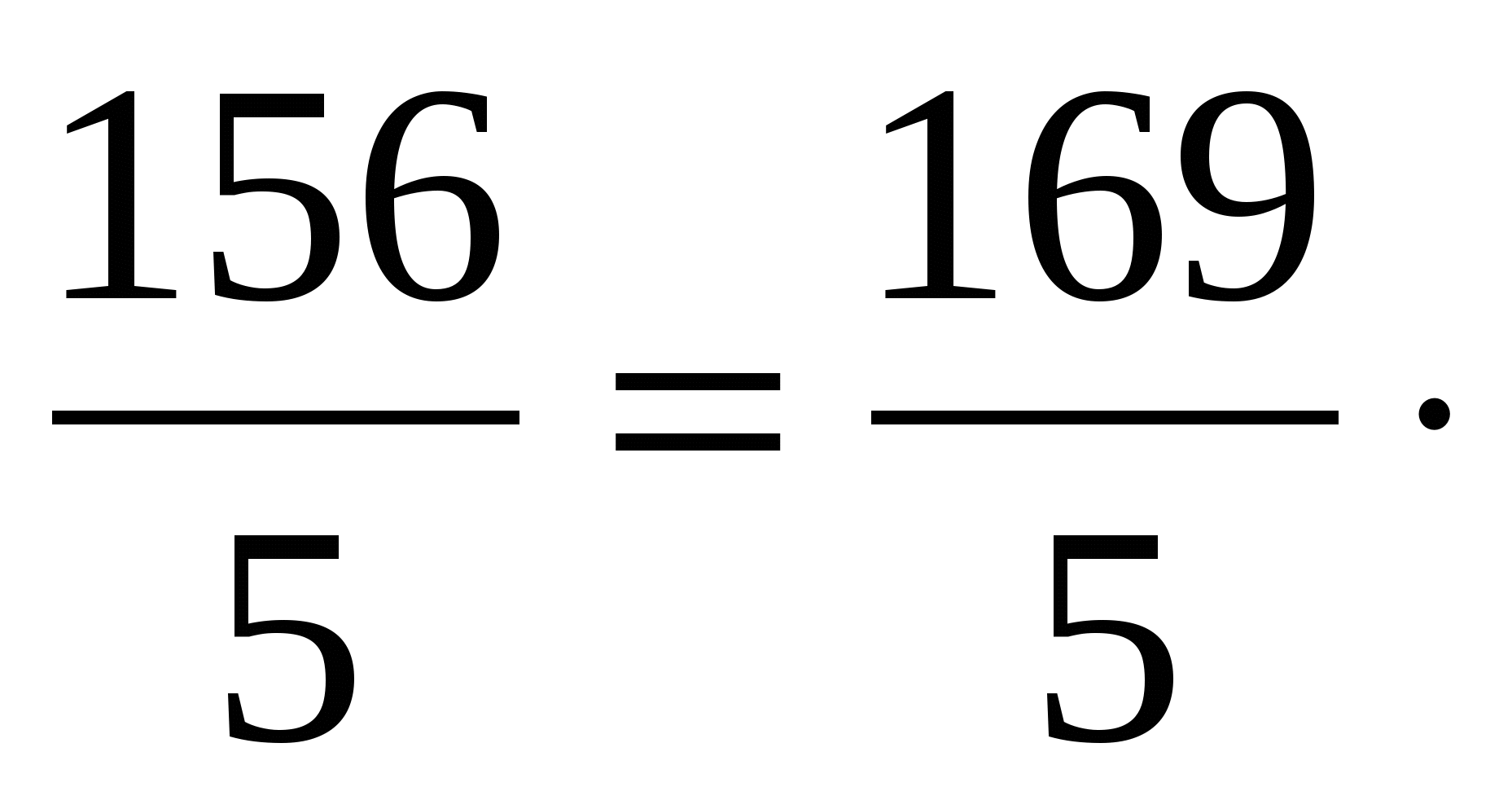 АК, то АК =
АК, то АК = ![]() =12.
=12.
Ответ: 12.
Список использованной литературы.
-
Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.. Геометрия. 10-11 класс. М.: Просвещение, 2009 г.
-
Т.Н. Алешина. Обучающие и проверочные задания. Геометрия 10 класс. М: Интеллект – Центр. 1998г.
Здесь представлен конспект к уроку на тему «Расстояние от точки до плоскости», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.