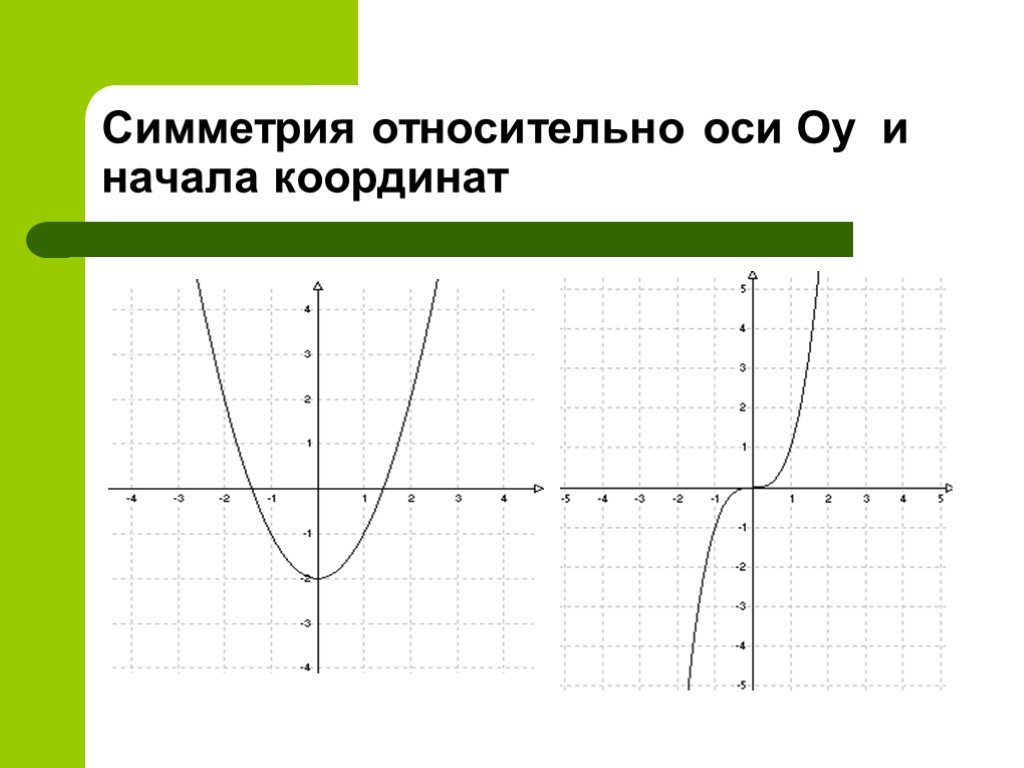
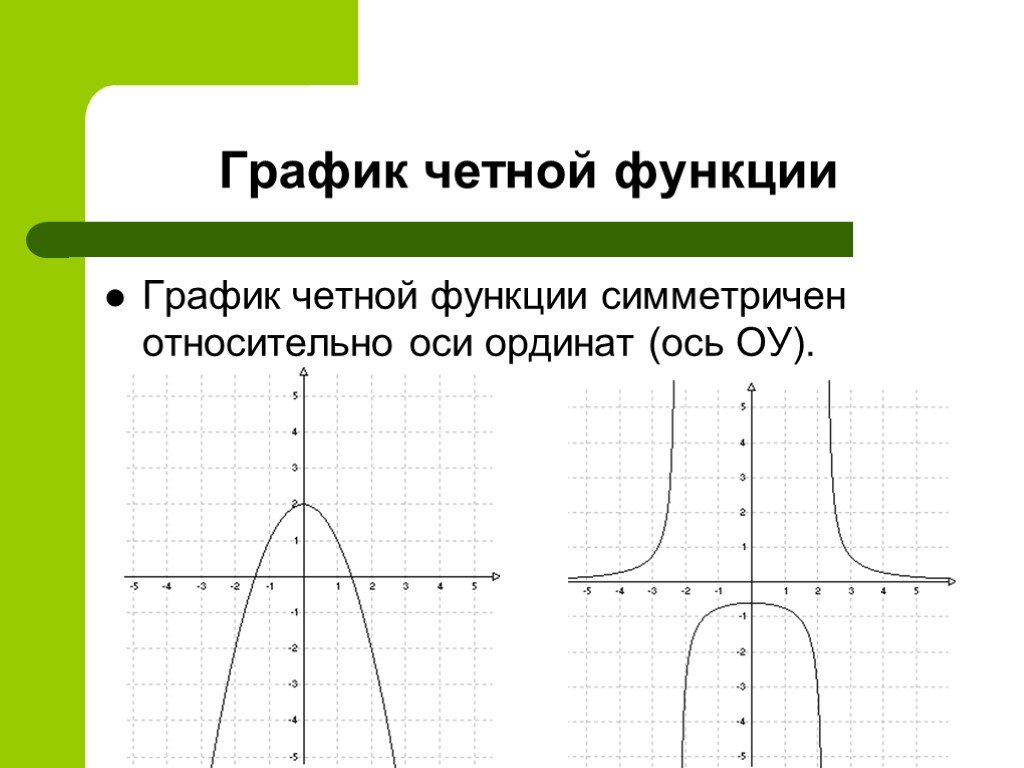
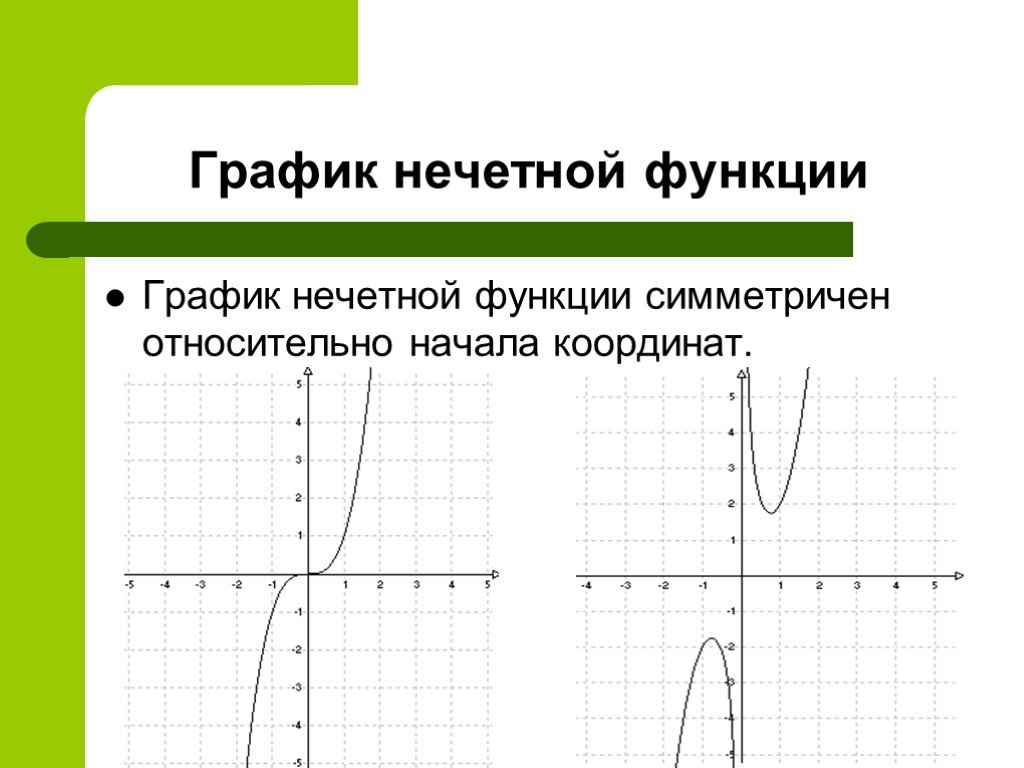
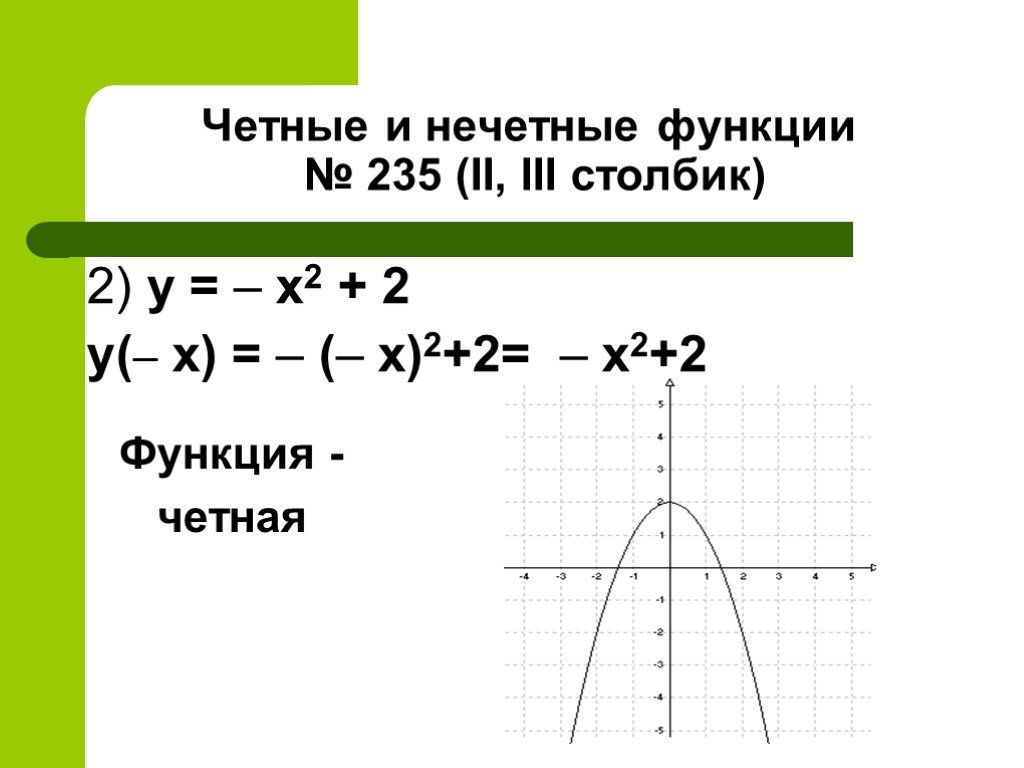
Презентация "Определить, чётная или нечётная функция" по математике – проект, доклад

Скачать презентацию (95.09 Кб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Презентацию на тему "Определить, чётная или нечётная функция" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).

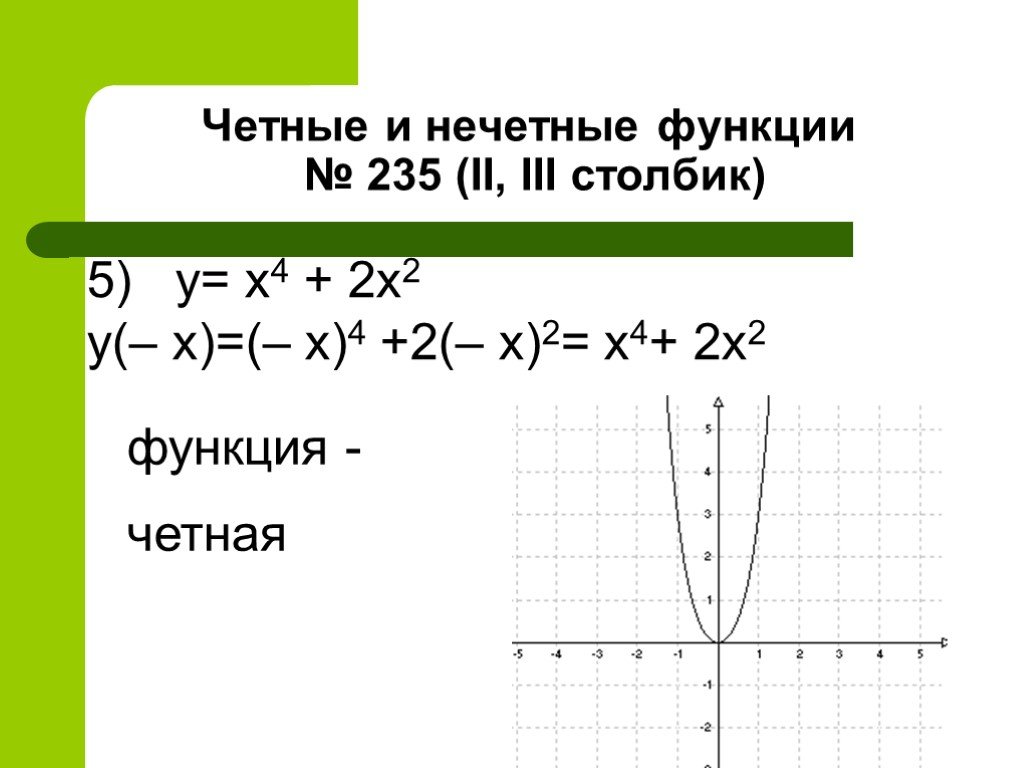
Скачать презентацию (95.09 Кб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Четные и нечетные функции

11 класс 5klass.net

Слайд 2

Симметрия относительно оси Оу и начала координат

Слайд 3

Четные функции

Функция y = f(x) называется четной, если для любого х из области определения функции верно равенство f(-x) = f(x). Чтобы узнать является ли функция четной нужно в функцию f(x) вместо переменной х поставить переменную(–x).

Слайд 4

Например: является ли четной функция f(x) = 3x2 + 2 f(-x) = 3(-x)2 + 2 = 3x2 + 2 = f(x) – функция четная

Слайд 5

f(x) = 2x4 - 3x2 f(x) = x3 - 2x2

f(-x) = 2(-x)4 – 3(-x)2 = 2x4 - 3x2 - четная f(-x) = (-x)3 – 2(-x)2 = – x3 – 2x2 Не является четной

Проверим являются ли данные функции четными

Слайд 6

График четной функции

График четной функции симметричен относительно оси ординат (ось ОУ).

Слайд 7

Нечетные функции

Функция y = f(x) называется нечетной, если для любого х из области определения функции верно равенство f(-x) = - f(x). чтобы узнать является ли функция нечетной нужно в функцию f(x) вместо переменной х поставить переменную (–x) и получить первоначальную функцию с противоположными знаками.

Слайд 8

Например: является ли нечетной функция f(x) = 3x3 + х f(-x) = 3(-x)3 + (-х) = -3x3 - х = -(3x3 + х)= = - f(x) – функция нечетная

Слайд 9

f(x) = 2x4 + 3x f(x) = x3 - 2x

f(-x) = 2(-x)4 + 3(-x) = =2x4 - 3x - не является нечетной f(-x) = (-x)3 – 2(-x) = – x3 + 2x нечетная

Проверим являются ли данные функции нечетными

Слайд 10

График нечетной функции

График нечетной функции симметричен относительно начала координат.

Слайд 11

Четные и нечетные функции № 235 (II, III столбик)

2) y = – x2 + 2 y(– x) = – (– x)2+2= – х2+2

Функция -четная

Слайд 12

5) y= x4 + 2х2 y(– x)=(– x)4 +2(– х)2= х4+ 2х2

функция - четная

Слайд 13

Функции могут быть как четными, нечетными, так и ни четными, ни нечетными.

Пример: y(x) = x2 + 2x y(-x) = (-x)2 + 2(-x) = x2 - 2x

Слайд 14

функция - нечетная

Слайд 15

11) y(x) = x3 + x -1

y(-x) = (-x)3 + (-x)-1 = -x3 - x-1

Функция - нечетная

Список похожих презентаций

Как чётная и нечётная степень влияет на знак числа

Цель: Научиться возводить отрицательное число в степень. Задачи: Выучить правило возведения числа в степень. Научиться применять это правило для решения ...

Показательная функция ее свойства и график

Цель:. Знать понятие степени с иррациональным показателем, определение показательной функции, свойства показательной функции Уметь использовать свойства ...

Показательная функция

Презентация снабжена гиперссылками, при обращении к которым можно сразу перейти на выбранный слайд. Так же используются следующие управляющие кнопки: ...

Морис Эшер - математика или искусство?

Мозаичное искусство Эшера. Регулярные заполнения плоскости. Нерегулярные заполнения плоскости. Литографии с многогранниками. Метаморфозы реальных ...

Логарифмы. Логарифмическая функция

На уроке:. Применение свойств логарифмов. Свойства и график логарифмической функции. Решение примеров из вариантов единого государственного экзамена. ...

Логарифмическая функция

y x y=x. . 0 1 2 3 4 5 6 7 8 9 у = logax 2 1 у = log7x у = log4x у = log2x -3. 0 1 0 4 -2. у х a > 1 0 < a < 1. Логарифмическая функция и её применение. ...

Что такое функция?

Цели урока:. Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины: зависимая переменная и независимая переменная (аргумент ...

Степенная функция

Нам знакомы функции. Прямая Парабола. Кубическая парабола. Гипербола у = х у = х2 у = х3. Все эти функции являются частными случаями степенной функции. ...

Квадратичная функция

План:. Урок 1 Определение квадратичной функции; Функция вида Функция вида Урок 2 Функция вида Функция вида Функция вида Урок 3 Функция вида Урок 4 ...

Дробь как одна или несколько равных долей

Частное от деления натуральных чисел можно записать в виде дроби. Числитель дроби – это делимое, а знаменатель - делитель. пример. знаменатель числитель ...

Золотое сечение или гармоническая пропорция

Учебный проект по математике. Автор проекта: Урбаева Клара Климентьевна, зам. директора ОГОУ НПО ПУ № 59 по общеобразовательным дисциплинам, преподаватель ...

Арифметические действия над числами или зачем туристу математика?

27 сентября – день туриста. 34 х 2 = 90 : 30 = 9 + 45 = 11 х 3 = 80 – 19 = 55 : 5 = И У Р Т С 68 3 54 33 61 11. Что лежит в рюкзаке туриста? спички ...

Алгебра и начала анализа "Логарифмическая функция"

Содержание. Титульный лист Содержание Определение логарифмической функции Свойства логарифмической функции График логарифмической функции Примеры. ...

«Моя математика» - задачи на нахождение целого или части

МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ...

Показательная функция, ее свойства и график

Определение показательной функции. Показательной функцией называется функция у = а , где а – заданное число, а>0, a ≠ 1. х Примеры:. График показательной ...

Квадратичная функция

История параболы. Математики Древней Греции отк- рыли параболу ещё в 260-170 г.г. до нашей эры при изучении коничес- ких сечений. Уже в 17 веке Галилео ...

Соблюдение грамматических норм: незначительность или необходимость?

. Прочитайте отрывок, назовите произведение. И он к устам моим приник, И вырвал грешный мой язык, И празднословный, и лукавый, И жало мудрыя змеи ...

Квадратичная функция

Всякое учение и всякое обучение основано на некотором уже ранее имеющемся знании Аристотель. Устный опрос Сформулировать определение квадратичной ...

Урок Логарифмическая функция

Эпиграф урока:. Потому – то, словно пена, Опадают наши рифмы. И величие степенно Отступает в логарифмы. Борис Слуцкий. Логарифмическая «комедия 2>3». ...

Квадратичная функция

План:. 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Определение:. Квадратичной функцией ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.