Презентация "Сечения многогранников плоскостью" по математике – проект, доклад
Презентацию на тему "Сечения многогранников плоскостью" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 7 слайд(ов).
Слайды презентации
Список похожих презентаций
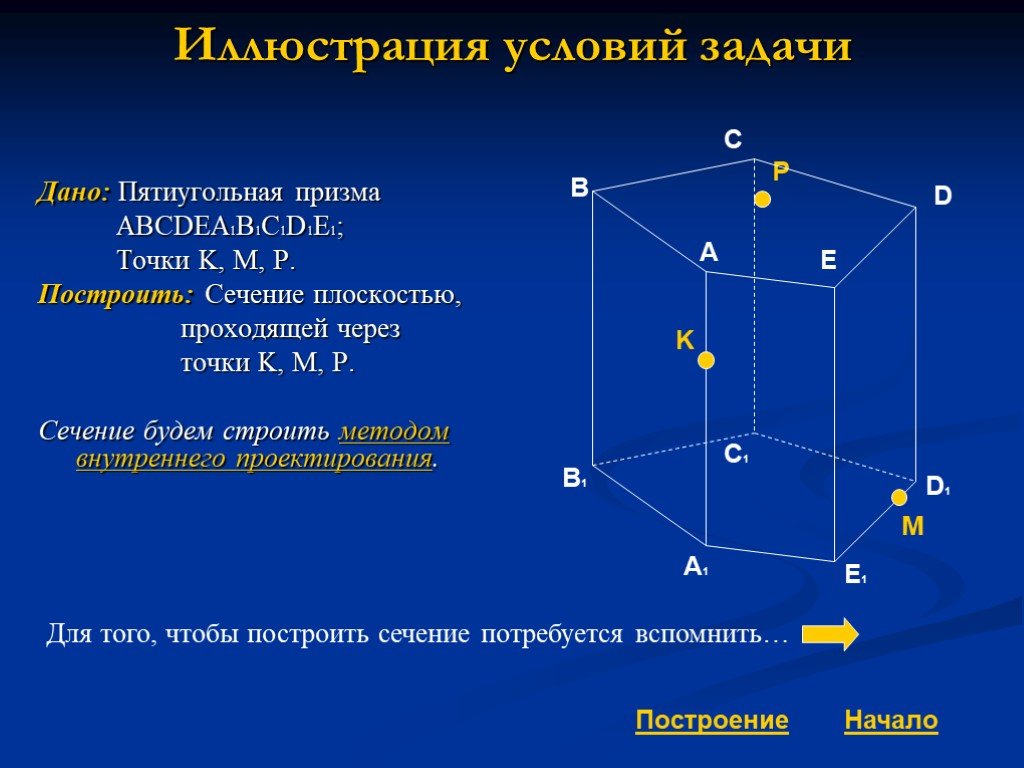
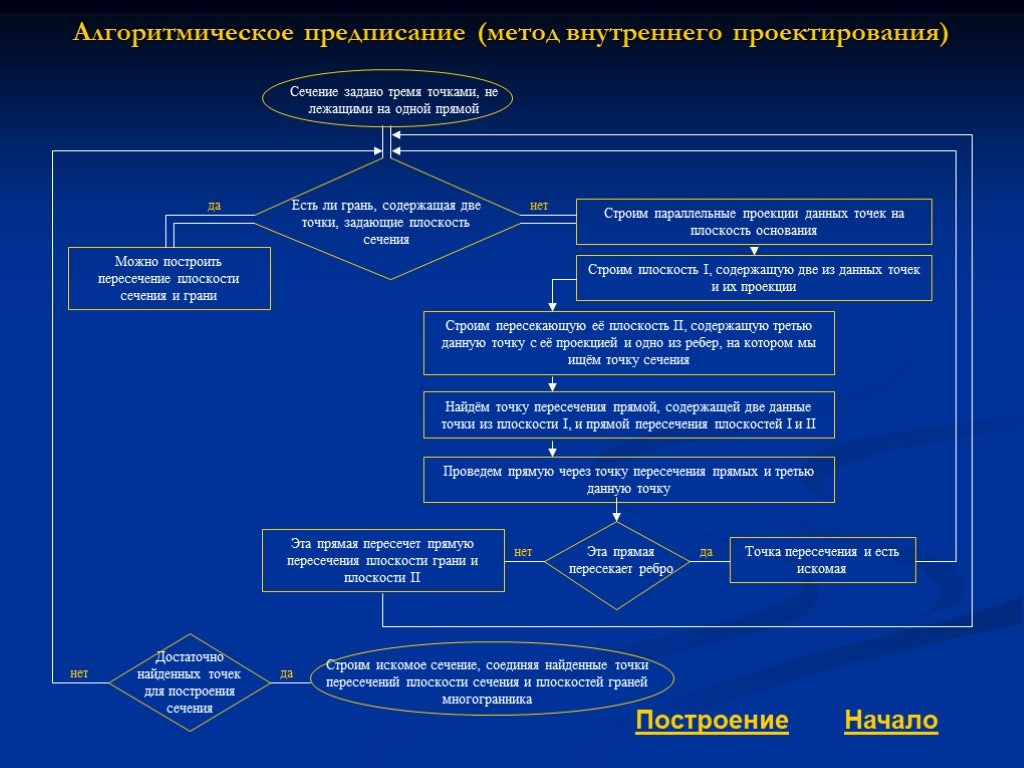
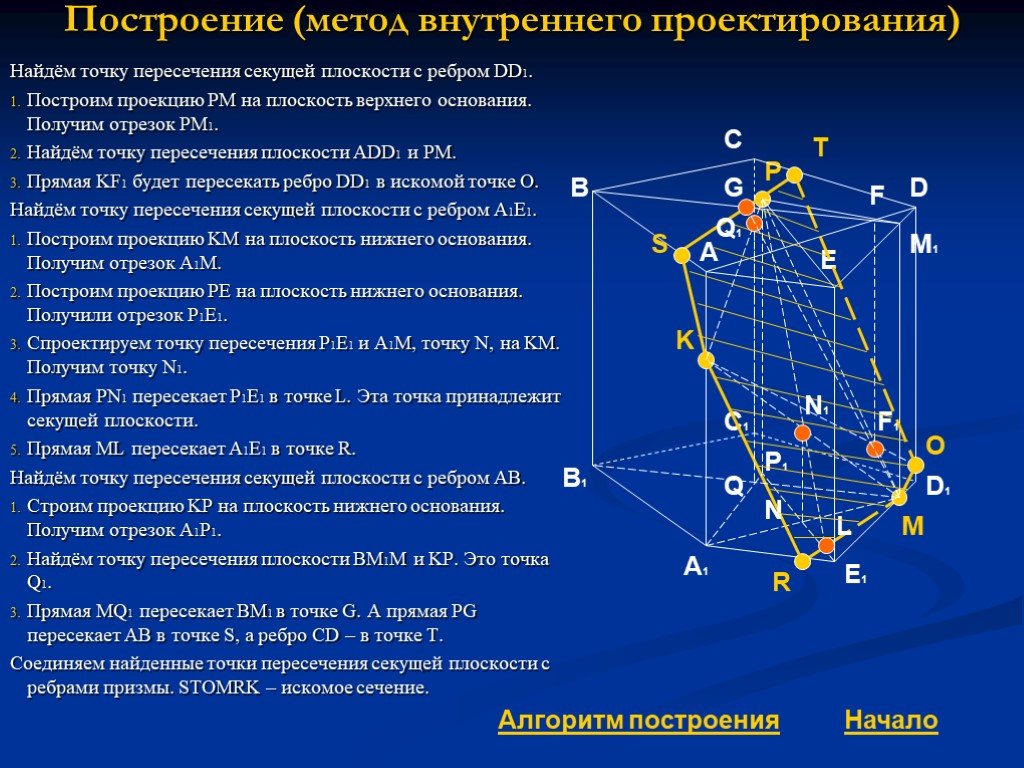
Сечения многогранников
Задача 1 Ответ. . Задача 2. . Задача 3. . Задача 4. . Задача 5. . ...Сечения параллелепипеда
Цель этой презентации « Сечения параллелепипеда» состоит в том, чтобы помочь учащимся понять и усвоить алгоритм построения сечений параллелепипеда. ...Сечения конуса и цилиндра
Математический диктант. 1 1 вариант 2 вариант. Какая фигура получается в сечении конуса плоскостью, проходящей через ось конуса? Какая фигура получается ...Сечения
Сечения. Геометрия 10 -11. формирование и развитие пространственных представлений; выработка навыков решения задач на построение сечений простейших ...Сечение многогранника плоскостью
Содержание Основные понятия. Демонстрация сечений. Метод следов. Метод вспомогательных сечений. Комбинированный метод. Тест Защита проектов. Многогранником ...Применение правильных многогранников
Цель проекта: познакомить учащихся с рядом интересных особенностей правильных многогранников, показать “мир в целом”, преодолев разобщенность научного ...Угол между прямыми. Угол между прямой и плоскостью
Две пересекающиеся прямые в пространстве определяют единственную плоскость, поэтому угол между пересекающимися прямыми в пространстве определяется ...Сечения тетраэдра
C A B D P K M 1 Задача 1 Используем след MP Используем след MK. 2 Задача 2 Используем след PK. Задача 3. Задача 4. Задача 5. Задача 6. 3 Задача 7. ...Модели многогранников
Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны. Существует ...Мир правильных многогранников
Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, ...Классификация и свойства правильных многогранников
Свойства многогранников Многогранники представляют собой простейшие тела в пространстве. Многогранные формы мы видим ежедневно: спичичный коробок, ...Каскады многогранников
Куб и тетраэдр. Тетраэдр можно вписать в куб так, что вершинами тетраэдра будут некоторые вершины куба. Упражнение 1. Найдите ребро тетраэдра, вписанного ...Вклад философов-математиков в развитие теории многогранников
Математика: лабиринты открытий. Стереометрия как наука известна уже очень давно. Изысканиями в этой области занимались многие видные умы древности. ...Виды правильных многогранников
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл. ...Виды многогранников
Геометрия является самым могущественным средством для изощрения наших умственных способностей. Г.Галилей. Многогранником называется тело, ограниченное ...Сечения призмы
Виды призм. Прямая. Правильная. Наклонная. Все призмы делятся на прямые и наклонные. Если боковое ребро призмы перпендикулярно плоскости ее основания, ...Сечения прямоугольного параллелепипеда и тетраэдра
№82. Отметьте внутр.точку М грани АА1В1В. Постр. сеч. прох. ч/з т.М и параллельно а)(АВСD); б)(ВВ1С1С); в)(BDD1). А В С D B1 C1 D1 А1. М1 М. №82 в. ...Моделирование многогранников
Для изготовления модели многогранника из плотной бумаги, картона или другого материала достаточно изготовить его развертку и затем склеить соответствующие ...Угол между прямой и плоскостью
Перпендикулярны ли прямые а и в? Ответ обоснуйте. А В С D F b a. ABCD- прямоугольник, FB┴(ABC). ABCD- параллелограмм, FB┴(ABC). C B O ABCD- ромб, ...Моделирование предмета сложной формы из многогранников
1 3 4 5 6 7. . 2. Задание 1 ( выполняется совместно в команде) Придумать оригинальную форму фонаря, используя различные многогранники, и изобразить ...Конспекты
Удивительный мир многогранников
Урок по геометрии в 10 классе. Разработала учитель математики. МОУ «Гимназия им. Горького А.М.»:. Фабер Г.Н. Тема:. «Удивительный мир многогранников». ...Построение сечений многогранников на основе аксиоматики
Чудаева Елена Владимировна, учитель математики,. МОУ «Инсарская средняя общеобразовательная школа №1»,. г. Инсар, Республика Мордовия. . Автор. ...Построение сечений многогранников
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 1 им. Гриши Акулова. . г.Донецка, Ростовской области. ...Построение сечений многогранников
Государственное бюджетное образовательное учреждение. Лицей №281. «Построение сечений многогранников». Урок геометрии. 10 класс. ...Площади плоских фигур. Пространственные тела. Площади поверхности многогранников
Приложения 1. Разработки уроков с профессиональной направленностью. Урок 1. Тема урока:. . Площади плоских фигур. Пространственные тела. Площади ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:29 мая 2019
Категория:Математика
Содержит:7 слайд(ов)
Поделись с друзьями:
Скачать презентацию