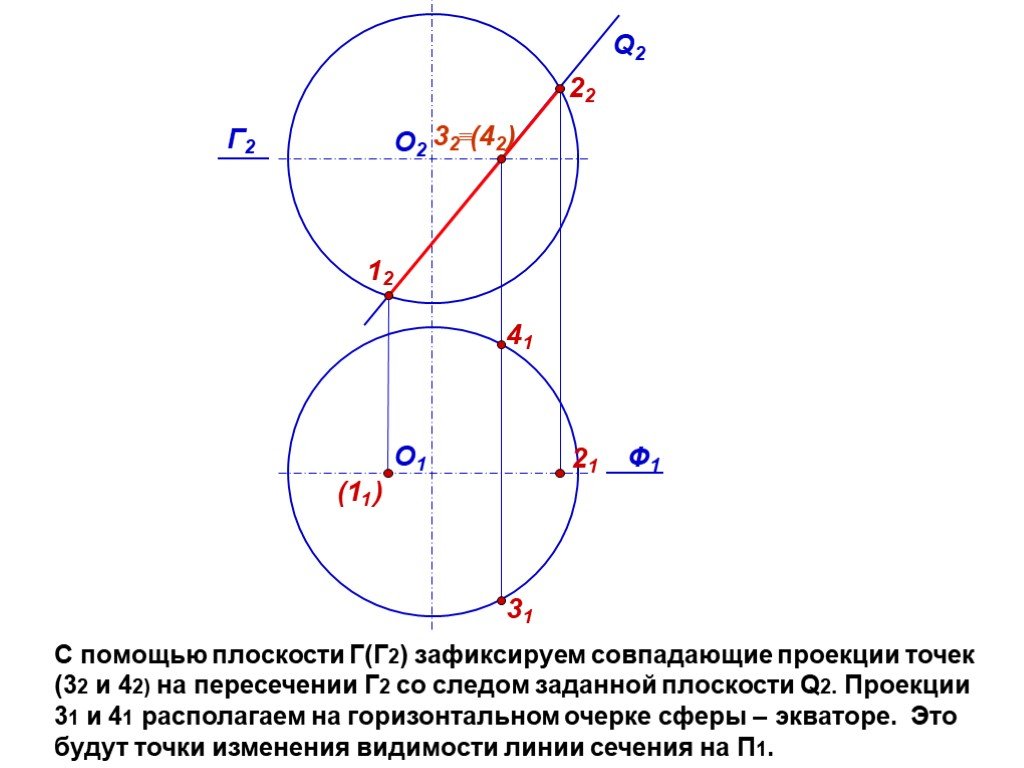
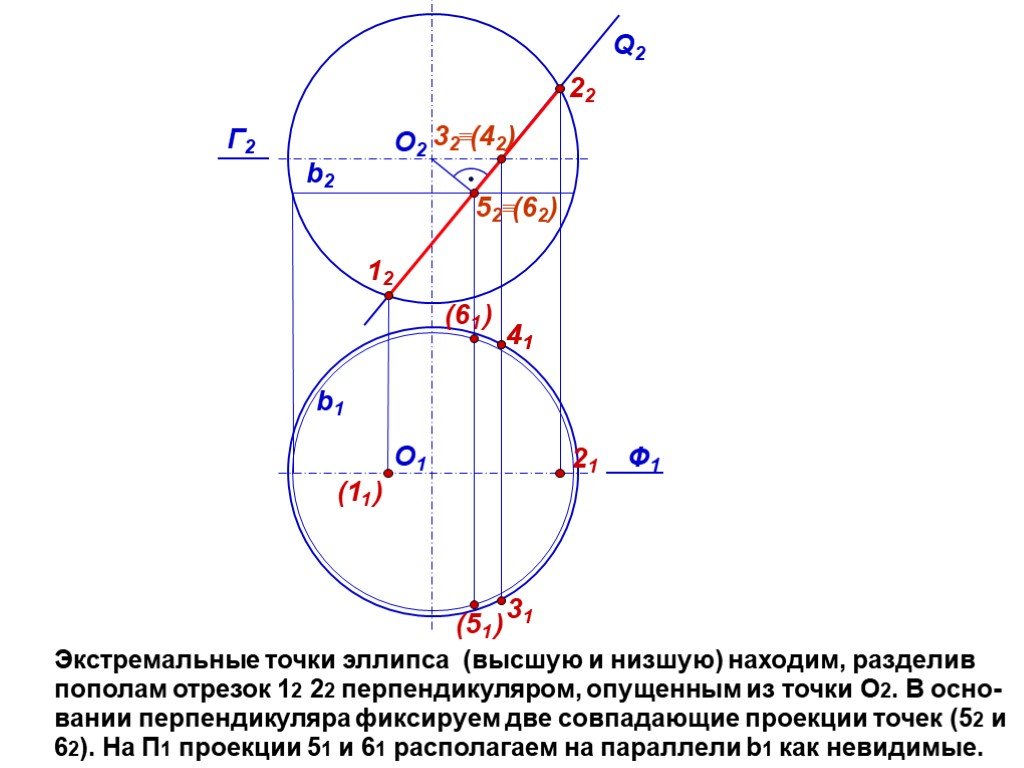
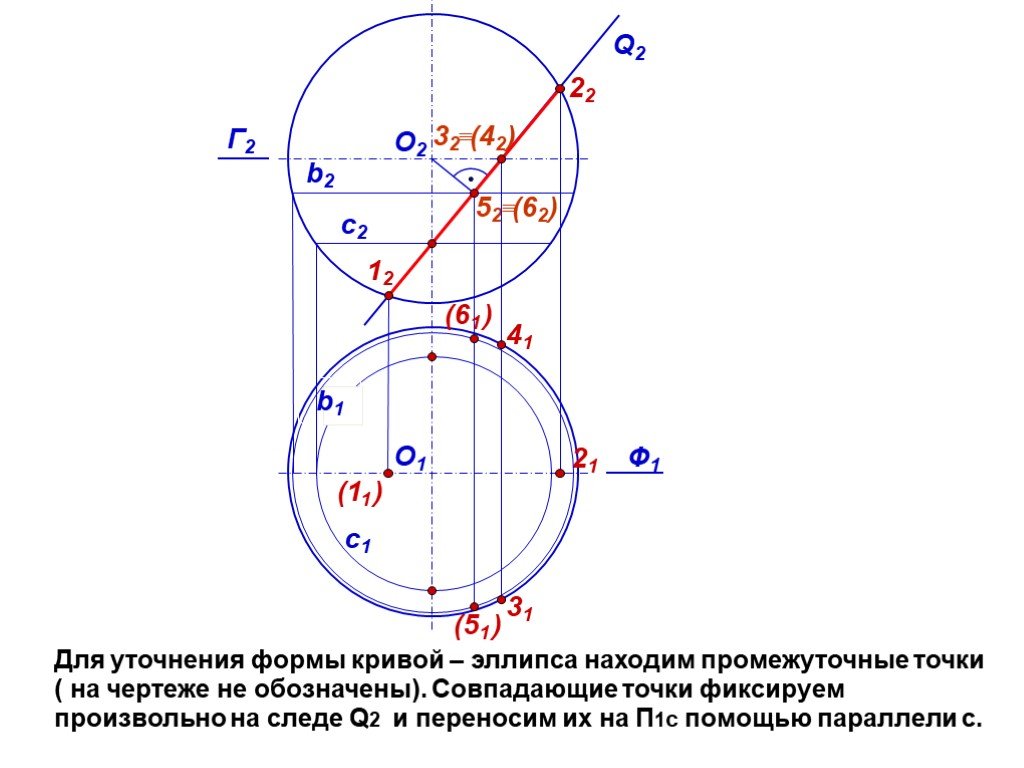
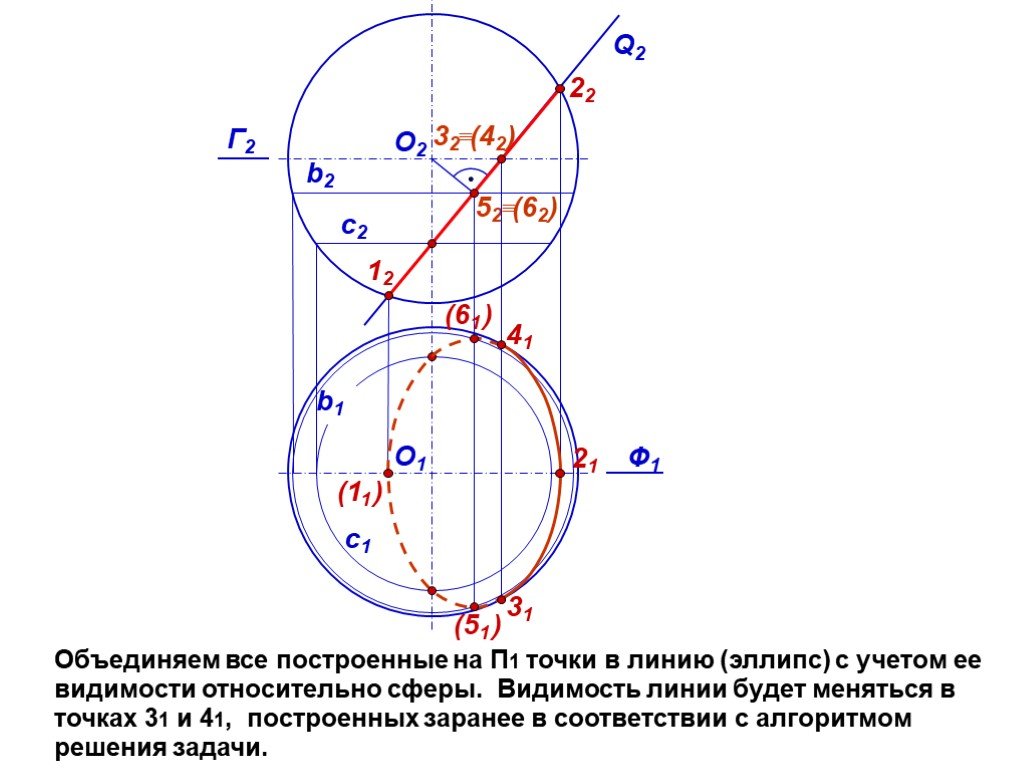
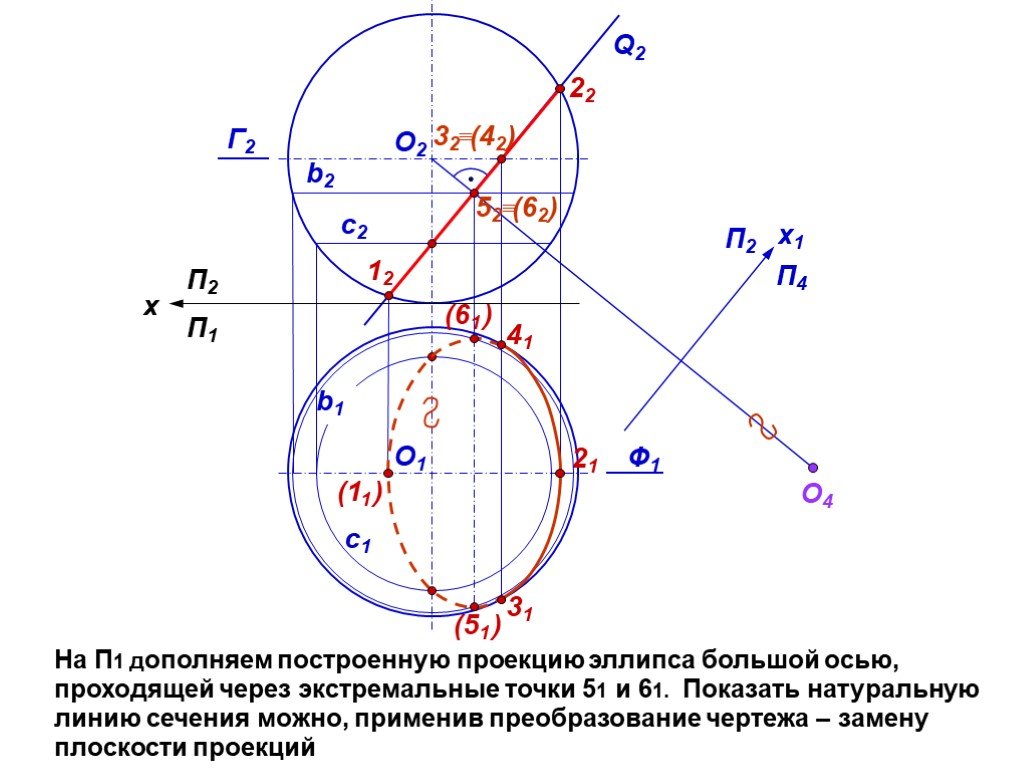
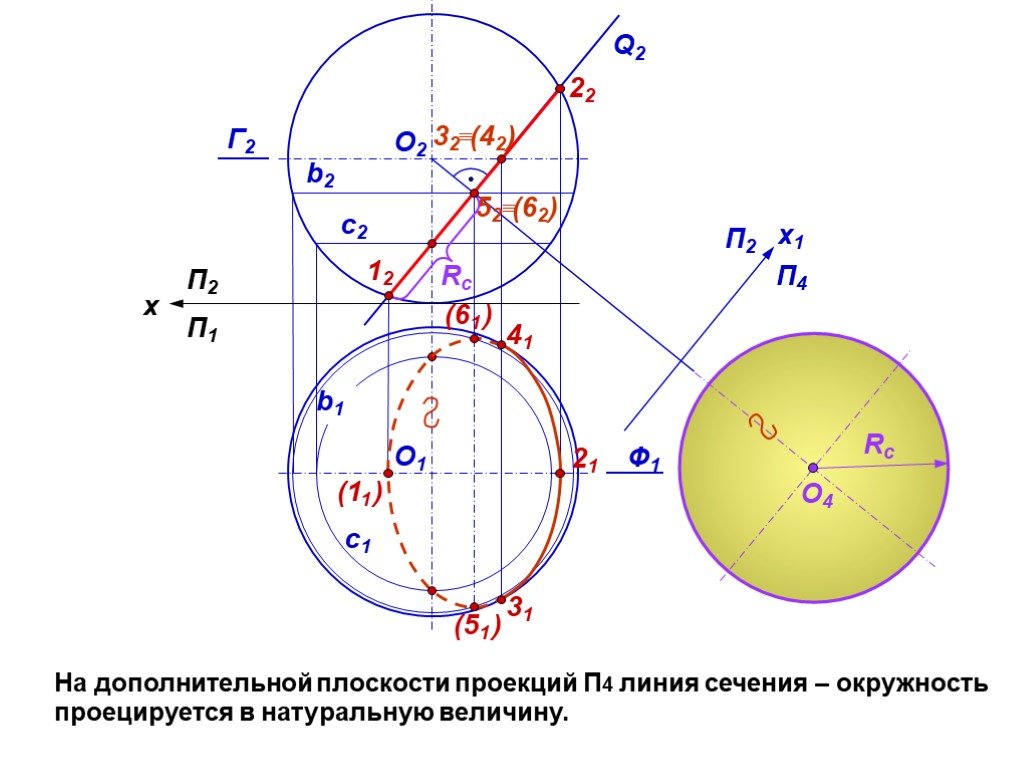
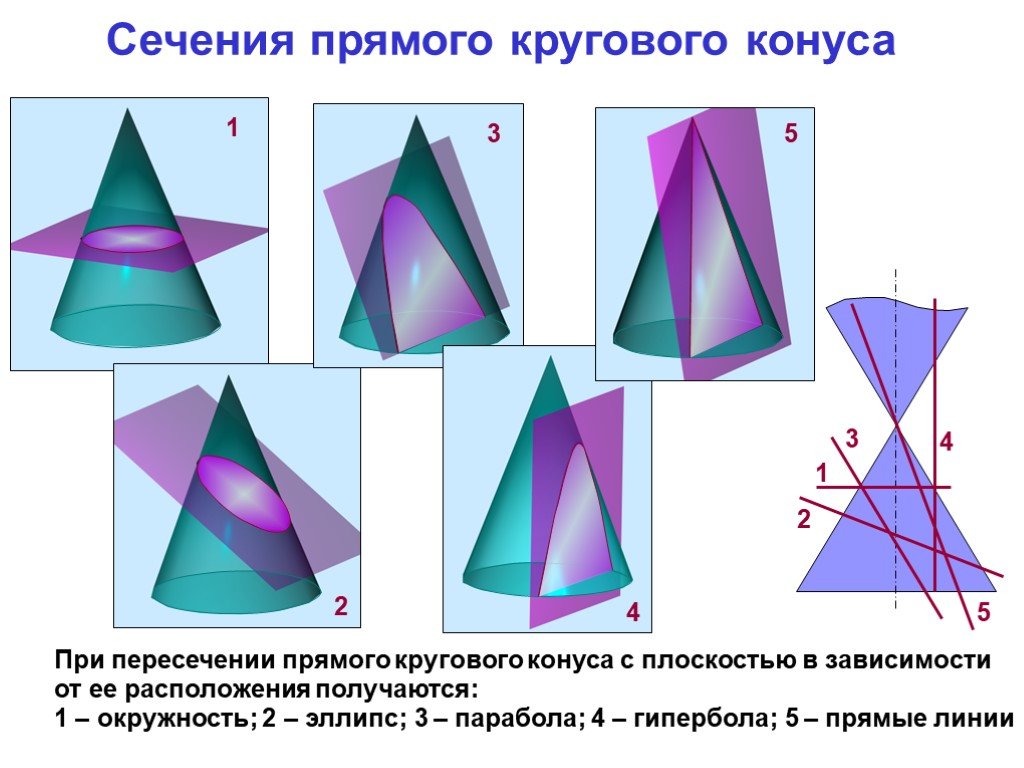
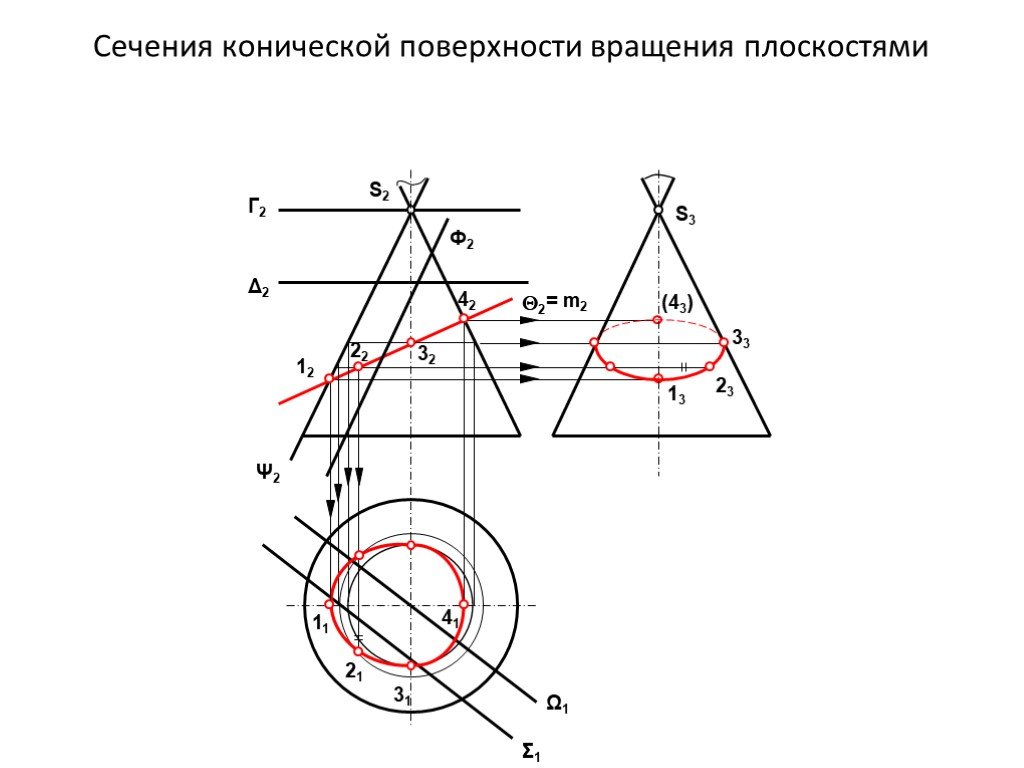
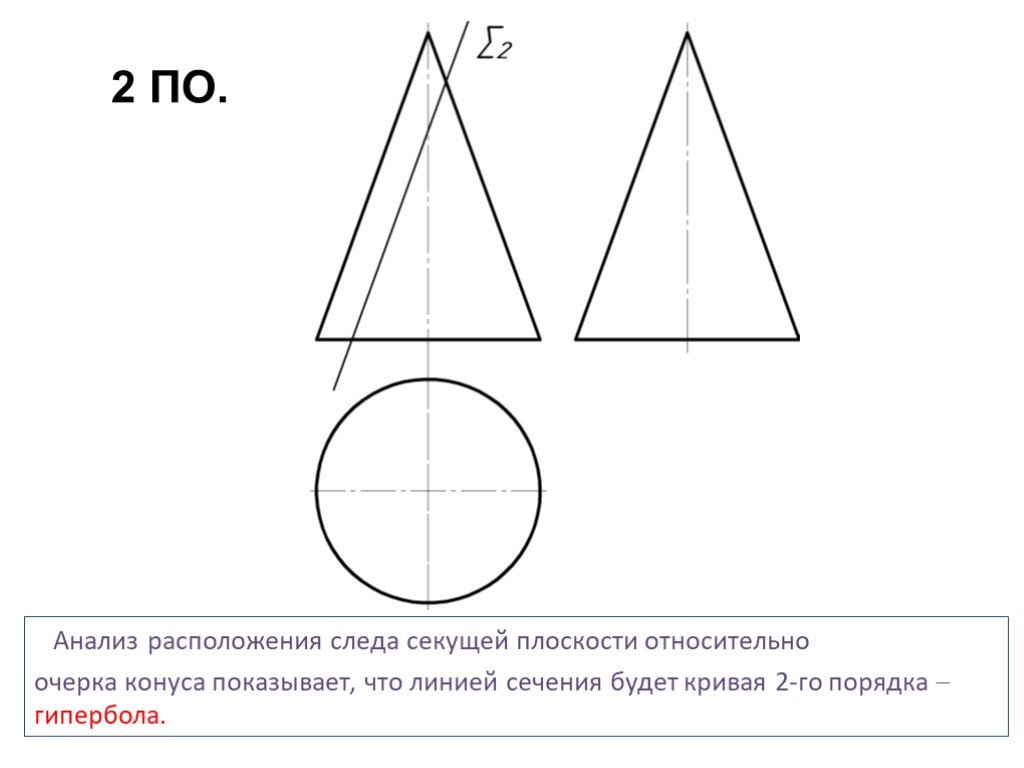
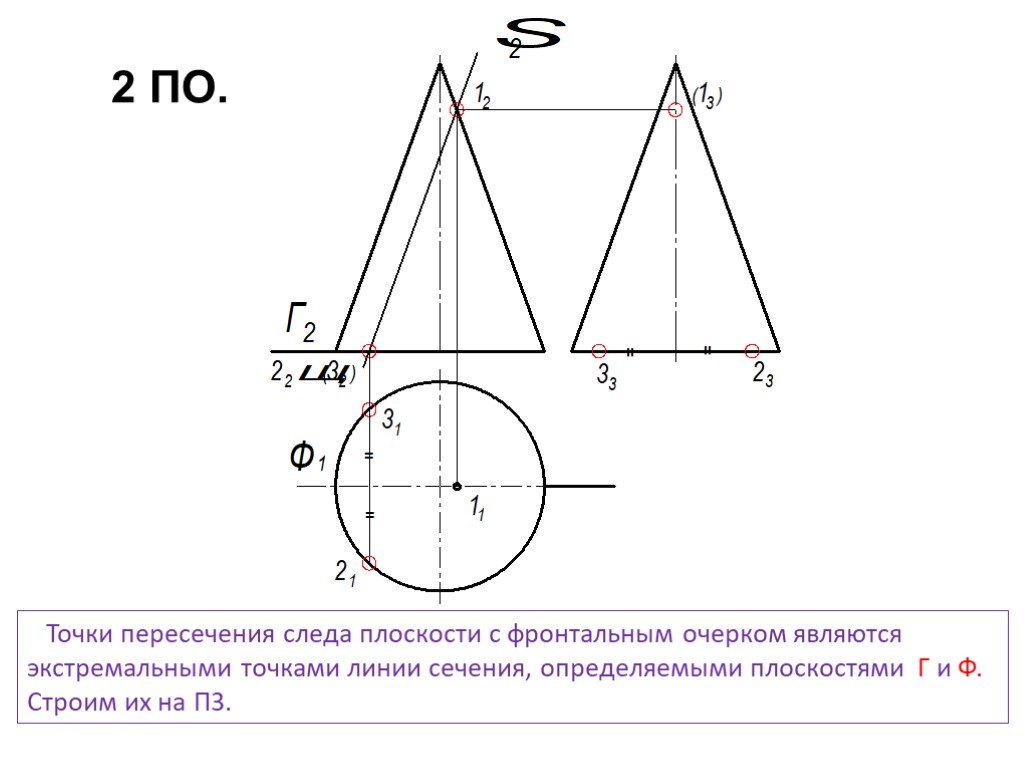
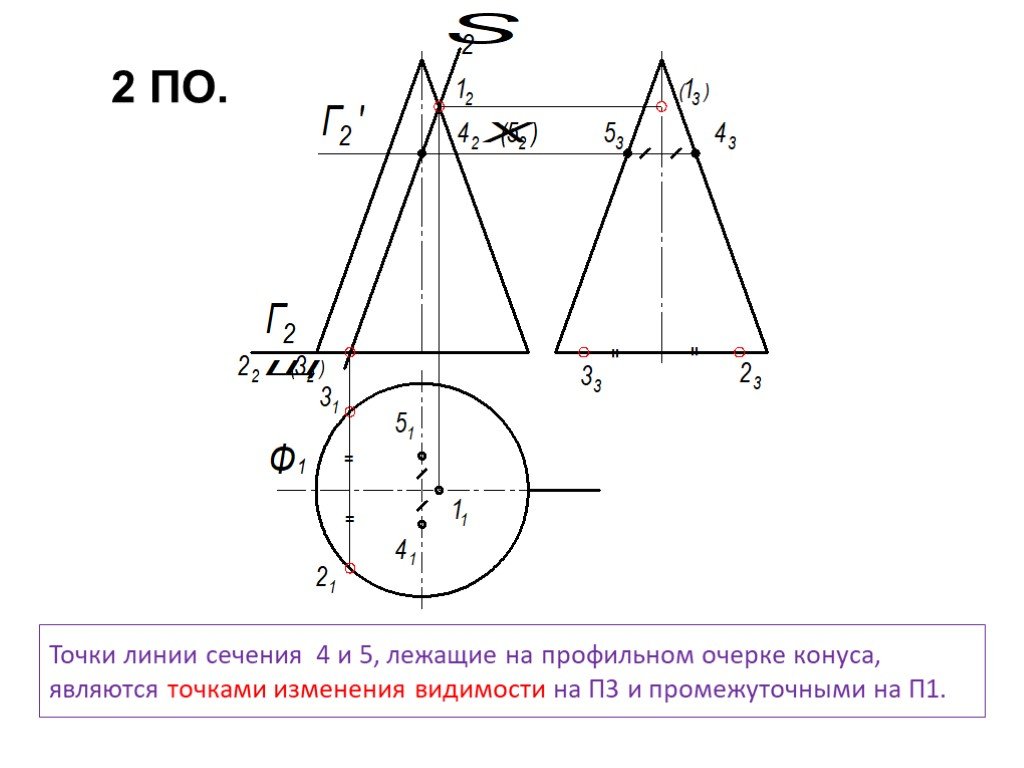
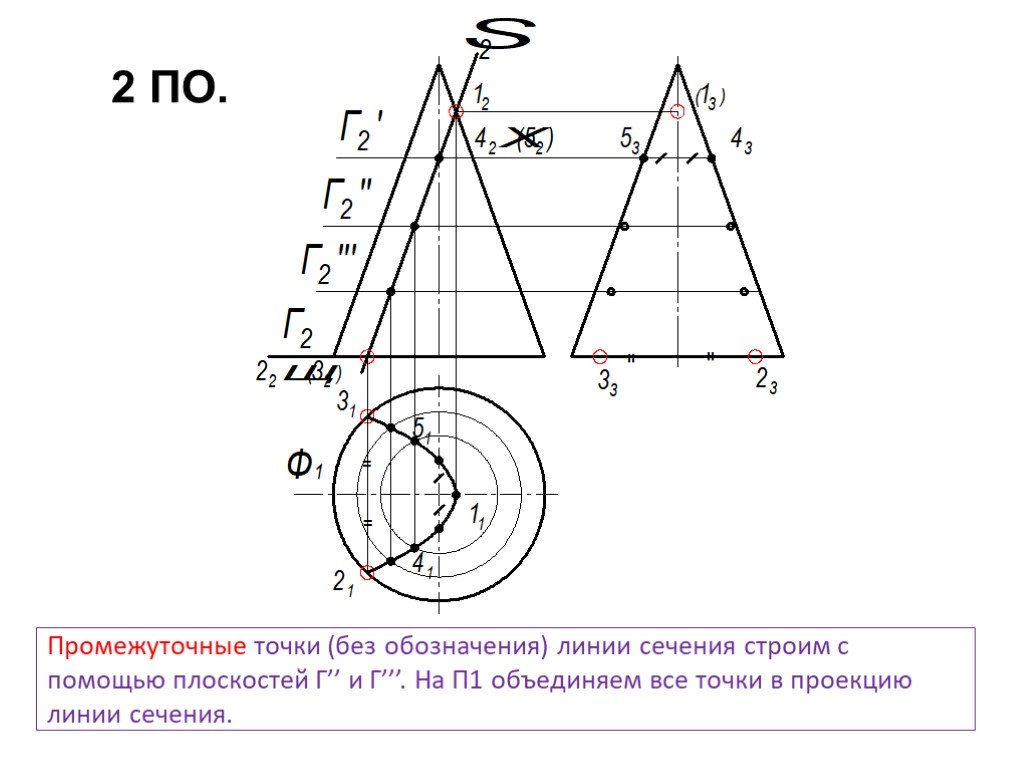
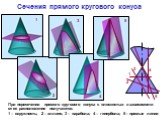
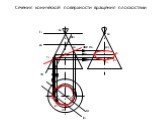
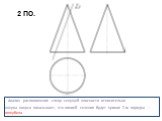
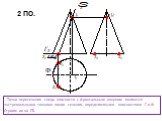
Презентация "сечение поверхности" по математике – проект, доклад
Презентацию на тему "сечение поверхности" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Площадь поверхности конуса
Угадайте зашифрованное тело вращения:. КОНУС – ТЕЛО ВРАЩЕНИЯ. Δ КОВ : КО – ось вращения. К О В. КОНУС. OK=H (высота конуса) OA=OB=OC=R (радиус основания ...Применение формул объёма и площади поверхности прямоугольного параллелепипеда
Цель урока: Научиться на практике применять формулы объёма и площади поверхности прямоугольного параллелепипеда. Устный опрос. Сколько ребер у параллелепипеда? ...Золотое сечение или гармоническая пропорция
Учебный проект по математике. Автор проекта: Урбаева Клара Климентьевна, зам. директора ОГОУ НПО ПУ № 59 по общеобразовательным дисциплинам, преподаватель ...Золотое сечение в математике и в жизни
« В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценность золота, ...Золотое сечение и применение золотого сечения в жизни
Цель работы:. 1.Изучить тему «золотая пропорция». 2.Рассмотреть связанные с нею отношения. 3.Познакомиться с «золотой пропорцией» в природе. Методы ...Золотое сечение
Золотое сечение в архитектуре. то. В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения ...Винтовые поверхности
Винтовая поверхность образуется винтовым перемещением линии (образующей). Поверхность можно задать начальным положением образующей и направляющей ...Золотое сечение
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, ...Золотое сечение
в математике; в анатомии человеческого тела; в скульптуре; в архитектуре; в живописи; в природе; в поэзии и музыке; заключение. Золотое сечение в ...Золотое сечение
Связь между последовательностью Фибоначчи и « Золотым сечением». Последовательность Фибоначчи. Наибольший интерес представляет для нас сочинение "Книга ...Золотое сечение
План проекта: ввести понятие «золотое сечение» геометрическое построение «золотого сечения» построение правильного пятиугольника пентаграмма – символ ...Золотое сечение
ОСНОВАТЕЛИ УЧЕНИЯ О ЗОЛОТОМ СЕЧЕНИИ. Пифагор Ввел понятие о золотом делении. Леонардо да Винчи Ввел термин «золотое сечение». Золотое сечение – это ...Тела и поверхности вращения
Цилиндр Ось цилиндра. Основание цилиндра. Образующие цилиндра. Радиус цилиндра. h 2Пr S = 2Пrh бок V = S h осн. О А Р Конус Ось конуса Основание конуса ...Золотое сечение
«...Геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе - с ...Цилиндры и цилиндрические поверхности
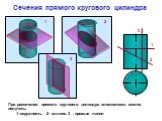
План урока. Цилиндрическая поверхность Сечение круговой цилиндрической поверхности Уравнение круговой цилиндрической поверхности Понятие цилиндра ...Золотое сечение
Сегодня мы познакомимся с необычной пропорцией, называемой золотым сечением и даже “божественной пропорцией”. Вы узнаете какую роль играет эта пропорция ...Золотое сечение в математике
Принципы «золотого сечения» используются в математике, физике, биологии, астрономии и др. науках, в архитектуре и др. искусствах. Они лежат в основе ...Золотое сечение - божественная мера красоты
Предмет исследования: элементы, связанные друг с другом золотой пропорцией, большинству людей кажутся красивыми, такая пропорция создает зрительное ...Золотое сечение вокруг нас
Актуальность. 1. Увлекательная история «Божественной пропорции» 2.Всеобщий характер исследуемого материала 3.Познание законов гармонии и красоты. ...Конспекты
Пропорция. Золотое сечение
Урок по теме «Пропорция. Золотое сечение». Муниципальное общеобразовательное учреждение. . средняя школа № 7 города Лабинска Краснодарского ...Площадь поверхности прямоугольного параллелепипеда
Тема урока. . Площадь поверхности прямоугольного параллелепипеда. . . Базовый учебник. . Математика, 5 класс, Виленкин. . . . Цель ...Площадь боковой поверхности цилиндра и конуса
Конспект урока по математике. Данные о преподавателе:. Кочерягина Галина Владимировна,. I. квалификационная категория,. . государственное ...Площадь боковой поверхности цилиндра
Площадь боковой поверхности цилиндра. . . . . равна . , а диаметр основания — 8. Найдите высоту цилиндра. . Длина окружности основания ...Площади плоских фигур. Пространственные тела. Площади поверхности многогранников
Приложения 1. Разработки уроков с профессиональной направленностью. Урок 1. Тема урока:. . Площади плоских фигур. Пространственные тела. Площади ...Объем и площадь поверхности конических тел
Урок 4. Тема урока: «Объем и площадь поверхности конических тел». Тип учебного занятия:. изучение и первичное закрепление новых знаний и способов ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:7 августа 2019
Категория:Математика
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию