Презентация "Показательная функция" по математике – проект, доклад
Презентацию на тему "Показательная функция" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Показательная функция, ее свойства и график
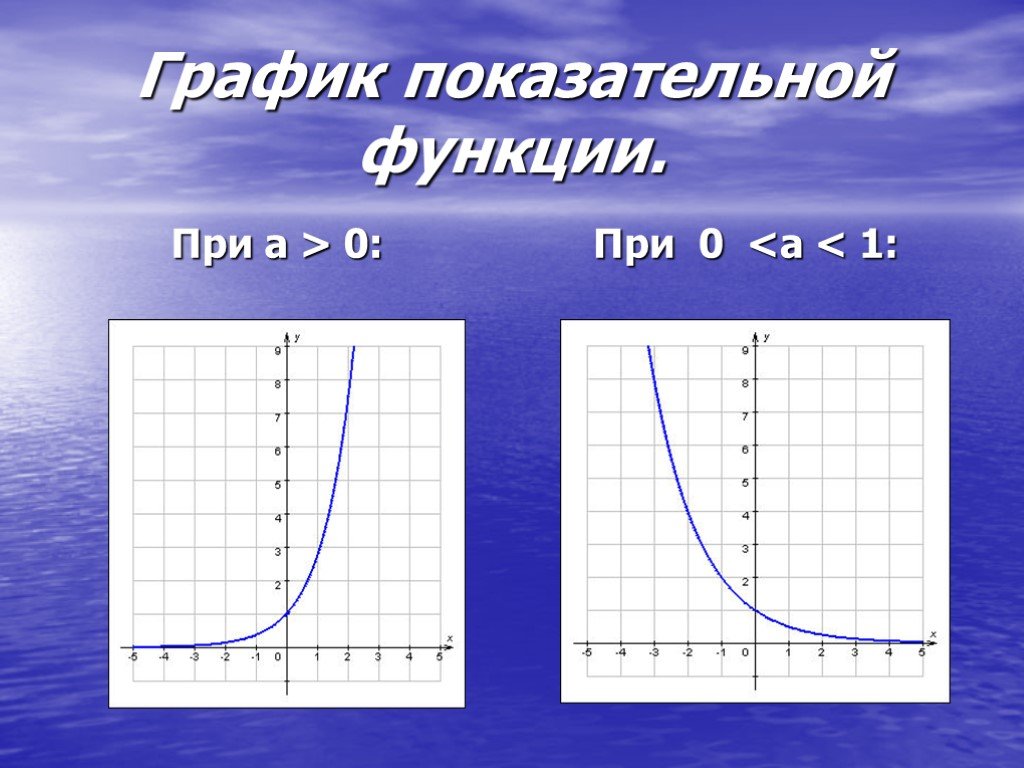
Свойства показательной функции:. Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией. Область определения показательной ...Показательная функция: свойства, график
Найдите лишнюю функцию.1) У=х2 2) у=2х2 3) 4) у=2х 5) 6) у=2х4 7) 8). Показательная функция.
y = а x ; где а>0, a ≠ 1.
Выполнила учитель математики ...
Показательная функция, её свойства и график
. Рост древесины происходит по закону, где: A- изменение количества древесины во времени; A0- начальное количество древесины; t-время, к, а- некоторые ...Показательная функция урок
Цели урока: Образовательная: ввести понятие показательной функции, рассмотреть ее свойства и построить график. Применить изученные свойства показательной ...Показательная функция, ее свойства и график
Определение показательной функции. Показательной функцией называется функция у = а , где а – заданное число, а>0, a ≠ 1. х Примеры:. График показательной ...Показательная функция и ее свойства
"Дорогу осилит идущий, а математику - мыслящий". Вопросы: Независимая переменная (х) Наглядный способ задания функции (графический) График четной ...Показательная функция и её свойства
Показательная функция. В практике часто используются функции y=2x, y=10x, y=(0,1)x и т. д., т. е. функция вида y=ax где а - заданное число, x -переменная. ...Показательная функция
Определение. Функцию вида называют показательной функцией. Основные свойства. График функции Кривая называется экспонентой а>1. 0. Геометрическая ...Показательная функция ее свойства и график
Цель:. Знать понятие степени с иррациональным показателем, определение показательной функции, свойства показательной функции Уметь использовать свойства ...Показательная функция
Цель:. Рассмотрение основных свойств показательной функции. Построение графика. Решение показательных уравнений. Решение показательных неравенств. ...Показательная функция
"Дорогу осилит идущий, а математику - мыслящий". Вопросы: Независимая переменная (х) Наглядный способ задания функции (графический) График четной ...Показательная функция. Показательные уравнения
Автор: Кашина Галина Васильевна, преподаватель математики Тип урока: урок обобщения, систематизации знаний. Цели урока: Образовательные: Обобщить ...Урок итогового повторения. Показательная функция. Решение показательных уравнений и неравенств.
Повторение изученного материала. Дайте определение показательной функции. Перечислите основные свойства показательной функции. Изобразите схематически ...Показательная функция
Презентация снабжена гиперссылками, при обращении к которым можно сразу перейти на выбранный слайд. Так же используются следующие управляющие кнопки: ...Логарифмы. Логарифмическая функция
На уроке:. Применение свойств логарифмов. Свойства и график логарифмической функции. Решение примеров из вариантов единого государственного экзамена. ...Логарифмическая функция
y x y=x. . 0 1 2 3 4 5 6 7 8 9 у = logax 2 1 у = log7x у = log4x у = log2x -3. 0 1 0 4 -2. у х a > 1 0 < a < 1. Логарифмическая функция и её применение. ...Логарифмическая функция в уравнениях
«Расскажи мне, и я забуду, покажи мне, и я запомню, дай мне сделать самому, и я пойму» О. Хайям. Урок построен по этапам:. 1-й «Потяни за ниточку» ...Линейная функция
Цели:. Напомнить понятие координатной плоскости. Рассмотреть изображение точки на координатной плоскости. Дать понятие об уравнении с двумя переменными, ...Логарифмическая функция
Содержание. 1. Понятие логарифма. 2. Графики логарифмических функций. 3. Свойства логарифмов. 4. Решение логарифмических уравнений. 5. Решение логарифмический ...Конспекты
Показательная функция, ее свойства и график
Конспект урока. Разработчик:. Фарахиева Наталья Анатольевна – преподаватель математики первой квалификационной категории АУ СПО «Чебоксарский техникум ...Показательная функция, её свойства и график
Государственное областное бюджетное. профессиональное образовательное учреждение. «ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ». Методическая разработка. ...Показательная функция, ее свойства и график
Предмет:. алгебра, класс: 10 класс. В Классе 2 ученика. . Тема урока:. «Показательная функция, ее свойства и график». Тип урока:. Изучение нового ...Показательная функция, её график и её свойства
Муниципальное бюджетное образовательное учреждение. . дополнительного образования детей. . «Федоровский дом детского творчества». ...Показательная функция, её график и её свойства
Муниципальное бюджетное образовательное учреждение. . дополнительного образования детей. . «Федоровский дом детского творчества». Сургутского ...Показательная функция
Спицына Татьяна Дмитриевна. Учитель математики. МБОУ «Таксимовская СОШ №1 имени А.А.Мезенцева». Таксимо, Республика Бурятия. Урок по алгебре ...Показательная функция
Автор: учитель математики МОУ «Средняя общеобразовательная школа №41». . г.о. Саранск Тарабина Галина Михайловна. Урок – семинар по теме: « Показательная ...Показательная функция
5. . Тема урока: «Показательная функция». Класс: 11. Ельцова Наталия Ивановна,. . учитель математики. . МОУ «Александровская СОШ». ...Показательная функция
Урок по теме: «Показательная функция». (10 класс). Цель урока:. . обеспечить усвоение каждым учащимся знаний о показательной функции, её свойствах, ...Показательная функция
Автор: Морина Светлана Алексеевна. Учитель математики МБОУ СОШ №5 города-курорта Железноводска. Урок по теме «Показательная функция». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 июля 2019
Категория:Математика
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию