Презентация "Площадь прямоугольного треугольника" по математике – проект, доклад
Презентацию на тему "Площадь прямоугольного треугольника" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
Площадь прямоугольного треугольника
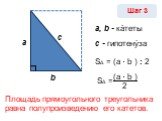
Есть желание, путь найдется! . ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА. S = S : 2 S = a x b: 2. 6 см 5 см 4 см. гипотенуза катет. b a. Треугольник. Измерить ...Площадь прямоугольного треугольника
Геометрия – правительница всех мыслительных изысканий. М.В. Ломоносов. Назови лишнюю геометрическую фигуру. По схеме составь задачу и реши ее. a=21 ...Площадь прямоугольного треугольника
1 3 4. Единицы измерения площадей. За единицы измерения площадей приняты площади квадратов со сторонами, равными единичным отрезкам 1 мм, 1 см, 1 ...Тема: «Площадь прямоугольного треугольника»
Цели:. познакомить с алгоритмом нахождения площади прямоугольного треугольника; учить находить площадь прямоугольного треугольника по его катетам; ...Площадь прямоугольного треугольника
Виды треугольников. По размерам сторон. По размерам углов разносторонние равнобедренные равносторонние прямоугольные остроугольные тупоугольные. острый ...Площадь параллелограмма, треугольника, трапеции
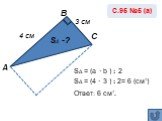
Вычисление площадей фигур на клетчатой бумаге. 1 3 4 5 6 7 8 9 10 11. Найдите площадь фигуры:. Ответ: 6 см² №1. №2. 12 см² №3. №4. 28 см² №5. №6 ...Теорема Пифагора для прямоугольного треугольника
Пифагор Самосский — древнегреческий философ, математик и мистик, создатель религиозно -философской школы пифагор - ейцев. Историю жизни Пифагора трудно ...Соотношения между сторонами и углами прямоугольного треугольника
Найти: 1) sinA, 2) cоsA, 3) tg A Ответ: sin A= Ответ: соsA= tg A=. Дано: АВСD – трапеция, АВ = 16 см, ВАD = 30, СDА = 45. Найти: ВК и ...Соотношения между сторонами и углами прямоугольного треугольника"
Цели:. формирование умений и навыков в применении соотношений между сторонами и углами прямоугольного треугольника; формирование умений работать с ...Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Вопросы для повторения:. Пропорциональные отрезки: 1. Высота, проведённая из вершины прямого угла на гипотенузу в прямоугольном треугольнике, делит ...Синус, косинус, тангенс острого угла прямоугольного треугольника
Синус, косинус, тангенс острого угла прямоугольного треугольника. Расположение углов и сторон. А С В b c a. АС – противолежащий катет. ВС – прилежащий ...Решение задач на нахождение площади прямоугольного треугольника
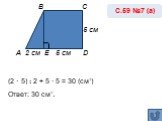
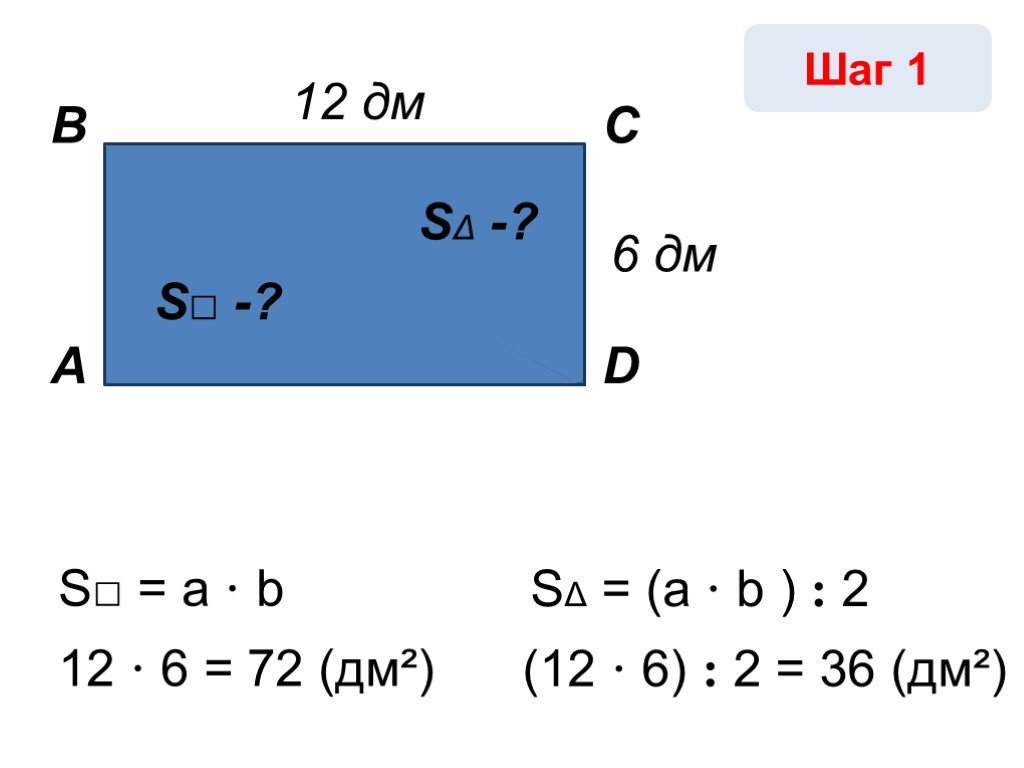
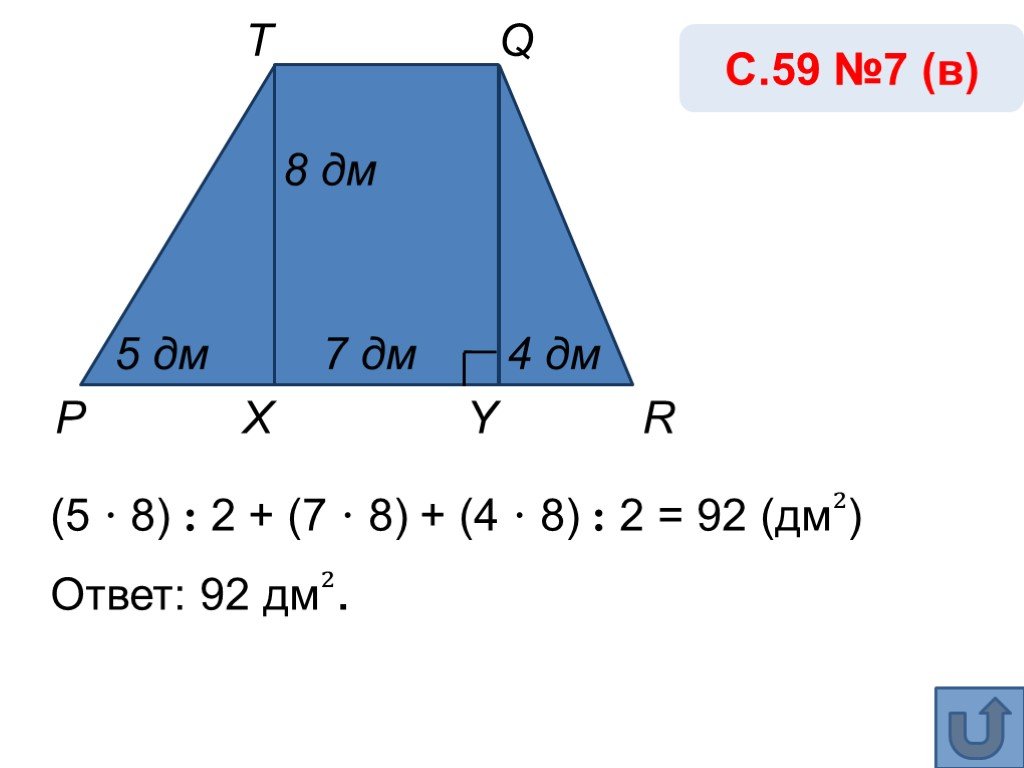
Решить задачи (устно). Р - ? S - ? 12 дм S - ? P = 56 см. P - ? 7 м S = 77 м2 3 см 4 см 6см 13 см = 38 дм R - ? Решить задачу А B C D 2 см = 16 см ...Соотношения между сторонами и углами прямоугольного треугольника
ОТНОШЕНИЕ ПРОТИВОЛЕЖАЩЕГО КАТЕТА К ГИПОТЕНУЗЕ. ТО, ЧТО ВЫРАЖАЕТ ТЕОРЕМА: «ЕСЛИ ДВА УГЛА ОДНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ДВУМ УГЛАМ ДРУГОГО ...Площадь треугольника
АС- основание ВН- высота; ВС- основание АН1- высота. Теорема. Площадь треугольника равна половине произведения его основания на высоту. Док-во: АВС= ...Решение прямоугольного треугольника
1)∟А + ∟В = 900 , sinA = cosB 2)с2 = а2 + в2 3)а = с cosβ в = с sinβ tgB = в/а. О – середина АВ ( О – центр описанной окружности) R- радиус описанной ...Площадь треугольника. Полезные теоремы, следствия и задачи
Вспомните ответы на вопросы. 1) Сформулируй понятие площади геометрической фигуры. 2) Сформулируй основные свойства площадей геометрических фигур. ...Площадь треугольника
Площадь треугольника. Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию. Основания и высоты треугольника. ...Площадь треугольника
Устная работа. А В С D 6 см 10 см К. ABCD – параллелограмм. Найти площадь параллелограмма. 5 см 8 см. Теорема о площади треугольника. Дано: ABD – ...Площадь треугольника
Человек, вооруженный знаниями способен решить любые задачи. Свойства площадей. Равные многоугольники имеют равные площади. F = H S1 = S2 S1 S2. ...Соотношения между сторонами угла прямоугольного треугольника
─ Ввести понятие синуса, косинуса, тангенса, котангенса, секанса, косеканса острого угла прямоугольного треугольника. ─Научиться решать прямоугольные ...Конспекты
Площадь прямоугольного треугольника
Муниципальное бюджетное общеобразовательное учреждение. гимназия №19 имени Поповичевой Н.З. г. Липецка. Конспект урока по ...Площадь прямоугольного треугольника
Муниципальное общеобразовательное учреждение гимназия № 10. Урок по математике УМК “Школа 2100” 4 класс. «Площадь прямоугольного треугольника». ...Площадь прямоугольного треугольника
Конспект урока по математике. Тема: «Площадь прямоугольного треугольника». Тип урока:. изучение нового материала. Цель урока:. создать условия ...Площадь прямоугольного треугольника
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №1». Занятие. . по. . наглядной. . геометрии. . в. 3. классе. ...Площадь прямоугольного треугольника
Урок математики. . по теме. "Площадь прямоугольного треугольника". Основные цели:. 1) Сформировать представление о прямоугольном треугольнике, ...Формула площади прямоугольного треугольника
Тема: «Формула площади прямоугольного треугольника». 4 класс, «Школа 2100…». Форма урока:. урок с мультимедийным сопровождением. Цели. : - выведение ...Высота прямоугольного треугольника
ДОБРОВА НАТАЛИЯ МАРАТОВНАучитель математики. ГБОУ СОШ № 44. Санкт-Петербург. «ВЫСОТА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА». (среднее арифметическое ...Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника (8-й класс). Цели:. Совершенствовать. навыки решения прямоугольных треугольников. ...Соотношения между сторонами и углами прямоугольного треугольника
МОУ «Лицей №31». Методическая разработка урока. по геометрии в VIII. классе. по проблеме: «Личностно-ориентированный подход ...Синус, косинус, тангенс. Площадь треугольника
Автор: Чичерова Татьяна Ивановна. Место работы: МОУ «Образцовская СОШ». Должность: учитель математики. . . Урок геометрии в 9 классе. Тема: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:20 июня 2019
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию


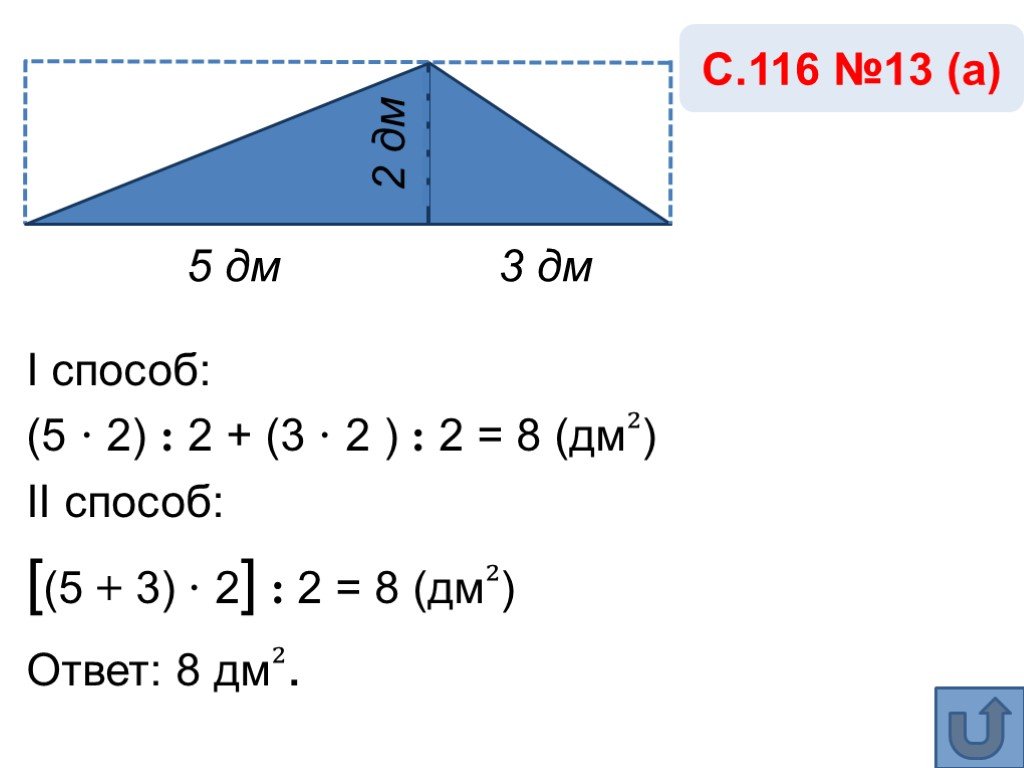



![5 дм 3 дм 2 дм. I способ: (5 · 2) : 2 + (3 · 2 ) : 2 = 8 (дм₂) II способ: [(5 + 3) · 2] : 2 = 8 (дм₂) Ответ: 8 дм₂. 5 дм 3 дм 2 дм. I способ: (5 · 2) : 2 + (3 · 2 ) : 2 = 8 (дм₂) II способ: [(5 + 3) · 2] : 2 = 8 (дм₂) Ответ: 8 дм₂.](https://prezentacii.org/upload/cloud/19/06/155159/images/thumbs/screen10.jpg)

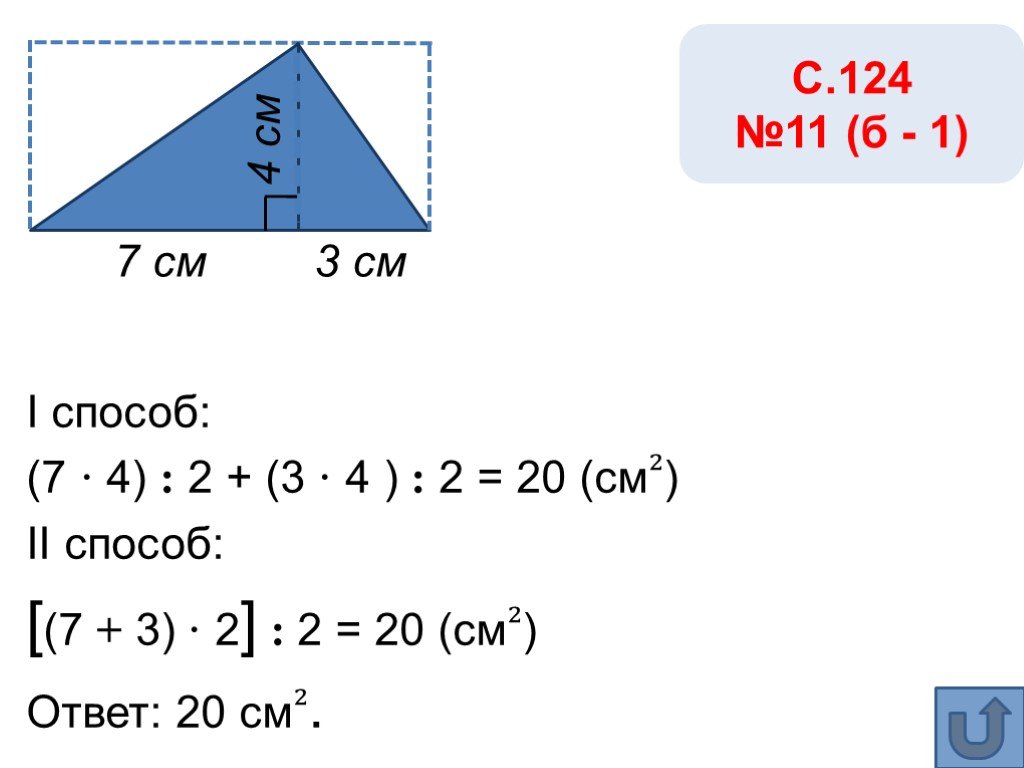
![I способ: (7 · 4) : 2 + (3 · 4 ) : 2 = 20 (см₂) II способ: [(7 + 3) · 2] : 2 = 20 (см₂) Ответ: 20 см₂. 7 см С.124 №11 (б - 1) I способ: (7 · 4) : 2 + (3 · 4 ) : 2 = 20 (см₂) II способ: [(7 + 3) · 2] : 2 = 20 (см₂) Ответ: 20 см₂. 7 см С.124 №11 (б - 1)](https://prezentacii.org/upload/cloud/19/06/155159/images/thumbs/screen13.jpg)
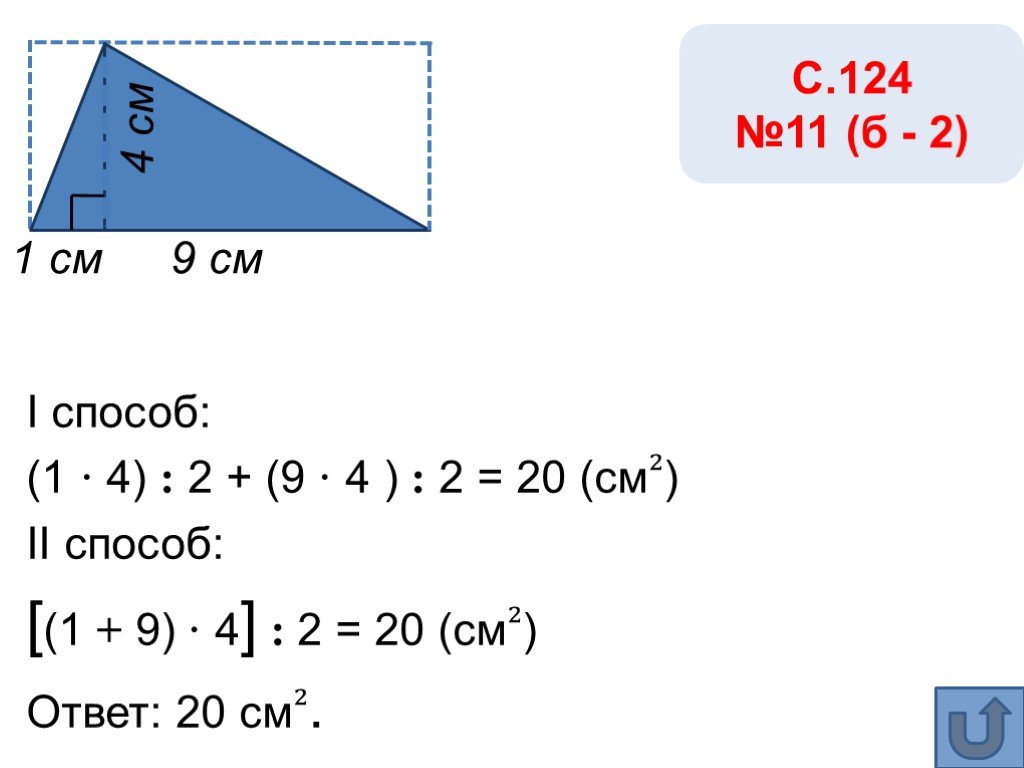
![I способ: (1 · 4) : 2 + (9 · 4 ) : 2 = 20 (см₂) II способ: [(1 + 9) · 4] : 2 = 20 (см₂) Ответ: 20 см₂. 1 см 9 см С.124 №11 (б - 2) I способ: (1 · 4) : 2 + (9 · 4 ) : 2 = 20 (см₂) II способ: [(1 + 9) · 4] : 2 = 20 (см₂) Ответ: 20 см₂. 1 см 9 см С.124 №11 (б - 2)](https://prezentacii.org/upload/cloud/19/06/155159/images/thumbs/screen14.jpg)