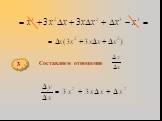Презентация "Основные правила дифференцирования" по математике – проект, доклад

Скачать презентацию (0.26 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Презентацию на тему "Основные правила дифференцирования" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).

Скачать презентацию (0.26 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

8.3. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

Производная функции может быть найдена по схеме:

Дадим аргументу х приращение Δх и найдем значение функции y+Δy=f(x+Δx)

Слайд 2

Находим приращение функции Δy=f(x+Δx)-f(x)

Составляем отношение:

4 Находим

Слайд 3

ПРИМЕР.

Найдем производную функции

Дадим аргументу х приращение Δх и найдем значение функции y+Δy:

1 2

Находим приращение функции

Слайд 4

Составляем отношение

Слайд 5

Полученный результат является частным случаем производной от степенной функции

Можно показать, что в общем случае

Слайд 6

производная степенной функции

Слайд 7

ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

Производная постоянной величины равна 0:

Производная аргумента равна 1:

Слайд 8

Производная алгебраической суммы (разности) конечного числа дифференцируемых функций равна сумме (разности) производных этих функций:

Слайд 9

ДОКАЗАТЕЛЬСТВО:

Пусть u=u(x) и v=v(x) -дифференцируемые функции. Найдем производную функции y=u + v.

Дадим аргументу х приращение Δх, не равное 0, тогда функции получат значения u+Δu, v+Δv.

Слайд 10

Находим предел этого отношения:

Слайд 11

Производная произведения двух дифференцируемых функций равна сумме произведений производной первого сомножителя на второй и производной второго сомножителя на первый:

Слайд 12

Пусть u=u(x) и v=v(x) -дифференцируемые функции. Найдем производную функции y=uv.

Слайд 13

Слайд 14

Имеем по определению производной:

Слайд 15

Следствие 1.

Постоянный множитель можно выносить за знак производной:

Следствие2.

Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные:

Слайд 16

Производная частного двух дифференцируемых функций находится по формуле:

Слайд 17

ПРИМЕРЫ.

Найти производную функции

и вычислить ее значение в точке х=1.

Слайд 18

Решение.

Находим значение производной в точке х=1:

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Список похожих презентаций

Правила дифференцирования

Правила дифференцирования. Цель урока: закрепление знаний и обработка навыков вычисления производной функции; подготовить учащихся к предстоящей самостоятельной ...

Правила дифференцирования

Проверка домашней работы. № 210 а. № 211 а,б,в. Устно. Решение упражнений. № 213 в,г № 214 б,в. Самостоятельная работа. 1 группа 2 группа. . . . . ...

Правила дифференцирования

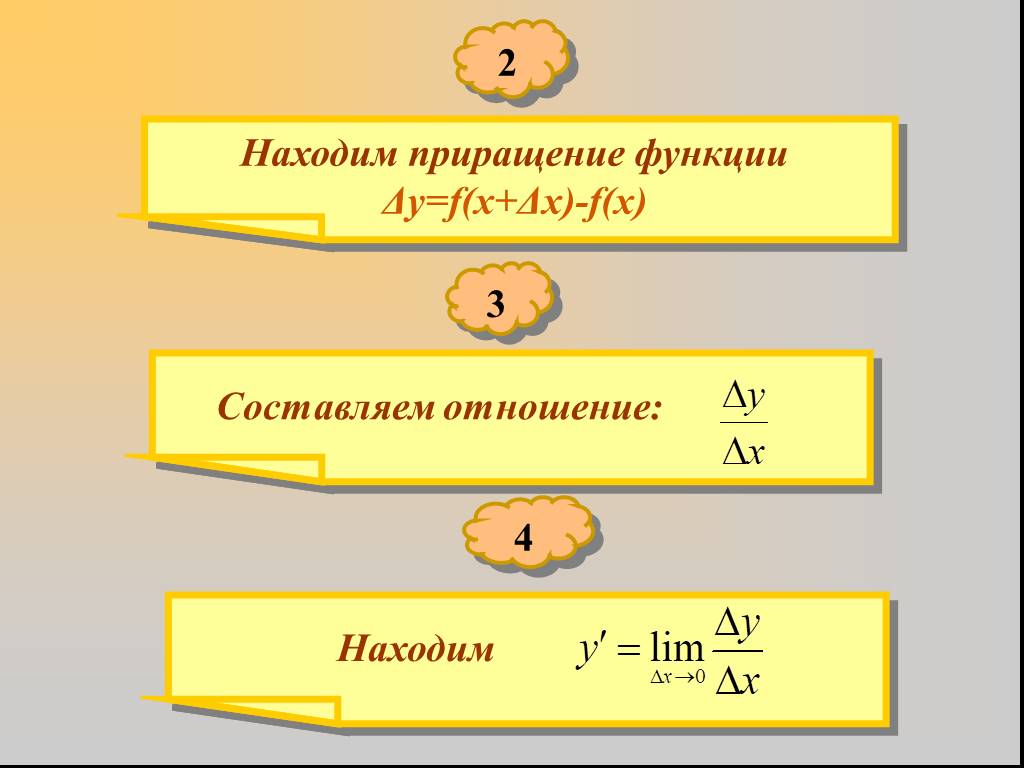
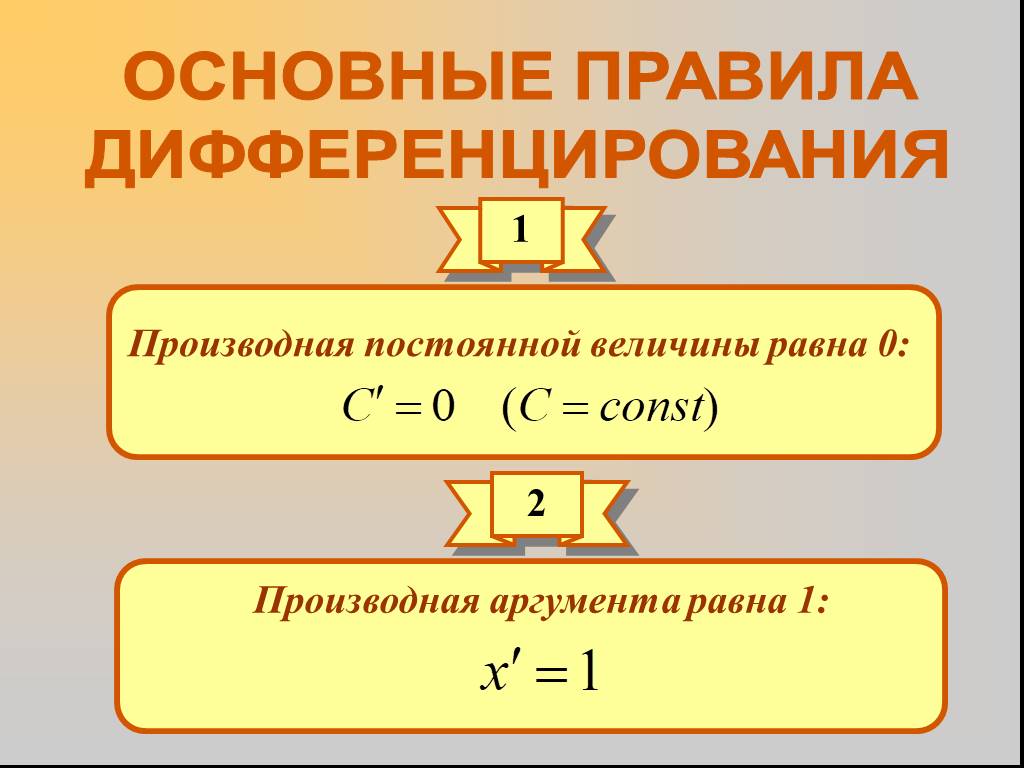
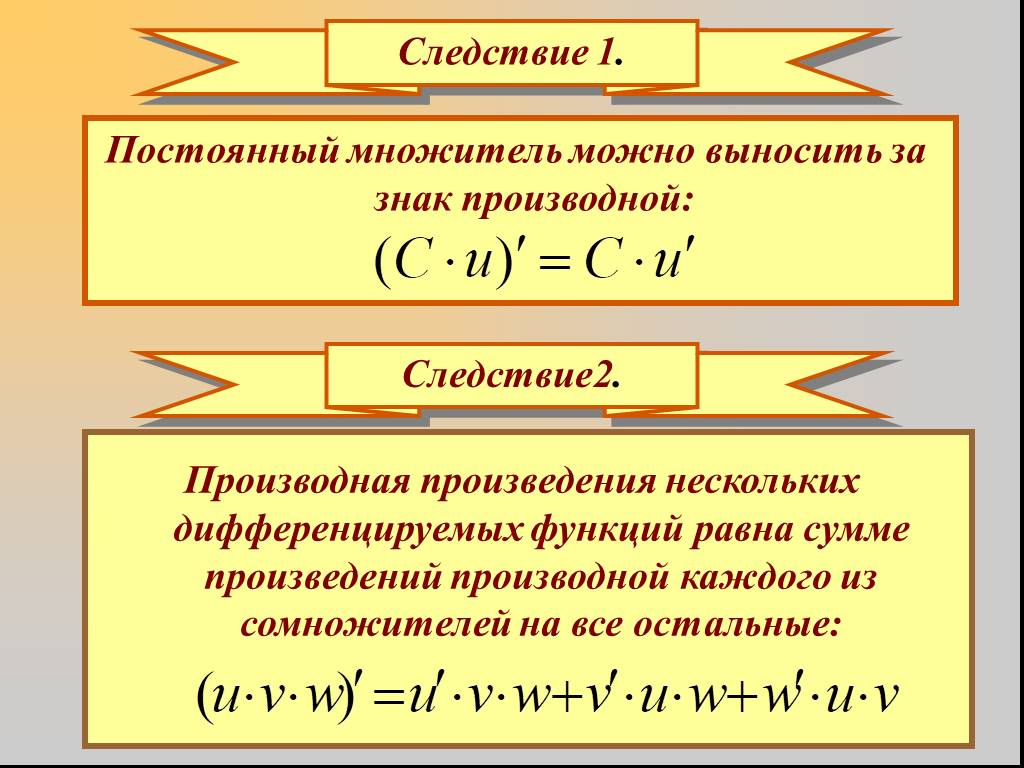
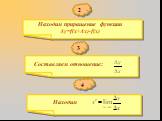
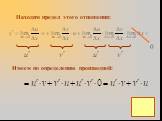
Производная суммы равна сумме производных. Постоянный множитель можно вынести за знак производной. Производная произведения двух функций, равна сумме ...

Правила дифференцирования

Проверка домашней работы. № 198а x y -1. № 200в. Устно. 22.02.2010г. Формулы дифференцирования. Значения функции в данной точке:. Значения производной ...

Теория вероятностей и комбинаторные правила

Классическое определение вероятности. Стохастическим называют опыт, если заранее нельзя предугадать его результаты. Результаты (исходы) такого опыта ...

Основные виды движений

Содержание. 2. Движения относительно точки. 3. Движения относительно прямой. 5. Зеркальная симметрия. 6. Заключение 1. Введение. 4. Параллельный перенос. ...

Системы счисления. Основные определения, виды, свойства

ОПРЕДЕЛЕНИЯ. СИСТЕМА СЧИСЛЕНИЯ - совокупность приемов и правил для записи чисел. Коэффициенты - знаки (цифры), используемые для записи чисел. Наиболее ...

Основные труды и биография Декарта

Рене́ Дека́рт (31 марта 1596, Лаэ (провинция Турень) — 11 февраля 1650, Стокгольм) — французский математик, философ, физик и физиолог, создатель аналитической ...

Основные фигуры в пространстве

Точка A. Прописные латинские буквы A, B, C, D, E, K, …. Прямая a. Строчные латинские буквы a, b, c, d, e, k, …. Плоскость α. Греческие буквы α, β, ...

Основные теоремы теории вероятностей

Литература и интернет - ресурсы. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей: учебное пособие. М.: Академия, 2003. – 448 ...

Основные тригонометрические формулы

Основные формулы тригонометрии и их свойства. Дадим определения тригонометрическим функциям синуса, косинуса, тангенса и котангенса. возьмем любой ...

Основные понятия

В задачах на смеси, растворы и сплавы основными понятиями являются: «концентрация», «процентное содержание», «закон сохранения массы», «закон сохранения ...

Основные понятия дроби

Закрепить понятие алгебраической дроби; Научить составлять математическую модель задачи; Научить находить значение алгебраической дроби, находить ...

Основные задачи на проценты

Как найти 1% от числа? 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти ...

Основные закономерности развития информационного пространства

Правило Парето. Анаизируя общественные процессы, Парето рассматривал социальную среду как пирамиду, наверху которой находятся немногие люди, составляющие ...

Основные задачи на проценты

1. Дробь 1/5 равна А) 20% Б) 30% В) 50%. назад. Может подумаешь еще? . 2. 30% от числа 800 равно. А) 24 Б) 240 В) 2400. . . 3.У нас в школе есть участок ...

Основные задачи на проценты

Представьте данные десятичные дроби в процентах:. 0,5=…% 123=…% 0,045=…% 0,6=…%. 0,0035=…% 0,123=…% 70,5=…% 0,01=…%. 10=…% 1,5=…% 7,2=…% 0,42=…%. ...

Основные задачи на проценты

Как найти процент от числа? Пример1. Например, найдём 18% от 20: 18%=0,18 , 20·0,18=3,6 Пример 2. Найдём 4% от 8: 1 способ: 4%=0,04 , 8·0,04=0,32. ...

Граф и его элементы. Основные определения

Переход по слайдам осуществляется только по нажатию левой кнопки мыши клик мыши!!! Если есть мигающая стрелка, значит нужно нажатие левой кнопки мыши ...

Основные понятия и определения

Основные понятия и определения. Система — объединение элементов, образующих связное целое. Элемент — объект, учитываемый внешними связями и не разлагаемый ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.