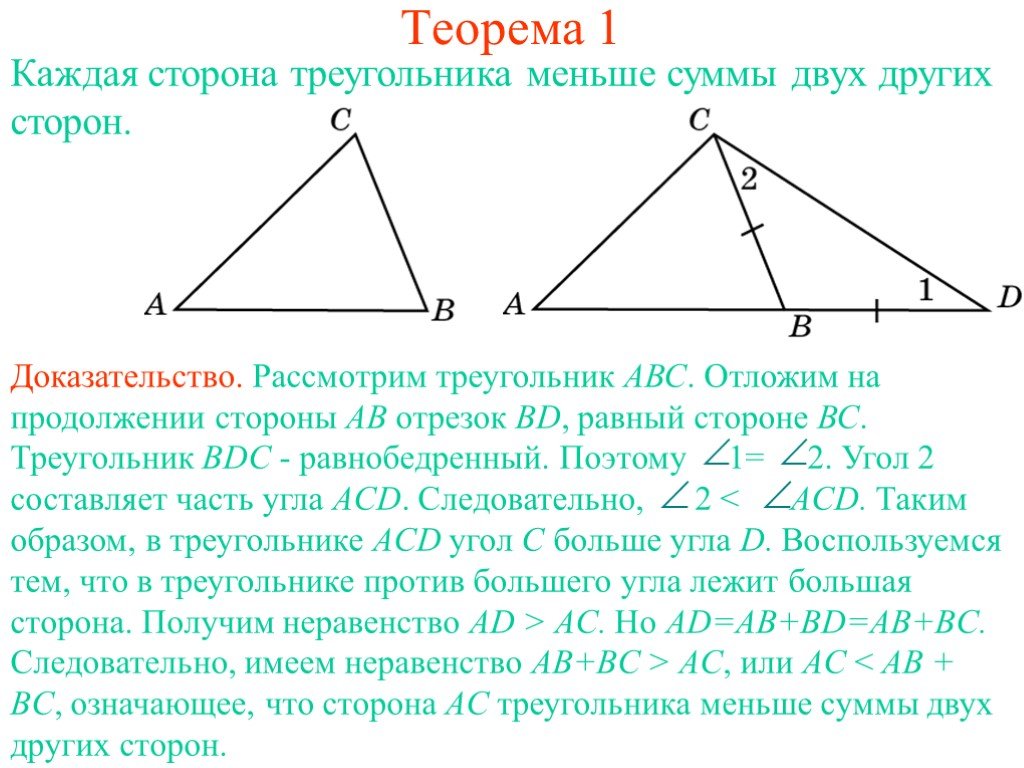
Презентация "Каждая сторона треугольника меньше суммы двух других сторон" по математике – проект, доклад
Презентацию на тему "Каждая сторона треугольника меньше суммы двух других сторон" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Установление соотношения между сторонами и углами прямоугольного треугольника
? Это - ? (какой треугольник). Актуализация. Практическая работа «Установление соотношения между сторонами и углами прямоугольного треугольника» Цель: ...Соотношения между сторонами и углами прямоугольного треугольника
Найти: 1) sinA, 2) cоsA, 3) tg A Ответ: sin A= Ответ: соsA= tg A=. Дано: АВСD – трапеция, АВ = 16 см, ВАD = 30, СDА = 45. Найти: ВК и ...Соотношения между сторонами и углами прямоугольного треугольника
ОТНОШЕНИЕ ПРОТИВОЛЕЖАЩЕГО КАТЕТА К ГИПОТЕНУЗЕ. ТО, ЧТО ВЫРАЖАЕТ ТЕОРЕМА: «ЕСЛИ ДВА УГЛА ОДНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ДВУМ УГЛАМ ДРУГОГО ...Соотношения между сторонами и углами прямоугольного треугольника"
Цели:. формирование умений и навыков в применении соотношений между сторонами и углами прямоугольного треугольника; формирование умений работать с ...Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Вопросы для повторения:. Пропорциональные отрезки: 1. Высота, проведённая из вершины прямого угла на гипотенузу в прямоугольном треугольнике, делит ...Соотношения между сторонами и углами треугольника
Теорема о площади треугольников. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Стороны треугольника пропорцианальны ...Соотношения между сторонами и углами треугольника
Работаем устно ( теоретические сведения). А С В. 1. Назовите фигуру представленную на рисунке. 2. Перечислите названия её составных частей. 3. Укажите ...Соотношения между сторонами угла прямоугольного треугольника
─ Ввести понятие синуса, косинуса, тангенса, котангенса, секанса, косеканса острого угла прямоугольного треугольника. ─Научиться решать прямоугольные ...Периметр треугольника. Построение треугольника по заданным сторонам
1.Классификация треугольников по длинам сторон. Равносторонний треугольник. 4 см 4см. Разносторонний треугольник. 5см 6 см 7 см. Равнобедренный треугольник. ...Построение треугольника по трем сторонам
Цели урока:. Научиться строить треугольник по трем заданным сторонам. Познакомиться с некоторыми ГМТ. Совершенствовать умения по решению задач на ...Возведение в квадрат суммы и разности двух выражений.
«Слабое звено». 1. Вычислите: 52 ; 23; (-5)3 ; (-8)2 ; 112 ; 0,32 ; 1,52. 2. Представьте в виде многочлена: (х+у)2; (m-n)2; (х-5)2; (2х+3)2; (5n+3)2; ...Возведение в квадрат суммы и разности двух выражений
ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ. ТЕМА УРОКА. Образовательные: -вывести формулы квадратов суммы и разности двух чисел; -сформировать ...Возведение в квадрат суммы и разности двух выражений
ЦЕЛЬ: пользуясь правилом умножения многочленов, провести исследовательскую работу и вывести формулы (а±в)²=а²±2ав+в²; привитие навыка самостоятельной ...Возведение в квадрат суммы и разности двух выражений
Из истории Древнего мира. Среди математиков Древней Греции было принято выражать алгебраические утверждения в геометрической форме. Вместо сложения ...Правило вычисления алгебраической суммы двух чисел
Устный счёт. -9+6 = 5+(- 4)= -6+(- 2)= -8+8= 13+(- 4)= 0+(- 7)= 3+(- 3)= -12+10=. - 3 - 8 9 0 1 -7 -3 -8. На координатной прямой числа m и n противоположные ...Стороны и углы прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника. Мама мой взяла листок, И загнула уголок, Угол вот такой у взрослых Называется ПРЯМЫМ. ...Формулы квадрата суммы и квадрата разности двух выражений
Цели:. Систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением формул квадрата суммы и квадрата разности. Содействовать ...Квадрат суммы и квадрат разности двух выражений
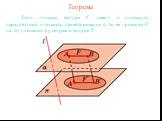
Игра «Третий лишний». 3² 9 6 4а² 16а² (4а)² (а + b)² (a + b)(a + b) a² + b² (c – d)² (c – d)(c + d) (c – d)(c – d) (7 – 3)² 16 40 (– a)² a² – a² (a ...Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы
Пример 1. Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы. Действительно, пусть дан произвольный треугольник ...Свойства равнобедренного треугольника
план урока:. Решение задач по готовым чертежам Виды треугольников по длинам сторон Доказательство теоремы Решение задач Самостоятельная работа. Решить ...Конспекты
Соотношение между сторонами и углами треугольника
Фрагмент урока по теме: «Соотношение между сторонами и углами треугольника» (9 класс, учебник «Геометрия 7 – 9», Л. С. Атанасян). Автор:. учитель ...Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника (8-й класс). Цели:. Совершенствовать. навыки решения прямоугольных треугольников. ...Соотношения между сторонами и углами прямоугольного треугольника
Оноприенко Л.Н.;. . учитель математики ШЛ №27. . (из опыта работы). Урок по теме. : Соотношения между сторонами и углами прямоугольного треугольника. ...Соотношения между сторонами и углами прямоугольного треугольника
МОУ «Лицей №31». Методическая разработка урока. по геометрии в VIII. классе. по проблеме: «Личностно-ориентированный подход ...Соотношения между сторонами и углами прямоугольного треугольника
Конспект урока на тему «Соотношения между сторонами и углами прямоугольного треугольника». 1. Оргмомент. Слайд 1. Здравствуйте. Поднимите ...Соотношения между сторонами и углами треугольника
Общеобразовательная школа I. -III. ступеней №31. Симферопольского городского совета. Республики Крым. Обобщающий урок. по теме. «Соотношения ...Соотношения между сторонами и углами треугольника
Тема урока: «Соотношения между сторонами и углами треугольника». Основные цели урока:. обобщить теоретические знания по теме: «Решение треугольников»;. ...Теорема о соотношениях между сторонами и углами треугольника
Урок геометрии в 7 классе. Тема:. Теорема о соотношениях между сторонами и углами треугольника. Тип урока:. объяснение нового материала. Цели ...Соотношение между сторонами и углами прямоугольного треугольника
Урок по геометрии 8 классе. . «Соотношение между сторонами и углами прямоугольного треугольника». Цели урока:. . образовательная. :. . . ...Возведение в квадрат суммы и разности двух выражений
МКОУ «Гавриловская средняя общеобразовательная школа». Учитель математики Панкратова Нина Владимировна. ПЛАН-КОНСПЕКТ УРОКА ПО АЛГЕБРЕ 7 КЛАСС. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 февраля 2019
Категория:Математика
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию