Презентация "Алгебра «Производные»" – проект, доклад
Презентацию на тему "Алгебра «Производные»" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
Алгебра модуля
АЛГЕБРА МОДУЛЯ. Решение уравнений с модулем. Решение неравенств с модулем. Построение графиков с модулем. Построение с помощью Преобразования графиков. ...Алгебра логики на практике
«Всё наше достоинство заключено в мысли. Не пространство, не время, которых мы не можем заполнить, возвышает нас, она, наша мысль. Будем же учиться ...Алгебра логики. Понятие высказывания
Алгебра логики – часть дискретной математики Математический аппарат алгебры логики широко используется в информатике : Проектирование ЭВМ Теория автоматов ...Ребусы. Алгебра
Гипербола. График. Дискриминант. Квадратное (уравнение). Линейная (функция). Линейное (уравнение). Медиана. Парабола. Переменная. Степень. Уравнение. ...Алгебра
Цель:. - создание условий для ранней психологической адаптации учащихся к переходу на профильное обучение. Гипотеза:. Если скорректировать программу ...Линейная Алгебра
2. Вычислительная линейная алгебра. Основные результаты Методы решения СЛАУ Прямые Итерационные. Теорема Пусть наряду с СЛАУ Au = f рассматриваетмся ...Подготовка к ОГЭ по математике. Алгебра
Цели и задачи. Оказать помощь уч-ся в подготовке к ОГЭ по математике ( базовая часть « Алгебра» Развивать вычислительные навыки; мышление; интерес ...Алгебра и геометрия
История. Женщина обучает детей геометрии. Иллюстрация из парижской рукописи Евклидовых «Начал», начало XIV века. Средние века немного дали геометрии, ...Алгебра и геометрия
Комплексные числа. ׳. Содержание. § 1. Основные понятия § 2. Геометрическое изображение комплексных чисел § 3. Формы записи комплексных чисел § 4. ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Алгебра Геометрическая прогрессия
Девиз урока: «Нельзя быть любознательным с ленцой…». Личностные цели. Самостоятельно добывать знания Уверенно и грамотно выражать свои мысли на математическом ...Алгебра высказываний
ВОПРОСЫ. 1. Что такое логика? Формальная логика. Математическая логика. 2. Этапы развития логики. 3. Применение математической логики. 4. Алгебра ...Алгебра в 9 классе.
Функция их свойства и графики. Сформулируйте определение чётной функции, определение нечётной функции. Не является ни чётной, ни нечётной. чётная ...Алгебра «Многочлены»
Цель урока. Систематизировать и обобщить знания учащихся по теме, развивать навыки самопроверки, внимание , усидчивость, терпение, воспитывать аккуратность ...Алгебра функции
Функции. Задания раздела направлены на проверку умений использовать графические представления для ответа на вопросы , связанные с исследованием функций. ...Алгебра и начала анализа "Логарифмическая функция"
Содержание. Титульный лист Содержание Определение логарифмической функции Свойства логарифмической функции График логарифмической функции Примеры. ...Алгебра функций
Конспект занятия. Учитель Винник Надежда Анатольевна Предмет: Элективный курс по математике «Алгебра функций» Тип занятия: занятие-практикум Тема ...Алгебра и начала анализа 10-11 класс
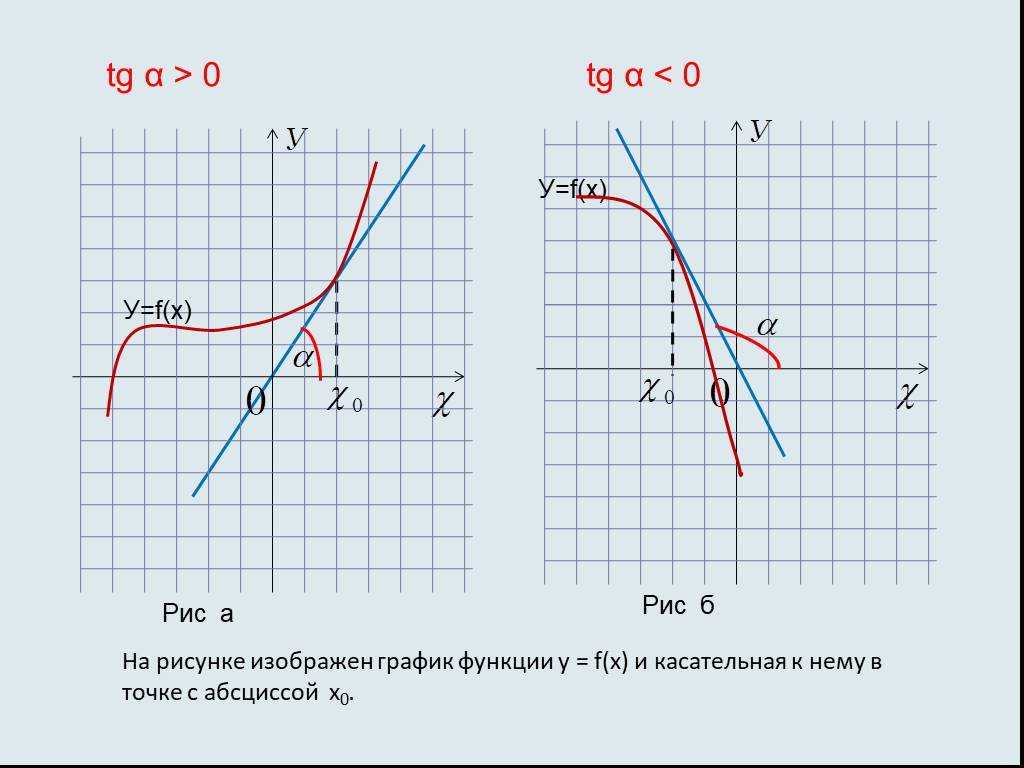
Числовые функции, заданные формулами y=sin x и y=cos x,называют соответственно - ??? и ???. Числовые функции, заданные формулами y=tg x и y=ctg x, ...Основы логики. Алгебра высказываний
Логика. Логика – это наука о формах и способах мышления, позволяющая строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. ...Алгебра и начала математического анализа
УМК "Алгебра и начала анализа" 10 – 11 класс. Профильный уровень. ЦЕЛЬ: Оказать методическую помощь учителям при выборе УМК для работы в профильных ...Конспекты
Алгебра событий и основные правила вычисления вероятностей
Закономерности окружающего мира – 7 класс. Тема 9. Алгебра событий и основные правила вычисления вероятностей. урок на тему. Правило сложения ...Алгебра и начала анализа 10 класс
Алгебра и начала анализа 10 класс(поурочные планы). . 1-е полугодие. . Глава 1. Числовые функции. . Уроки 1-2. Определение числовой функции ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 января 2019
Категория:Математика
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию