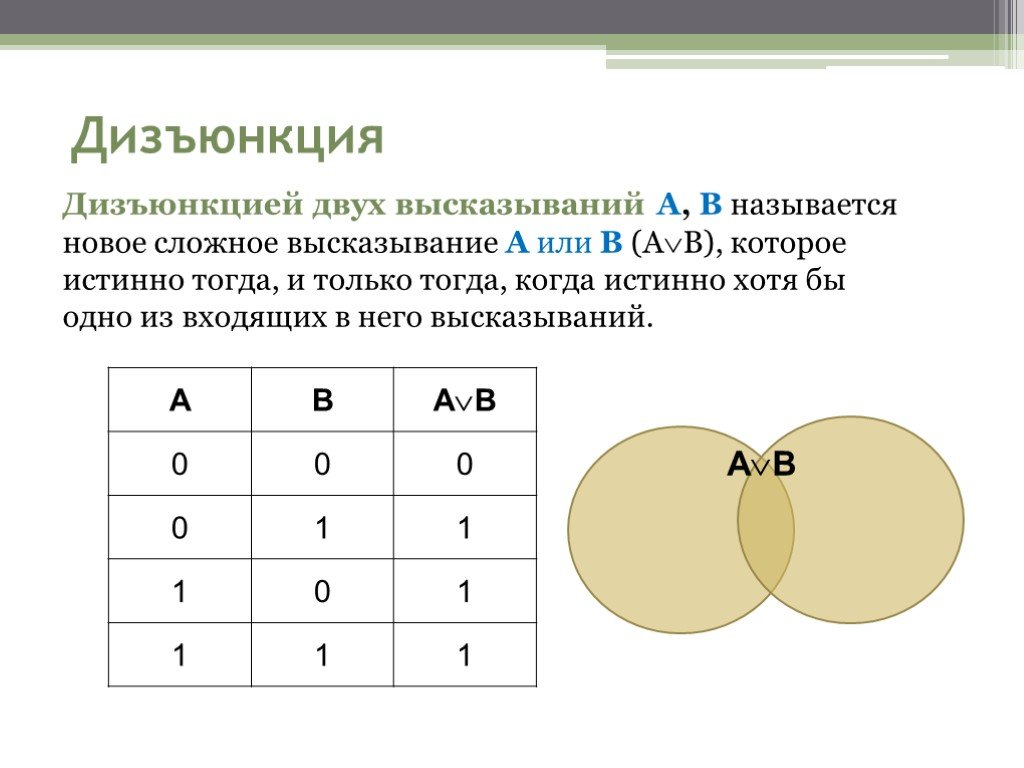
Презентация "Основы логики. Алгебра высказываний" – проект, доклад

Основы логики Алгебра высказываний

Презентация 9-3

Логика

Логика – это наука о формах и способах мышления, позволяющая строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. Это учение о способах рассуждений и доказательств. Мышление всегда осуществляется через понятия, высказывания и умозаключения.

Понятие

Понятие – форма мышления, отражающая наиболее существенные свойства предмета, отличающие его от других предметов. Содержание составляет совокупность существенных признаков. Объем определяет совокупность предметов, на которую понятие распределяется и может быть представлено в форме множества объектов. Наглядное представление – диаграммы Эйлера-Вена.

В А

Высказывание

Высказывание – форма мышления, выраженная с помощью в форме повествовательного предложения, в котором что-либо утверждается или отрицается и относительно которого можно судить истинно оно или ложно. Вопросительные, восклицательные, побудительные предложения и предложения, содержащие переменную, высказываниями не являются. Пример Истинное высказывание: «Буква «а» – гласная». Ложное высказывание: «Компьютер был изобретен в середине XIX века».

Упражнение

Какие из предложений являются высказываниями? Определите их истинность. Какой длины эта лента? Делайте утреннюю зарядку! 4 + 5 = 10. Назовите устройство ввода информации. Париж – столица Англии. Число 11 является простым. Без труда не вытащишь и рыбку из пруда. Сложите числа 2 и 5. Некоторые медведи живут на севере. Все медведи – бурые. Чему равно расстояние от Москвы до Смоленска. 5 < 3.

Умозаключение

Умозаключение – форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам логического вывода получается новое знание о предметах реального мира (вывод). Пример Посылки Все металлы электропроводны. Ртуть является металлом. Вывод Ртуть электропроводна.

Алгебра высказываний

Алгебра высказываний – наука об операциях, аналогичных сложению и умножению, которые могут выполняться над высказываниями. Логическая переменная – это простое высказывание, содержащее только одну мысль. Ее символическое обозначение – латинская буква (например, A, B, P, Q и т.д.). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0). На основании простых высказываний могут быть построены составные высказывания.

Логические операции

Логические операции – логические действия. Рассмотрим логические операции – отрицание, конъюнкция, дизъюнкция. - не ( , ¯ ) отрицание; - и (&, ) конъюнкция; - или () дизъюнкция.

Отрицание

Отрицанием высказывания A называется новое сложное высказывание не A (A ), которое истинно тогда и только тогда, когда A ложно.

A A

Конъюнкция

Конъюнкцией двух высказываний A, B называется новое сложное высказывание A и B (A&B, AB), которое истинно тогда, и только тогда, когда истины оба входящих в него высказывания.

A&B

Дизъюнкция

Дизъюнкцией двух высказываний A, B называется новое сложное высказывание A или B (AB), которое истинно тогда, и только тогда, когда истинно хотя бы одно из входящих в него высказываний.

AB

Логическое выражение

Логическое выражение – формула, содержащая составное высказывание (логическую функцию) и знаки логических операций, значение которой можно вычислить (результат 0 пли 1). При составлении логического выражения необходимо учитывать порядок выполнения логических операций, а именно: действия в скобках; приоритет операций: отрицание, конъюнкция, дизъюнкция.

1. Определите истинность составного высказывания: (A&B)&(C˅D), состоящего из простых высказываний: A = «принтер устройство вывода информации»; B = «процессор – устройство хранения информации»; C = «монитор – устройство вывода информации» D = «клавиатура – устройство обработки информации».

2. Для какого символьного выражения верно высказывание: ¬ (Первая буква согласная)  ¬ (Вторая буква гласная)? 1) abcde 2) bcade 3) babas 4) cabab

3. Для какого из указанных значений числа X истинно выражение (Х > 2) & ((X < 4)  (X > 4))? 1) 1 2) 2 3) 3 4) 4

4. Для какого из указанных значений числа X истинно высказывание (Х < 3) & ¬(X < 2)? 1) 1 2) 2 3) 3 4) 4

5. Для какого названия животного ложно высказывание: В слове 4 гласных буквы  ¬ (Пятая буква гласная)   В слове 5 согласных букв? 1) Шиншилла 3) Антилопа 2) Кенгуру 4) Крокодил

6. Для какого из указанных значений числа X ложно выражение (Х > 2) ИЛИ НЕ(X > 1)? 1) 1 2) 2 3) 3 4) 4

7. Для какого символьного набора истинно высказывание: Вторая буква согласная  (В слове 3 гласных буквы   Первая буква согласная)? 1) УББОШТ 3) ШУБВОИ 2) ТУИОШШ 4) ИТТРАО