Презентация "Трапеция. Свойства трапеции" по математике – проект, доклад

Трапеция. Свойства трапеции

тема урока: Геометрия, 8 класс

Шайдуллина Р.М. 219-912-302

Ответьте на вопросы

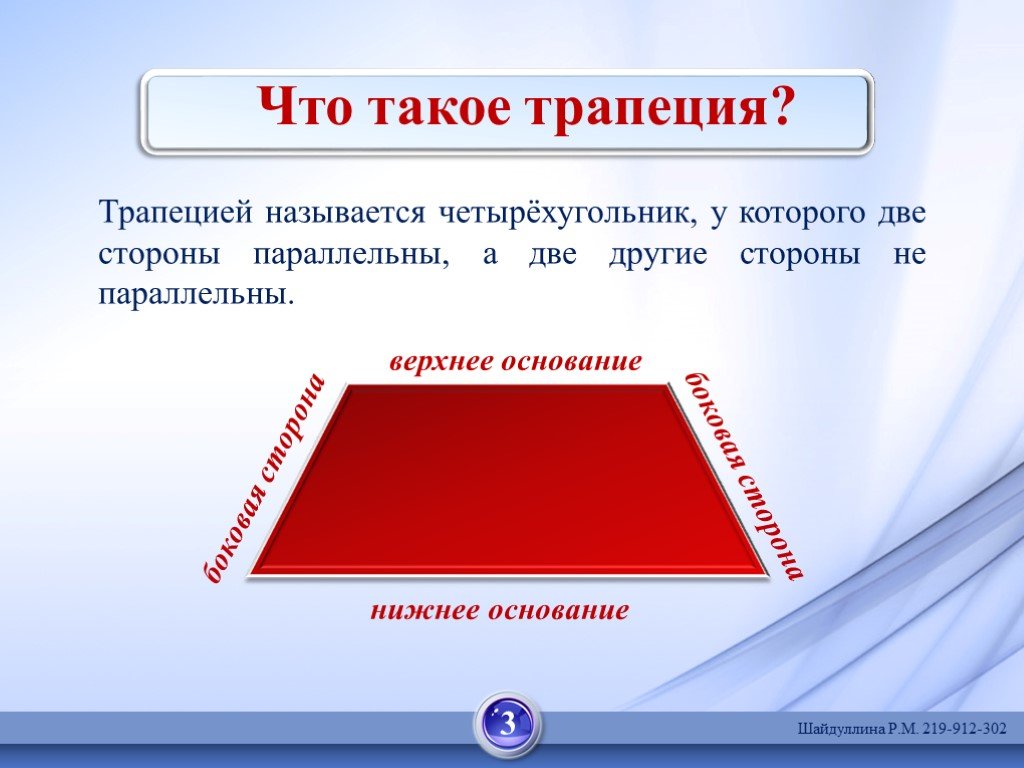
Из чего составлена данная геометрическая фигура? Какими должны быть треугольники, составляющие трапецию? Как составляются треугольники и прямоугольник? А что вы знаете о противоположных сторонах прямоугольника? Значит, и в данном четырёхугольнике будут параллельные стороны? Сколько их?

Что такое трапеция?

Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

верхнее основание

нижнее основание боковая сторона

«Трапеция» - слово греческое, означавшее в древности «столик» (по гречески «трапедзион» означает столик, обеденный стол. Геометрическая фигура была названа так по внешнему сходству с маленьким столом. В «Началах» (греч. Στοιχεῖα, лат. Elementa) — главный труд Евклида, написанный около 300 г. до н. э. и посвящённый систематическому построению геометрии) термин «трапеция» применяется не в современном, а в другом смысле: любой четырехугольник (не параллелограмм). «Трапеция» в нашем смысле встречаются впервые у древнегреческого математика Посидония (Iв.). В средние века трапецией называли, по Евклиду, любой четырехугольник (не параллелограмм); лишь в XVIIIв. это слово приобретает современный смысл.

Происхождение слова « трапеция»

Задание №1 3 4

Проверь себя

ЗАДАЧА №1

Будут ли равны две трапеции, у которых соответственно равны одно из оснований и две боковые стороны?

ВИДЫ ТРАПЕЦИЙ

Связь трапеций с треугольниками

Трапеция называется равнобедренной, если её боковые стороны равны

РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ

ПРЯМОУГОЛЬНАЯ ТРАПЕЦИЯ Трапеция, один из углов которой прямой, называется прямоугольной

СВОЙСТВА ТРАПЕЦИИ

Отрезок, соединяющий середины диагоналей, равен полуразности оснований. У равнобедренной трапеции углы при любом основании равны. У равнобедренной трапеции диагонали равны. У равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой - полуразности оснований.

Докажите, что в равнобедренной трапеции: а) углы при каждом основании равны; б) диагонали равны.

ЗАДАЧА №2

Смотрите внимательно на рисунок в течении 30 секунд

Применение формы трапеции в повседневной жизни

в интерьерах (диваны, стены, навесные потолки); в ландшафтном дизайне (границы газонов, искусственных водоемов, формы камней); в индустрии моды (одежда, обувь, аксессуары); в дизайне предметов повседневного пользования (светильники, чайники, пылесосы с использованием форм трапеции и т.д.); в архитектуре

Интерьер

Ландшафтный дизайн

Архитектура

Одежда, аксессуары

Бытовые предметы

ПРАКТИЧЕСКАЯ РАБОТА

В одной системе координат постройте равнобедренные трапеции по заданным трём вершинам. 1 вариант: (0;1), (0;6), (-4;2), (…;…) и (-6;-5), (4;-5), (-4;-3), (…;…). 2 вариант: (-1;0), (4;0), (6;5), (…;…) и (1;-2), (4;-3), (4;-7), (…;…). Определите координаты четвёртой вершины.

2 вариант X (11; 2), Y (2; 3) X (-3; 5), Y(1; -8) 1 вариант

ЗАНИМАТЕЛЬНАЯ ЗАДАЧА

Сложить трапецию из: а) четырёх прямоугольных треугольников; б) из трёх прямоугольных треугольников; в) из двух прямоугольных треугольников. Выяснить, каким условиям при этом должны удовлетворять данные трапеции.

ПРОВЕРЬ СЕБЯ

ДОМАШНЕЕ ЗАДАНИЕ

п.44, стр. 103 знать определение, элементы трапеции, ее виды, свойства, уметь их доказывать 3. № 388, № 390.

АНКЕТА

1. На уроке я работал… 2. Своей работой на уроке я... 3. Урок для меня показался… 4. За урок я… 5. Мое настроение… 6. Материал урока мне было… 7.Домашнее задание мне кажется…

активно / пассивно доволен / не доволен коротким / длинным не устал / устал стало лучше / стало хуже понятен / не понятен полезен / бесполезен интересен / скучен легким / трудным интересно / не интересно