Презентация "ЭКОНОМИКА ПУБЛИЧНОГО СЕКТОРА" – проект, доклад

Экономика публичного сектора

Лектор Макаров Валерий Леонидович ЦЭМИ РАН

Содержание курса

Предмет курса, коллективные блага, проблема измерения. Закон Вагнера. Виды коллективных и, в частности, публичных благ. Институты. Оптимальный уровень предоставления публичных благ. Соотношение Самуэльсона. Государство как производитель благ. Равновесие по Линдалу. Налоги по Линдалу. Равновесие по Линдалу и ядро. Пример Канеко. Клубные блага. Задача оптимального размера клуба. Задача порождения институтов (клубов, юрисдикций). Локальные публичные блага. Экономика Тибу. Гипотеза Тибу. Примеры не существования равновесия в экономике Тибу. Институциональное и миграционное равновесия. Примеры существования равновесий. Модель двухслойной экономики. Примеры поиска равновесия. Эгалитаризм Тобина. Модель бюрократии Нисканена. Продукты, необходимые для жизни. Регулирование естественных монополий. Модель Буато. Принципы налогообложения. Эффективные по Парето системы налогообложения. Примеры эффективных по Парето систем налогообложения. Федерализм. Оптимальное число уровней для локальных правительств. Оптимальный размер и оптимальное количество стран. Модель Алезины и Сполаоре.

Что есть публичный сектор

1. Публичный сектор. 1.1. Государственные предприятия (федеральной собственности и собственности субъектов Федерации). в том числе 1.1.1. Казенные предприятия 1.1.2. Центральный банк и другие институты инфраструктурного характера 1.2. Бюджетный сектор 1.2.1. Оборона, 1.2.2. Образование, культура и искусство 1.2.3. Здравоохранение, физическая культура и социальное обеспечение 1.2.4. Наука и научное обслуживание 1.2.5. Судебные и правоохранительные органы 1.2.6. Государственное управление (аппарат органов управления) 1.2.7. Жилищно-коммунальное хозяйство; непроизводственные виды бытового обслуживания населения. 1.3. Муниципальные предприятия 1.4. Общественные организации 2. Негосударственный (не публичный) сектор 2.1. Корпоративный сектор 2.2. Частный сектор 3. Домашние хозяйства

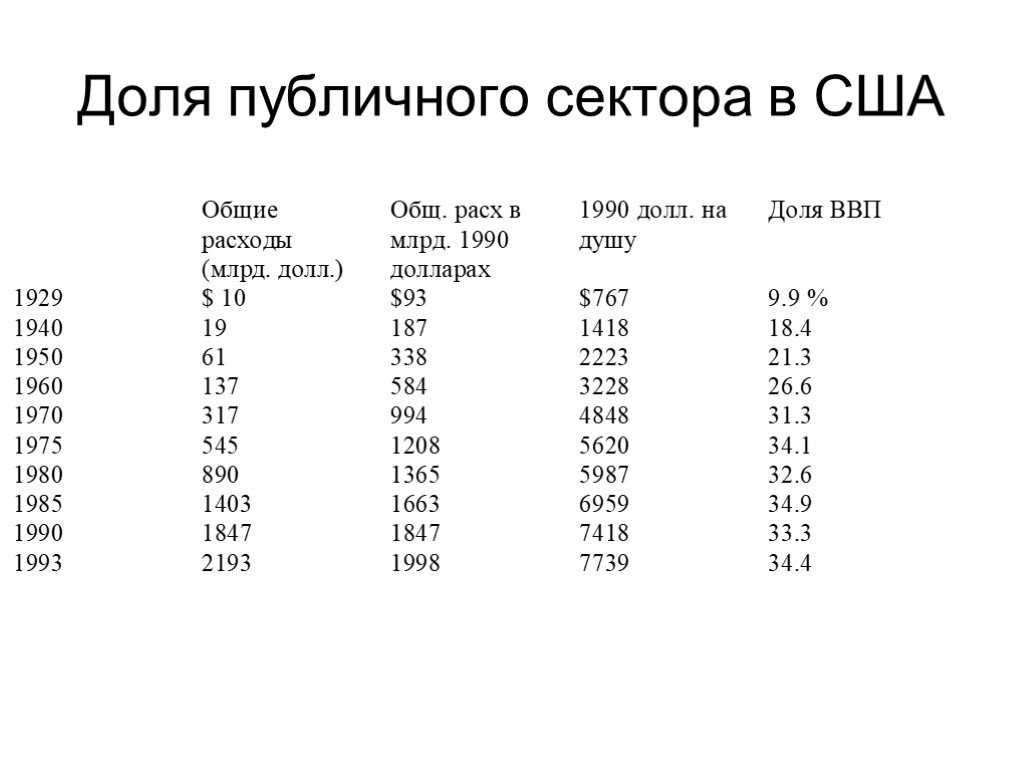
Доля публичного сектора в США

Доля публичного сектора в ВВП по странам (1991г.)

Примеры коллективных благ

Клубные блага (в том числе семейные) Политические блага (политические партии, общественные организации идеологической направленности) Локальные публичные блага (муниципалитет, субъект федерации) Публичные блага (страна) Интернациональные блага (пример, международные организации) Глобальные блага (знания)

Институты первого рода (коалиций граждан)

Клуб Семья Род Фирма Корпорация Общественное объединение Профессиональное объединение Политическая партия Муниципалитет Муниципальный округ Субъект федерации Федеральный округ Государство Союз государств

Институты второго рода (управляющие и прочие органы)

Правительство Парламент Международные организации (ООН, ВТО,…) Дирекция Судебные органы Правоохранительные органы

Институты третьего рода

Социальные нормы Правила, писанные и не писанные. Законы Традиции Ментальность

Многообразие клубов Buchanan, J. M. (1965) Economic Theory of Clubs. Economica, 32, 125, pp.1 - 14.

Фирмы. Государственные, частные, акционерные общества, товарищества, партнерства. Общественные организации. Политические партии, движения, объединения, творческие союзы, ассоциации, Дома ученых, клубы по интересам (филателисты, любители книг), Профсоюзы. Учебные заведения, лечебные учреждения, спортивные общества. Общественные академии наук. Государственные управленческие институты. Министерства, комитеты, агентства, организации муниципалитетов, Это особый тип клубов, которые призваны обслуживать юрисдикции Семья, клан, род, (Племя, повидимому уже относится к юрисдикции по первому признаку). Правило создания: формально зарегистрированный и гражданский браки. Криминальные структуры (мафия). Совокупность подписчиков на журнал, на компьютерную программу. Соответственно это может быть совокупность постоянных посетителей магазина, бара, кинотеатра, которые получают скидки или другие привилегии. Этих людей можно назвать клубом любителей журнала, бара и т.д. Публичный постоянный семинар, научная школа, Постоянные посетители сайта в сети Интернет.

Вопросы для проверки

1. Государственный сектор и публичный сектор – это одно и то же? 2. Придумайте единицы измерения для коллективных благ. 3 Человек потребляет частные и коллективные блага. Как он принимает решение об их потреблении. 4. Почему доля публичного сектора растет со временем (Закон Вагнера)?

Нет. Государственный сектор производит, в основном, частные блага. Рубли, время провождения, штуки… Потребление частного блага – личное решение, потребление коллективного – личное решение о вступлении в институт, а дальше коллективное решение. Усложняются связи в обществе.

Производство коллективных благ

Технически, как правило, нет разницы в производстве частных и коллективных благ. Исключение: процессы производства и потребления совпадают. Математически производство коллективных благ обычно описывается в виде стандартной производственной функции вида g = f(y,L) где g - количество коллективного блага, y -набор частных благ, L - затраты труда.

Соотношение Самуэльсона Samuelson, P. A. (1954) The Pure Theory of Public Expenditure. Review of Economics and Statistics, 37, 4.

В стране имеется N одинаковых граждан и Y = f(N) – производственная функция, где Y есть количество произведенного продукта в стране. Для простоты будем полагать, что частное благо x, и общественное благо g делаются из Y одинаково, то –есть продукт просто направляется либо на частные, либо на общественные нужды. Функция полезности гражданина есть u(x, g). Оптимальное количество благ обоих видов определяется из задачи: max u(x, g) при Y – g = x*N Условие первого порядка, u’(x,g)=u’(x,g)*N; говорит о том, что предельная полезность публичного блага, помноженная на число агентов, равна предельной полезности частного блага. Это и есть соотношение Самуэльсона.

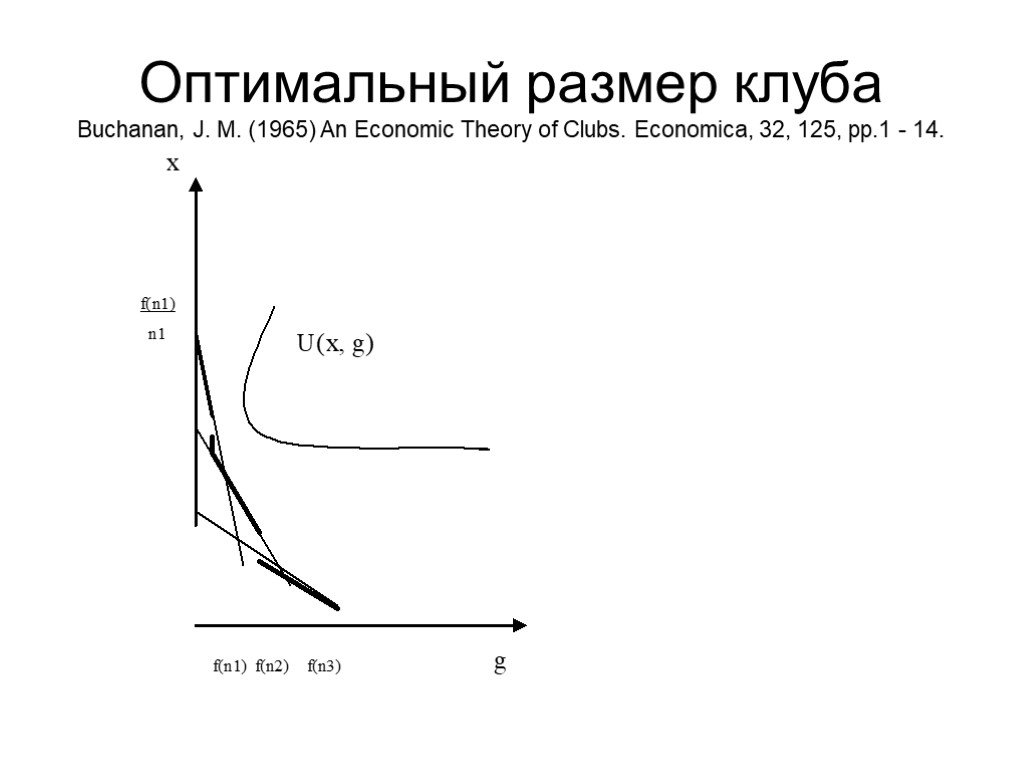
Оптимальный размер клуба Buchanan, J. M. (1965) An Economic Theory of Clubs. Economica, 32, 125, pp.1 - 14.

Затраты потребителя на получение коллективного блага.

Членский взнос Налог Сбор на получение блага

НАЛОГ в задаче Самуэльсона Y - суммарный продукт w=Y/N каждому поровну t налог x=w-t Частное потребление g=t*N публичное благо

Функции институтов первого рода и, частично, второго рода

Принятие коллективных решений Производство коллективных благ Потребление коллективных благ Выполнение заранее сформулированных целей (получение прибыли, реализация проекта, выполнение предписанных функций)

Пример жилого дома Ввести или не ввести наблюдательный пост в доме. Собрать взносы и нанять консьержку. Получать удовольствие от наличия поста.

Механизмы формирования взноса (налога)

Равновесие по Нэшу Shitivitz B. and Spiegel M. “Stable Provision vs. Cournot – Nash Equilibria in Pure Public Good Economies” (2001) Journal of Public Economic Theory 3(2)

Е – экономика N – количество разных потребителей x - количество частного блага g – количество публичного блага wi - бюджет потребителя (члена клуба) i. ui(xi,g) - функция полезности потребителя i. Бюджетное ограничение xi + gi = wi Производство публичного блага g = ∑gi Равновесие по Нэшу (g*i)i=1,..,N ui(x*i,g*) = max ui(wi-gi, ,g*lgi)

Литература на русском языке

Аткинсон Энтони Б. Стиглиц Джозеф Э. (1995) Лекции по экономической теории государственного сектора”, Изд. Аспект Пресс, 1995. Брюммерхофф Дитер (2002). Теория государственных финансов. Пионер-пресс. Бьюкенен Джеймс. (1997) Избранные труды в серии «Нобелевские лауреаты по экономике». Конституция экономической политики (Нобелевская лекция), Расчет согласия (совместно с Таллоком) и Границы свободы. Изд. Таурус Альфа 1997г. Макаров В. Л. (2003) Исчисление институтов. Экономика и математические методы, т. 40, № 2. Стиглиц Дж. Ю. (1997) “Экономика государственного сектора” Изд. Московского университета 1997, ИНФРА-М 1997. Якобсон Лев Ильич, (1996) «Экономика общественного сектора», Основы теории государственных финансов. Учебник для ВУЗов, АСПЕКТ пресс, Москва 1996г. (Есть 2-е издание). Нуреев Р. М. (2005) Теория общественного выбора. Курс лекций. ГУ ВШЭ.

Публичные блага в модели Эрроу – Дебре (1)

Частные блага: k = 1,2,…,K, RK. Публичные блага: g. Производители: j = 1,2,…,J; Yj Потребители: I = 1,2,…,I; Xi , wi, ui(xi,g) Государство: g = g(y) Цены: p = (p1,p2,…,pK) Отношение собственности θij Цены (налоги) по Линдалю: ti

Публичные блага в модели Эрроу – Дебре (2)

Определение. Физическое состояние экономики z = (x1,…, xn,y1,…, ym,y,g) называется сбалансированным, или допустимым, если (1) yj Yj для всех j, xi Xi ; g G; (2) g = g(y) (3) ∑xi + y(g) = ∑yj + ∑wi Состояние (z*,p*,t*) называется (рыночным) равновесием, если (a) z* - cбалансировано, (b) ui(xi*,g*) = max ui(xi,g*), xip* <= wip* + ∑yj*p* θij – ti*g* (c) yj*p* = max yjp*, yj Yj (d) y*p* = ∑ ti*g*

Публичные блага в модели Эрроу – Дебре (3)

Принципы налогообложения

Принцип эквивалентности (benefit principle), когда каждый гражданин оплачивает услуги, предоставляемые государством, в форме налогов.[1] Принцип способности платить (ability-to-pay principle), когда каждый налогоплательщик выплачивает налоги пропорционально своим способностям (благосостоянию). При этом налоговая система преследует две основные цели: Фискальную, когда налоги собираются для финансирования государственных функций (армия, образование, и т.д.); Стимулирующую, когда введение тех или иных налогов способствует подавлению или стимулированию какой-либо деятельности (например, уменьшение ставки налога на прибыль, если она инвестируется в научно-исследовательский (R&D) сектор). [1] На практике такая система налогообложения приводит к слишком большому количеству налогов за каждую предоставляемую услугу.

Простая экономика с ценами по Линдалю и не сводимыми интересами государства (1)

N – количество граждан в экономике x - количество частного блага g – количество публичного блага u(x,g) = √x + g - функция полезности потребителя ug(g) = 2g функция полезности государства w = 1 количество частного блага у каждого. Y = N суммарное количество частного блага. p – цена частного блага, играющая роль нормировки t – цена публичного блага для гражданина, одинаковая для всех tg - цена публичного блага для государства s - величина прибыли государства

Простая экономика с ценами по Линдалю и не сводимыми интересами государства (2)

Равновесие по Линдалю:

Модель Стиглица Регулирование налогами социальной функции государства (1)

Экономика Эрроу - Дебре Y – множество производственных возможностей; ui(ci) – функция полезности i-го агента; wi – начальные запасы i-го агента. (y*,(ci*),p*) рыночное равновесие (ai*) - веса функции благосостояния ∑ ai*ui(ci) при которых максимум достигается в рыночном равновесии Проблема бедных

Модель Стиглица Регулирование налогами социальной функции государства (2)

Проблема: найти такую функцию налогообложения (ti(pw1,…,pwN)) чтобы ai(t1,…,tN) = ai При этом ∑ ti(pw1,…,pwN) = 0 Бюджетные ограничения: cip <= wip - ti(pw1,…,pwN) Пример: кусочек российской налоговой системы. ti(pw1,…,pwN) = 0.13(pwi - p ∑wi/N))

Конкуренция между институтами.

Между юрисдикциями за: (1) население, (2) инвестиции, (3) рейтинг (4) качество жизни, эффективность. Между странами: за лидерство в различных областях. Между университетами: (1) за студентов (количество), (2) за качество услуг, (3) за объем продаж. Между клубами: (1) за престиж (рейтинг), (2) за привлечение нужных людей, (3) за экономическую эффективность (прибыль, минимальные взносы).

Конкуренция между институтами. Модель Тибу Caplin Andrew and Nalebuff Barry, (1997) “Competition among Institutions”, Journal of Economic Theory, 72, pp. 306 – 342, #2, February, 1997.

Имеется конечное число юрисдикций j = 1, 2, ..., J. Для каждой юрисдикции задана производственная функция Fj(Tj) = Gj значение которой показывает количество Gj произведенного локального публичного блага в юрисдикции j, если собранные с граждан налоги составляют величину T. Имеется также конечное число граждан i = 1, 2, …, N, которые расселяются по юрисдикциям. Расселение задается матрицей [ Vij], Если Vij = 1, то человек i живет в юрисдикции j. Тогда во всех остальных юрисдикциях это число равно 0. ui(Gj, Tj) – функция предпочтения гражданина I, где Tj – налог, который гражданин должен платить в юрисдикции j. Задача Тибу При фиксированных ставках налогов люди расселяются по юрисдикциям в зависимости от своих индивидуальных предпочтений при условии совершенной мобильности и полной информированности. Гипотеза Тибу Такое расселение является оптимальным.

Миграционное равновесие

Имеется два города, в которых живут одинаковые люди с функцией полезности: u(x,N) =x/N Миграционное равновесие при N1 = N2 Миграционное равновесие обеспечивает оптимум функции благосостояния (если существует) Равновесие не существует, если N нечетно (например равно трем)

Ещё пример не существования равновесия

Пример не существования равновесия (Bewley, 1981). Пусть существует два типа людей: 2/3 - количество людей первого типа (желтые), - 1/3 количество людей второго типа (белые). Люди первого типа имеют единицу начального запаса частного блага первого типа (земли):.w1=11 Люди второго типа обладают единицей другого начального блага w 2=1 (интеллектом): . Функция полезности следующая: . U(x1,x2,g)=g Производственные функции для общественного блага следующие: , где - затраты частного блага k, - доля населения типа i в общине j. Хотя в равновесии возможны две ситуации: 1), 2) или , тем не менее, оно все равно почему-то не получается. Многие исследователи любили придумывать примеры, когда равновесие либо не существует, либо не лежит на Парето границе. Вообще говоря, правительство в приведенной выше модели старается максимизировать количество людей в регионе. Однако, набирая побольше людей, оно уменьшает общественное благо. В результате получается . Утверждается, что обязательно найдется агент, который захочет перебежать.

Существование миграционного равновесия при смешанном гражданстве

Разделим время пребывания в общине на три равные части. Люди могут составить расписание пребывания в каждой общине, например, таким образом, что каждый живет 1/3 времени в одиночку, а остальное время вдвоем. Тогда каждый получит значение целевой функции равное 1/3 + 1/6 + 1/6 = 2/3. Здесь первое слагаемое есть значение целевой функции на трети времени, когда человек живет один, второе и третье слагаемые – значения целевой функции в оставшихся двух третях времени.

Пример (Эволюция городов).

Пусть в начальном состоянии эволюционного процесса имеется n городов, где через N1,…,Nn обозначена численность населения в этих городах. Предполагается, что все люди в стране одинаковы, то – есть имеют одну и ту же функцию полезности u(x,g) = k*x + g где x -количество частного блага; g - количество публичного блага; k - коэффициент сравнения частного и публичного благ; Каждый человек имеет начальное количество частного блага равное 1. Количество публичного блага в городе i есть gi = ti*Ni , где ti есть уровень налога в городе i. Тогда значение функции полезности гражданина в городе есть k * (1-ti ) + Ni * ti = k + (Ni – k)*ti. Таким образом, имеет место барьер между городами в зависимости от их численности. Города с численностью меньше или равной k попадают в один класс, а все остальные - в другой. Если второго класса нет, то люди мигрируют в меньший город с меньшими налогами. Если второй класс существует, то люди выбирают большой город с большими налогами.

Рыночное создание клуба (1) Ellickson B., Grodal B., Scotchmer S., and Zame W. R., (1999), Econometrica, Vol 67, #5, September 1999, pp 1185 – 1217.

Имеется экономика, в которой число агентов равно 5. Имеется одно частное благо (например, деньги), так что начальное состояние каждого агента равно wa = 2, 4, 6, 8, 10 (по порядку) . Имеется всего одна юрисдикция, где все агенты живут. Каждый агент может участвовать в создании только одного клуба или вообще не участвовать в создании клубов. Стоимость создания клуба равна 6. Функция полезности у всех агентов одна и та же и есть u(x;0) = x , если участник потребляет только частное благо и u(x;n) = 4x/n если он/она является членом клуба, в котором n членов.

Рыночное создание клуба (2)

Для создания клуба нужно 6 единиц частного блага x, qn = 6/n – это плата за членство в клубе, u(wa - qn, n) = 4/n (wa - 6/n). n=0 u= wa n=1 u=4 wa -24 n=2 u=2 wa -6 n=3 u=4/3 wa - 8/3 Равновесное распределение по клубам следующее: 0 wa  6 n=0 бедные не вступают в клубы, 6 wa  9 n=2 средний класс создает клубы по 2 человека, 9 wa 10 n=1 богатые создают клубы по 1 человеку.

Взаимодействие юрисдикций (1) Оптимальное количество стран Alesina Alberto and Spolaore Enrico (1997), On the Number and Size of Nations, The Quarterly Journal of Economics, CXII, #4, November 1997, pp1027-1056.

a - номер произвольного агента (гражданина) [0,1] – множество всех агентов (людей в мире) Функция предпочтения агента a ua(la,ta) = g(1 – αla) + w – ta где w - доход агента (одинаковый для всех) ta - налог la - публичное благо (расстояние до столицы) g - максимальное значение публичного блага, получаемого агентом, если он живет в столице α - коэффициент, показывающий потерю в полезности, когда агент находится на некотором расстоянии от столицы

Взаимодействие юрисдикций (2) Оптимальное количество стран Задача социального плановика

Найти максимум функции благосостояния ∫ ua(la,ta)da при ограничении ∫ tada = Nk где k - затраты на поддержание функционирования правительства Путем несложных рассуждений авторы показывают, что решение данной задачи таково: Все страны имеют одинаковый размер (по числу граждан) и оптимальное число стран равно N* = √g α / 4k в случае, когда целое число. В противном случае это число равно ближайшему к целому числу. При этом правительство располагается ровно в средине страны.

Взаимодействие юрисдикций (3) Деление страны на две части

Пример. Население страны представлено в виде отрезка [0,1]. Оно (население) делится на два типа. Люди, принадлежащие к первому типу, предпочитают жить в маленькой стране, а ко второму типу – в большой. Функция полезности людей первого типа: u(x,r) = x/r; второго типа: u(x,r) = x*r, где x – количество блага, r – размер страны. (Можно r интерпретировать как собранные налоги при условии, что налоговая ставка фиксирована).

Взаимодействие юрисдикций (4) Деление страны на две части

Равновесие. │ l │ 0 0.4 1 Устойчивое равновесие при исходном неравенстве населения и большем количестве любителей жить в большой стране. Неустойчивое равновесие при равенстве стран по населению и большем количестве людей, предпочитающих маленькую страну. Вопрос. Каковы правила деления этой страны на две части?

Взаимодействие юрисдикций (5) Деление страны на две части

Правило (прямого) референдума. Близорукое поведение. Стратегическое поведение.

Двухслойная экономика (1)

Движение: «Двухэтажная экономика» План и рынок. Miyamoto K. Dual - Track System in Transitional Economies. Bull. Univ. Osaka v.40, pp. 25 -31, 1996. Koo, Antony Y.C and Obst, Norman P. “ Dual - Track and Mandatory Quota in Cnina’s Price Reform” Comparative Economic Studies, Vol. 37, No1, pp 1 -17 1995. Makarov V. L. Dual Economy in Russia Today. THE ECONOMIC REVIEW, vol 45, N 2, 1994, pp 117 - 125. Hitotsubashi University, Kunitachi, Tokyo, Japan.

Двухслойная экономика (2)

Tobin, J. (1970) “On limiting the domain of inequality” Journal of Law and Economics, 263-277. Карточная система. Льготы. Альтернатива программам социального обеспечения (См. модель Стиглица) В рамках модели Эрроу-Дебре вводится функция рационирования (у), где у – некий набор продуктов, и (у) –количество продуктов каждому агенту в рамках нормы, (у)= (1(у),2(у),…,k(у)), где i(у) количество i-го продукта, достающееся агенту. Тогда Ui(x1i,x2) – функция полезности i-го потребителя, где x1i – набор продуктов отпускаемый потребителю в рамках нормы, x2 – набор продуктов, покупаемый потребителем на рынке Задача потребителя: Ui(x1i,x2) max, при условиях: x1i q + x2p  wip (бюджетное ограничение) x1i  (у) , где y = yi + wi (физическое ограничение) где р – рыночные цены, q – цены рационирования.

Двухслойная экономика (3)

Дискриминационные цены в экономике знаний. (DRI) Три уровня цен для электроэнергии: (1) регулируемые; (2) контрактные; (3) спотовые; Здравоохранение, образование Корпоративные цены для своих Скидки постоянным покупателям.

Вопросы(1)

Коллективные блага. Примеры коллективных благ, перечислите (побольше) Каковы различия между частными и коллективными благами Кто производит коллективные блага и как, кто их потребляет Статистика публичных благ, закон Вагнера. Институты Что такое институт (включая примеры) Оптимальное предоставление публичного блага (Соотношение Самуэльсона) Оптимальный размер института (клуба) Задача Бьюкенена.

Вопросы(2)

Принятие решений институтом Равновесие по Нэшу Налоги (взносы) по Линдалю Налоги, решающие социальные задачи (Модель Стиглица) Основные функции налогов и взносов. Конкуренция между институтами. За что конкурируют институты? Модель Тибу, гипотеза Тибу. Миграционное равновесие. Смешанные стратегии.

Вопросы(3)

Порождение и преобразование институтов Примеры порождения клубов в условиях рынка. Оптимальное количество и оптимальный размер стран Механизмы деления или слияния стран.