Урок для 8 класса на тему «Симметрия. Виды симметрии»

Содержание

Введение ……………………………………………………………..……3

1. Симметрия в математике …………………………………………….5

2. Симметрия в русском языке…………………..…………….……….10

3. Симметрия в биологии………………………………………………..11

4. Симметрия в искусстве ……………………………………………….13

Заключение………………………………………………………………...16

Использованная литература…………………………………………….17

Симметрия является той идеей, посредством

которой человек на протяжении веков пытался
постичь и создать порядок, красоту и совершенство”.

Г. Вейль

Введение

Цель:

познакомиться с различными видами симметрии

Задачи:

1. дать определение симметрии

2. рассмотреть применение симметрии в различных сферах деятельности человека

3. рассмотреть задачи на применение симметрии

Понятие симметрии проходит через всю многовековую историю человеческого творчества. Многие народы с древних времён владели представлением о симметрии в широком смысле - как эквиваленте уравновешенности и гармонии.

Формы восприятия и выражения во многих областях науки и искусства, в конечном счёте, опираются на симметрию, используемую и проявляющуюся в специфических понятиях и средствах, присущих отдельным областям науки и видам искусства.

Симметрия (от греческого symmetria - "соразмерность") - понятие, означающее сохраняемость, повторяемость, "инвариантность" каких-либо особенностей структуры изучаемого объекта при проведении с ним определенных преобразований.

Симметрия — неизменность при преобразованиях, например, сферическая симметрия тела означает, что его вид не меняется при любом вращении; двусторонняя (зеркальная) симметрия означает, что вид не меняется при отражении и т.п.

Действительно симметричные объекты окружают нас буквально со всех сторон, мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность. Симметрия противостоит хаосу, беспорядку. Получается, что симметрия – это уравновешенность, упорядоченность, красота, совершенство.

Весь мир можно рассмотреть как проявление единства симметрии и асимметрии. Асимметричное в целом сооружение может являть собой гармоничную композицию из симметричных элементов.

Симметрия многообразна, вездесуща. Она создает красоту и гармонию.

1. СИММЕТРИЯ В МАТЕМАТИКЕ.

Идея симметрии часто является отправным пунктом в гипотезах и теориях учёных прошлых веков, веривших в математическую гармонию мироздания и видевших в этой гармонии проявление божественного начала. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна. В своих размышлениях над картиной мироздания человек с давних времен активно использовал идею симметрии. Древние греки полагали, что Вселенная симметрична просто потому, что симметрия прекрасна. Исходя из соображений симметрии, они высказали ряд догадок. Так, Пифагор (5 век до н.э.), считая сферу наиболее симметричной и совершенной формой, делал вывод о сферичности Земли и о ее движении по сфере. При этом он полагал, что Земля движется по сфере некоего «центрального огня». Вокруг того же «огня», согласно Пифагору, должны были обращаться известные в те времена шесть планет, а также Луна, Солнце, звезды.

Широко используя идею симметрии, ученые любили обращаться не только к сферической форме, но также к правильным выпуклым многогранникам. Еще во времена древних греков был установлен поразительный факт – существует всего пять правильных выпуклых многогранников разной формы. Симметрии геометрических тел большое значение придавали греческие мыслители эпохи Пифагора. Они считали, что для того, чтобы тело было "совершенно симметричным", оно должно иметь равное число граней, встречающихся в углах, и эти грани должны быть правильными многоугольниками, то есть фигурами с равными сторонами и углами. Впервые исследованные пифагорейцами, эти пять правильных многогранников были впоследствии подробно описаны Платоном. Древнегреческий философ Платон придавал особое значение правильным многогранникам, считая их олицетворением четырёх природных стихий: огонь-тетраэдр (вершина всегда обращена вверх), земля-куб (наиболее устойчивое тело), воздух-октаэдр, вода-икосаэдр (наиболее "катучее" тело). Додекаэдр представлялся как образ всей Вселенной. Именно поэтому правильные многогранники называются также телами Платона.

Простейшими видами пространственной симметрии являются центральная, осевая, зеркально- поворотная и симметрия переноса.

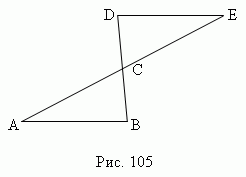
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ.

Геометрическая фигура ( или тело ) называется симметричной относительно центра C ( рис.1 ), если для каждой точки A этой фигуры может быть найдена точка E этой же фигуры, так что отрезок

AE проходит через центр C и делится в этой точке пополам ( AC = CE ). Точка C называется центром симметрии.

ОСЕВАЯ СИММЕТРИЯ

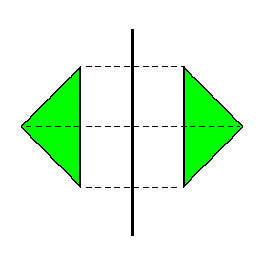
Преобразование фигуры F в фигуру F₁, при котором каждая ее точка переходит в точку, симметричную относительно данной прямой, называется преобразованием симметрии относительно прямой а. Прямая а называется осью симметрии.

.

ЗЕРКАЛЬНО-ПОВОРОТНАЯ СИММЕТРИЯ

Если во внутрь квадрата вписать с поворотом другой квадрат, то это и будет пример зеркально-поворотной симметрии. Если тело можно мысленно пересечь плоскостью так, что каждой точке a тела с одной стороны плоскости будет соответствовать точка b , лежащая по другую сторону плоскости и при том так, что прямая ab, соединяющая эти две точки, перпендикулярна плоскости и делится этой плоскостью пополам, то это тело обладает зеркальной симметрией. Кроме зеркальной симметрии, тела могут обладать еще поворотной симметрией. Тело обладает поворотной симметрией, если при повороте на соответствующий угол все части фигуры совмещаются друг с другом. Ось, вокруг которой происходит вращение тела, называют осью симметрии.

ПЕРЕНОСНАЯ СИММЕТРИЯ

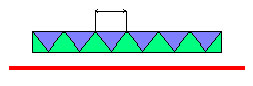
Если при переносе плоской фигуры F вдоль заданной прямой АВ на расстояние а (или кратное этой величине) фигура совмещается сама с собой, то говорят о переносной симметрии. Прямая АВ называется осью переноса, расстояние а элементарным переносом или периодом.

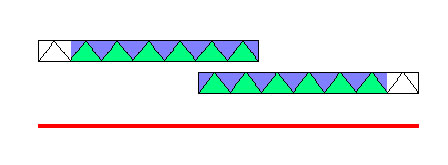
СИММЕТРИЯ ВРАЩЕНИЯ

Тело ( фигура ) обладает симметрией вращения ( рис.106 ), если при повороте на угол 360n  ( здесь n – целое число ) вокруг некоторой прямой AB ( оси симметрии ) оно полностью совпадает со своим

н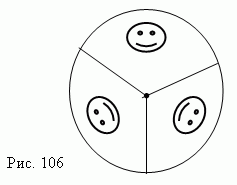ачальным положением. При n = 2 мы имеем  осевую симметрию. Треугольники имеют также осевую симметрию.

ПРИМЕРЫ ВЫШЕУПОМЯНУТЫХ ВИДОВ СИММЕТРИИ

Шар ( сфера ) обладает и центральной, и зеркальной, и симметрией вращения. Центром симметрии является центр шара; плоскостью симметрии является плоскость любого большого круга; осью симметрии – диаметр шара.

Круглый конус обладает осевой симметрией; ось симметрии – ось конуса.

Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.

1.Начертите окружность и определите, как проходит ось симметрии. Сколько осей симметрии имеет окружность?

2.Начертите квадрат, прямоугольник, равнобедренный и равносторонний треугольник. Имеют ли эти фигуры ось симметрии и сколько осей?

3.y = x², y = x³ .Изобразите схематично графики функций. Обладают ли графики этих функций свойством симметрии?

4. Заполните свободные части рисунков числами и фигурами, учитывая вид симметрии (осевая или центральная) и формулы для вычислений.

2. СИММЕТРИЯ В РУССКОМ ЯЗЫКЕ

Буквы А, М, Т, Ш, П имеют вертикальную ось симметрии

А М Т Ш П

В, З, К, С, Э, В, Е – горизонтальную.

В З К С Э Е

А буквы Ж, Н, О, Ф, Х имеют по две оси симметрии.

Ж Н О Ф Х

Симметрию можно увидеть и в словах: казак, шалаш.

КАЗАК ШАЛАШ

Есть и целые фразы с таким свойством (если не учитывать пробелы между словами): “Искать такси”, “Аргентина манит негра”, “Ценит негра аргентинец”, “Леша на палке клапана шел”. «А роза упала на лапу Азора». Такие слова называются палиндромами.

Ими увлекались многие поэты.

3. СИММЕТРИЯ В БИОЛОГИИ.

На явления симметрии в живой природе обратили внимание ещё в Древней Греции пифагорейцы в связи с развитием учения о гармонии (V век до н.э.). В XIX веке появились единичные работы, посвящённые симметрии в растительном и животном мире.

В XX веке усилиями российских учёных - В Беклемишева, В Вернадского, В Алпатова, Г.Гаузе - было создано новое направление в учении о симметрии - биосимметрика, которое, исследуя симметрии биоструктур на молекулярном и надмолекулярном уровнях, позволяет заранее определить возможные варианты симметрии в биообъектах, строго описывать внешнюю форму и внутреннее строение любых организмов.

Характерная для растений симметрия конуса хорошо видна на примере любого дерева.

Дерево поглощает из почвы влагу и питательные вещества за счёт корневой системы, то есть внизу, а остальные жизненно важные функции выполняются кроной, то есть наверху. Поэтому направления "вверх" и "вниз" для дерева, существенно различны. А направления в плоскости, перпендикулярной к вертикали, для дерева фактически неразличимы: по всем этим направлениям к дереву в равной мере поступают воздух, свет, и влага. В результате появляется вертикальная поворотная ось и вертикальная плоскость симметрии. У цветковых растений в большинстве проявляется радиальная и билатеральная симметрия. Цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей. Цветки, имея парные части, считаются цветками с двойной симметрией и т.д. Тройная симметрия обычна для однодольных растений, пятерная - для двудольных

Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии.

Сферическая симметрия имеет место у радиолярий и солнечников, тела которых сферической формы, а части распределены вокруг центра сферы и отходят от неё. У таких организмов нет ни передней, ни задней, ни боковых частей тела, любая плоскость, проведённая через центр, делит животное на одинаковые половинки.

При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Это кишечнополостные, иглокожие, морские звёзды.

Человеческое тело обладает билатеральной симметрией (внешний облик и строение скелета). Эта симметрия всегда являлась и является основным источником нашего эстетического восхищения хорошо сложенным человеческим телом. Тело человека построено по принципу двусторонней симметрии.

Большинство из нас рассматривает мозг как единую структуру, в действительности он разделён на две половины. Эти две части - два полушария - плотно прилегают друг к другу. В полном соответствии с общей симметрией тела человека каждое полушарие представляет собой почти точное зеркальное отображение другого. Управление основными движениями тела человека и его сенсорными функциями равномерно распределено между двумя полушариями мозга. Левое полушарие контролирует правую сторону мозга, а правое - левую сторону.

Физическая симметрия тела и мозга не означает, что правая сторона и левая равноценны во всех отношениях. Достаточно обратить внимание на действия наших рук, чтобы увидеть начальные признаки функциональной симметрии. Лишь немногие люди одинаково владеют обеими руками; большинство же имеет ведущую руку.

4. СИММЕТРИЯ В ИССКУСТВЕ

В геометрических орнаментах всех веков запечатлены неиссякаемые фантазия и изобразительность художников и мастеров, чьё творчество было ограничено жёсткими рамками, установленными неукоснительным следованием принципам симметрии. Трактуемые несравненно шире идеи симметрии нередко можно встретить в живописи, скульптуре, музыке и поэзии. Во многих случаях именно язык симметрии оказывается особенно пригодным для обсуждения произведений искусства, даже если последние отличаются отклонениями от симметрии или их создатели стремились умышленно её избежать.

СИММЕТРИЯ В ЖИВОПИСИ

Картина – это отнюдь не цветная фотография. Взаимное расположение фигур, сочетание поз и жестов, выражения лиц, чередование цвета, комбинация тонов – все это тщательно обдумывается художником, заботящемся об определенном эмоциональном воздействии картины на зрителя. Используя асимметричные элементы, художник должен создать нечто, обладающее в целом скрытой симметрией. О своей работе над картинами В.И. Суриков писал так: «А какое время надо, чтобы картина утряслась так, чтобы переменить ничего нельзя было. Действительные размеры каждого предмета найти нужно. Важно найти замок, чтобы все части соединить. Это - математика».

Для анализа симметрии изображения можно обратиться к хранящейся в Эрмитаже картине гениального итальянского художника и ученого Леонардо да Винчи «Мадонна Литта». Можно обратить внимание: фигуры мадонны и ребенка вписываются в правильный треугольник, который вследствие своей симметричности особенно ясно воспринимается глазом зрителя. Благодаря этому мать и ребенок сразу же оказываются в центре внимания, как бы выдвигаются на передний план. Голова мадонны совершенно точно, но в то же время естественно помещается между двумя симметричными окнами на заднем плане картины. В окнах просматриваются спокойные горизонтальные линии пологих холмов и облаков. Все это создает ощущение покоя и умиротворенности, усиливаемое за счет гармоничного сочетания голубого цвета с желтоватыми и красноватыми тонами. Внутренняя симметрия картины хорошо ощущается. А что можно сказать об асимметрии? Асимметрия хорошо проявляется, например, в тельце ребенка, которое неправильно разрезает упомянутый выше треугольник. И, кроме того, есть одна в высшей степени выразительная деталь. Благодаря взаимной замкнутости, завершенности линий фигуры мадонны создается впечатление полного безразличия мадонны к окружающему миру, и в частности к зрителю. Мадонна вся сосредоточена на младенце; она нежно держит его, нежно глядит на него. Все ее мысли сосредоточены только на нем. И вдруг вся эта замкнутость картины в себе исчезает, как только мы встречаемся со взглядом ребенка. Именно здесь внутренняя уравновешенность композиции нарушается: спокойный и внимательный взгляд обращен прямо на зрителя, через него картина раскрывается во внешний мир.Получается, что всякий раз, когда мы, восхищаемся тем или иным произведением искусства, говорим о гармонии, красоте, эмоциональности воздействия, мы тем самым касаемся одной и той же неисчерпаемой проблемы – проблемы соотношения между симметрией и асимметрией. Как правило, находясь в музее или в концертном зале, мы не задумываемся над этой проблемой. Ведь нельзя одновременно и ощущать, и анализировать ощущение. Пример с картиной Леонардо да Винчи убеждает в том, что анализ симметрии – асимметрии все же очень полезен: картина начинает восприниматься острее.

СИММЕТРИЯ В АРХИТЕКТУРЕ

Внимательно посмотрите вокруг и вы убедитесь в том, что симметрия встречается в архитектуре, быту, в мире растений, животных. Примерами фигур, обладающих центральной симметрией, является окружность, параллелограмм, прямая, отрезок и т.д. Треугольник не имеет центра симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля. С симметрией часто встречаемся в искусстве, архитектуре , технике .

Самое непосредственное отношение к симметрии имеет композиция. Великий немецкий поэт Иоганн Вольфганг Гете утверждал, что «всякая композиция основана на скрытой симметрии». Владеть законами композиции – это значит владеть законами симметрии. Три основных закона композиции предполагают трансляционно-тождественное повторение элементов структуры, контрастное повторение, варьированное повторение. Это выглядит как орнамент во времени.

Нас всегда будут восхищать «орнаменты», созданные великим русским поэтом А.С. Пушкиным. Вот относительно простой, изящный пушкинский «орнамент»:

…В гранит оделася Нева;

Мосты повисли над водами;

Темнозелеными садами

Ее покрылись острова…

Пушкин А.С. «Медный всадник»

ЗАКЛЮЧЕНИЕ

С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого развития. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность. Симметрия буквально пронизывает весь окружающий нас мир

Знание геометрических законов природы имеют огромное практическое значение. Мы должны не только научиться понимать эти законы, но и заставлять служить нам на пользу.

О, симметрия! Гимн тебе пою!

Тебя повсюду в мире узнаю

Ты в Эйфелевой башне, в малой мошке,

Ты в елочке, что у лесной дорожки.

С тобою в дружбе и тюльпан и роза

И снежный рай – творение мороза.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Атанасян Л.С. Бутузов В.Ф. и др. Геометрия 7-9 : учебник для общеобразовательных учреждений, М., Просвещение, 2007

2. Балк М.Б., Балк Г.Д. Математика после уроков – М.: Просвещение, 1971

3. Вейл Г. Симметрия. M., Наука, 1968.

4. Вульф Г.В. Симметрия и ее проявления в природе. М., Изд. Отд. Нар. ком. Просвещение, 1991.

5. Тарасов Л. Этот удивительный симметричный мир. М., 1982 г.

6. Шубников А.В., Копцик В.А. Симметрия в науке и искусстве. М., 1976.

Конец формы