Конспект урока «Решение квадратных уравнений» по математике для 8 класса
| ФИО Севрюкова Валентина Петровна |
| Место работы МБОУ Кагальницкая СОШ №1ст.Кагальницкая Ростовская область |
| Должность учитель |
| Предмет математика |
| Класс 8 |
| Тема урока Решение квадратных уравнений |
| |
ПЛАН-КОНСПЕКТ УРОКА по алгебре 8 класс
«Решение квадратных уравнений»
Цели урока:
Образовательная: обобщение и систематизация знаний учащихся, закрепление и совершенствование навыков решения квадратных уравнений.
Развивающая: помочь самореализоваться ребёнку на уроке.
Воспитательная: самосовершенствование личностных качеств ученика и развитие его способности принимать решение.
Тип урока: урок обобщающего повторения
Формы работы учащихся: групповая, индивидуальная
Необходимое техническое оборудование: компьютер, проектор, экран.
Структура урока:
-
Организационно-мотивационный момент.
-
Целеполагание.
-
Теоретическая разминка.
-
Закрепление умений и навыков по изучаемой теме:
-
Работа в группах
-
Историческая справка
-
Самостоятельная работа
-
Подведение итогов, рефлексия.
Домашнее задание.
Ход урока.
-
Организационно-мотивационный момент.
Математику не зря называют «царицей наук». Ей больше, чем какой–нибудь другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики – любознательность. Постараемся доказать это на уроке. А прежде, чем начать доказывать это, давайте улыбнемся друг другу. Ведь с улыбки начинается все, все, все.
-
Целеполагание.
Рассмотрите уравнения, записанные на доске, и выберете те уравнения, которые нужно исключить из данной группы и объясните почему.(слайд №1,2)
А, как вы думаете, какая тема сегодняшнего урока? Что будет сегодня на уроке в роли «главного героя»? ( «Решение квадратных уравнений») Правильно.(слайд №3)
Цель нашего урока:
научиться
-
распознавать квадратные уравнения;
-
решать квадратные уравнения различных видов, а также уравнения, сводящиеся к ним;
-
определять наличие корней квадратных уравнений по дискриминанту и коэффициентам.
«Уравнение – это золотой ключ,
открывающий все математические сезамы.»
С. Коваль
Квадратные уравнения встречаются не только на уроках алгебры, но и на геометрии, физике. Эти уравнения занимают одно из главных мест в математике и будут использоваться при изучении различных тем в старших классах.(слайд №4 )
III. Теоретическая разминка.
1. А что же такое квадратное уравнение? Дайте определение квадратного уравнения.( Квадратным уравнением называют уравнение вида ax2+bx+c=0, где коэффициенты a,b,c – любые действительные числа, причем a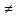 0)( слайд №5 )
0)( слайд №5 )
А сейчас я предлагаю вам следующее задание.
2. Составьте квадратное уравнение с заданными коэффициентами a, b и c.Заполните таблицу.( слайд №6)
| a | b | c | Уравнения | |
| 1 | -3 | 5 | 0 | |
| 2 | 4 | 0 | 16 | |
| 3 | 2 | 7 | -8 | |
| 4 | 1 | -5 | 6 | |
| 5 | 1 | -4 | 0 | |
(Учащиеся выходят к доске и записывают полученные уравнения)
3.На какие группы можно разбить полученные уравнения? (Полные – 3,4 и неполные уравнения – 1,2,5).
4.Какие уравнения называются полными? Неполными? ( Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого b и c отличны от нуля.( слайд №7) Неполное квадратное уравнение – это уравнение, у которого присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b,c равен нулю). (слайд №8)
5.На какие еще группы можно разбить данные уравнения? (Приведенные – 4,5 и неприведённые – 1,2,3)
6.Какие уравнения называются приведёнными? Неприведёнными? (Квадратное уравнение называют приведенным, если его старший коэффициент равен 1; квадратное уравнение называют неприведенным, если его старший коэффициент отличен от 1).( слайд №9)
IV. Закрепление умений и навыков по изучаемой теме:
-
Работа в группах
Молодцы, ребята! А сейчас переходим к работе в группах.
1.Каждая группа получает карточку с заданием: решить квадратные уравнения и сделать вывод о корнях данного вида квадратных уравнений.
1 группа
а)3x2=0, б) -7x2=0, в) 1,3x2=0.
Неполное квадратное уравнение вида ax2=0. Вывод: уравнение имеет 1 корень x=0.
2 группа
а) 4x2+36x=0; б) x2-3x=0; в) 2x2 +10x=0.
Неполное квадратное уравнение вида ax2+bx=0. Вывод: уравнение имеет 2 корня x1=0, x2= - 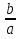
3 группа
а) x2- 9=0; б) x2+ 64=0; в) 3x2-12=0.
Неполное квадратное уравнение вида ax2+c=0. Вывод: уравнение не имеет корней при c 0, и 2 корня x1,=
0, и 2 корня x1,=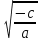 и x2=-
и x2=- 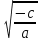 если c
если c 0.
0.
2. Каждая группа получает карточку с заданием решить полные квадратные уравнения и сделать вывод.
1 группа
а)x2- 6x +9=0, б) -25x2+10x-1=0, в) 16x2+8x+1=0.
Вывод: если D=0, то уравнение имеет 1 корень x=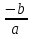
2 группа
а) 7x2+x+1=0; б) -2x2-3x-5=0; в) 2x2 -3x+2=0.
Вывод: если D 0, то уравнение не имеет действительных корней.
0, то уравнение не имеет действительных корней.
3 группа
а) 7x2-4x-3=0; б) -5x2+8x-3=0; в) 9x2 -13x+4=0.
Вывод: если D 0, то уравнение имеет 2 корня x1=
0, то уравнение имеет 2 корня x1=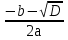 и x2=
и x2=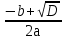
-
Историческая справка..
Молодцы, ребята! Кстати, а вы знаете, когда появились первые квадратные уравнения?( слайд №10,11)
Очень давно. Их решали в Вавилоне около 2000 лет до нашей эры, а Европа в 2002 г. отпраздновала 800летие квадратных уравнений, потому что именно в 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения. И лишь в 17 веке, благодаря Ньютону, Декарту и другим ученым эти формулы приняли современный вид. А вот понятие дискриминант придумал английский ученый Сильвестр, он называл себя даже “математическим Адамом” за множество придуманных терминов. В древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто представлялись в стихотворной форме.
-
Самостоятельная работа.
Хорошо. В группах мы поработали. Теперь посмотрим, как вы умеете работать самостоятельно. Вам предлагается трехуровневая работа. На парте у каждого лежат карточки с заданиями разного цвета. Если вы еще не уверены в своих силах и желаете закрепить решение уравнение, то выбираете уровень А (синий цвет). Если считаете, что материал усвоен хорошо – В (зелёный цвет). Ну, а если желаете испробовать свои силы на более сложных заданиях – уровень С (розовый цвет) для вас. На выполнение самостоятельной работы 10 минут.
V. Подведение итогов, рефлексия.
Оценки за самостоятельную работу вы узнаете на следующий урок. Оценки за работу на уроке получают…
А сейчас ребята скажите, мы достигли целей, которые ставили в начале урока?
Цель нашего урока:
научиться
-
распознавать квадратные уравнения;
-
решать квадратные уравнения различных видов, а также уравнения, сводящиеся к ним;
-
определять наличие корней квадратных уравнений по дискриминанту и коэффициентам.
А теперь оцените свою работу на уроке. На столах кружочки красного, желтого и зеленого цветов. Ваша задача поднять тот кружочек, который соответствует вашему ответу на мои вопросы.
- Могу решать уравнения самостоятельно (зеленый кружочек)
- Нужна помощь (желтый кружочек)
- Совсем не могу решать уравнения (красный кружочек).( слайд №12)
VI. Домашнее задание.
№26.24(а,б), №26.26(а)*
Здесь представлен конспект к уроку на тему «Решение квадратных уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

