Конспект урока «Решение тригонометрических уравнений» по математике
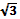
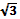
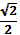
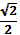
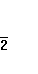
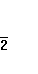
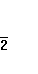
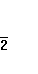
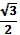
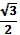
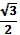
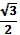
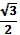
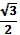
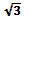
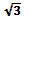
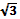
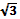






ПЛАН – КОНСПЕКТ
ОТКРЫТОГО УРОКА
НА ТЕМУ
«Решение тригонометрических уравнений»
Преподаватель:
Л.П. Бабенко
2013 г.
Дата 19.02.2013 г.
Группа ММО 9-1
Предмет – математика
Тема урока: Решение тригонометрических уравнений
Цели:
- дидактическая – расширить объём знаний по разделу «Уравнения» через решение тригонометрических уравнений;
- развивающая – развитие познавательной активности обучающихся, умения обобщать, анализировать, сравнивать;
- воспитательная – воспитание внимания, добросовестного отношения к учебе.
Девиз урока: научился сам – научи другого, обучал другого – учился сам.
Тип технологии – традиционная
Тип урока – комбинированный урок
Методы обучения – словесный, наглядный, аудиовизуальный , упражнения.
Форма организации познавательной деятельности – фронтальная индивидуальная
Формы контроля и самоконтроля – устная, письменная, групповая
Межпредметные связи – физика, химия, электротехника
КМО: плакат «Тригонометрические функции, портреты ученых Архимеда, Евклида, раздаточный материал, решебник, таблицы, задачник Мордкович
Продолжительность урока – 45 минут
Уровень обучающихся 15 – 16 лет
Ход урока
I Организационный момент
– проверка наличия необходимого для урока (тетради, ручка¸ раздаточный материал)
- перекличка группы: по списку, присутствуют, отсутствуют (причина)
II Мотивация учебной деятельности, целевая установка на урок
- сообщение целей урока: расширить объём знаний по разделу «Уравнения»
- задачи: продолжить отработку навыков решения тригонометрических уравнений.
III Проверка домашнего задания
Проверяем домашнее задание и отвечаем на появившиеся вопросы.
IV Актуализация опорных знаний.
Устная работа с заданиями на доске:
- какие тригонометрические функции являются периодическими (назвать функцию и ее период)
- дописать выражения tg x = ctg x =
При переносе членов уравнения из одной части в другую, они . . . (сменяют знаки на противоположные)
- какому уравнению соответствует формула, дописать ее
y = ± arc. . . + 2 πn, n Є (cos x = a)
y = (-1)n arc . . . + πn, n Є (sin x = a)
y = arc . . . + πn, n Є (tg x = a)
- Могут ли функции y = sin x и y = cos x одновременно быть равны 0? Нет
- Какие меры измерения углов вы знаете? (градусы, радианы, румбы - метрическая мера), обороты, тысячная (в артиллерии), грады, сантиграды ?
- преподаватель рассказывает об ученых, занимавшихся вопросами тригонометрии (Птолемей) и в каких областях она применяется.
Работа по карточкам, согласно инструкции:
- каждый в паре решает пример из карточки. Первый партнер объясняет решение своего примера второму партнеру и записывает решение в тетради партнера, рассказывая решение вслух. Затем эту же операцию проделывает второй партнер. Примеры 3 и4 решают совместно в тетрадях, затем получают новую карточку (при этом помечая номер карточки). И так, пока не решат примеры из всех карточках.
Раздаю карточки 4 экземпляра.
Сообщаю задание для «свободной минутки»
x2 = 3x – 1 4x2 – 2x = 0 8x2 – x – 5 = 0
ctg x = 3 cos 2x = 5
Ответы – 1) ; 2) 0;3) ; 4) arcctg 5 + πn; 5) ɸ
V Валеологическая пауза.
Показываю упражнения на расслабление тела.
VI Изучение нового материала и его закрепление.
Сообщаю о заданиях на «свободной минутке» - № 349, 360, Мордкович.
2 cos x + = 0
2 cos x = -
cos x = -
x = ± arcos ( - ) + 2 πn
Обучаемые решают и проверяют ответы по решебнику. Задачи № 349, 360.
Пояснение к № 360 а, б, в (на чем основано решение, обращаюсь к устному счету)
VII. Подведение итогов. Сообщаю оценки по результатам работы.
VIII. Рефлексивно-оценочный этап. Обучаемые оценивают урок.
IX. Домашнее задание. Мордкович, задание № 350, 360 г.
Принцип работы с карточками (4 варианта по 4 примера на решение простейших тригонометрических уравнений):
Каждая пара должна проработать со всеми вариантами. Когда обоими студентами решение выполнено, они меняются заданиями и проверяют друг друга. Карточки пары передают по мере выполнения. Если задание выполнено быстро, есть задание «Свободная минутка».
Структура урока
| Содержание урока | Время | Деятельность преподавателя | Деятельность обучаемых | КМО | |
| 1 | Организационный момент | 2 мин | Проверяет наличие обучающихся, а так же всё необходимое для учебного процесса | Каждый проверяет наличие необходимого на уроке (ручки, линейки, карандаши, учебники) | Раздаточный материал, учебники, линейки, карандаши, ручки |
| 2 | Мотивация учебной деятельности, целевая установка на урок | 1 мин | Ставит цели и задачи урока | Восприятие, запоминание информации | Оформление доски |
| 3 | Проверка домашнего задания | 2 мин | Проверяет домашнее задание | Проверяют правильность выполненного задания | а) задания для устного счёта |
| 4 | Актуализация опорных знаний | 15 мин | а) проводит устную работу; б) рассказывает об областях применения тригонометрии; в) предлагает работу в парах, сообщает инструкцию для работы с раздаточным материалом; г) сообщает задание для «свободной минутки» | а) устно отвечают на вопросы преподавателя; б) рассказывают о том, как связаны физика и химия с понятием «тригонометрическое уравнение»; в) работа по карточкам по инструкции; г) воспринимают и запоминают информацию | |
| 5 | Валеологическая пауза | 2 мин | Показывает упражнения | Повторение упражнений | |
| 6 | Изучение нового материала и его закрепление | 16 мин | а) поясняет ход работы у доски; б) поясняет задания к «свободной минутке» | Вызываются отдельные обучающиеся к доске. Они решают и проверяют работу по решебнику. | Проверяют правильность выполнения задания по решебнику |
| 7 | Подведение итогов | 2 мин | Преподаватель выставляет оценки | | |
| 8 | Рефлексивно-оценочный этап | 3 мин | Предлагает ответить на вопрос «Ладошки» | Отвечают на вопросы | |
| 9 | Домашнее задание | 2 мин | Комментирует дачу домашнего задания | | |
ОФОРМЛЕНИЕ ДОСКИ К 19.02.2013
Число 19.02.2013 г.
| Тема урока: Решение тригонометрических уравнений Девиз урока: Научился сам – научи другого, обучал другого – учился сам. № 349, 360 | Задания для устного счёта: 1. Какие тригонометрические функции являются периодическими и назвать их периоды (показать на графике) 2. Дописать выражения tg x = ctg x = 3. Какие меры измерения углов вы знаете? (градусы, радианы, румбы - метрическая мера), обороты, тысячная (в артиллерии), грады - ? , сантиграды - ? 4. Могут ли функции y = sin x и y = cos x одновременно быть равны 0 ? 5. Дописать формулы, для каких уравнений они предназначены? y = ± arc. . . + 2 πn, n Є y = (-1)n arc . . . + πn, n Є y = arc . . . + πn, n Є 6. приведите пример простейшего тригонометрического уравнения. 7. Каким условиям должно отвечать число а в уравнении sin x = a, cos x = a ( -1 ≤ a ≥ 1) |
Решебник
№ 349
а) x = ± arcos ( - ) + 2 πn
б) x = (-1)n arcsin (- ) + πn
в) x = ± arccos + 2 πn
г) х = (-1)n arcsin ( - ) + πn
__________________________________________________________
№ 360
а) x = arc tg (- ) + πn
б) x =arc tg (-1) + πn
в) x = arc tg 3 + πn
Здесь представлен конспект к уроку на тему «Решение тригонометрических уравнений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

