Конспект урока «Использование формул арифметической прогрессии при решении прикладных задач» по алгебре для 9 класса

Урок по алгебре.

9 класс

Тема: Использование формул арифметической прогрессии при решении прикладных задач.

Цель: обобщить знания по теме «Арифметическая прогрессия»,

Задачи: 1. Сформировать умение решать задачи прикладного характера по данной теме.

2. Развивать логическое мышление и умение анализировать условия (приводить условие к известным обозначениям и формулам).

Ход урока:

1. Организационный момент.

2. Актуализация опорных знаний:

Устные вопросы:

1. Что такое последовательность.

2. Какие виды последовательности вы знаете?

3. Какая последовательность называется арифметической прогрессии?

Устные упражнения:

1. Будет ли последовательность арифметической прогрессией? Почему?

(a_n): 2; 9; 16; 23…

(b_n): ; ; …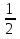

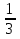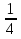(c_n): а ; а; а..

2. Пусть (а_n) : 1 ; 3 ; 5…- арифметическая прогрессия.

Найти : а₁, а₄ ; а₇; а₁₁.

3. Найти S_n , если а₁=2 ; а₅=6; n=5 ,

а₁=0 ; d=6 ; n=4?

a₁=-2; а₃=6 ; n=3.

4. Математический диктант (обобщение знаний и умений)

1. Запишите формулу n-члена арифметической прогрессии.

2. Запишите формулу суммы n первых членов арифметической прогрессии.

3. Сколько членов вмещает конечная арифметическая прогрессия: 3, 6, 9,…273.

4. Запишите формулу n-го члена арифметической прогрессии: 3, 6, 9,…273.

5. Найти сумму чисел 3+6+9+….+273, если все слагаемые являются членами арифметической прогрессии.

6. Запишите формулу для нахождения суммы n первых членов арифметической прогрессии: 3, 6, 9,…273.

3. Формирование умений решения задач прикладного смысла.

1. Обобщение темы по схеме.

4. Решение задач.

2. Вводная беседа.

Прикладные задачи - это задачи физического, геометрического, химического смысла, которые решаются с помощью алгебраических формул.

Цель нашего урока: рассмотреть прикладные задачи, которые можно решить, используя определение, формулы, свойства арифметической прогрессии.

Мы рассмотрим задачи геометрического и физического характера.

Задача №1.

Свободно падающее тело проходит за первую секунду 4,9м, а за каждую последующую на 9,8м больше, чем за предыдущую. Какое расстояние оно пройдет за 21-ую секунду, за 21 секунду.

Решение:

Запишем расстояние, которое пройдет тело за несколько секунд:

(a_n): 4,9м; 14,7м; 24,5м…

Мы получили арифметическую прогрессию (a_n), в которой

a₁=4,9м, d=9,8м

Чтоб найти, какое расстояние пройдет тело за 21-ую секунду, надо вычислить a₂₁/

a₂₁=a₁+20d=4,9+20•9,8=200,8 (м)

Чтоб найти какое расстояние пройдет тело за 21 секунду, надо найти сумму всех расстояний за это время, т.е. S₂₁

S₂₁=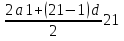==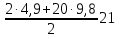2159,85 (м).

Ответ: 200,8м, 2159,85м.

Таким образом, чтоб решить прикладную задачу надо:

1. Ввести арифметическую прогрессию.

2. Переформулировать условие на определение, формулы арифметической прогрессии.

Задача №2.

В многоугольнике один угол равен 100⁰, каждый последующий больше предыдущего на 10⁰. Какой это многоугольник?

Решение:

Составим арифметическую прогрессию градусных мер углов данного многоугольника:

(α_n): α₁=100⁰, α₂=110⁰, α₃=120⁰…

Данная последовательность – арифметическая прогрессия, в которой

α₁=100⁰, d=10⁰.

Пусть многоугольник имеет n сторон, тогда прогрессия имеет n членов. Сумму внутренних углов многоугольника можно найти по формуле 180 (n-2) или по формуле суммы арифметической прогрессии S_n=.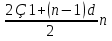

Подставим данные, получим уравнение:

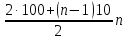=180(n-2)

(100+5n-5)n=180(n-2)

95n+5n²-180n+360=0

5n²-85n+360=0

n²-17n+72=0

По теореме Виета n₁=8, n₂=9

Ответ: 8 или 9.

Задача №3.

Два тела движутся на встречу друг другу. Первое движется со скоростью 10 м/с, второе за первую секунду проходит 3м, за каждую последующую на 5м больше. Если первоначальное расстояние между ними 153м, найдите через сколько секунд тела встретятся.

Решение:

10м/с_______________________________________3м/с, 8м/с, 11м/с….

153м

Расстояние за каждую секунду второго тела составляет арифметическую прогрессию.

Пусть встреча произойдет через n секунд, тогда первое тело пройдет 10n м, а расстояние второго – это сумма арифметической прогрессии, в которой а₁=3м, d=5м.

Вычислим S_n=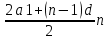, тогда Sn=0,5n+2,5n² (м)

По условию расстояние равно 153м.

Составляем уравнение:

0,5n+2,5n²+10n=153

n²+4,2n-61,2=0

D=b²-4ac=17,64+244,8=262,44

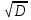=16,2

n_1,2=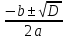, n₁=6, n₂=10,2.

Т.к. n- количество членов арифметической прогрессии, то n€N, поэтому n=6.

Ответ: 6с.

5. Итог урока.

6. Домашнее задание: придумать условие и решить две задачи прикладного характера.