Конспект урока «Арифметическая и геометрическая прогрессии» по алгебре для 9 класса
Ф.И.О автора материала: Дыда Татьяна Ивановна
Место работы: МАОУ СОШ № 18, г. Армавир, Краснодарский край
Должность: Учитель математики
Обобщающее повторение в системе
подготовки к ГИА по математике
по теме:
«Арифметическая и геометрическая прогрессии».

Автор – составитель:
Дыда Т. И. – учитель математики
МАОУ СОШ № 18 г. Армавир
§ 1. Числовая последовательность.
Справочный материал.
-
Если каждому натуральному числу n отнесено по некоторому закону число x, то говорят, что задана числовая последовательность:
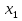 ,
, 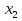 ,
, 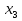 , …,
, …,  .
.
Числа 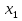 ,
, 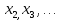 называются членами последовательности, они не обязательно различны между собой. В некоторых случаях последовательность задаётся формулой её общего члена
называются членами последовательности, они не обязательно различны между собой. В некоторых случаях последовательность задаётся формулой её общего члена  = f (n), n
= f (n), n 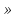 N. Зная её, мы можем получить любой член последовательности. Для этого достаточно в правую часть формулы вместо n подставить номер искомого члена.
N. Зная её, мы можем получить любой член последовательности. Для этого достаточно в правую часть формулы вместо n подставить номер искомого члена.
Например:  =
= 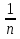 : 1,
: 1, 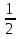 ,
, 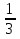 , …,
, …, 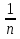 , … ;
, … ;
 =
=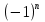 : 1; -1; 1; -1; …; 1; … ;
: 1; -1; 1; -1; …; 1; … ;
 = 5 : 5; 5; 5; …; 5; … .
= 5 : 5; 5; 5; …; 5; … .
-
Последовательность называется возрастающей, если для всех n,

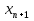 .
.
Последовательность называется убывающей, если для всех n,  >
> 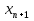 .
.
Возрастающие и убывающие последовательности называются монотонными.
Например, последовательности монотонные: 1, 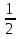 ,
, 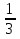 , …,
, …, 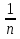 , … ;
, … ;
1, 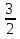 ,
, 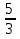 , …,
, …, 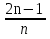 , …;
, …;
1, 4, 9, …, n², … .
Последовательности не монотонные: 1, - 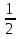 ,
, 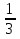 , …,
, …, 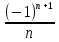 ,…;
,…;
1, 0, 3, 0,…, 2n – 1, 0, … .
Замечание. К монотонным последовательностям относятся также неубывающие ( ≤
≤ 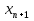 ) и невозрастающие последовательности (
) и невозрастающие последовательности ( ≥
≥ 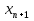 ).
).
Упражнения.
-
а) Последовательность (
 ) задана формулой
) задана формулой  =
= 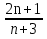 .
.
Найдите 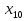 ,
, 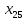 ,
, 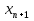 ,
, 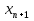 -
- 
б) Последовательность (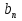 ) задана формулой
) задана формулой 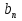 =
= 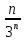 .
.
Найдите 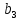 ,
, 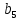 ,
, 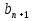 ,
, 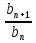 .
.
2. Выпишите первые пять членов последовательности ( ) и задайте эту последовательность формулой n-го члена, если
) и задайте эту последовательность формулой n-го члена, если 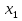 = -10,
= -10, 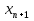 =
=  + 5, n ≥ 1.
+ 5, n ≥ 1.
3. Для каких членов последовательности (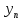 ) выполняется условие:
) выполняется условие:
а) 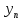 > 200, если
> 200, если 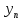 = 2n – 5; б)
= 2n – 5; б) 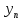 ≤ 30, если
≤ 30, если 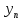 = 3n – 100?
= 3n – 100?
4. Составьте одну из возможных формул n - го члена последовательности:
а) 1, 4, 9, 16, 25, … ; в) 0, 3, 8, 15, …; д) 2, 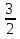 ,
, 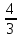 ,
,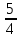 ,… ;
,… ;
б) 2, -2, 2, -2, … ; г) 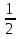 ,
, 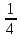 ,
, 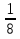 ,
, 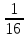 ,… ; е) 5, 0, 5, 0, 5, ….
,… ; е) 5, 0, 5, 0, 5, ….
5. Изобразите последовательность (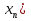 точками координатной прямой:
точками координатной прямой:
а)  =
= 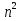 + 1; в)
+ 1; в)  =
= 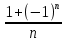 ;
;
б)  = 1 -
= 1 - 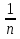 ; г)
; г)  =
= 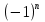 ·
· 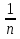 .
.
6. Последовательность (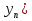 задана формулой
задана формулой 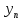 = - 3 ·
= - 3 · 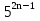 . Принадлежит ли этой последовательности число: ― 1875?
. Принадлежит ли этой последовательности число: ― 1875?
7. Дана последовательность общий член которой выражается формулой:
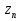 = (4n + 5) (n + 1). Докажите, что последовательность убывающая.
= (4n + 5) (n + 1). Докажите, что последовательность убывающая.
8. Является убывающей или возрастающей последовательность 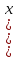 ),
),
если  =
= 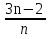 ?
?
9. Последовательность задана формулой  = 2n –
= 2n – 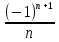 . Какое из следующих чисел является членом этой последовательности?
. Какое из следующих чисел является членом этой последовательности?
1) 2; 2) 4 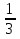 ; 3) 8
; 3) 8 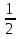 ; 4) 5
; 4) 5 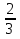 .
.
10. Последовательность задана формулой n-го члена. У какой из них следующий член больше предыдущего?
1)  =
= 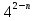 ; 2)
; 2) =
= 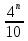 ; 3)
; 3)  =
= 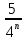 ; 4)
; 4)  = 2 ·
= 2 · 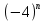 .
.
11. Последовательность задана формулой 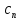 =
= 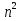 + 1. Какое из чисел является членом этой последовательности?
+ 1. Какое из чисел является членом этой последовательности?
1) 4 ; 2) 6 ; 3) 5 ; 4) 3 .
12. Последовательность задана формулой 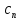 =
= 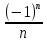 . Какое из этих чисел не является членом этой последовательности?
. Какое из этих чисел не является членом этой последовательности?
1) 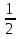 ; 2)
; 2) 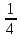 ; 3)
; 3) 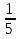 ; 4)
; 4) 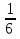 .
.
13. В двух последовательностях, n-е члены которых выражаются формулами  = n(n + 36) +7 и
= n(n + 36) +7 и 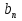 = n(5n + 9), найдите равные члены с одним и тем же номером.
= n(5n + 9), найдите равные члены с одним и тем же номером.
14. Дана последовательность ( ), где n
), где n  N. Выпишите 4-6 членов этой последовательности, изобразите их точками на координатной прямой и ответьте на вопросы: является ли эта последовательность возрастающей или убывающей, существует ли число, к которому члены последовательности неограниченно приближаются?
N. Выпишите 4-6 членов этой последовательности, изобразите их точками на координатной прямой и ответьте на вопросы: является ли эта последовательность возрастающей или убывающей, существует ли число, к которому члены последовательности неограниченно приближаются?
1)  = -2n; 4)
= -2n; 4)  = 5n; 7)
= 5n; 7)  =
= 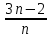 ;
;
2)  =
= 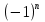 · n; 5)
· n; 5)  =
=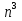 ; 8)
; 8)  = 4 +
= 4 + 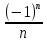 ;
;
3)  =
= 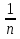 ; 6)
; 6)  =
= 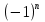 +
+ 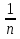 ; 9)
; 9)  = -2
= -2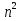 + 3.
+ 3.
15. В последовательность  =
= 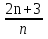 найдите расстояние от точки 2 до точки:
найдите расстояние от точки 2 до точки: 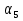 ;
; 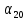 ;
; 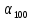 .
.
§ 2. Арифметическая прогрессия.
Справочный материал.
-
Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же число, называется арифметической прогрессией.
Обозначается - ( ):
):  ,
,  ,
, 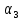 , …,
, …,  , … .
, … .
-
Разность между любым членом прогрессии и ему предшествующим равна одному и тому же числу, то есть
 -
-  =
= 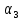 -
-  = … =
= … = 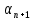 -
-  = … . Это число называют разностью арифметической прогрессии и обозначают
= … . Это число называют разностью арифметической прогрессии и обозначают
буквой d.
-
Для того чтобы задать арифметическую прогрессию (
 ), достаточно знать её первый член
), достаточно знать её первый член  и разность d.
и разность d. -
Приведём примеры арифметических прогрессий:
-1; 5; 11; 17; 23; 29; …; здесь  = -1, d = 5 – (-1) =11 - 5 = 17 – 11 = 6;
= -1, d = 5 – (-1) =11 - 5 = 17 – 11 = 6;
17; 14; 11; 8; 5; 2; -1; - 4; …; здесь  = 17, d = 14 – 17 = 11 – 14 = -3;
= 17, d = 14 – 17 = 11 – 14 = -3;
8; 8; 8; 8; 8; 8; …; здесь  = 8, d = 8 – 8 = 0.
= 8, d = 8 – 8 = 0.
-
Если d > 0, то прогрессия возрастающая;
если d , то прогрессия убывающая;
если d = 0, то прогрессия постоянная последовательность.
-
Последовательность (
 ) является арифметической прогрессией тогда и только тогда, когда её любой член, начиная со второго, является средним арифметическим предшествующего и последующего членов,
) является арифметической прогрессией тогда и только тогда, когда её любой член, начиная со второго, является средним арифметическим предшествующего и последующего членов,
то есть: 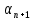 =
= 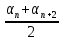 , где n
, где n 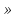 N.
N.
-
Формулы n-го члена арифметической прогрессии имеют вид:
 =
= 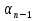 + d и
+ d и  =
=  + d(n – 1) - основные формулы.
+ d(n – 1) - основные формулы.
-
Формулы суммы n первых членов арифметической прогрессии имеют вид:
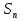 =
= 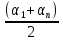 · n и
· n и 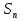 =
= 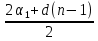 · n
· n
-
Сумма членов, равноудалённых от концов прогрессии, есть величина постоянная, то есть
 +
+  =
=  +
+ 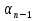 = … .
= … .
Упражнения с решениями.
Задача 1. Найти пятнадцатый член арифметической прогрессии
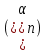 : 3; 7; 11; … .
: 3; 7; 11; … .
Решение.
В прогрессии ( ):
):  = 3,
= 3,  = 7,
= 7, 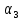 = 11, n = 15.
= 11, n = 15.
Разность арифметической прогрессии d =  -
-  ; d = 7 - 3 = 4.
; d = 7 - 3 = 4.
По формуле  =
=  + d(n – 1),
+ d(n – 1), 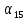 =
=  + 14d = 3 + 4 · 14 = 59.
+ 14d = 3 + 4 · 14 = 59.
Ответ: 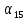 = 59.
= 59.
Задача 2. В арифметической прогрессии ( ) известно, что
) известно, что  = 3, d = 4. Найдите
= 3, d = 4. Найдите 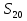 .
.
Решение.
По формуле 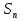 =
= 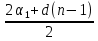 · n , имеем
· n , имеем 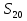 =
= 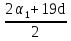 · 20 =
· 20 = 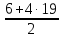 · 20 = 820.
· 20 = 820.
Ответ: 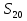 = 820.
= 820.
Задача 3. Между числами 17 и 32 вставить пять таких чисел, чтобы они вместе с данными числами составили арифметическую прогрессию.
Решение.
Имеем прогрессию: 17;  ;
; 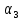 ;
;  ;
; 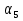 ;
; 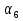 ; 32, значит
; 32, значит  = 17,
= 17, 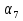 = 32. Задача сводится к определению разности прогрессии по формуле
= 32. Задача сводится к определению разности прогрессии по формуле
 =
=  + d(n – 1),
+ d(n – 1), 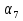 =
=  + d · 6; 32 = 17 + 6d; d = (32 – 17) : 6 = 2,5.
+ d · 6; 32 = 17 + 6d; d = (32 – 17) : 6 = 2,5.
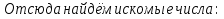
 =
=  + d = 17 + 2,5 = 19,5;
+ d = 17 + 2,5 = 19,5;
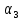 =
= + d = 19,5 + 2,5 = 22;
+ d = 19,5 + 2,5 = 22; 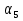 =
=  + d = 24,5 + 2,5 = 27;
+ d = 24,5 + 2,5 = 27;
 =
= 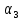 + d = 22 + 2,5 = 24,5;
+ d = 22 + 2,5 = 24,5; 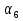 =
= 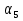 + d = 27 + 2,5 = 29,5.
+ d = 27 + 2,5 = 29,5.
Запишем прогрессию: 17; 19,5; 22; 24,5; 27; 29,5; 32.
Ответ: 17; 19,5; 22; 24,5; 27; 29,5; 32.
Задача 4. Разность арифметической прогрессии равна 4, сумма первых семи членов равна 105. Найти первый и седьмой члены прогрессии.
Решение.
Известно, что 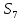 = 105, d = 4.
= 105, d = 4.
По формуле  =
=  + d(n – 1),
+ d(n – 1), 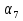 =
=  + 4 · 6;
+ 4 · 6; 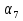 -
-  = 24.
= 24.
По формуле 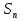 =
= 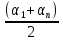 · n , 105 =
· n , 105 = 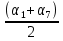 · 7;
· 7;  +
+ 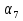 = 30.
= 30.
Составим и решим систему уравнений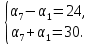
Сложим почленно оба равенства, получим 2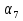 = 54,
= 54, 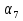 = 27, тогда
= 27, тогда  = 27 – 24 = 3.
= 27 – 24 = 3.
Ответ:  = 3,
= 3, 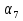 = 27.
= 27.
Задача 5. Найдите первый положительный член арифметической прогрессии -10,2; -9,5; …
Решение.
Итак,  = -10,2;
= -10,2;  = -9,5. Тогда d =
= -9,5. Тогда d =  -
-  = -9,5 – (-10,2) = 0,7.
= -9,5 – (-10,2) = 0,7.
По формуле  =
=  + d(n – 1),
+ d(n – 1),  = -10,2 + 0,7 (n – 1),
= -10,2 + 0,7 (n – 1),
 = -10,2 + 0,7n – 0,7 = 0,7n – 10,9.
= -10,2 + 0,7n – 0,7 = 0,7n – 10,9.
По условию  > 0, тогда 0,7n – 10,9 > 0, 0,7n > 10,9; n > 15
> 0, тогда 0,7n – 10,9 > 0, 0,7n > 10,9; n > 15 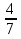 .
.
Но n 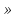 N и
N и  > 0, таким образом первый положительный член арифметической прогрессии
> 0, таким образом первый положительный член арифметической прогрессии 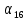 =
=  + d · 15;
+ d · 15; 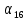 = -10,2 + 0,7 · 15 = 0,3.
= -10,2 + 0,7 · 15 = 0,3.
Ответ: 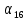 = 0,3.
= 0,3.
Задача 6. Какое наибольшее число последовательных нечётных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма осталась меньше 400?
Решение.
Последовательные нечётные числа, начиная с 1, образуют арифметическую прогрессию, у которой  = 1, d = 2.
= 1, d = 2.
Сумма n первых членов арифметической прогрессии: 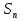 =
= 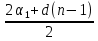 · n, тогда для заданной арифметической прогрессии:
· n, тогда для заданной арифметической прогрессии: 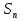 =
= 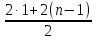 · n =
· n =
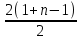 · n =
· n = 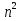 . По условию задачи
. По условию задачи 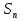
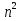
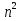 – 400
– 400
(n – 20) (n + 20) 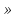 N, то n > 20, но и n ≥ 1, то получаем 1 ≤ n ≤ 19.
N, то n > 20, но и n ≥ 1, то получаем 1 ≤ n ≤ 19.
Ответ: 19 последовательных нечётных чисел, начиная с 1.
Задача 7. Арифметическая прогрессия задана формулой n-го члена  = 3n + 4. Найдите сумму членов этой арифметической прогрессии с восьмого по сорок третий включительно.
= 3n + 4. Найдите сумму членов этой арифметической прогрессии с восьмого по сорок третий включительно.
Решение.
По условию  = 3n + 4. Тогда
= 3n + 4. Тогда  = 7,
= 7,  = 10, d =
= 10, d =  -
-  =10 – 7 = 3. Сумма членов прогрессии с восьмого по сорок третий включительно находится как разность сумм
=10 – 7 = 3. Сумма членов прогрессии с восьмого по сорок третий включительно находится как разность сумм 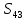 -
- 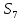 . По формуле
. По формуле 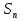 =
= 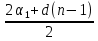 · n,
· n,
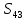 =
= 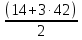 · 43 = 3010,
· 43 = 3010,
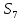 =
= 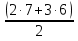 · 7 = 112. Искомая разность равна 3010 – 112 = 2898.
· 7 = 112. Искомая разность равна 3010 – 112 = 2898.
 Ответ: 2898
Ответ: 2898
Задача 8. Найдите сумму всех чётных натуральных чисел, не превосходящих 241, которые не делятся на 10.
Решение.
Пусть S – искомая сумма, 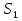 - сумма всех чётных натуральных чисел, которые не превосходят 241;
- сумма всех чётных натуральных чисел, которые не превосходят 241; 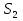 - сумма всех чётных натуральных чисел, которые делятся на 10 и не превосходят 241; тогда S =
- сумма всех чётных натуральных чисел, которые делятся на 10 и не превосходят 241; тогда S = 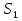 -
- 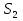 .
.
Найдём 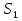 :
: 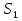 =
= 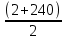 · 120 = 14520. Последовательность чисел, кратных 10 и не превосходящих 241, представляет арифметическую прогрессию, у которой
· 120 = 14520. Последовательность чисел, кратных 10 и не превосходящих 241, представляет арифметическую прогрессию, у которой  = 10,
= 10,  = 240. Найдём число членов этой прогрессии. Так как она задаётся формулой
= 240. Найдём число членов этой прогрессии. Так как она задаётся формулой  = 10n, то 10n = 240, n = 24.
= 10n, то 10n = 240, n = 24.
Найдём 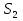 :
: 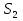 =
= 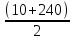 · 24 = 3000. Итак, S = 14520 – 3000 = 11520.
· 24 = 3000. Итак, S = 14520 – 3000 = 11520.
Ответ: S = 11520.
Дидактический материал.
-
Дана арифметическая прогрессия (
 ). Зная три числа из пяти (
). Зная три числа из пяти ( , d, n,
, d, n,  ,
, 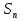 ), найдите два остальные:
), найдите два остальные:
а) Дано:  = 7, d = 4, n = 13. Найдите
= 7, d = 4, n = 13. Найдите  ,
, 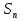 .
.
б) Дано:  = 2, d = 2, n = 40. Найдите
= 2, d = 2, n = 40. Найдите  ,
, 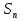 .
.
в) Дано:  = 56, d = -3, n = 11. Найдите
= 56, d = -3, n = 11. Найдите  ,
, 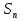 .
.
г) Дано:  = 2,
= 2,  = 87,
= 87, 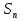 = 81. Найдите d, n.
= 81. Найдите d, n.
д) Дано:  = 21, n = 7,
= 21, n = 7, 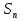 = 105. Найдите
= 105. Найдите  , d.
, d.
е) Дано:  = 10, d = 4,
= 10, d = 4,  = 50. Найдите n,
= 50. Найдите n, 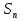 .
.
ж) Дано:  = 10, d = 4,
= 10, d = 4, 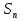 = 330. Найдите: n,
= 330. Найдите: n,  .
.
2. а) Найдите пятнадцатый член и сумму пятнадцати членов арифметической прогрессии: 2; 5; 8; … .
б) Найдите первый член и разность арифметической прогрессии, если 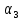 = 25,
= 25, 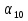 = -3.
= -3.
в) Сколько нужно взять членов арифметической прогрессии, чтобы сумма их равнялась 54, если  = 9,
= 9, 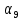 = - 6?
= - 6?
г) В арифметической прогрессии (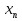 ) известно, что
) известно, что 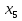 = - 1,5;
= - 1,5; 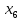 =
= 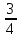 .
.
Найдите 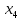 +
+ 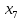 .
.
д) Найдите сумму членов с третьего по десятый включительно арифметической прогрессии: -3; -1; … .
е) Сумма трёх первых членов арифметической прогрессии (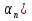 равна 6,
равна 6,  = 5. Найдите
= 5. Найдите 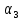 и разность прогрессии.
и разность прогрессии.
3. а) Какое из следующих чисел является членом арифметической прогрессии:
6; 12; 18; 24; …?
-
303, 2) 109, 3) 106, 4) 96.
б) Какое из чисел является членом арифметической прогрессии: 3; 6; 9; 12; …?
1) 83, 2) 95, 3) 100, 4) 102.
4. Какая из следующих последовательностей является арифметической прогрессией?
а) Последовательность натуральных степеней числа 2.
б) Последовательность натуральных чисел, кратных 7.
в) Последовательность квадратов натуральных чисел.
г) Последовательность чисел, обратных натуральным.
5. В арифметической прогрессии 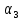 = 5,
= 5,  = 7. Найдите сумму первых десяти членов этой прогрессии.
= 7. Найдите сумму первых десяти членов этой прогрессии.
6. а) Сумма 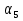 +
+ 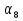 = 14. Найдите сумму первых двенадцати членов этой прогрессии.
= 14. Найдите сумму первых двенадцати членов этой прогрессии.
б) Сумма 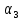 +
+ 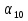 = - 8. Найдите сумму первых двенадцати членов этой прогрессии.
= - 8. Найдите сумму первых двенадцати членов этой прогрессии.
7. Космический корабль за 1 секунду проходит 50м, а за каждую следующую секунду на 80м больше, чем за предыдущую. Сколько метров он пройдёт с 10-й по 15-ую секунды включительно?
8. а) Арифметическая прогрессия задана формулой n-го члена  = 3n + 5. Найдите сумму членов арифметической прогрессии с десятого по сорок пятый включительно.
= 3n + 5. Найдите сумму членов арифметической прогрессии с десятого по сорок пятый включительно.
б) Арифметическая прогрессия задана формулой n-го члена  = 2n + 3. Найдите сумму членов арифметической прогрессии с двенадцатого по сорок пятый включительно.
= 2n + 3. Найдите сумму членов арифметической прогрессии с двенадцатого по сорок пятый включительно.
в) Арифметическая прогрессия задана формулой n-го члена  = 3n + 2. Найдите сумму членов арифметической прогрессии с нечётными номерами, меньшими 50.
= 3n + 2. Найдите сумму членов арифметической прогрессии с нечётными номерами, меньшими 50.
9. а) Сколько отрицательных членов в арифметической прогрессии:
-38,5; -35,8; …?
б) Сколько положительных членов в арифметической прогрессии:
96,4; 91,8; … .
в) Найдите первый отрицательный член арифметической прогрессии:
12,5; 11,2; … .
г) Найдите сумму всех отрицательных членов арифметической прогрессии:
-7,1; - 6,3;… .
д) Найдите сумму всех положительных членов арифметической прогрессии: 6,3; 5,8; … .
е) Какое наименьшее число последовательных нечётных чисел, начиная с 1, нужно сложить, чтобы получившаяся сумма оказалась больше 900?
10. а) Найдите сумму всех натуральных чисел, которые делятся на 9 и не превосходят 400.
б) Найдите сумму всех натуральных чисел, не превосходящих 170, которые делятся на 6.
11. а) Существует ли арифметическая прогрессия, в которой 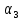 =7,
=7, 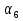 = 13,
= 13,
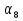 = 17?
= 17?
б) Существует ли арифметическая прогрессия, в которой  = 8,
= 8, 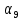 = -7,
= -7,
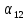 = -17?
= -17?
12. а) Найдите сумму арифметической прогрессии, если  +
+ 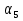 = 24,
= 24,  ·
· 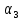 = 60.
= 60.
б) Сумма второго, четвёртого и шестого членов арифметической прогрессии равна 18, а их произведение равно 120. Найдите первый член прогрессии.
13. а) В угловом секторе стадиона в первом ряду 7 мест, а в каждом следующем
на 2 больше, чем в предыдущем. Сколько мест в 26 ряду?
б) На первую клетку шахматной доски положили 1 зерно, а на каждую следующую на 2 зерна больше, чем на предыдущую. Сколько зёрен положили на последнюю клетку?
14. а) Укажите наиболее близкий к нулю член арифметической прогрессии:
22,7; 21,4; …
б) Укажите наиболее близкий к нулю член арифметической прогрессии:
-15,1; -14,4; …
15. Найдите сумму первых двадцати членов арифметической прогрессии ( ), если
), если
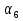 +
+ 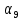 +
+ 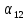 +
+ 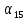 = 20.
= 20.
16. Найдите сумму всех двузначных натуральных чисел.
Проверочная работа.
Вариант 1.
-
Последовательность задана формулой
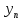 = 5n + 4. Найдите:
= 5n + 4. Найдите:
а) 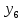 ________________
________________ 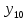 _____________________
_____________________
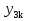 ________________
________________ 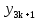 ___________________
___________________
б) номер члена последовательности, равного 109: ____________________
________________________________________________________________
-
В арифметической прогрессии
 = 3,
= 3,  = -5. Запишите формулу общего члена.___________________________________________________________
= -5. Запишите формулу общего члена.___________________________________________________________
-
В арифметической прогрессии (
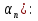
 = - 2, d = 10,
= - 2, d = 10,  = 478. Найдите n. ________________________________________________________________
= 478. Найдите n. ________________________________________________________________ -
В арифметической прогрессии (
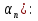
 = 6, d = - 4. Найдите:
= 6, d = - 4. Найдите:
а) 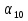 _________________________________________________________
_________________________________________________________
б) 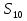 _________________________________________________________
_________________________________________________________
-
Шар, скатывающийся по наклонному желобу, в первую секунду проходит 0,4м, а в каждую последующую секунду на 0,4 больше, чем в предыдущую. Сколько времени будет двигаться шар по четырёхметровому желобу? ____________________________________________________________________________________________________________________________________
-
Найдите
 и d арифметической прогрессии с положительными членами, если:
и d арифметической прогрессии с положительными членами, если:
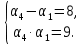
__________________________________________________________________________________________________________________________________
-
В арифметической прогрессии: - 63; -58; -53; … , найдите сумму всех отрицательных чисел.
__________________________________________________________________________________________________________________________________
-
В арифметической прогрессии первый член равен 3, третий 7. Найдите разность между 61-м и 32-м членами этой арифметической прогрессии.
__________________________________________________________________________________________________________________________________
-
При каком значении х данные числа образуют арифметическую прогрессию?
а) 2х + 3; 5х + 2; 10х + 5: __________________________________________________________________________________________________________________________________
б) 3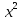 + 6;
+ 6; 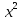 + 4; 3
+ 4; 3 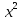 + 3х + 1: __________________________________________________________________________________________________________________________________
+ 3х + 1: __________________________________________________________________________________________________________________________________
10. Найдите сумму всех натуральных чисел, не превосходящих 150, которые делятся на 5: ____________________________________________________________
______________________________________________________________________
Вариант 2.
-
Последовательность задана формулой
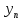 = 6 - 4n. Найдите:
= 6 - 4n. Найдите:
а) 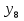 ____________________
____________________ 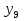 _________________________
_________________________
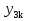 ____________________
____________________ 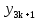 _______________________
_______________________
б) номер члена последовательности, равного ―242:__________________ _______________________________________________________________
-
В арифметической прогрессии
 = -5,
= -5,  = 2. Запишите формулу общего члена._________________________________________________________
= 2. Запишите формулу общего члена._________________________________________________________
-
В арифметической прогрессии (
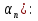
 = 2, d = 4,
= 2, d = 4,  = - 42. Найдите n. _________________________________________________________________
= - 42. Найдите n. _________________________________________________________________ -
В арифметической прогрессии (
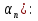
 = 3, d = - 2. Найдите:
= 3, d = - 2. Найдите:
а) 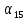 ___________________________________________________________
___________________________________________________________
б) 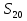 ___________________________________________________________
___________________________________________________________
-
Шар, скатывающийся по наклонному желобу, в первую секунду проходит 0,5м, а в каждую последующую секунду на 0,5 больше, чем в предыдущую. Сколько времени будет двигаться шар по пятиметровому желобу? __________________________________________________________________________________________________________________________________
-
Найдите
 и d арифметической прогрессии с положительными членами, если:
и d арифметической прогрессии с положительными членами, если:
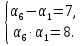
__________________________________________________________________________________________________________________________________
-
В арифметической прогрессии: - 9,6; - 8,3; -7; … , найдите сумму всех отрицательных чисел.
__________________________________________________________________________________________________________________________________
-
В арифметической прогрессии первый член равен 5, пятый 7. Найдите разность между 79-м и 42-м членами этой арифметической прогрессии.
__________________________________________________________________________________________________________________________________
-
При каком значении х данные числа образуют арифметическую прогрессию?
а) 3х - 8; 5х + 4; 6х + 2: __________________________________________________________________________________________________________________________________
б) 3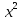 - 8; 7
- 8; 7 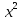 - 3; 9
- 3; 9 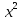 - 3х + 7: __________________________________________________________________________________________________________________________________
- 3х + 7: __________________________________________________________________________________________________________________________________
-
Найдите сумму всех натуральных чисел, не превосходящих 200, которые делятся на 8: _____________________________________________________
_________________________________________________________________
ТЕСТЫ.
Вариант 1.
-
Из следующих чисел выберите то, которое не является членом арифметической прогрессии:
 = -3n + 7.
= -3n + 7.
А) - 8; Б) - 14; В) - 23; Г) 10.
2. Дана арифметическая прогрессия: ―3,2; 1; … .
Найдите пятый член этой прогрессии.
А) 12,8; Б) 16,6; В) 13,6; Г) 14,2.
3. В арифметической прогрессии ( ):
):  = 32,2;
= 32,2; 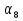 = 7,8. Найдите сумму первых восьми членов этой прогрессии
= 7,8. Найдите сумму первых восьми членов этой прогрессии
А) 32,2; Б) 204; В) 160; Г) 96.
4. В арифметической прогрессии ( ):
):  = - 2,4; d = 1,5.
= - 2,4; d = 1,5.
Найдите сумму первых шести членов этой прогрессии.
А) -8,1; Б) 7,2; В) 8,1; Г) 16,2.
5. Второй и десятый члены арифметической прогрессии равны: 38 и ―18 соответственно. Найдите пятнадцатый член прогрессии.
А) - 48; Б) - 53; В) - 63; Г) - 57.
6. Сумма третьего и одиннадцатого членов арифметической прогрессии равна ―14,8. Найдите седьмой член этой прогрессии.
А) - 12,4; Б) - 7,4; В) - 8,6; Г) -10,2.
7. Найдите первый отрицательный член арифметической прогрессии, заданной формулой n-го члена:  = 204 - 15n.
= 204 - 15n.
А) - 8; Б) - 6; В) - 4; Г) - 9.
8. Найдите разность арифметической прогрессии d, если 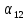 -
-  = 58,4.
= 58,4.
А) 7,3; Б) 8,4; В) 6,8; Г) 8,3.
9. Третий член арифметической прогрессии равен 17.
Найдите сумму первый пяти членов арифметической прогрессии.
А) 85; Б) 65; В) 77; Г) 95.
10. Сумма пятого и девятнадцатого членов арифметической прогрессии
равна 14,6. Найдите сумму первых двадцати трёх членов этой прогрессии.
А) 189,4; Б) 167,9; В) 153,6; Г) 190,9.
11. Разность четырнадцатого и пятого членов арифметической прогрессии
равна 18, а сумма пятого и второго членов этой прогрессии равна 2.
Найдите сумму первых пятнадцати членов этой прогрессии.
А) 150; Б) 148; В) 136; Г) 102.
Вариант 2.
-
Из следующих чисел выберите то, которое не является членом арифметической прогрессии:
 = 2 + 3
= 2 + 3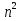 .
.
А) 29; Б) 5; В) 20; Г) 14.
2. Дана арифметическая прогрессия: 27; 24; … .
Найдите двадцать первый член этой прогрессии.
А) - 46; Б) - 33; В) 12; Г) -18.
3. В арифметической прогрессии ( ):
):  = 46,7;
= 46,7; 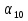 = 3,3. Найдите сумму первых десяти членов этой прогрессии
= 3,3. Найдите сумму первых десяти членов этой прогрессии
А) 240; Б) 180; В) 260; Г) 250.
4. В арифметической прогрессии ( ):
):  = - 6,3; d = 1,2.
= - 6,3; d = 1,2.
Найдите сумму первых восьми членов этой прогрессии.
А) 12; Б) -12,8; В) 14,6; Г) - 16,8.
5. Третий и восьмой члены арифметической прогрессии равны: 27 и ―18 соответственно. Найдите тринадцатый член прогрессии.
А) -38; Б) - 45; В) - 53; Г) -43.
6. Сумма пятого и тринадцатого членов арифметической прогрессии
равна ―19,6. Найдите девятый член этой прогрессии.
А) - 9,8; Б) - 10,2; В) - 8,8; Г) - 12,3.
7. Найдите первый положительный член арифметической прогрессии, заданной формулой n-го члена:  = 16n - 209.
= 16n - 209.
А) 12; Б) 15; В) 21; Г) 19.
8. Найдите разность арифметической прогрессии d, если 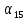 -
- 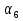 = 25,2.
= 25,2.
А) 2,8; Б) 6,4; В) 4,8; Г) 5,3.
9. Девятый член арифметической прогрессии равен 9.
Найдите сумму первый семнадцати членов арифметической прогрессии.
А) 146; Б) 163; В) 153; Г) 172.
10. Сумма четвёртого и двадцать первого членов арифметической прогрессии равна 17,5. Найдите сумму первых двадцати членов этой прогрессии.
А) 193,5; Б) 144,5; В) 210; Г) 175,5.
11. Разность двенадцатого и шестого членов арифметической прогрессии
равна 24, а сумма шестого и третьего членов этой прогрессии равна 4.
Найдите сумму первых четырнадцати членов этой прогрессии.
А) 148; Б) 196; В) 204; Г) 162.
Самостоятельная работа. Формула n-го члена
Вариант 1. Уровень А.
-
Составьте формулу n-го члена арифметической прогрессии (
 ) и
) и
найдите 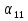 , если
, если = 3,6; d = - 0,6.
= 3,6; d = - 0,6.
-
Найдите разность арифметической прогрессии (
 ), если
), если  = -1,6;
= -1,6;
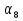 = - 3,7.
= - 3,7.
-
Найдите первый член арифметической прогрессии (
 ), если
), если 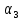 = 15;
= 15;
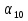 = - 18,6.
= - 18,6.
-
Дана арифметическая прогрессия: - 25; - 21; … . Определите под каким номером в эту прогрессию входит число 3.
Уровень Б.
-
Дана арифметическая прогрессия: - 16,5; - 14,3; … . Найдите двадцать первый член и разность арифметической прогрессии.
-
Найдите первый член и разность арифметической прогрессии (
 ),
),
если  = 2,6;
= 2,6; 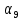 = 8,9.
= 8,9.
-
Найдите номер члена арифметической прогрессии (
 ) равного 62, если
) равного 62, если
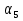 = - 6; d = 4.
= - 6; d = 4.
-
Арифметическая прогрессия задана формулой:
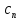 = 19n – 106. Найдите первый положительный член прогрессии.
= 19n – 106. Найдите первый положительный член прогрессии.
Уровень В.
-
Бригада изготовила в январе 48 деталей, а в каждый следующий месяц изготовляла на 7 деталей больше, чем в предыдущий. Сколько деталей изготовила бригада в декабре?
-
Найдите пятнадцатый член арифметической прогрессии (
 ), если
), если  = -7,2;
= -7,2; 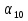 = 1,2.
= 1,2. -
Между числами 2,6 и ―10,2 вставьте три числа так, чтобы они вместе с данными числами составили арифметическую прогрессию.
-
Найдите значения х, при которых числа : х – 1; 4х – 3;
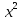 + 1 составляют арифметическую прогрессию.
+ 1 составляют арифметическую прогрессию.
Вариант 2. Уровень А.
-
Составьте формулу n-го члена арифметической прогрессии (
 ) и
) и
найдите 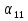 , если
, если = - 5,1; d = 0,4.
= - 5,1; d = 0,4.
-
Найдите разность арифметической прогрессии (
 ), если
), если  = 5,3;
= 5,3; 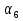 = 1,8.
= 1,8. -
Найдите первый член арифметической прогрессии (
 ), если
), если 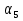 = 18;
= 18;
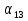 = 26,8.
= 26,8.
-
Дана арифметическая прогрессия: 43; 40; … . Определите под каким номером в эту прогрессию входит число 1.
Уровень Б.
-
Дана арифметическая прогрессия: 24,6; 23,1; … . Найдите двадцать первый член и разность арифметической прогрессии.
-
Найдите первый член и разность арифметической прогрессии (
 ),
),
если 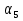 = - 0,7;
= - 0,7; 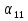 = 8,9.
= 8,9.
-
Найдите номер члена арифметической прогрессии (
 ) равного 66,
) равного 66,
если 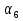 = - 4; d = 7.
= - 4; d = 7.
-
Арифметическая прогрессия задана формулой:
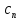 = 121 - 9n. Найдите первый отрицательный член прогрессии.
= 121 - 9n. Найдите первый отрицательный член прогрессии.
Уровень В.
-
Мастерская выполнила в январе 36 заказов, а в каждый последующий месяц увеличивала производительность на 12 заказов. Сколько заказов выполнила мастерская в октябре месяце?
-
Найдите пятнадцатый член арифметической прогрессии (
 ),
),
если 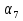 = 3,8;
= 3,8; 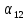 = 7, 3.
= 7, 3.
-
Между числами ―16,5 и 61 вставьте три числа так, чтобы они вместе с данными числами составили арифметическую прогрессию.
-
Найдите значения х, при которых числа : х + 1; 2х + 1;
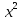 - 3 составляют арифметическую прогрессию.
- 3 составляют арифметическую прогрессию.
Самостоятельная работа. Формула суммы n первых членов арифметической прогрессии.
Вариант 1. Уровень А.
-
Найдите сумму двенадцати первых членов арифметической прогрессии:
- 9; - 4; … .
-
В первый день магазин продал 27кг яблок, а в каждый следующий день продавал на 3кг яблок больше, чем в предыдущий. Сколько яблок продал магазин за 10 дней?
-
Найдите сумму натуральных чисел, не превосходящих 50.
-
Дана арифметическая прогрессия (
 ), где
), где  = 6n – 2. Найдите сумму её членов с восьмого по восемнадцатый включительно.
= 6n – 2. Найдите сумму её членов с восьмого по восемнадцатый включительно.
Уровень Б.
-
Найдите сумму пятнадцати первых членов арифметической прогрессии (
 ), если
), если  = 5n + 3.
= 5n + 3. -
Найдите сумму девяти первых членов арифметической прогрессии (
 ), если
), если 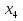 = -5;
= -5; 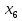 = -3, 4.
= -3, 4. -
Найдите сумму чётных чисел не превосходящих 50.
-
При каком значении х числа х + 3; 2х – 1 и
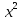 - 3 образуют положительную арифметическую прогрессию?
- 3 образуют положительную арифметическую прогрессию?
Уровень В.
-
В арифметической прогрессии 48; 44; … найдите сумму всех её положительных членов.
-
Найдите сумму всех двузначных натуральных чисел, кратных 5.
-
Найдите
 и d арифметической прогрессии, в которой
и d арифметической прогрессии, в которой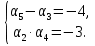
-
В арифметической прогрессии (
 ) :
) : 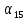 = 18. Найдите
= 18. Найдите 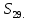
-
Найдите сумму:
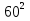 -
- 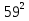 +
+ 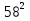 -
- 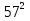 +
+ 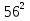 -
- 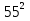 + … +
+ … + 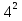 -
- 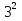 +
+ 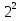 -
- 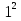 .
.
Вариант 2. Уровень А.
-
Найдите сумму двенадцати первых членов арифметической прогрессии:
26; 20; … .
-
За первую секунду движения тело прошло 22м, а в каждую последующую проходило на 4м больше, чем в предыдущую. Найдите путь, пройденный телом за 8 секунд.
-
Найдите сумму натуральных чисел, не превосходящих 60.
-
Дана арифметическая прогрессия (
 ), где
), где  = 3n + 4. Найдите сумму её членов с восьмого по восемнадцатый включительно.
= 3n + 4. Найдите сумму её членов с восьмого по восемнадцатый включительно.
Уровень Б.
-
Найдите сумму пятнадцати первых членов арифметической прогрессии (
 ), если
), если  = 6n - 5.
= 6n - 5. -
Найдите сумму девяти первых членов арифметической прогрессии (
 ), если
), если 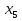 = 8;
= 8; 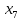 = 10,6.
= 10,6. -
Найдите сумму нечётных чисел не превосходящих 50.
-
При каком значении х числа х + 1; 3х + 5 и
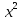 + 3 образуют положительную арифметическую прогрессию?
+ 3 образуют положительную арифметическую прогрессию?
Уровень В.
-
В арифметической прогрессии -72; - 66; … найдите сумму всех её отрицательных членов.
-
Найдите сумму всех двузначных натуральных чисел, кратных 9.
-
Найдите
 и d арифметической прогрессии, в которой
и d арифметической прогрессии, в которой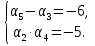
-
В арифметической прогрессии (
 ) :
) : 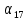 = 24. Найдите
= 24. Найдите 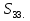
-
Найдите сумму:
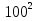 -
- 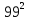 +
+ 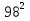 -
- 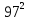 +
+ 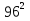 -
- 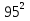 + … +
+ … + 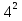 -
- 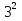 +
+ 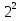 -
- 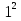 .
.
Контрольная работа.
Арифметическая прогрессия.
Вариант 1.
-
В арифметической прогрессии
 = 8n – 5. Найдите
= 8n – 5. Найдите  ,
, 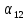 .
. -
В арифметической прогрессии
 = - 5,
= - 5,  = 2. Напишите формулу общего члена прогрессии и найдите
= 2. Напишите формулу общего члена прогрессии и найдите 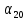 .
. -
В арифметической прогрессии (
 ), найдите сумму первых двадцати членов, если
), найдите сумму первых двадцати членов, если  = - 1,
= - 1, 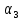 = 1.
= 1. -
Найдите сумму членов с третьего по десятый включительно арифметической прогрессии (
 ): - 3; - 1; … .
): - 3; - 1; … . -
Сумма четвёртого и десятого членов арифметической прогрессии равна 6, а их произведение равно 8. Найдите сумму пятнадцати первых членов этой прогрессии.
Вариант 2.
-
В арифметической прогрессии
 = 16 – 5n. Найдите
= 16 – 5n. Найдите 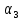 ,
, 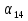 .
. -
В арифметической прогрессии
 = 6,
= 6,  = - 1. Напишите формулу общего члена прогрессии и найдите
= - 1. Напишите формулу общего члена прогрессии и найдите 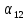 .
. -
В арифметической прогрессии (
 ), найдите сумму первых двадцати членов, если
), найдите сумму первых двадцати членов, если  = 8,
= 8, 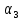 = 2.
= 2. -
Найдите сумму членов с третьего по девятый включительно арифметической прогрессии (
 ): 2; 7; … .
): 2; 7; … . -
Сумма третьего и девятого членов арифметической прогрессии равна 6, а их произведение равно
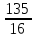 . Найдите сумму пятнадцати первых членов этой прогрессии.
. Найдите сумму пятнадцати первых членов этой прогрессии.
Вариант 3.
-
В арифметической прогрессии
 = 3n + 4. Найдите
= 3n + 4. Найдите 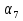 ,
, 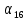 .
. -
В арифметической прогрессии
 = 3,
= 3,  = - 2. Напишите формулу общего члена прогрессии и найдите
= - 2. Напишите формулу общего члена прогрессии и найдите 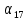 .
. -
В арифметической прогрессии (
 ), найдите сумму первых двадцати членов, если
), найдите сумму первых двадцати членов, если  = 7,
= 7, 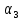 = 11.
= 11. -
Найдите сумму членов с пятого по шестнадцатый включительно арифметической прогрессии (
 ): 4; 7; 10; … .
): 4; 7; 10; … . -
Найдите сумму всех натуральных чисел, кратных 4 и не превосходящих 202.
Вариант 4.
-
В арифметической прогрессии
 = 3n + 4. Найдите
= 3n + 4. Найдите 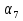 ,
, 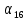 .
. -
В арифметической прогрессии
 = 15,
= 15,  = 9. Напишите формулу общего члена прогрессии и найдите
= 9. Напишите формулу общего члена прогрессии и найдите 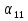 .
. -
В арифметической прогрессии (
 ), найдите сумму первых тридцати членов, если
), найдите сумму первых тридцати членов, если  = 6,
= 6, 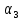 = 2.
= 2. -
Найдите сумму членов с четвёртого по двенадцатый включительно арифметической прогрессии (
 ): 3; 1; - 1; … .
): 3; 1; - 1; … . -
Найдите сумму первых шестнадцати чётных натуральных чисел.
§ 3. Геометрическая прогрессия.
Справочный материал.
-
Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же не равное нулю число, называется геометрической прогрессией.
-
Обозначают (
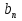 ) :
) : 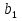 ,
, 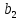 ,
, 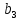 , …,
, …, 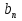 , … .
, … . -
Отношение любого её члена к предшествующему равно одному и тому же числу, т. е.
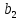 :
: 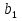 =
= 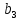 :
: 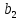 = … =
= … = 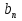 :
: 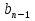 =
= 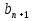 :
: 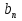 = … . Это число называют знаменателем геометрической прогрессии и обозначают буквой q.
= … . Это число называют знаменателем геометрической прогрессии и обозначают буквой q. -
Для того чтобы задать геометрическую прогрессию (
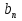 ), достаточно знать её первый член
), достаточно знать её первый член 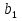 и знаменатель q.
и знаменатель q. -
Если q > 1,
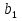 > 0, то геометрическая прогрессия является возрастающей;
> 0, то геометрическая прогрессия является возрастающей;
если 0 и 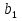 > 0, то геометрическая прогрессия является убывающей;
> 0, то геометрическая прогрессия является убывающей;
если q = 1, то имеем постоянную последовательность;
при q – геометрическая прогрессия не является монотонной.
-
Например:
1; 3; 9; 27; … , здесь q = 3, 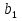 = 1> 0 – прогрессия возрастающая;
= 1> 0 – прогрессия возрастающая;
1; 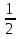 ;
; 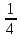 ;
; 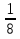 ; …, здесь q =
; …, здесь q = 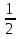 ,
, 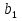 = 1> 0 – прогрессия убывающая;
= 1> 0 – прогрессия убывающая;
2; 2; 2; 2; …, здесь q = 1, то имеем постоянную последовательность;
1; - 2; 4; - 8; …, здесь q = - 2, последовательность не монотонная.
-
Последовательность (
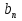 ) является геометрической тогда и только тогда, когда каждый её член, начиная со второго, есть среднее геометрическое соседних с ним членов, т. е.
) является геометрической тогда и только тогда, когда каждый её член, начиная со второго, есть среднее геометрическое соседних с ним членов, т. е. 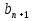 2 =
2 = 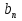 ·
· 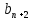 , где n
, где n 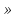 N, n ≥ 2.
N, n ≥ 2. -
Формулы n-го члена геометрической прогрессии:
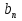 =
= 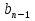 · q и
· q и 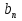 =
= 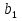 ·
· 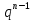 .
.
-
Произведение членов, равноотстоящих от концов прогрессии есть величина постоянная:
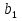 ·
· 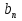 =
= 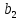 ·
· 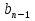 = … .
= … . -
Формулы суммы n первых членов геометрической прогрессии:
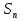 =
= 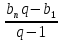 , (q
, (q 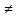 1) и
1) и 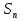 =
= 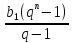 , (q
, (q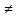 1).
1). -
Бесконечная геометрическая
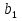 ,
, 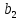 ,
, 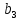 , …,
, …, 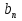 , … , прогрессия знаменатель которой |q| называется бесконечной геометрической прогрессией. Если |q| то члены бесконечной геометрической прогрессии стремятся к нулю, когда их номера неограниченно возрастают.
, … , прогрессия знаменатель которой |q| называется бесконечной геометрической прогрессией. Если |q| то члены бесконечной геометрической прогрессии стремятся к нулю, когда их номера неограниченно возрастают. -
Под суммой S бесконечной геометрической прогрессии
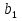 ,
, 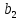 ,
, 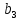 , …,
, …, 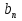 , … , у которой |q|
, … , у которой |q| 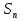 ), где
), где 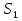 =
= 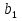 ,
,
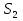 =
= 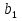 +
+ 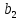 ,
, 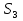 =
= 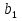 +
+ 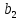 +
+ 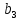 ; … ;
; … ; 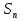 =
= 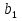 +
+ 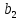 +
+ 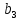 + … +
+ … + 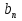 . При этом имеет место равенство: S =
. При этом имеет место равенство: S = 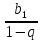 , при |q|
, при |q|
Здесь представлен конспект к уроку на тему «Арифметическая и геометрическая прогрессии», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

