Слайд 1Преобразование сигналов в нелинейных радиотехнических цепях
Радиотехнические цепи и сигналы
Слайд 2Рекомендуемая литература
В.И. Нефёдов «Основы радиоэлектроники и связи», 2009 г С.И. Баскаков «Радиотехнические цепи и сигналы», 2003 г. С.И. Баскаков «Радиотехнические цепи и сигналы. Руководство к решению задач», 2002 г. 4. М.Т. Иванов, А.Б. Сергиенко, В.Н. Ушаков, «Теоретические основы радиотехники», 2002 г. 5. М.П. Медиченко, В.П. Литвинов «Радиотехнические цепи и сигналы, т.1; 2», 2011 г.
Слайд 3Аппроксимация характеристик нелинейных элементов
Нелинейную цепь можно определить не только по входящим в неё элементам, но и по внешним признакам, к числу которых при гармоническом входном сигнале ? вх (?)относят:
отличие от синусоидальной формы выходного сигнала ? вых (?); появление в спектре выходного колебания гармоник входного сигнала; нелинейность передаточной амплитудной характеристики; зависимость фазы усиленного сигнала от амплитуды.
Слайд 4Известны и используют следующие методы анализа нелиней-ных цепей при прохождении через них детерминированных сигналов:
линеаризация характеристик нелинейного элемента (НЭ) при фильтрации высших гармоник сигнала на выходе цепи; аналитические, как правило, приближенные способы решения системы нелинейных уравнений, описывающих работу устройства; спектральный, оценивающий нелинейные свойства цепи по спектру выходного сигнала; численные способы решения системы нелинейных уравнений с помощью компьютера;
Слайд 5Наиболее часто используют метод анализа нелинейных цепей, основанный на линеаризации характеристик НЭ при фильтрации высших гармоник сигнала на выходе цепи. Линеаризация (от лат. linearis – линейный) – метод приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяют анализом линейной системы, в некотором смысле эквивалент-ной исходной.
Слайд 6Нелинейные элементы
В качестве примера нелинейных цепей, точнее элементов, можно привести полупроводниковый выпрямительный диод, оставляющий от синусоидального сигнала только однополярные (положительные или отрицательные) полусинусоиды, или трансформатор, насыщение сердечника которого магнитным полем приводит к «затуплению» вершин синусоиды (а с точки зрения частотного спектра, это сопровождается появлением гармоник основной частоты, а иногда и частот меньшей в кратное число раз основной частоты – субгармоник).
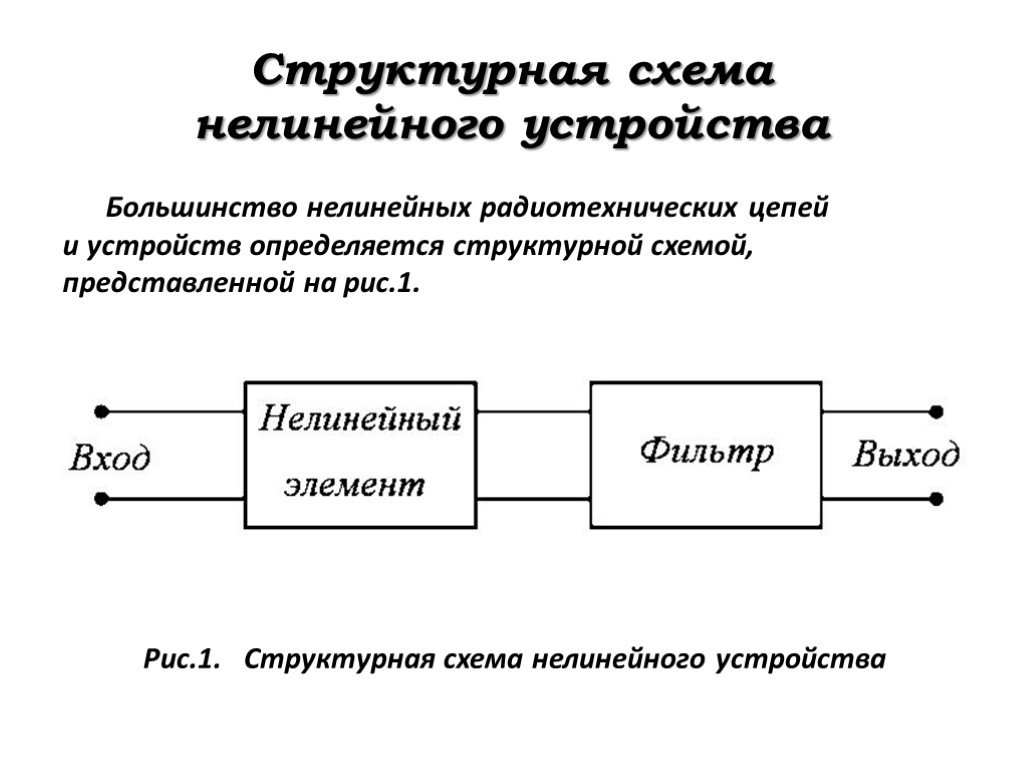
Слайд 7Структурная схема нелинейного устройства
Большинство нелинейных радиотехнических цепей и устройств определяется структурной схемой, представленной на рис.1.
Рис.1. Структурная схема нелинейного устройства
Слайд 8Принцип работы нелинейного устройства
Согласно этой схеме, входной сигнал непосредственно воздействует на нелинейный элемент, к выходу которого подключён фильтр (линейная цепь). В этих случаях процесс в радиоэлектронной нелинейной цепи можно охарактеризовать двумя независимыми друг от друга операциями.
В результате первой операции в безынерционном нелинейном элементе происходит такое преобразование формы входного сигнала, при котором в его спектре появляются новые гармонические составляющие.
Слайд 9Вторую операцию осуществляет фильтр, выделяющий нужные спектральные составляющие преобразованного входного сигнала. Меняя параметры входных сигналов и используя различные нелинейные элементы и фильтры, можно осуществлять требуемую трансформацию спектра. К такой удобной теоретической модели сводятся многие схемы модуляторов, детекторов, автогенераторов, выпрямителей, умножителей, делителей и преобразователей частоты.
![Вольт-амперная характеристика нелинейного устройства. Нелинейные цепи характеризуются сложной зависимостью между входным сигналом ? вх (?) и выходной реакцией ? вых ? , которую в общем виде можно записать так: ? вых ? =?[ ? вх (?)]. В нелинейных цепях с безынерционными НЭ в качестве воздейст-вия наи Вольт-амперная характеристика нелинейного устройства. Нелинейные цепи характеризуются сложной зависимостью между входным сигналом ? вх (?) и выходной реакцией ? вых ? , которую в общем виде можно записать так: ? вых ? =?[ ? вх (?)]. В нелинейных цепях с безынерционными НЭ в качестве воздейст-вия наи](https://prezentacii.org/upload/cloud/19/09/165095/images/thumbs/screen10.jpg)
Слайд 10Вольт-амперная характеристика нелинейного устройства
Нелинейные цепи характеризуются сложной зависимостью между входным сигналом ? вх (?) и выходной реакцией ? вых ? , которую в общем виде можно записать так:
? вых ? =?[ ? вх (?)]
В нелинейных цепях с безынерционными НЭ в качестве воздейст-вия наиболее удобно рассматривать входное напряжение ? вх (?), а отклика – выходной ток ? вых ? , связь между которыми определя-етсянелинейной функциональной зависимостью:
? вых ? =?[ ? вх (?)]
....................... (1)
Данное соотношение аналитически может представлять собой обычную вольтамперную характеристику НЭ.

Слайд 11Аппроксимация вольт-амперной характеристики
Задача аппроксимации – представление исходных сложных функций ?(?) простыми и удобными для практического использования относительно простыми функциями ?(?) (или их набором) таким образом, чтобы отклонение ?(?) от ?(?) в области её задания было наименьшим по определённому критерию приближения.
Функции ?(?) называют функциями аппроксимации. Нахождение аналитической функции по экспе-риментальнойвольт-амперной характеристике нелинейного элемента называют аппроксимацией.
Слайд 12В радиотехнике и теории передачи информации использу-ются несколько способов аппроксимации характеристик НЭ – степеннáя, показательная, кусочно-линейная (линейно-ломаная). Наибольшее распространение получили аппроксимация степенным полиномом и кусочно-линейная аппроксимация сложных функций.

Слайд 13Аппроксимация ВАХ степенным полиномом
Наиболее часто при аппроксимации в качестве степеннóго полинома используют ряд Тейлора:
? ? = ? ? + ? ? ?− ? ? + ? ? (?− ? ? ) ? +…+ ? ? (?− ? ? ) ?
....... (2)
где: ? ? , ? ? , ? ?, … , ? ? – постоянные коэффициенты;
? ?
– значение напряжения ?, относительно которого ведётся разложение в ряд и называемое рабочей точкой .
Постоянные коэффициенты ряда Тейлора определяются формулой
............ (3)
Данный вид аппроксимации особенно эффективен при малых амплитудах входных сигналов (как правило, доли вольта) в тех случаях, когда характеристика НЭ имеет вид гладкой кривой, т.е. кривая и её производные непрерывны и не имеют скачков.
? ? = ? ?! · ? ? ? ? ? ? ?= ? ?

Слайд 14Оптимальное число членов ряда берётся в зависимости от тре-буемой точности аппроксимации. Чем больше выбрано членов ряда, тем точнее аппроксимация. Аппроксимацию характеристик обычно удаётся достаточно точно осуществить полиномом не выше второй-третьей степени.
Для отыскания неизвестных коэффициентов ряда (2) необходимо задаться диапазоном ? ? , ? ? нескольких возможных значений напряжения ? и положением рабочей точки ? ? в этом диапазоне.

Слайд 15Если требуется определить ? коэффициентов ряда, то на заданной характеристике выбирается ?+?точек со своими координатами (? ? , ? ? ). Для упрощения расчётов одну точку совмещают с рабочей точкой ? ? , имеющей координаты (? ? , ? ? ); ещё две точки выбираются на границах диапазона ?= ? ? и ?= ? ? .
Остальные точки располагают произвольно, но с учётом важности аппроксимируемого участка ВАХ. Подставляя координаты выбранных точек в формулу (2), составляют систему из ?+?уравнений, которая решается относительно известных коэффициентов ? ? ряда Тейлора.

Слайд 16Кусочно-линейная аппроксимация ВАХ
Когда на нелинейный элемент радиоэлектронной цепи воздействует сигнал значительной амплитуды, реальную ВАХ нелинейного элемента можно аппроксимировать кусочно-линейной линией, состоящей из нескольких отрезков прямых с различными углами наклона к оси абсцисс. Данная аппрокси-мациясвязана непосредственно с с двумя важными параметрами нелинейного элемента – напряжением начала характеристики ? н и её крутизной ?.
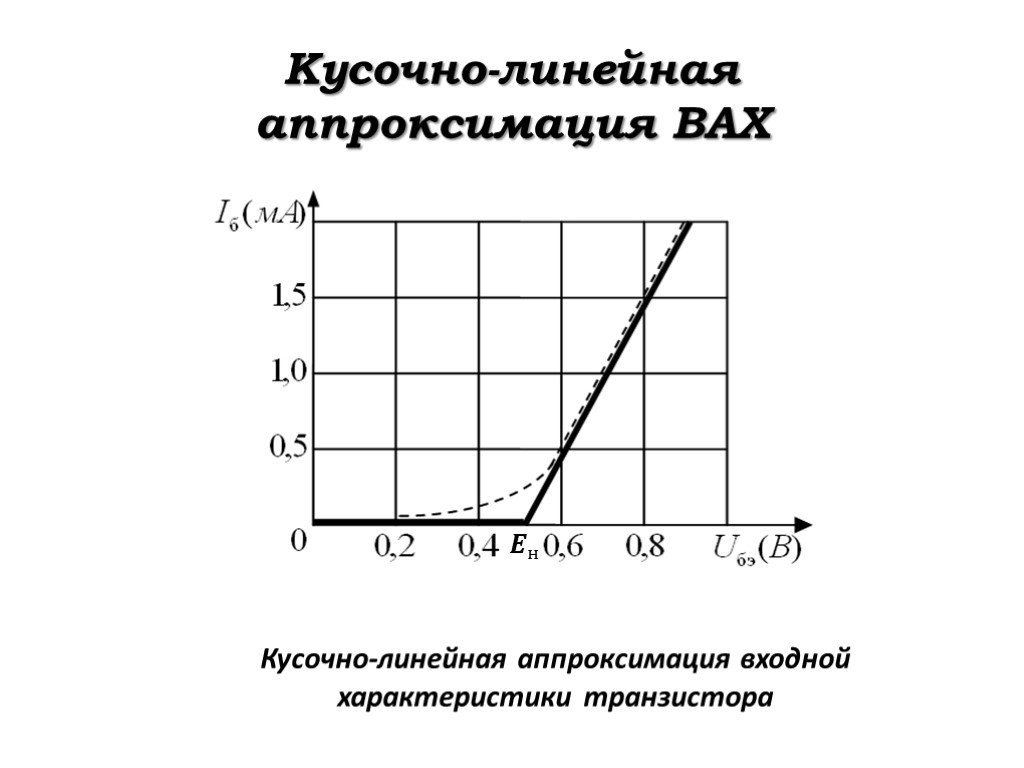
Слайд 17? н
Кусочно-линейная аппроксимация входной характеристики транзистора
Слайд 18Кусочно-линейная аппроксимация входной ВАХ транзистора
В общем случае дифференциальная крутизна характеристики в рабочей точке определяется отношением приращения тока к приращению напряжения, и при малых их значениях имеем
?= ∆? ∆? = ?? ??
............. (4)
Крутизна вольт-амперной характеристики ? измеряется в м? ? .
Уравнение отрезка прямой при кусочно-линейной аппроксимации характеристики записывается в виде
?= ? при ?< ? н ? ?− ? н при ?≥ ? н
.......... (5)
Чаще всего характеристику нелинейного элемента, к которому под-водится сигнал большой амплитуды, удаётся с приемлемой точно-стью аппроксимировать всего двумя отрезками прямых линий.
где ? н − напряжение начала входной ВАХ транзистора.

Слайд 19Расчёт кусочно-линейной аппроксимации входной ВАХ транзистора
Пример. Экспериментально снятая входная характеристика ? б =?( ? бэ )транзистора КТ601А представлена на слайде штриховой линией. Выполнить кусочно-линейную аппроксимацию данной характеристики в окрестности рабочей точки ? ? =?,? ?.
Решение.В соответствии с заданной ВАХ транзистора находим, что величина тока базы в рабочей точке ? ? =?,? м?. Крутизну характеристики в рабочей точке вычислим приближённо по формуле (4). Задав линейное приращение напряжения ∆? бэ =?,?−?,?=?,? ?, находим приращение тока базы:
∆? б =?,?−?,?=?м?
Тогда крутизна ВАХ определится как
?= ∆? б ∆? бэ = ? ?,?=? м? ?
Слайд 20В результате проведенной аппроксимации характеристики ток базы транзистора в окрестности рабочей точки с координатами ? ? =?,? ?, ? ? =?,? м? определится как:
? б = ? б? +? ? бэ − ? ?
Подставив значения величин ? б? = ? ? =?,? м? , ?=? м? ?
и ? ? =?,? ?, получим:
? б =?,?+? ? бэ −?,? =?( ? бэ −?,?)
Из этой формулы следует, что при ? бэ
Слайд 21Если же входное напряжение будет ? бэ
?= ? при ? бэ
Повышение точности аппроксимации характеристик нелинейных элементов достигается увеличением количества отрезков линий. Однако это усложняет аналитическое выражение аппроксимирую-щей функции.
Слайд 22Отклик нелинейной цепи на гармонический входной сигнал
Проанализируем физические процессы, протекающие в нелинейной цепи (рис.3), при воздействии на вход безынерци-онногонелинейного элемента ? гармонического сигнала ? ? ? = ? ? ????? и постоянного напряжения смещения ? ? .
Рис.3. Схема цепи с нелинейным элементом
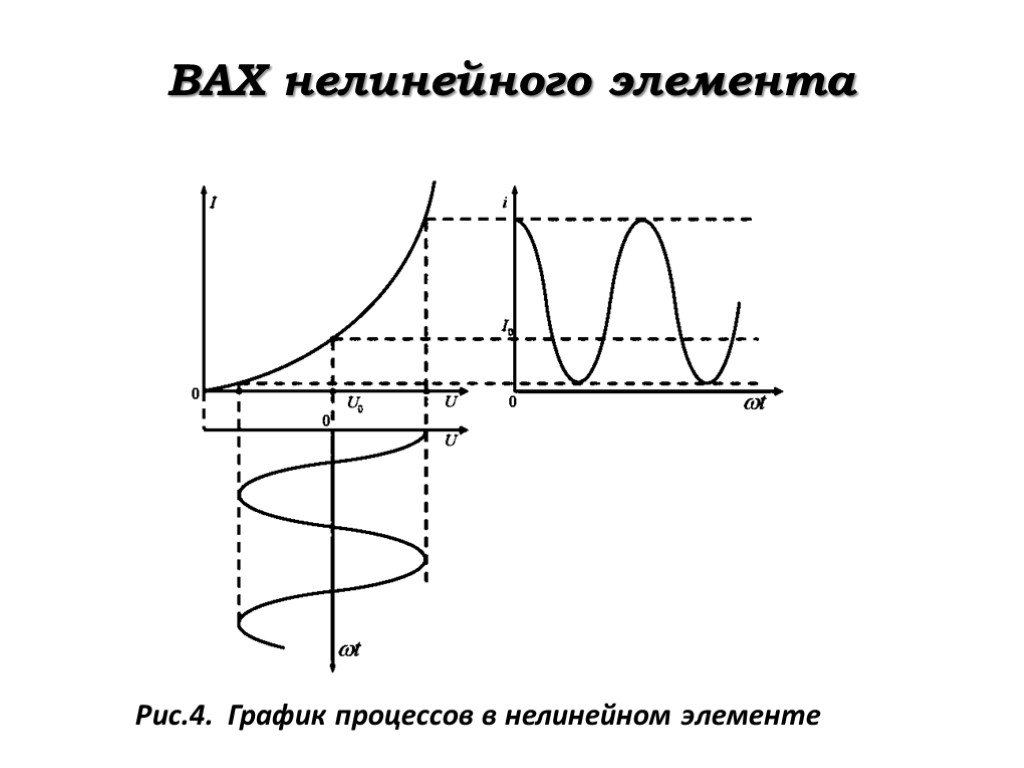
Слайд 23ВАХ нелинейного элемента
Рис.4. График процессов в нелинейном элементе
Слайд 24Отклик нелинейной цепи на входной гармонический сигнал
Вследствие нелинейности характеристики форма тока на выходе становится несинусоидальной. Причину этого искажения гармони-ческого колебания можно пояснить следующим образом.
Так как ток и напряжение связаны линейной зависимостью ∆?=?∆?, а крутизна ВАХ на разных участках неодинаковая (имеет нелинейный характер), то равным приращениям напряжения соответствуют неравные приращения тока.
Поскольку функция тока обладает периодичностью, то её можно представить тригонометрическим рядом Фурье:
? ? = ? ? + ?=? ∞ ? ? ??????
................. (6)
Здесь ? ?, ? ? , – амплитуды постоянной и гармонических составляющих.

Слайд 25Спектр тока в цепи с НЭ при степеннόйаппроксимации его характеристики
Пусть суммарное напряжение источников смещения и входного гармонического сигнала
? ? = ? ? + ? ? ?????
................ (7)
приложено к нелинейному элементу, ВАХ которого в окрестности рабочей точки аппроксимирована полиномом Тейлора вида:
? ? = ? ? + ? ? ?− ? ? + ? ? ?− ? ? 2+ ? ? ?− ? ? 3
+… ....... (8)
Подставив формулу (7) в выражение (8), получим:
? ? = ? ? + ? ? ? ? ?????+ ? ? ? ? ? ??? ? ??+ ? ? ? ? ? ??? ? ??+
.....
Слайд 26Спектр тока в цепи с НЭ пристепеннόйаппроксимации его характеристики
Используя известные формулы разложения степеней косинусов, получим:
??? ? ?= ? ? ?+?????
??? ? ?= ? ? (?????+?????)
??? ? ?= ? ? (?+??????+?????)
Выполнив подстановки и упростив выражения, запишем общее выражение для тока нелинейной цепи в компактной форме:
? ? = ? ? + ? ? ?????+ ? ? ??????+ ? ? ??????+ …
..... (9)
Слайд 27Здесь постоянная составляющая и амплитуды гармоник тока:
? ? = ? ? + ? ? ? ? ? ? ? + ? ? ? ? ? ? ? +
? ? = ? ? ? ? + ? ? ? ? ? ? ? + ? ? ? ? ? ? ? + .....
? ? = ? ? ? ? ? ? ? + ? ? ? ? ? ? ? + .....
? ? = ? ? ? ? ? ? ? + ? ?? ? ? ? ? ? + .....
......... (10)
Анализ состава формул (10) показывает, что при степеннόй аппро-ксимации характеристики гармонический состав тока в цепи с НЭ существенно зависит от степени полинома. При этом постоянная составляющая и амплитуды чётных гармоник определяются чёт-ными, а амплитуды нечётных гармоник – нечётными коэффици-ентамистепеннόго полинома.

Слайд 28Спектр тока в цепи с НЭ при кусочно-линейной аппроксимации его характеристики
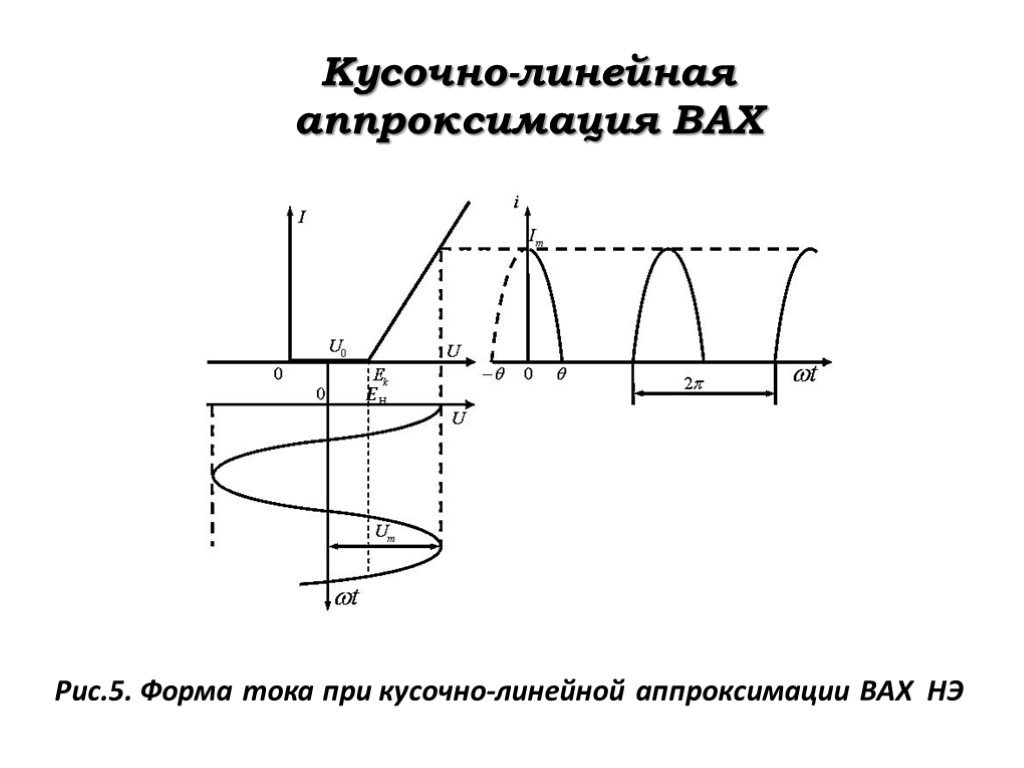
Пусть суммарное гармоническое и постоянное напряжение вида (7) подаётся на вход электрической цепи с НЭ, характеристика которого аппроксимирована кусочно-линейной линией и описывается формулой (5). В этом случае временнáя диаграмма тока, протекающего через нелинейные цепи, имеет форму косинусоидальных импульсов с отсечкой их нижней части (рис.5).
Слайд 29Рис.5. Форма тока при кусочно-линейной аппроксимации ВАХ НЭ
Слайд 30Параметр ?(в радианах или градусах), при котором ток изменяется от максимального значения ? ? до нуля, называется углом отсечки тока.
(Другое определение этого параметра: угол, соответствующий половине той части периода, в течение которой в выходной цепи нелинейного элемента протекает ток, называется углом отсечки и обозначается буквой ).
Изменение фазы, соответствующее длительности полного импульса на выходе цепи, равно ??. Из графиков предыдущего слайда можно определить, что при фазовом угле ??=?напряжение начала характеристики ? Н = ? ? + ? ? ????, откуда
????= ( ? Н − ? ? ) ? ?
.......... (11)

Слайд 31Подставив в формулу (5) суммарное напряжение источников сигнала и смещения из выражения (7) и напряжение начала характеристики ? Н получим аналитическую запись формы тока в зависимости от фазового угла:
? ?? =? ? ? (?????− ????)
при условии −?≤??≤?
...... (12)
Полученную чётную функцию ? ?? периодической последователь-ностиимпульсов тока (12) можно разложить в тригонометри-ческийряд Фурье (8), в котором период повторения составляет ??, длительность импульса - ??, а текущей переменной является мгновенный фазовый угол ?=??.

Слайд 32В этих импульсах тока постоянная составляющая запишется следующим образом:
? ? = ? ? ? ?? − ? ? (?????− ????)???= ? ? ? ? (????−?????)
..... (13)
Амплитуда первой гармоники:
? ? = ? ? ? ?? − ? ? (?????− ????)????????= ? ? ? ? (?−????????)
.... (14)
Подобным же образом определяются амплитуды гармонических составляющих ? ? и для ?=?,?, .... . При этом обобщённая формула для вычисления этих гармоник будет:
? ? = ?? ? ? ? ?????????−?????????? ?( ? ? −?)
........... (15)
Слайд 33Функции (коэффициенты) Берга
В радиотехнике полученные результаты записываются в специальной форме:
? ? =? ? ? ? ?
? ? =? ? ? ? ?
? ? =? ? ? ? ?
........... ....... (16)
Здесь ? ? , ? ? , ...... , ? ? – так называемые функции (коэффициенты) Берга, или коэффициенты гармоник, отражающие величины присутствующих гармоник в спектре преобразованного тока, которые аналитически записываются следующим образом:
Слайд 34? ? = ? ? (????−?????)
? ? = ? ? (?−????????)
? ? = ? ? ?????????−?????????? ?( ? ? −?)
............ (17) где ?=?,?,......
Коэффициенты гармоник очень часто используются в инженер-ных расчётах, например, при проектировании схем нелинейных уси-лителей мощности, умножителей частоты и автогенераторов. Поэтому они приводятся в специальной литературе.

Слайд 35Расчёт коэффициентов Берга
Пример.Характеристика нелинейного элемента имеет кусочно-линейную аппроксимацию двумя отрезками, у которой ? Н =?,? ?, ?=?,??м?/?. На элемент воздействует суммарное (постоянное и переменное) напряжение ? ? =?.?+?,?????? ?. Определить постоянную составляющую и первую гармонику тока, протекаю-щихчерез нелинейный элемент цепи.
Решение. Воспользовавшись формулой (11), находим, что ????= ?,?−?,? ?,? =?,?. Отсюда угол отсечки тока, протекающего через нелинейный элемент, ?=??°. Два первых коэффициента гармоник, соответствующих этому углу, будут: ? ? =?,??; ? ? =?,?. Подставив последовательно эти значения в соотношение (16), вычисляем соответственно амплитуды постоянной составляющей и первой гармоники: ? ? =?м?, ? ? =?м?.

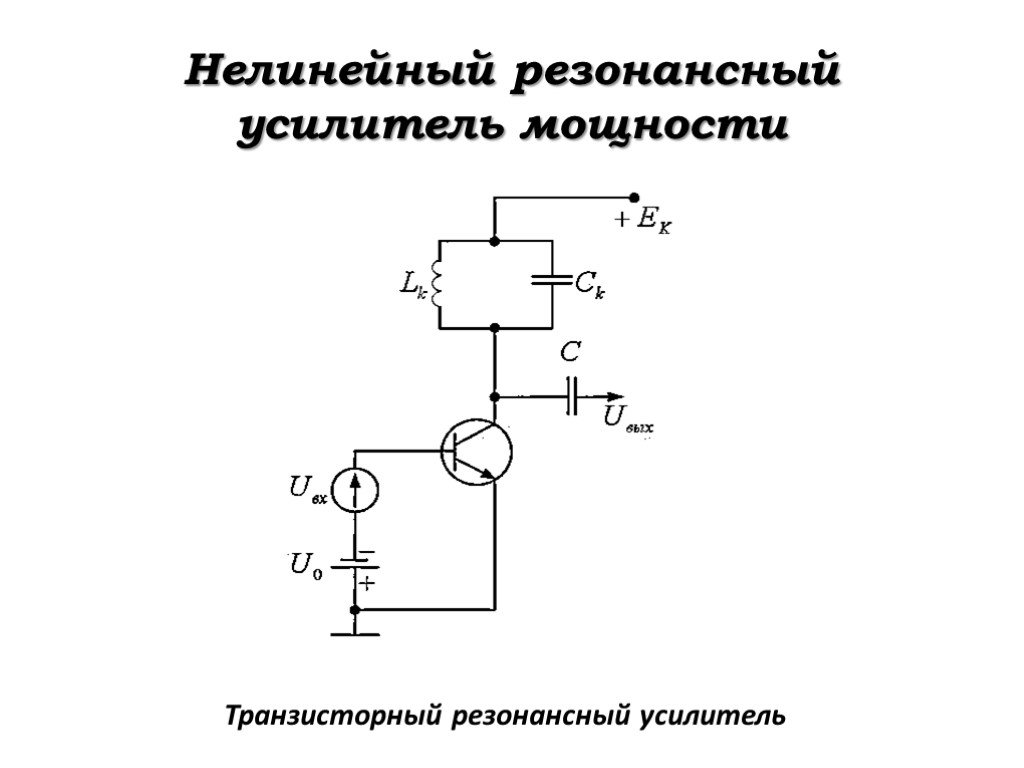
Слайд 36Нелинейный резонансный усилитель мощности
В радиопередающих устройствах широкое применение находят резонансные усилители мощности и умножители частоты.
Пусть к входу нелинейного резонансного усилителя мощности на транзисторе последовательно подключены источники гармоничес-кого напряжения ? вх ? = ? ? вх ??? ? р ?и постоянного напряжения смещения ? ? , а резонансный контур нагрузки настроен на частоту усиливаемого сигнала ? р .
Слайд 37Транзисторный резонансный усилитель
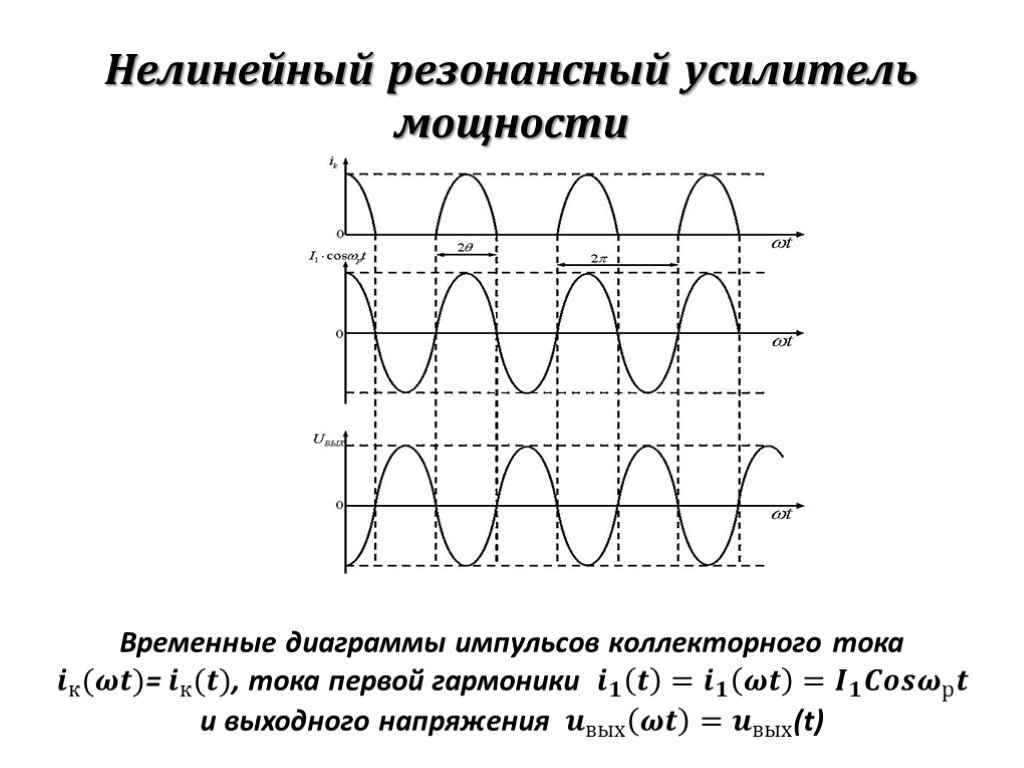
Слайд 38Положим, что коллекторный ток транзистора имеет форму косинусоидальных импульсов с отсечкой. Временные диаграммы импульсов коллекторного тока ? к (??)= ? к (?), тока первой гармо-ники ? ? ? = ? ? ?? = ? ? ??? ? р ?и выходного напряжения ? вых ?? = ? вых ? показаны на следующем слайде.
Слайд 39Временные диаграммы импульсов коллекторного тока ? к (??)= ? к (?), тока первой гармоники ? ? ? = ? ? ?? = ? ? ??? ? р ? и выходного напряжения ? вых ?? = ? вых (t)
Слайд 40Спектральный состав косинусоидальных импульсов коллектор-ного тока содержит множество составляющих кратных частот, однако наибольшую амплитуду имеет первая гармоника. Это объясняется тем, что на резонансной частоте активное сопротив-ление параллельного контура максимально и поэтому на нём выде-ляется усиливаемое напряжение с частотой входного сигнала ? р . Сопротивление же параллельного контура на частотах ?? р , ?? р , ... столь мало, что высшие гармонические составляющие практически не дают вклада в формирование выходного сигнала ? вых ? .
Используя формулу (16) для коэффициентов Берга, запишем выра-жение для амплитуды выходного напряжения
? ? вых = ? ? ? ? =? ? ? вх ? ? ? ? ,
где ? ? – резонансное сопротивление параллельного контура; коэффициент Берга для первой гармоники.
................... (18) ? ? –

Слайд 41Умножитель частоты
Умножитель частоты – это устройство, повышающее частоту входного сигнала в ? раз, где ? – целое число – коэффициент умножения.
Необходимость в умножителях частоты возникает при разра-ботке высокостабильных источников гармонических колебаний повышенной частоты, когда непосредственное генерирование сиг-налов такого диапазона затруднительно.
Наличие в спектре коллекторного тока гармонических составля-ющих с частотами, кратными входной частоте, позволяют использовать нелинейный резонансный усилитель в качестве умножителя частоты.

Слайд 42Для этого достаточно в схеме резонансного усилителя настро-итьколебательный контур на требуемую частоту. Известно, что при больших значениях ? коэффициенты гармоник ? ? довольно малы, поэтому важно выбрать такой угол отсечки коллекторного тока ?, при котором соответствующие коэффициенты гармоник максимальны.
Практически доказано, что оптимальный угол отсечки, дающий наибольшую амплитуду выходного напряжения в умножителях частоты, примерно равен ???° ? .
Слайд 43Принципы действия умножителя частоты и нелинейного резонансного усилителя мощности в основном одинаковы и различия заключаются лишь в выборе угла отсечки тока. По аналогии с выражением (18) определим амплитуду выходного напряжения умножителя частоты при кусочно-линейной аппроксимации характеристики транзистора
? ?? = ? ? ? ?? =? ? ? вх ? ? ? ?? ,
.......... (19)
где ? ?? – резонансное сопротивление контура на ? - й гармонике; ? ? – коэффициент Берга для ? - й гармоники.















































![Вольт-амперная характеристика нелинейного устройства. Нелинейные цепи характеризуются сложной зависимостью между входным сигналом ? вх (?) и выходной реакцией ? вых ? , которую в общем виде можно записать так: ? вых ? =?[ ? вх (?)]. В нелинейных цепях с безынерционными НЭ в качестве воздейст-вия наи Вольт-амперная характеристика нелинейного устройства. Нелинейные цепи характеризуются сложной зависимостью между входным сигналом ? вх (?) и выходной реакцией ? вых ? , которую в общем виде можно записать так: ? вых ? =?[ ? вх (?)]. В нелинейных цепях с безынерционными НЭ в качестве воздейст-вия наи](https://prezentacii.org/upload/cloud/19/09/165095/images/thumbs/screen10.jpg)















































