Презентация "НЕЛИНЕЙНЫЕ РЕЗИСТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ" – проект, доклад

НЕЛИНЕЙНЫЕ РЕЗИСТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

Вольт – амперные характеристики нелинейных резистивных элементов (ВАХ)

Для нелинейного резистивного элемента характерна нелинейная зависимость между током и напряжением i=f(u) . Эта зависимость может быть задана в графическом, табличном или аналитическом виде. На рисунке показано схемное обозначение нелинейного резистивного двухполюсного элемента.

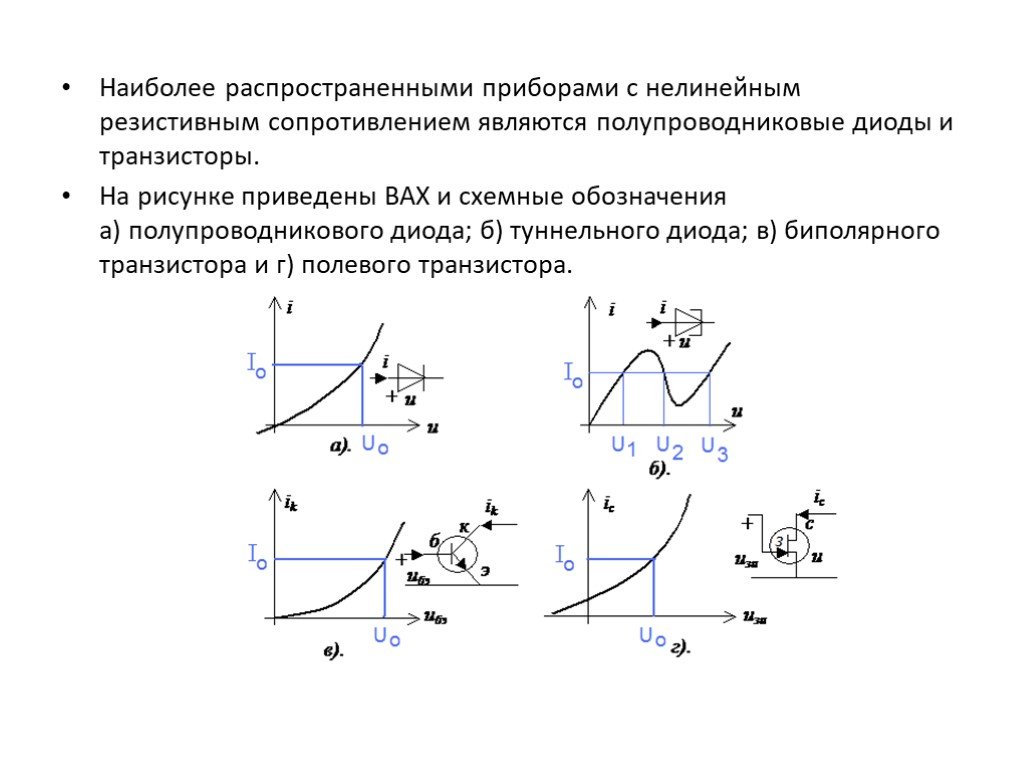
Наиболее распространенными приборами с нелинейным резистивным сопротивлением являются полупроводниковые диоды и транзисторы. На рисунке приведены ВАХ и схемные обозначения а) полупроводникового диода; б) туннельного диода; в) биполярного транзистора и г) полевого транзистора.

ВАХ делятся на однозначные, когда одному значению напряжения соответствует одно значение напряжения (характеристики а, в и г ), и многозначные, когда одному значению тока или напряжения соответствует несколько значений напряжения или тока (характеристика б). Аппроксимация вольт – амперных характеристик Как правило, ВАХ нелинейных элементов получают экспериментально, поэтому они задаются в виде таблиц или графиков. При анализе удобно иметь дело с аналитическими выражениями. Аппроксимация – это замена графической кривой подходящим аналитическим выражением.

Аппроксимация степенным полиномом. Этот вид аппроксимации используется для аналитического представления ВАХ в окрестности рабочей точки (i=IР, u=UР). При этом аналитическое выражение имеет структуру ряда Тейлора: i=a0+a1(u-UР)+a2(u-UР)2+a3(u-UР)3+……+an(u-UР)n. В процессе решения задачи аппроксимации определяются коэффициенты a0, a1,…, an полинома наиболее просто методом интерполяции из условия равенства значений полинома и аппроксимируемой ВАХ в выбранных точках (узлах интерполяции).

Кусочно - линейная аппроксимация. Если к НЭ приложено гармоническое напряжение с большой амплитудой, то для аппроксимации ВАХ целесообразно использовать отрезки прямых линий. Можно считать, что эта характеристика имеет два участка: первый – там, где ток близок к нулю и он заменяется линией i=0 при u  Uотс; второй – там, где ток растет с ростом напряжения и он заменяется линией i=S(u-Uотс) при u >Uотс, где S – крутизна характеристики, а Uотс – напряжение отсечки (эти параметры определяют по заданной в виде таблицы или графика ВАХ).

Режим постоянного тока в цепи с одним нелинейным элементом. Определение рабочей точки

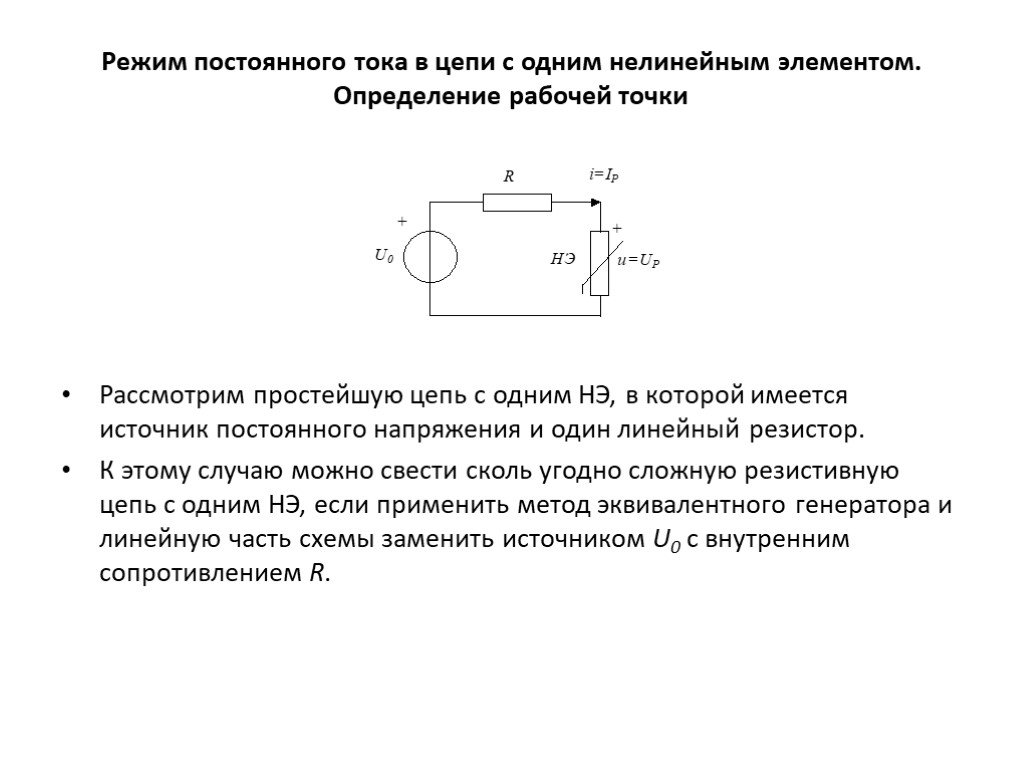
Рассмотрим простейшую цепь с одним НЭ, в которой имеется источник постоянного напряжения и один линейный резистор. К этому случаю можно свести сколь угодно сложную резистивную цепь с одним НЭ, если применить метод эквивалентного генератора и линейную часть схемы заменить источником U0 с внутренним сопротивлением R.

Необходимо определить напряжение UР и ток IР через НЭ, или рабочую точку на ВАХ нелинейного элемента. Запишем уравнение Кирхгофа для данной схемы: откуда получим выражение для тока Ток через нелинейный элемент, то он должен одновременно удовлетворять уравнению для ВАХ i=f(u). Тогда

Построим графики двух этих функций, и точка пересечения графиков будет рабочей точкой, т.е. решением рассматриваемой системы. Первая кривая является прямой линией в координатах u-i, вторая задана.

Отметим, что режим постоянного тока в цепи с нелинейным элементом является вспомогательным и служит для обеспечения рабочей точки на ВАХ нелинейного элемента.

Статические и дифференциальные параметры нелинейных элементов

Для резистивных НЭ важным параметром является их сопротивление, которое в отличие от линейных резисторов не является постоянным, а зависит от того, в какой точке ВАХ оно определяется. Различают два вида сопротивлений : статическое и дифференциальное. Статическое сопротивление определяется как - напряжение и ток в рабочей точке. - сопротивление постоянному току, оно характеризуется тангенсом угла наклона прямой, проходящей через начало координат и рабочую точку.

Статические характеристики определяют отношения между мгновенными значениями напряжения и тока на внешних зажимах нелинейного элемента. Дифференциальное сопротивление Введем понятие дифференциальной проводимости, которая является величиной, обратной . Эта величина которой может быть определена из соотношения: Gдиф=1 / Rдиф= где U0 - напряжение рабочей точки. Дифференциальное сопротивление является сопротивлением НЭ переменному току малой амплитуды. Оно может быть как положительным, так и отрицательным. Туннельный диод имеет падающий участок характеристики, и поэтому его называют прибором с отрицательным сопротивлением.

Анализ нелинейной электрической цепи при гармоническом воздействии

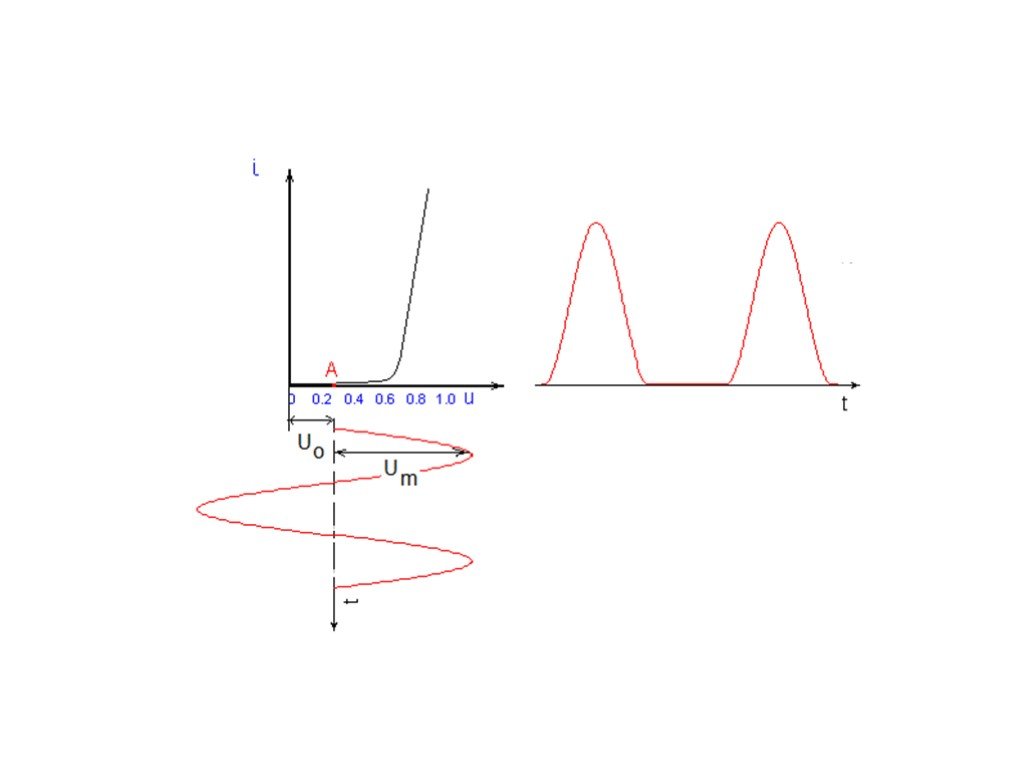
Пусть теперь на НЭ действует сумма постоянного и гармонического напряжений u(t)=U0+Umcos t. Для нахождения реакции НЭ на заданное воздействие можно найти графическим методом. Такой метод получил название метода трех плоскостей. По каждому мгновенному значению напряжения из плоскости «напряжение – время» через плоскость ВАХ i=f(u) определяется соответствующее мгновенное значение тока на плоскости «ток – время».

u(t)=U0+Umcos t

Режим малого сигнала

Пусть амплитуда Um переменной составляющей мала по сравнению с U0 . Поэтому небольшой участок ВАХ, который захватывается переменной составляющей приложенного напряжения можно считать линейным. Такой режим работы нелинейного элемента называется режимом малого сигнала.

В рассматриваемом режиме малого сигнала и рабочая точка будет смещаться за счёт переменой составляющей в переделах малого участка BAX, который по этой причине можно считать линейным.

Для аппроксимации этого участка BAX можно применить линейную аппроксимацию, т.е. аппроксимацию полиномом первой степени. = I0 +Sдиф (u-U0) - дифференциальная крутизна ВАХ в рабочей точке (т.е. при u=U0 ).

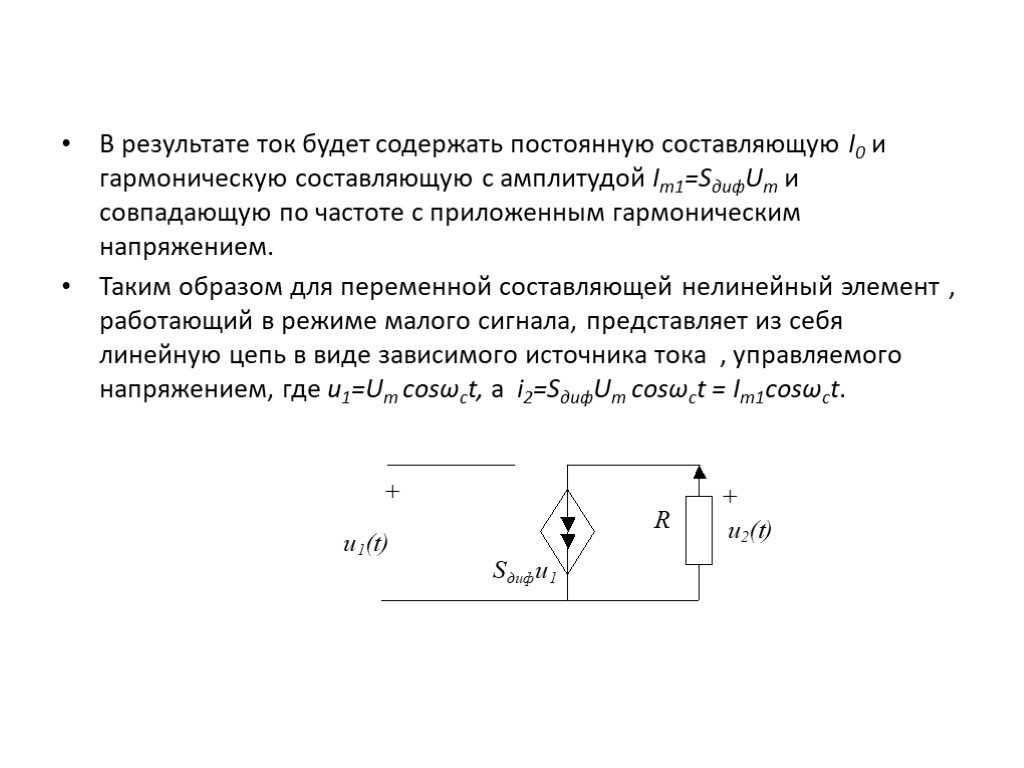
В результате ток будет содержать постоянную составляющую I0 и гармоническую составляющую с амплитудой Im1=SдифUm и совпадающую по частоте с приложенным гармоническим напряжением. Таким образом для переменной составляющей нелинейный элемент , работающий в режиме малого сигнала, представляет из себя линейную цепь в виде зависимого источника тока , управляемого напряжением, где u1=Um cosωct, а i2=SдифUm cosωct = Im1cosωct.

Режим большого сигнала

Предположим, что на входе нелинейного элемента действует напряжение: и что амплитуда переменной составляющей соизмерима с напряжением смещения . Тогда переменная составляющая будет смещать рабочую точку, захватывая значительную часть BAX, так что её уже нельзя представить линейной функцией.

Рассмотрим аппроксимацию рабочего участка BAX полиномом второй степени который содержит в дополнение к линейному ещё и квадратичный член, позволяющий аппроксимировать небольшие нелинейности BAX. Подставим в это выражение напряжение, изменяющееся по гармоническому закону:

Таким образом, при воздействии на нелинейный элемент постоянной составляющей и гармонического напряжения с частотой с в спектре реакции (тока) появляется вторая гармоника с частотой . Очевидно, что при более существенной нелинейности BAX необходимо при её аппроксимации использовать полином третьего или более высокого порядка, что приведёт к появлению в спектре тока высших гармоник. Это свидетельствует о том, что форма тока через нелинейный элемент при гармоническом воздействии будет отличаться от гармонической. Чтобы количественно оценить степень искажения сигнала на выходе усилителя вводят коэффициент нелинейных искажений: Он показывает среднеквадратический уровень всех высших гармоник относительно амплитуды первой гармоники тока.

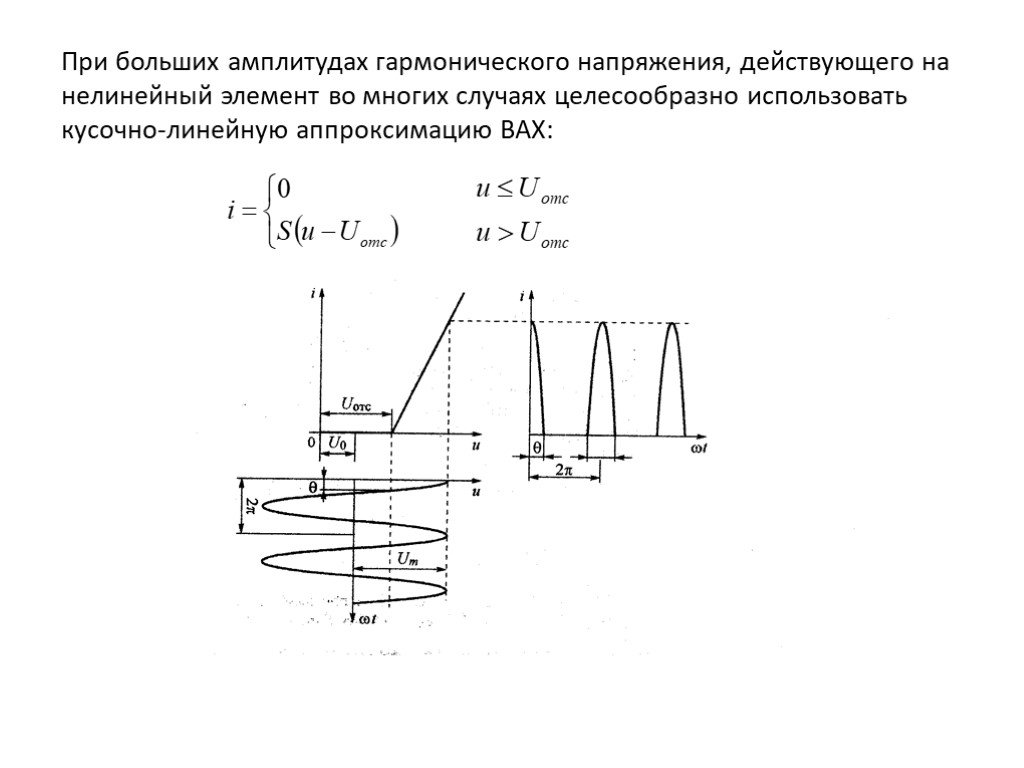
При больших амплитудах гармонического напряжения, действующего на нелинейный элемент во многих случаях целесообразно использовать кусочно-линейную аппроксимацию BAX:

При воздействующем напряжении по методу трёх плоскостей можно построить график тока , который имеет вид косинусоидальных импульсов с отсечкой. Ширина этих импульсов в угловых единицах (в радианах или градусах) составляет 2 , где  называется углом отсечки. Из графика рис. 6.10 можно вычислить угол отсечки . Очевидно, этот угол удовлетворяет равенству: При заданной аппроксимирующей функции угол отсечки можно менять за счёт напряжения смещения и амплитуды гармонического воздействия. Аналитическое выражение для импульсов тока можно найти после подстановки:

Здесь записано выражение для одного импульса тока. Этот импульс периодически повторяется с частотой и периодом Такую периодическую последовательность импульсов можно представить в виде ряда Фурье: Спектр амплитуд и спектр фаз определяются по известному аналитическому выражению. Опуская вычисления, приведём формулу для определения амплитуд гармоник: где называется функциями Берга

Они зависят от угла отсечки и их значения для разных углов отсечки приводятся в справочниках. Для примера на рисунке приведены графики нескольких функций Берга Функции Берга имеют максимальные значения при Таким образом, в нелинейной электрической цепи происходит обогащение спектра передаваемого сигнала. Реакция имеет спектральные составляющие, которых нет в воздействии.