Презентация "Теоремы об углах, образованных хордами, касательными и секущими" – проект, доклад
Презентацию на тему "Теоремы об углах, образованных хордами, касательными и секущими" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
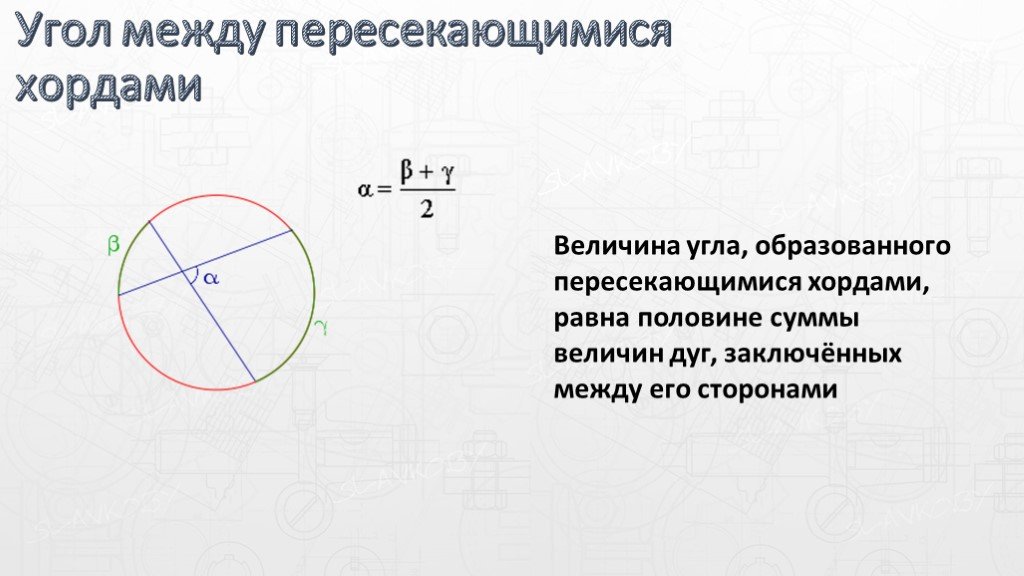
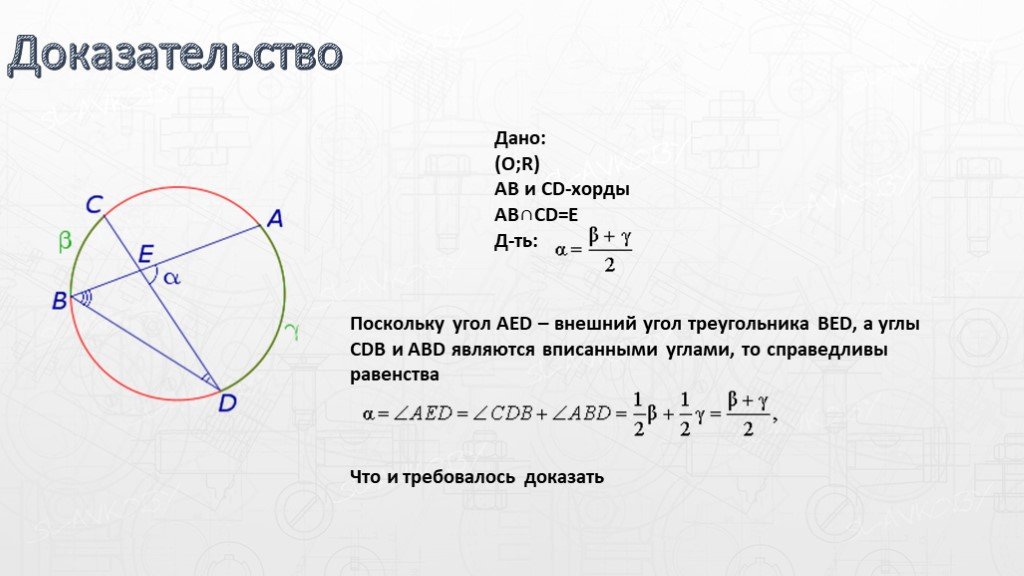
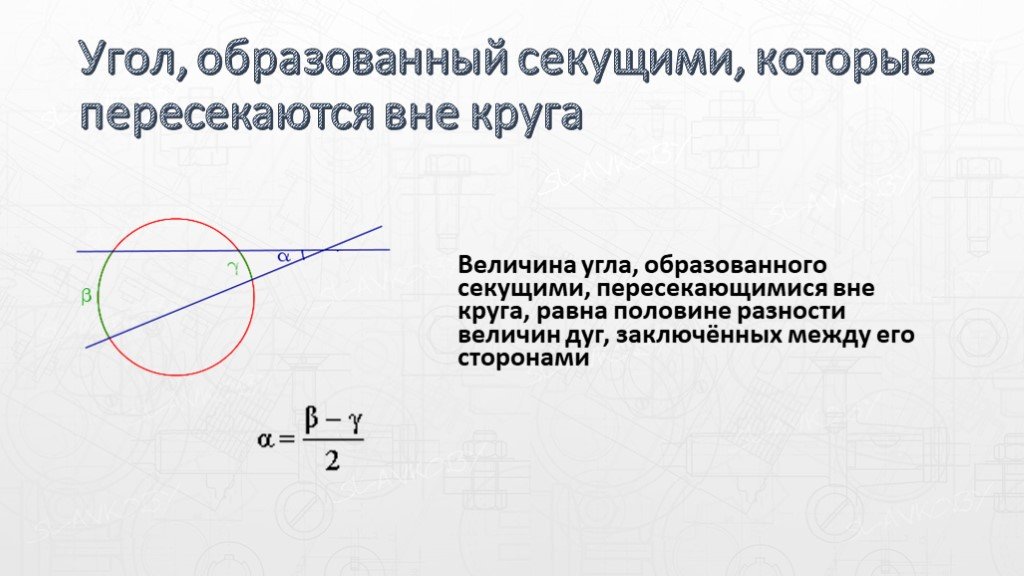
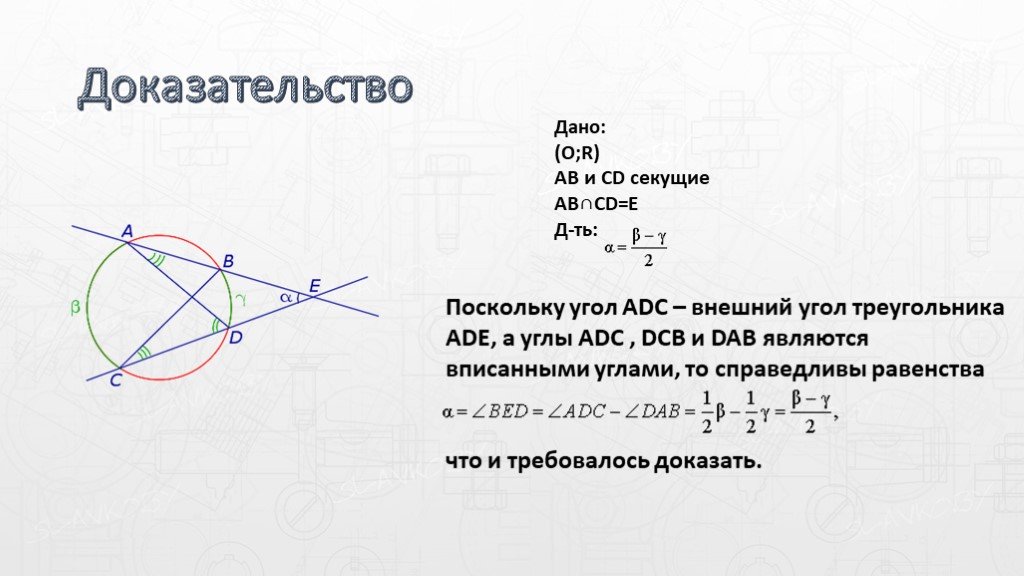
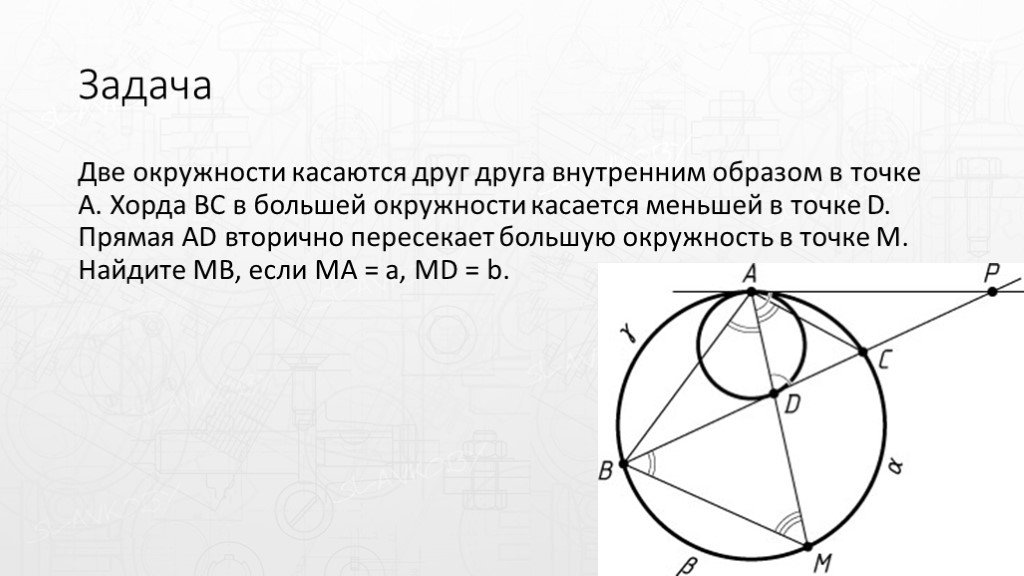
Слайды презентации
Список похожих презентаций
Интересные факты об Англии
1.Уйти по-английски, что это значит? Когда кто-то уходит, не прощаясь, мы употребляем выражение «ушёл по-английски». Появилась она в период Семилетней ...Еще раз об этикете
Этике́т (от фр. etiquette — этикетка, надпись) — нормы и правила, отражающие представления о должном поведении людей в обществе. В современном виде ...Все об инсульте
1. Понятие. Факторы риска возникновения инсульта. Инсульт (от лат. insulto - скачу, впрыгиваю) "апоплексический удар" или "мозговой удар" — представляет ...Всего лишь один миф об авторском праве в интернете
Преамбула. Dura lex sed lex! (Суров закон, но это закон!) Закон Республики Казахстан «Об авторском праве и смежных правах» от 10 июня 1996 г. № 6-1 ...Все об антикризисном управлении
Кризис. – это крайнее обострение противоречий в социально-экономической системе, угрожающее ее жизнестойкости в окружающей среде. Виды кризисов. 1) ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 апреля 2019
Категория:Разные
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию