Слайд 1Топологические изоляторы и смежные вопросы
Школа ИТЭФ - 2011 М.В.Фейгельман ИТФ им. Л.Д.Ландау
Слайд 2План лекций
Лекция 1 - Введение Что такое топологические изоляторы Известные экспериментальные объекты Эксперименты (ARPES, STM, электр.транспорт)
Лекция 2 - Кое-что о теории - Топологические свойства зонных диэлектриков - Общая классификация топологических фаз Связь с проблемами спиновой жидкости и px+ipy сверхпроводящего состояния Майорановские фермионы: как напасть на их след
Слайд 3Что такое топологич. изолятор - 1
Простейший пример: зонный диэлектрик (3-мерный или 2-мерный), образующий поверхностные проводящие состояния Обобщение: любая система со щелью в спектре в объёме, но безщелевыми состояниями на поверхности (например, сверхтекучий 3He-B)
Слайд 5
Слайд 6Гамильтониан поверхностных электронных состояний
H = v0(-i∂ - eA)σ + geffσB
зеемановский член
двумерный градиент вдоль поверхности
Щель в спектре пропорциональна geffBz
Слайд 7Сравним с графеном:
один «дираковский» фермион вместо 4-х в графене (там 2 долины и 2 проекции спина) Не работает теорема удвоения ! Псевдоспин из ур-ния Дирака – это «почти» реальный спин электрона (в графене – это индекс подрешеток, не связанный со спином) Поэтому магнитное поле ┴ поверхности открывает щель в спектре
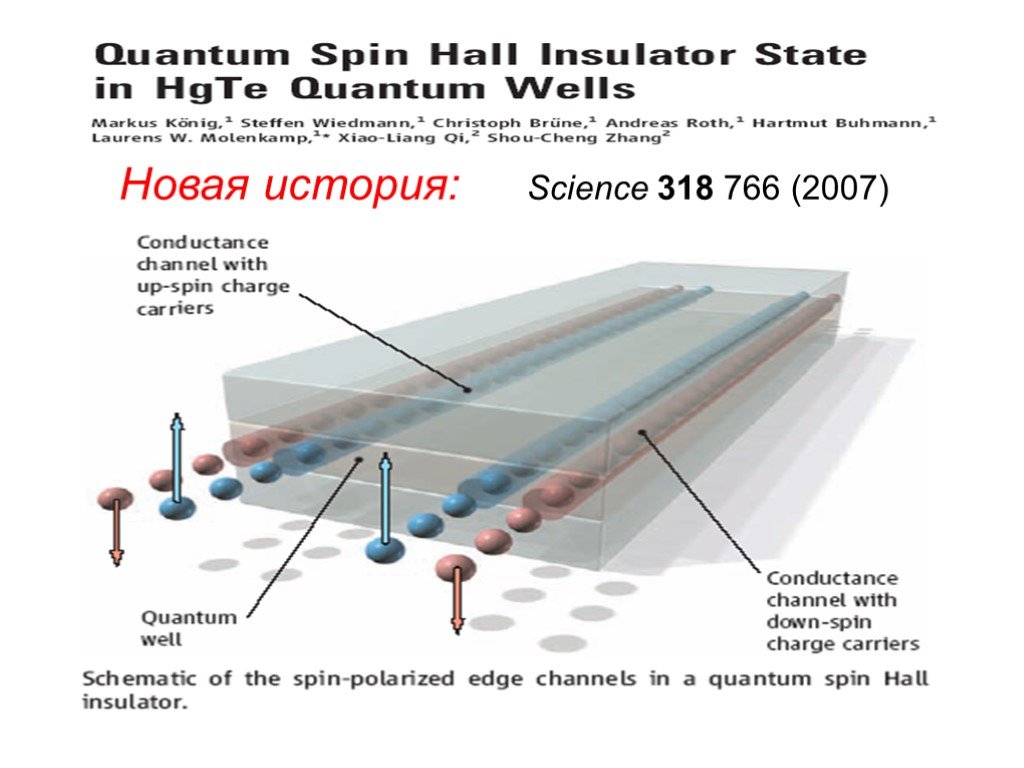
Слайд 8Новая история: Science 318 766 (2007)
Слайд 9Краевые состояния не имеют рассеяния назад
M < 0 leads to surface anomaly
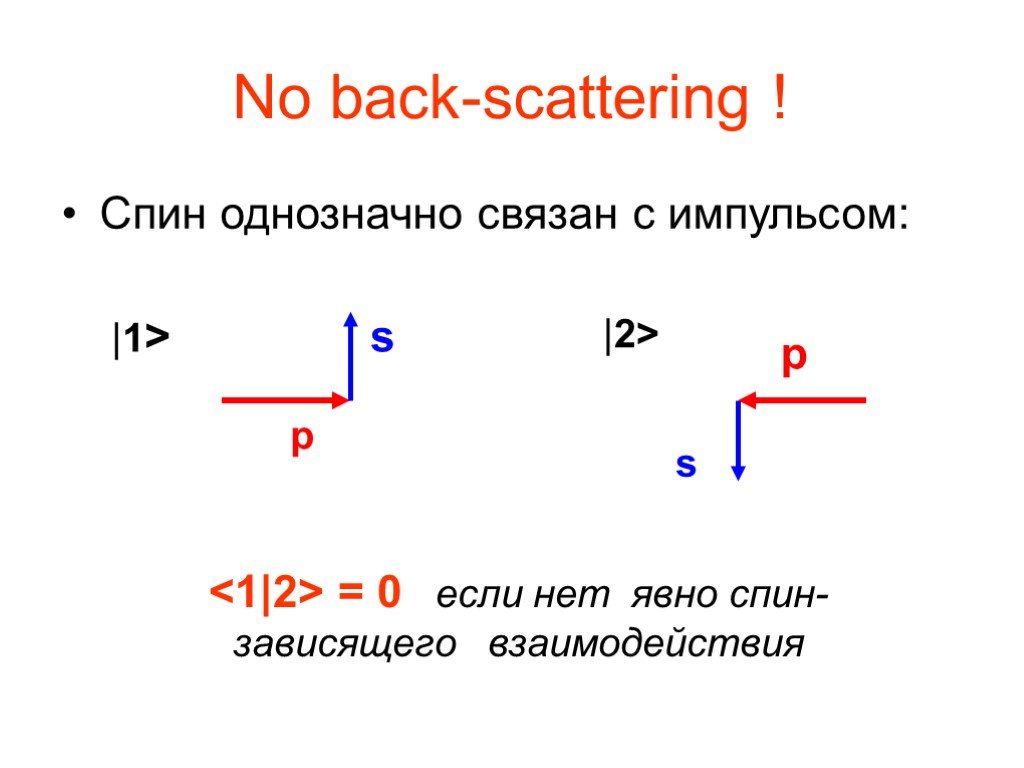
Слайд 10No back-scattering !
Спин однозначно связан с импульсом:
p s |1> |2>
<1|2> = 0 если нет явно спин-зависящего взаимодействия
Слайд 11Что такое топологич. изолятор - 2
Электродинамика с Ө-членом:
Ө = π (2n+1) для сохранения Т-инвариантности
exp(iS3D)= (-1)n
для интеграла по замкнутому пространству
(изложение по материалу M. Franz, Physics 1, 36 (2008)
Слайд 12Что будет при Ө ≠ CONST ?
топ. изолятор Ө=π
простой изолятор Ө=0
Аномальные члены сидят на границе Т-инвариантность там нарушена
Слайд 13Магнито-электрический эффект
Кроме того, эффект Керра – вращение плоскости поляризации отраженного света
Слайд 14“Dynamical Axion Field in Topological Magnetic Insulators” R. Li, J. Wang, X. Qi, S.-C. Zhang
Axions are very light, very weakly interacting particles postulated more than 30 years ago in the context of the Standard Model of particle physics. Their existence could explain the missing dark matter of the universe. However, despite intensive searches, they have yet to be detected. In this work, we show that magnetic fluctuations of topological insulators couple to the electromagnetic fields exactly like the axions, and propose several experiments to detect this dynamical axion field. In particular, we show that the axion coupling enables a nonlinear modulation of the electromagnetic field, leading to attenuated total reflection. We propose a novel optical modulators device based on this principle.
Arxiv: 0908.1537

Слайд 15Объекты, известные как Топологические Изоляторы или Топ. Сверхпроводники
2D: HgTe (квантовые ямы с 2D электронами) 3D: Bi1-xSbx Bi2Se3 Bi2Te3 Tl Bi Se2 3He-B Н.Копнин et al J.LowTemp.Phys. 85, 267 (1991) Г.Воловик Письма ЖЭТФ 90, 440 (2009). Topological superfluid 3He-B: fermion zero modes on interfaces and in the vortex core M.A. Silaev, G.E. Volovik arXiv:1005.4672
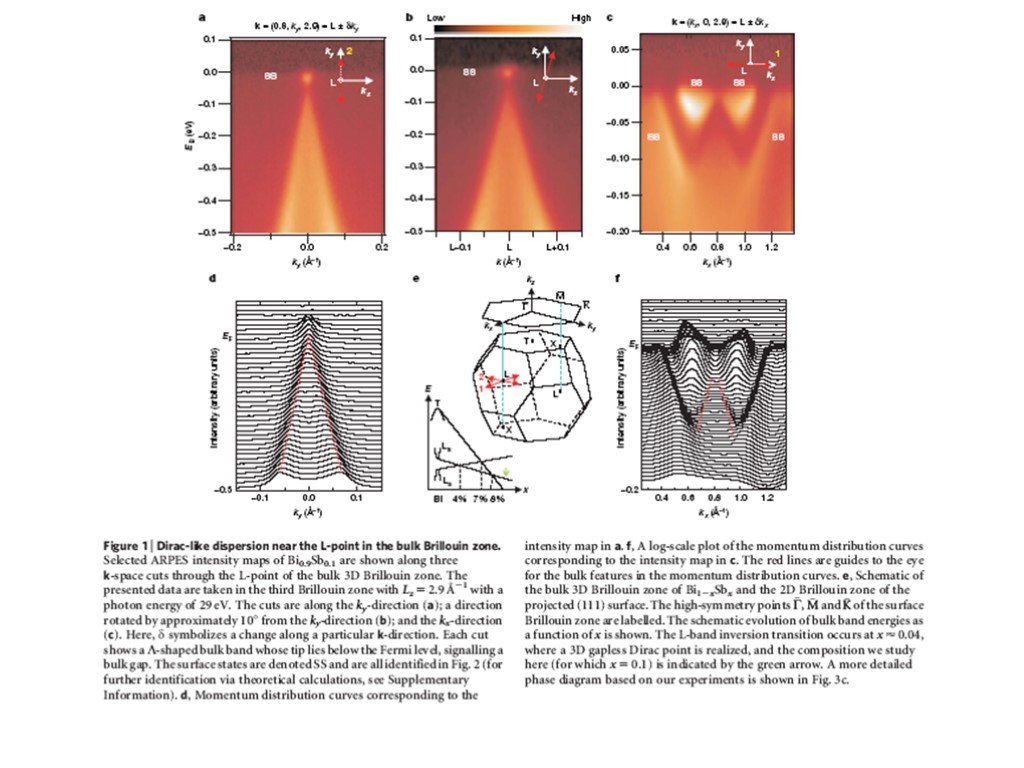
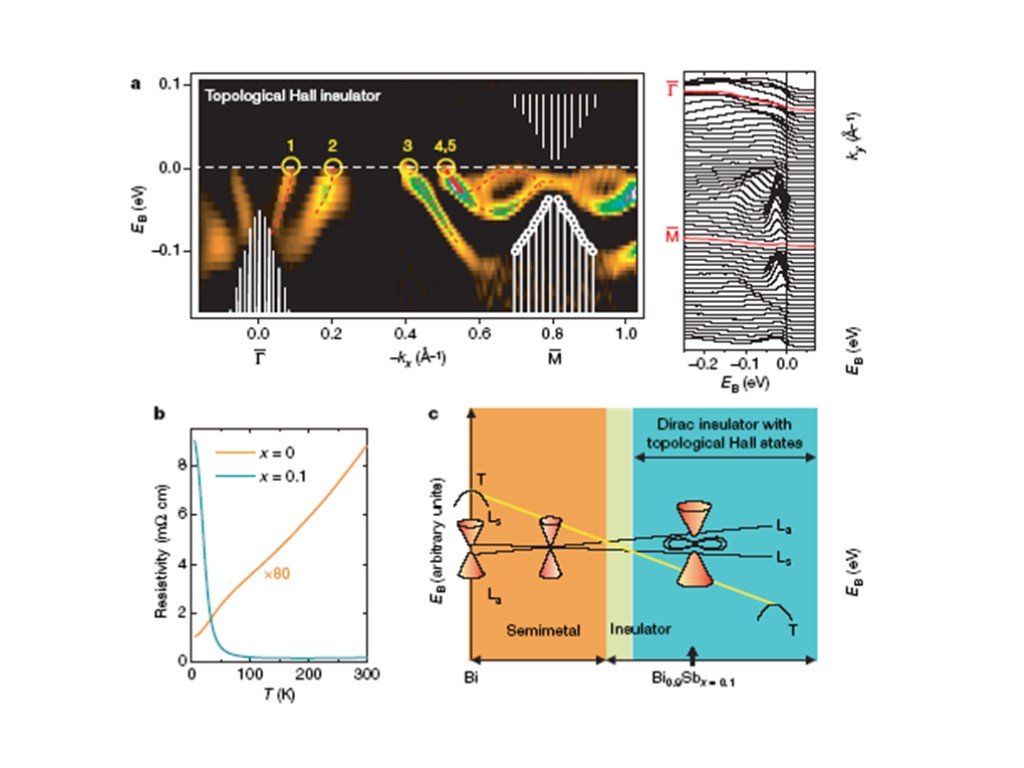
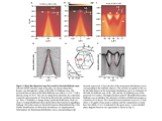
Слайд 16Эксперименты ARPES
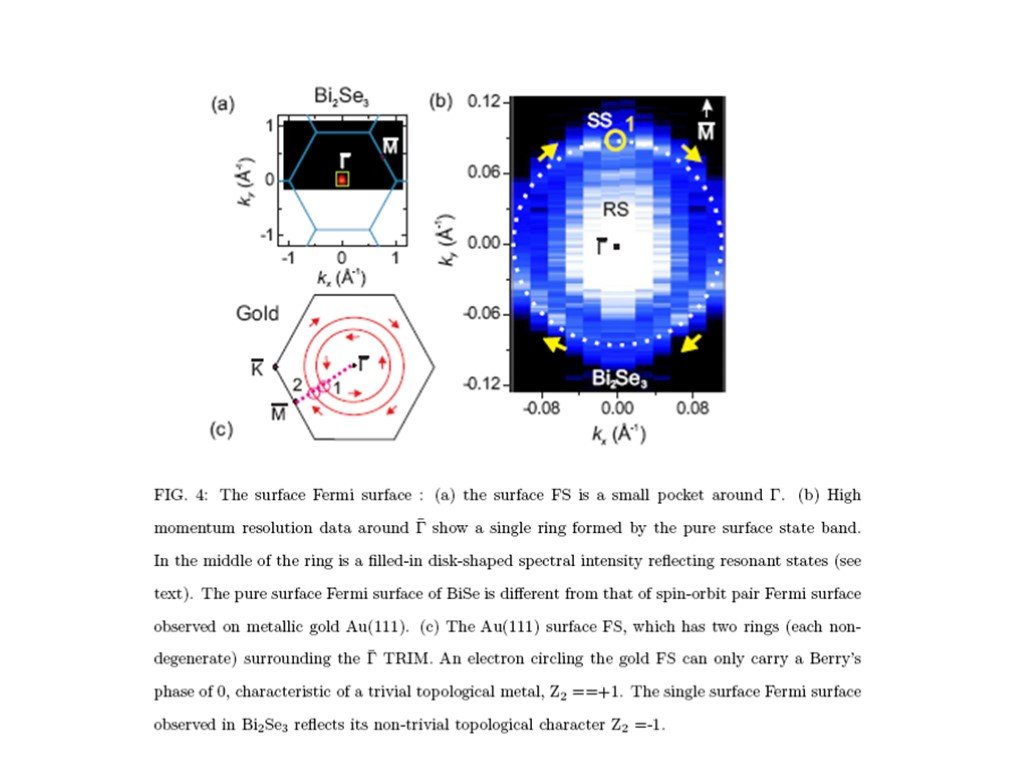
Слайд 17
Слайд 18
Слайд 20Band structure calculation
Слайд 21
Слайд 22Large Gap Topological Insulator Bi2Te3 with a Single Dirac Cone on the Surface Y. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. Fisher, Z. Hussain, Z. X. Shen arXiv:0904.1829
Слайд 23
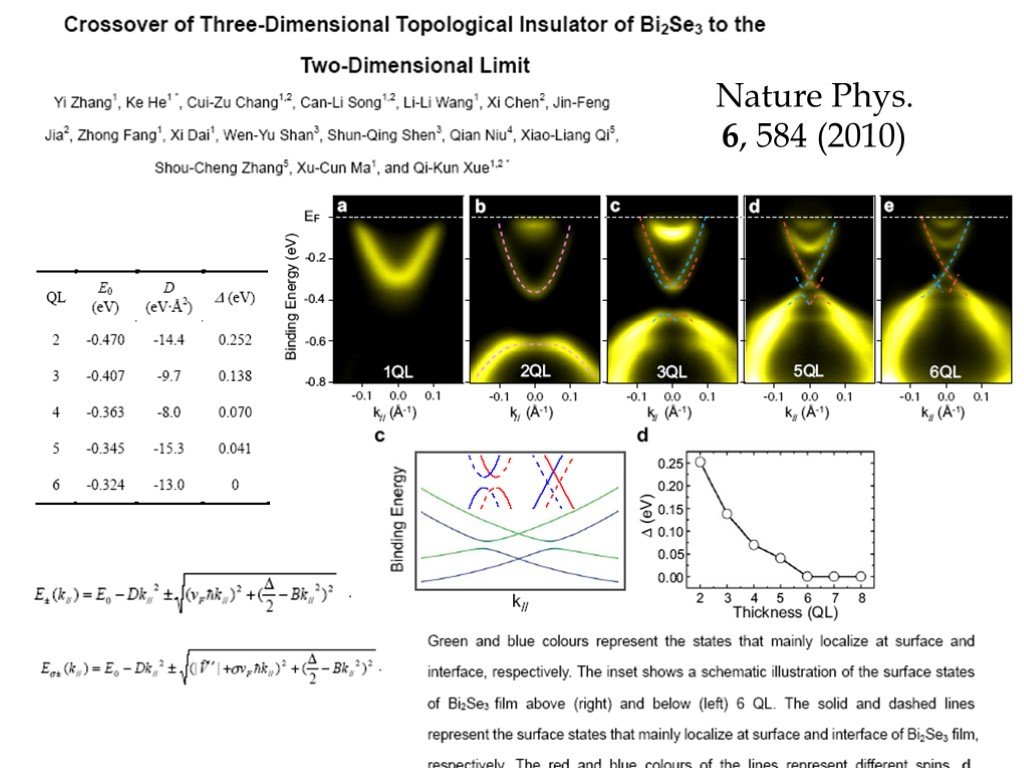
Слайд 24Nature Phys. 6, 584 (2010)
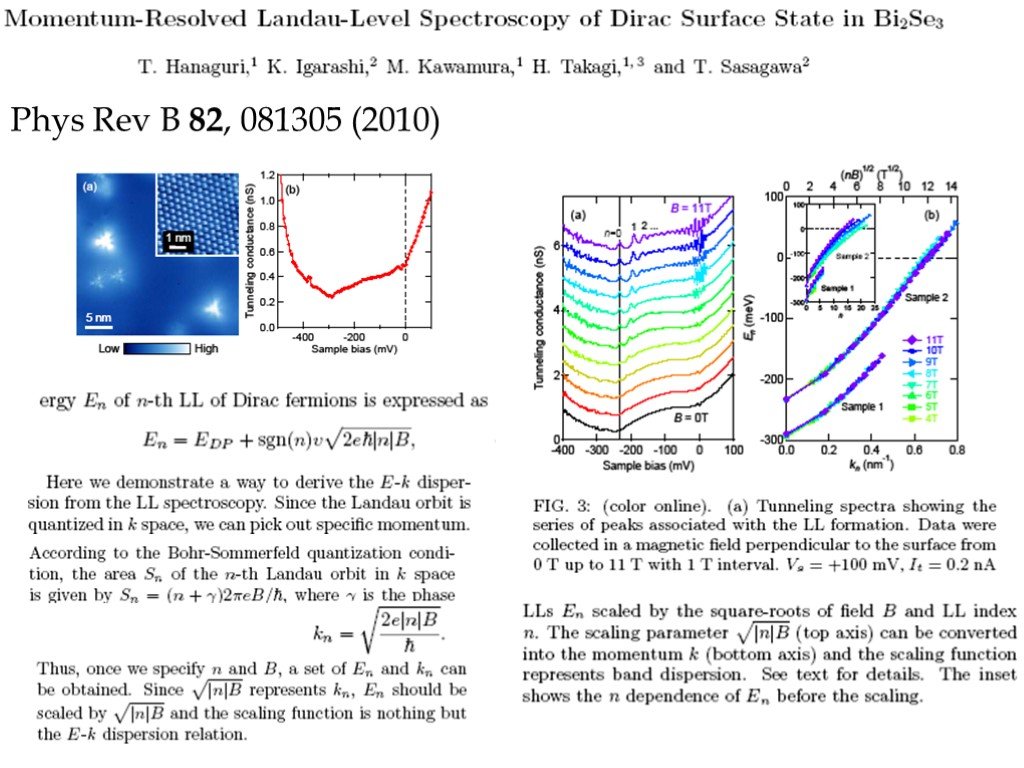
Слайд 25Phys Rev B 82, 081305 (2010)
Слайд 26Транспортные эксперименты
Aharonov-Bohm interference in topological insulator nanoribbons Hailin Peng, Keji Lai, Desheng Kong, Stefan Meister, Yulin Chen, Xiao-Liang Qi, Shou-Cheng Zhang, Zhi-Xun Shen, Yi Cui arXiv:0908.3314
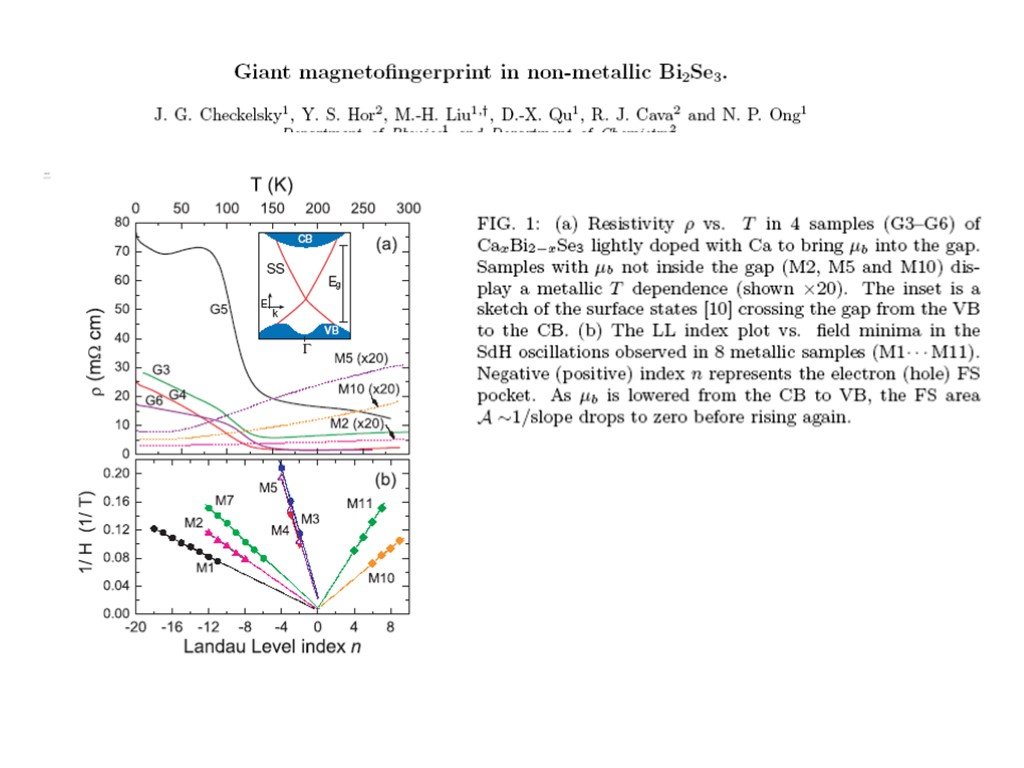
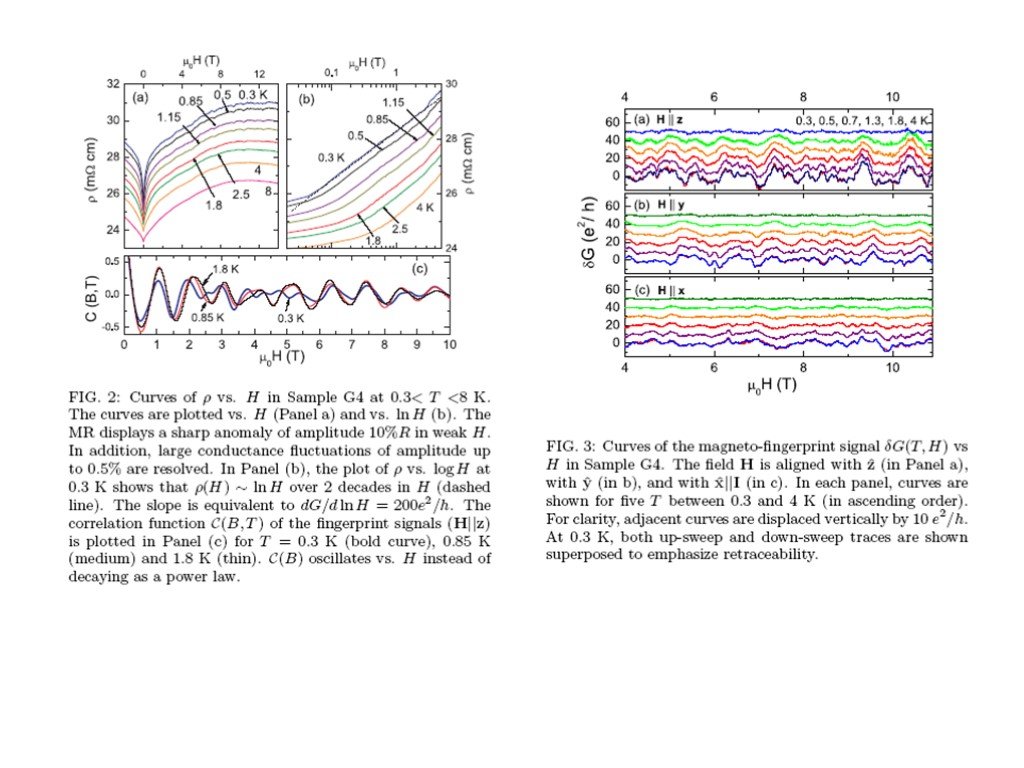
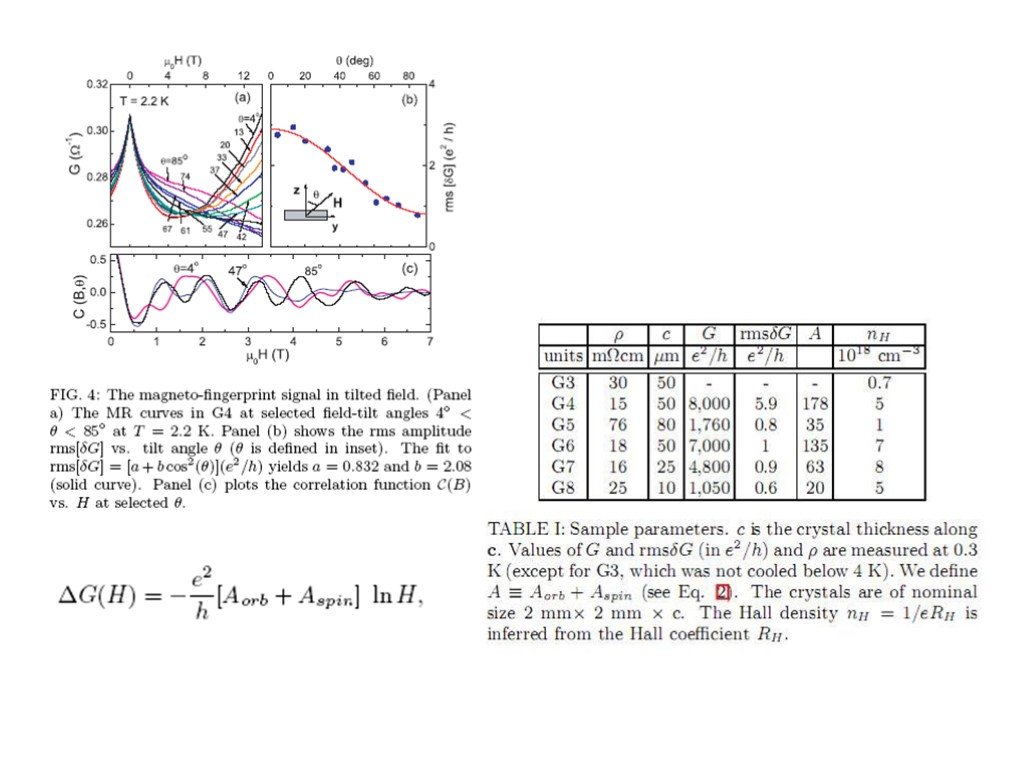
Giant magnetic fingerprint in non-metallic Bi2Se3 J.Checkelsky et al arXiv:0909.1840
Superconductivity in CuxBi2Se3 and its implications for pairing in the undoped topological insulator Y. S. Hor, A. J. Williams, J. G. Checkelsky, P. Roushan, J. Seo, Q. Xu, H. W. Zandbergen, A. Yazdani, N. P. Ong, R. J. Cava arXiv:0909.2890
Nonlocal transport in quantum spin-Hall state in HgTe quantum well
Слайд 27
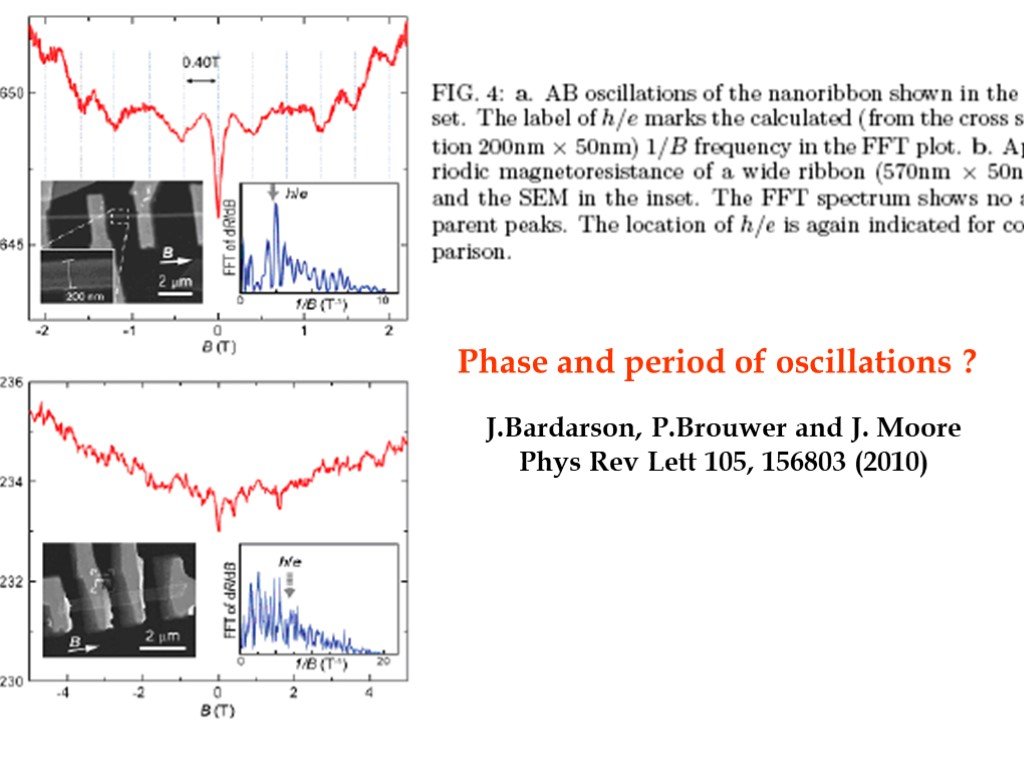
Слайд 28Phase and period of oscillations ?
J.Bardarson, P.Brouwer and J. Moore Phys Rev Lett 105, 156803 (2010)
Слайд 29
Слайд 30
Слайд 31
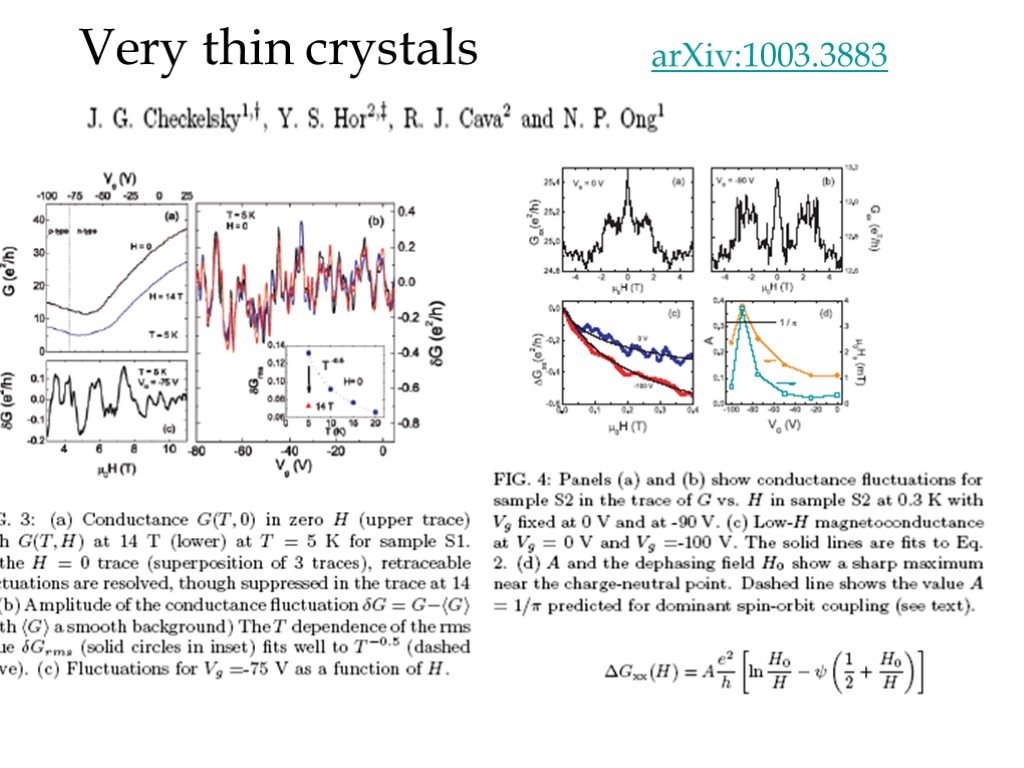
Слайд 32Very thin crystals arXiv:1003.3883
Слайд 33
Слайд 34Лекция 2. Теория
Топологические свойства зонных диэлектриков Общая классификация возможных топологических фаз в размерностях d=1,2,3 Связь с проблемами спиновой жидкости и px+ipy сверхпроводящего состояния Майорановские фермионы: как напасть на их след
Слайд 35Теория зонных ТИ
Общая топологическая классификация
Топологические калибровочные теории
Arxiv:1011.3485
Слайд 36Phys Rev B 76, 045302 (2007) 75, 195312 (2006)
2D:
Слайд 37
Слайд 38Непрерывный предел: 0< m +2 << 1
Слайд 39Dimensional reduction
приводит к сумме 1D членов
= integer
Слайд 40Магнитоэлектрический эффект в присутствии щели на пов-сти
Для бесщелевой поверхности выведено эффективное действие с дираковскими фермионами
Слайд 41Singe Dirac point on the sphere
Как это совместить с открытием щели в тонкой пластинке ?
Слайд 42Туннель для связи с антиподами
Тонкая бесконечная пластинка ТИ На верхней и нижней поверхностях живут дираковские электроны (как в графене, но нет 4-вырождения)
Yi Zhang, Ying Ran, Ashvin Vishwanath arxiv:0904.0690
Сквозной туннель радиуса R содержит на внутренней поверхности состояния со спектром
n = m + ½ - (Φ/Φ0) m – целое число
Слайд 43General classification: A.Kitaev, A.Ludwig et al
Слайд 44Connections to spin-liquids and p+ip superconductors
Основы: Недавние работы
Phys. Rev. B 79, 180501(R) (2009) Exactly solvable pairing model for superconductors with px+ipy-wave symmetry M. Ibañez, Jon Links, G. Sierra, and S.-Y. Zhao Gauge symmetry in Kitaev-type spin models and index theorems on odd manifolds Yue Yu arXiv:0704.3829 Nucl. Phys. B 799, 345 (2008)
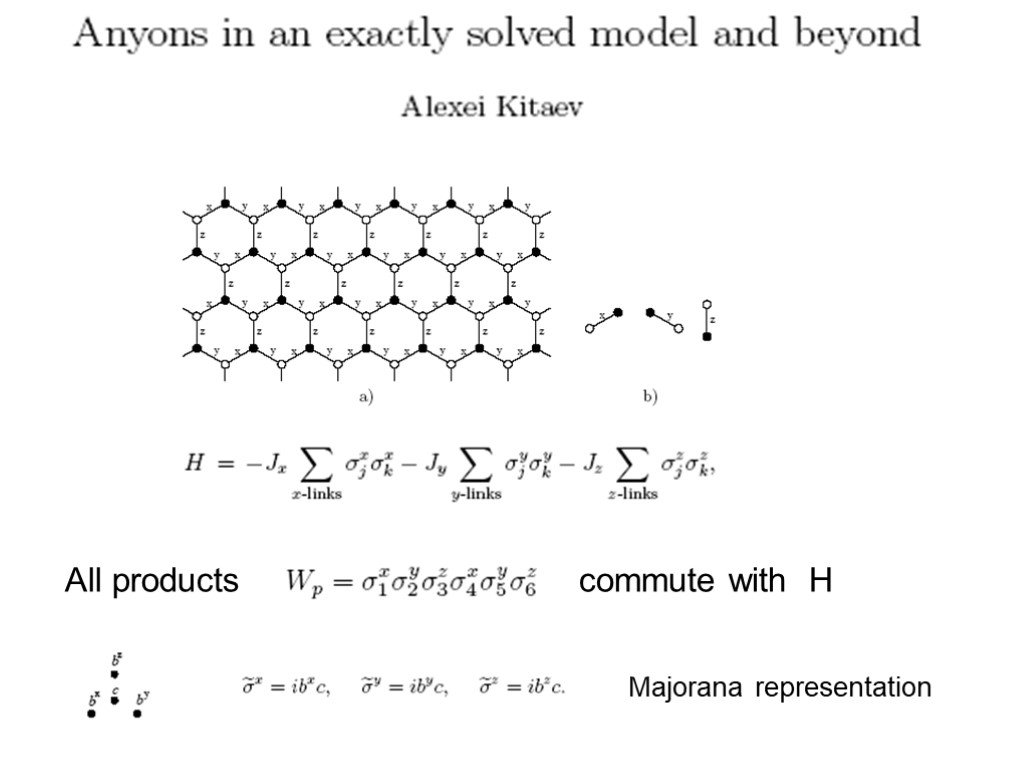
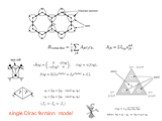
Слайд 45All products commute with H Majorana representation
Слайд 46single Dirac fermion mode!
Слайд 47B-phase can be made gapful
1) Including of magnetic field, or NNN fermionic couplings (Kitaev 2006)
2) Going to decorated honeycomb lattice (Yao-Kivelson 2007)
Chern number
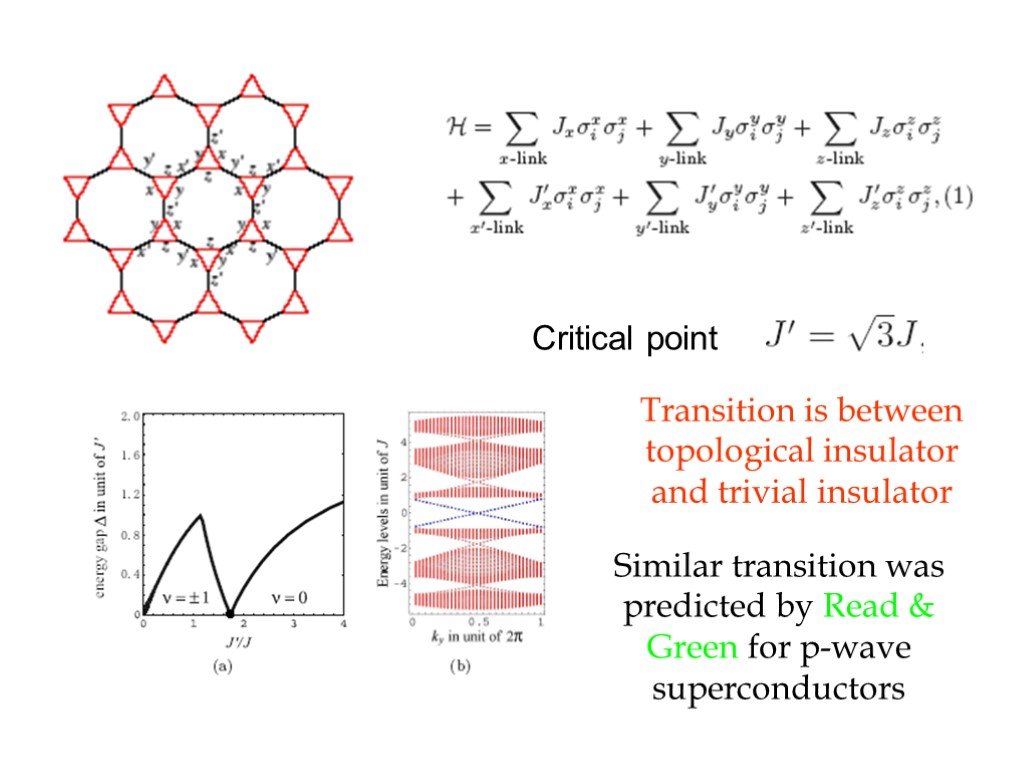
Слайд 48Critical point
Transition is between topological insulator and trivial insulator
Similar transition was predicted by Read & Green for p-wave superconductors
Слайд 49Майорановские состояния в центрах сверхпроводящих вихрей и неабелева обменная статистика
D.A.Ivanov PRL 2001 4 vortices: Non-Ab trans.
Слайд 50Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator Phys. Rev. Lett. 100, 096407 (2008) L. Fu and C. L. Kane
Bi2Se3 Nb Chiral states
Слайд 51Аналогия (неполная) с px+ipy сверхпроводником
H = Time-reversal operator original fermions chiral fermions
Due to phase factors the current Hamiltonian (1) is T-inv. whereas px+ipy superconductor breaks T-invariance
(1)
Слайд 52Сверхпроводящий эффект близости на поверхности ТИ
С учетом примесного рассеяния на поверхности, которое не должно приводить к распариванию (из-за того, что T-инвариантность не нарушена)
Зависимость Ic(L,T) - способ измерить коэфф. диффузии поверхностных состояний
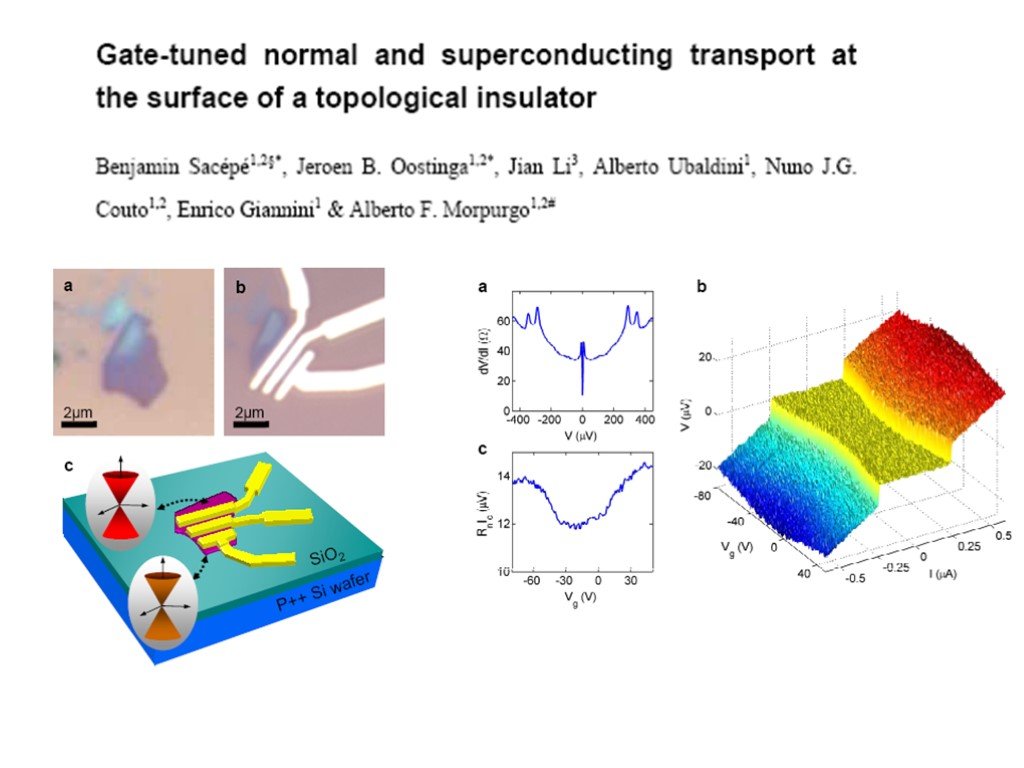
Эксперимент B.Sacepe et al – джозеф. ток на поверхности

Слайд 53Индуцированная сверхпроводимость и майорановские состояния
Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator Phys. Rev. Lett. 100, 096407 (2008) L. Fu and C. L. Kane Они же: arXiv:0804.4469, arXiv:0903.2427 Phys. Rev. Lett. 102, 216404 (2009) Electrically Detected Interferometry of Majorana Fermions in a Topological Insulator A. R. Akhmerov, Johan Nilsson, and C. W. J. Beenakker Manipulation of Majorana fermion, Andreev reflection and Josephson current on topological insulators Yukio Tanaka, Takehito Yokoyama, Naoto Nagaosa arXiv:0907.2088 Majorana Fermion Induced Resonant Andreev Reflection K. T. Law, Patrick A. Lee, T. K. Ng arXiv:0907.1909 Detecting Majorana bound states induced by a topological insulator Colin Benjamin, Jiannis K. Pachos arXiv:0908.0655
Слайд 54
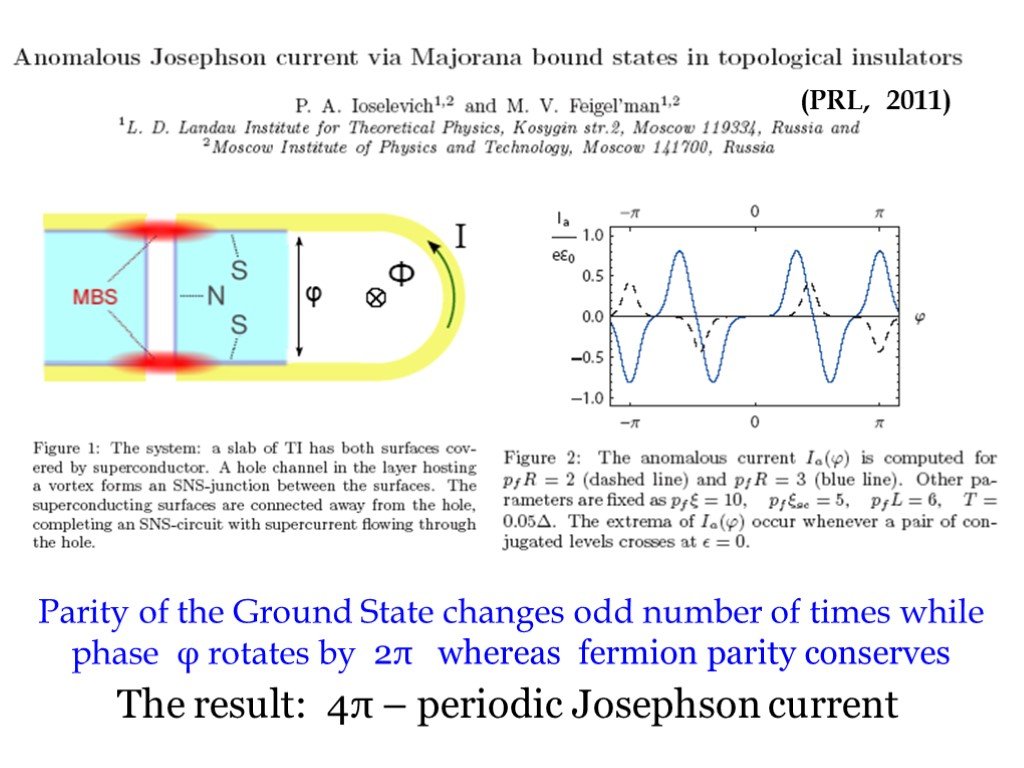
Слайд 55(PRL, 2011)
Parity of the Ground State changes odd number of times while phase φ rotates by 2π whereas fermion parity conserves
The result: 4π – periodic Josephson current