Презентация "Лобачевский Николай Иванович" (10 класс) по истории – проект, доклад

Презентация на тему:»Лобачевский Николай Иванович и его творческий путь.»

План: 1-ознакомление с Николаем Лобачевским. 2-биография Николая Ивановича. 3-труды,профессиональные должности,значимые работы. 4-понятие «геометрии Лобачевского». 5-разбор задачи о параллельных прямых. 6-награды Лобачевского.

Лобачевский Николай Иванович (1792 - 1856)

Николай Иванович Лобачевский (20 ноября (1 декабря) 1792, Нижний Новгород — 12 (24) февраля 1856, Казань) — русский математик, создатель неевклидовой геометрии, названной его именем, деятель университетского образования и народного просвещения. Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии». Лобачевский в течение 40 лет преподавал в Казанском университете, в том числе 19 лет руководил им в должности ректора; его активность и умелое руководство вывели университет в число передовых российских учебных заведений.

Лобачевский Николай Иванович

Николай Иванович Лобачевский родился 1 декабря (20 ноября) 1792 года в Нижнем Новгороде в бедной семье мелкого чиновника. Отец Лобачевского умер, когда сыну исполнилось 7 лет. Осталась Прасковья Александровна Лобачевская с тремя малолетними сыновьями без средств. Она вместе с детьми переезжает в Казань. Её стараниями девятилетний мальчик был устроен вместе с двумя братьями в гимназию на казенное содержание.

Лобачевский закончил гимназию в конце 1806 года, показав хорошие знания, особенно по математике и языкам — латинскому, немецкому, французскому. В проявившемся уже тогда его интересе к математике — большая заслуга преподавателя гимназии Г. И. Карташевского.

В январе 1807 года 14-летний Лобачевский вместе с младшим братом поступил в основанный в 1804 году Казанский Императорский университет, которому отдал 40 лет жизни. В рапорте о поведении Лобачевского отмечаются: упрямство, «мечтательное о себе самомнение, упорство, неповиновение», а также «возмутительные поступки» и даже «признаки безбожия». Над ним нависла угроза отчисления и отдачи в солдаты, но заступничество Бартельса и ещё одного преподавателя, Франца Броннера, помогло отвести опасность.

В 1811 году, окончив университет, Лобачевский получил степень магистра по физике и математике с отличием и был оставлен при университете; перед этим его заставили покаяться за «дурное поведение» и дать обещание впредь вести себя примерно. В 1814 году 21-летний Лобачевский был утверждён адъюнктом, то есть, по современной терминологии, доцентом.

С этого времени его жизнь и работа протекают в Казани. 28-летнего Лобачевского, уже успевшего показать незаурядные организаторские способности, назначили вместо Бартельса деканом физико-математического факультета. Круг его обязанностей был обширен — чтение лекций по математике, астрономии и физике, комплектация и приведение в порядок библиотеки, музея, физического кабинета, создание обсерватории и т. д. В списке служебных обязанностей есть даже «наблюдение за благонадёжностью» всех учащихся Казани. В эти годы Лобачевский подготовил учебник по геометрии, осуждённый рецензентом (академиком Фуссом) за использование метрической системы мер и чрезмерный отход от Евклидовского канона (он так и не был опубликован при жизни автора). Другой написанный им учебник, по алгебре, удалось опубликовать только спустя 10 лет (1834). 3 мая 1827 года 35-летний Лобачевский тайным голосованием был избран ректором университета (11 голосами против 3).

Новый ректор, со свойственной ему энергией, сразу погрузился в хозяйственные дела — реорганизация штата, строительство учебных корпусов, механических мастерских, лабораторий и обсерватории, поддержание библиотеки и минералогической коллекции, участвует в издании «Казанского Вестника» и т. п. Многое делал собственными руками. За время работы в университете он вёл курсы по геометрии, тригонометрии, алгебре, анализу, теории вероятностей, механике, физике, астрономии и даже гидравлике, часто замещал отсутствующих преподавателей. Одновременно с преподаванием Лобачевский читал лекции для населения. И одновременно он неустанно развивал и шлифовал главное дело своей жизни — неевкли научно-популярные дову геометрию. Первый набросок новой теории — доклад «Сжатое изложение начал геометрии» Лобачевский сделал 11 (23) февраля 1826 года, дата этого выступления считается днём рождения неевклидовой геометрии. В 1832 году Лобачевский женился на Варваре Алексеевне Моисеевой, которая была почти на 20 лет моложе его. Точное количество родившихся детей неизвестно. Согласно послужному списку, выжили семь детей

В 1832—1834 гг. опубликованный труд Лобачевского по неевклидовой геометрии подвергается резкой невежественной критике в Петербурге (подробнее см. ниже). Его служебный авторитет пошатнулся, на третий срок (1833) Лобачевский избран ректором всего 9 голосами против 7. В 1834 году по инициативе Лобачевского вместо «Казанского вестника» начинается издание «Учёных записок Казанского университета», где, бросая вызов своим противникам, он публикует свои новые открытия. Петербургские профессора оценивали научные труды Лобачевского неизменно отрицательно, ему так и не удалось защитить диссертацию.

Материальные лишения он переносил стойко, но однажды ради денежного пари (для приобретения учебников) решился на озорство, за которое его чуть-чуть не разжаловали из студентов в солдаты: сидя на корове, он проскакал по университетскому парку.

В 1836 году университет посетил царь Николай I, остался доволен и наградил Лобачевского престижным орденом Анны II степени, дававшим право на потомственное дворянство.

29 апреля 1838 года «за заслуги на службе и в науке» Н. И. Лобачевскому было пожаловано дворянство и дан герб: Щит разделен на две части, из коих в верхней в красном поле изображены шестиугольная из двух золотых треугольников составленная звезда и летящая вверх пчела, а в нижней в голубом поле стрела и серебряная подкова, шипами вверх обращенная. Щит увенчан дворянским шлемом и короной с тремя на одной страусовыми перьями. Намёт на щите голубой, подложенный золотом. Герб Лобачевского внесен в Часть 11 Общего гербовника дворянских родов Всероссийской империи.

Лобачевский был ректором Казанского университета в период с 1827 по 1846 годы, пережив эпидемию холеры (1830) и сильнейший пожар (1842), уничтоживший половину Казани. Благодаря энергии и умелым действиям ректора жертвы и потери в обоих случаях были минимальны. Усилиями Лобачевского Казанский университет становится первоклассным, авторитетным и хорошо оснащённым учебным заведением, одним из лучших в России.

Вскоре Лобачевский разорился, дом в Казани и имение жены были проданы за долги. В 1852 году умер старший сын Алексей, любимец Лобачевского. Здоровье его самого было подорвано, слабеет зрение. Последний труд учёного, «Пангеометрия», записали под диктовку ученики слепого учёного в 1855 году. Скончался 12 (24) февраля 1856 года, в тот самый день, в который 30 годами ранее впервые обнародовал свою версию неевклидовой геометрии. Похоронен на Арском кладбище Казани.

Конец 1830-х годов был печален для Лобачевского. Умерла дочь Надежда, скончались Бартельс и Карташевский, а 27 февраля 1840 года в его доме умерла мать Прасковья Александровна.

Геометрия Лобачевского.

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, являются общими для обеих геометрий; они образуют так называемую абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрии. Приведём (в современных обозначениях) несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским.

Через точку P, не лежащую на данной прямой R (см. рисунок), проходит бесконечно много прямых, не пересекающих R и находящихся с ней в одной плоскости; среди них есть две крайние x, y, которые и называются параллельными прямой R в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) R общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек). Угол θ между перпендикуляром PB из P на R и каждой из параллельных (называемый углом параллельности) по мере удаления точки P от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель x с одной стороны (а y с противоположной) асимптотически приближается к а, а с другой — бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден). Для точки, находящейся от заданной прямой на расстоянии PB = a Лобачевский дал формулу для угла параллельности П(a).

Здесь q — некоторая постоянная, связанная с кривизной пространства Лобачевского. Она может служить абсолютной единицей длины аналогично тому, как в сферической геометрии особое положение занимает радиус сферы.

Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой. В геометрии Лобачевского не существует подобных, но неравных треугольников; треугольники равны, если их углы равны. Сумма углов всякого треугольника меньше π и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность δ = π − (α + β + γ), где α, β, γ — углы треугольника, пропорциональна его площади:

Из формулы видно, что существует максимальная площадь треугольника, и это конечное число: πq2. Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом. Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом. Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии. Длина окружности не пропорциональна радиусу, а растёт быстрее. В частности, в геометрии Лобачевского число π не может быть определено как отношение длины окружности к её диаметру. Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от π; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2π, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского.

Итак, допустим, что пятый постулат не верен: через точку А, не принадлежащую прямой b, можно провести более чем одну прямую, которая не пересекается с прямой b.(рис1)

Аксиомы евклидовой геометрии являются продуктом повседневных наблюдений человека, кроме одной – аксиомы о параллельных прямых, называемой также пятым постулатом: «Через точку вне прямой можно провести в их плоскости только одну прямую, не пересекающую данной.»

Пусть прямые а' и а" не пересекаются с в. При их расположении, как на рисунке, будем поворачивать прямую а' по часовой стрелке. Тогда найдется прямая с', которая "в последний раз" не пересекается с b. Значит, прямые, получающиеся из с' при повороте по часовой стрелке (на сколь угодно малый угол), будут пересекать прямую b, а прямые, получающиеся из с при малом повороте в обратном направлении, не будут пересекать b.

Иначе говоря, среди всех прямых, проходящих через точку А, прямая с' отделяет пересекающие в прямые от непересекающих ее. Сама прямая с' не пересекает b. Такая же картина наблюдается и для прямой с", симметричной с' относительно перпендикуляра АР, опущенного на в. Она отделяет пересекающие в прямые от не пересекающих. Лобачевский называет прямые с' и с" параллельными прямой b, причем с' параллельна вправо. Остальные прямые, проходящие через точку А и не пересекающие прямую b (такие, как а" и а'), именуются расходящимися с прямой b. Далее, обозначим длину отрезка АР через х, а острый угол, образуемый прямой с' или с" с прямой АР, - через П(х).

Лобачевский вводит эти определения и обозначения, стремясь, со свойственной ему настойчивостью, узнать, что может получиться из его предположения о неверности пятого постулата, и быстрее обнаружить желанное противоречие. На наших чертежах линии изогнуты. Но вы должны понять, что Лобачевский рассуждает именно о прямых линиях. Если отрезок АР мал, то острый угол П(х) близок к 90°. Когда отрезок АР совсем мал, то, посмотрев "в микроскоп" на точку Р (рис.), мы увидим, что прямые с' и с" практически сливаются, поскольку угол П(х) очень близок к 90 градусам.

В целом же, в силу предположения о неверности пятого постулата, приходится изображать линии изогнутыми. И если в дальнейшем будут появляться все более и более странные вещи, то это только хорошо - мы скорее наткнемся на долгожданное противоречие. Лобачевский доказывает (все в том же предположении неверности пятого постулата), что две параллельные прямые неограниченно сближаются друг с другом в сторону параллельности, но в обратном направлении они неограниченно удаляются друг от друга.

А две расходящиеся прямые имеют единственный общий перпендикуляр, по обе стороны от которого они неограниченно удаляются друг от друга. Это очень похоже на то, о чем писал Лежандр, но мы уже знаем, что здесь пока ещё нет никакого противоречия. Затем Лобачевский рассматривает две параллельные прямые b и с и берет на прямой b движущуюся точку М, удаляющуюся в сторону, обратную параллельности.

В каждом положении точки М он восставляет перпендикуляр р к прямой b до его пересечения с прямой с. Длина перпендикуляра непрерывно возрастает при движении точки М, и, когда она попадает в некоторое положение Q, длина перпендикуляра становится бесконечной. Точнее говоря, перпендикуляр р, восстановленный к прямой b в точке Q, параллелен прямой с.

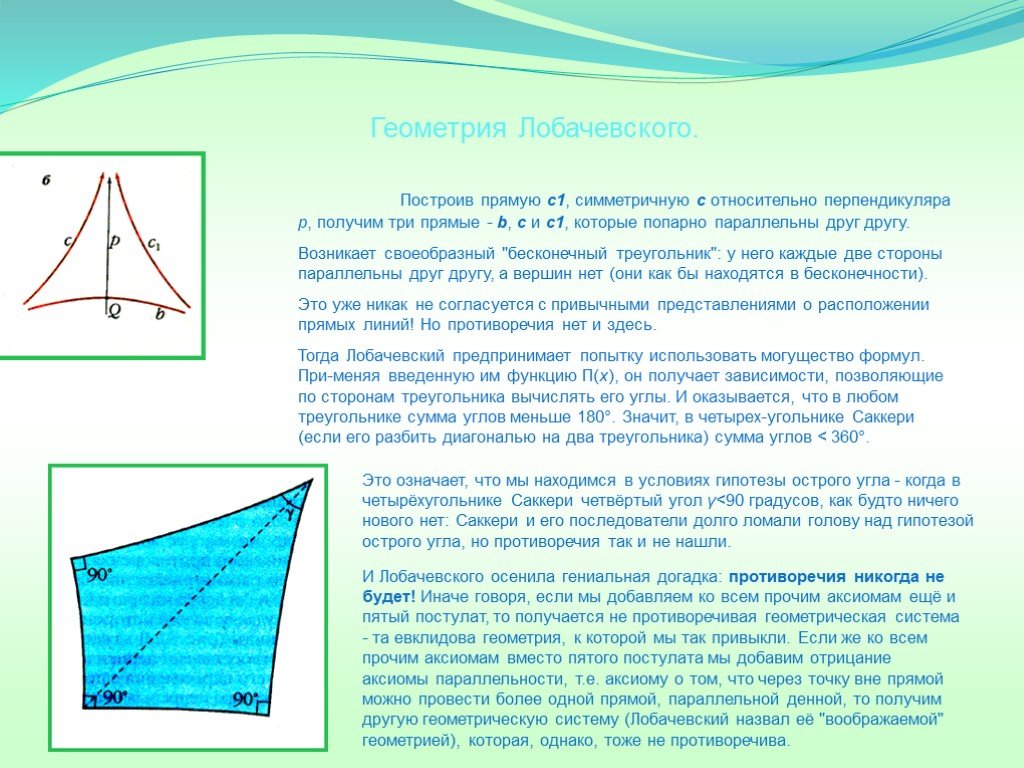
Построив прямую с1, симметричную с относительно перпендикуляра р, получим три прямые - b, с и с1, которые попарно параллельны друг другу. Возникает своеобразный "бесконечный треугольник": у него каждые две стороны параллельны друг другу, а вершин нет (они как бы находятся в бесконечности). Это уже никак не согласуется с привычными представлениями о расположении прямых линий! Но противоречия нет и здесь. Тогда Лобачевский предпринимает попытку использовать могущество формул. При-меняя введенную им функцию П(х), он получает зависимости, позволяющие по сторонам треугольника вычислять его углы. И оказывается, что в любом треугольнике сумма углов меньше 180°. Значит, в четырех-угольнике Саккери (если его разбить диагональю на два треугольника) сумма углов

Это означает, что мы находимся в условиях гипотезы острого угла - когда в четырёхугольнике Саккери четвёртый угол γ

И Лобачевского осенила гениальная догадка: противоречия никогда не будет! Иначе говоря, если мы добавляем ко всем прочим аксиомам ещё и пятый постулат, то получается не противоречивая геометрическая система - та евклидова геометрия, к которой мы так привыкли. Если же ко всем прочим аксиомам вместо пятого постулата мы добавим отрицание аксиомы параллельности, т.е. аксиому о том, что через точку вне прямой можно провести более одной прямой, параллельной денной, то получим другую геометрическую систему (Лобачевский назвал её "воображаемой" геометрией), которая, однако, тоже не противоречива.

Награды и увековечение памяти.

В течение жизни Н. И. Лобачевский получил за неутомимую и плодотворную служебную деятельность несколько наград: 1819: как профессор получил чин надворного советника. 1824: орден Святого Владимира IV степени, чин коллежского советника. 1831: личная благодарность царя за успешную борьбу с эпидемией холеры и перстень с бриллиантом. Царский подарок Лобачевский был вынужден в годы нужды продать[20]. 1833: орден Святого Станислава III степени, чин статского советника. 1836: орден Святой Анны II степени с короной и бриллиантами, звание потомственного дворянина (утверждено в 1838 году). 1838: чин действительного статского советника[21]. 1841: звание заслуженного профессора по выслуге 25 лет. 1842: по рекомендации Гаусса избран членом-корреспондентом Гёттингенского королевского научного общества. 1844: орден Святого Станислава I степени. 1855: по случаю столетия Московского университета избран его почётным членом, с вручением серебряной медали. В 1892 году в России и в других странах широко отметили 100-летний юбилей Лобачевского. Была учреждена международная премия имени Н. И. Лобачевского (1895)[22], в Казани открыт памятник учёному (скульптор М. Л. Диллон, архитектор Игнатьев) (1896). 200-летие Лобачевского отмечалось в 1992 году. Банком России была выпущена памятная монета в серии «Выдающиеся личности России».

Завершение презентации.

В завершении нашей работы,мне хотелось бы сказать,что данной презентацией я хотел показать,какой вклад сделал Лобачевский в развитие геометрии,через одного человека я попытался показать всю сущность,красоту,общность геометрических познаний,на которые способен каждый человек.

Web-ресурсы.

Материалы для презентации были взяты со следующих ссылок: http://ru.wikipedia.org/wiki/ http://www.rulex.ru/01120306.htm http://www.calend.ru/person/399/